函数的极值与导数

课件18张PPT。 函数的极值与导数 已知函数 f(x)=2x3-6x2+7
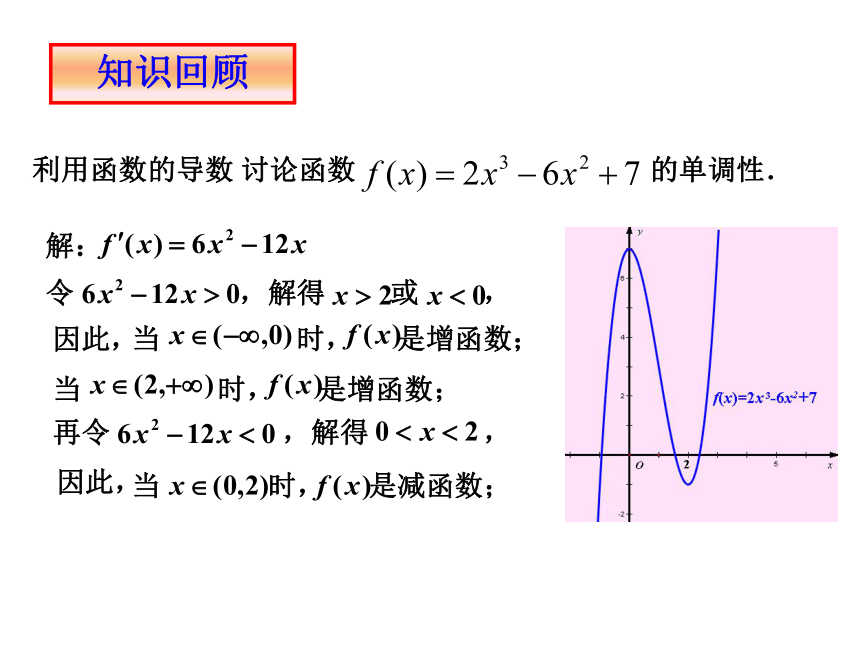
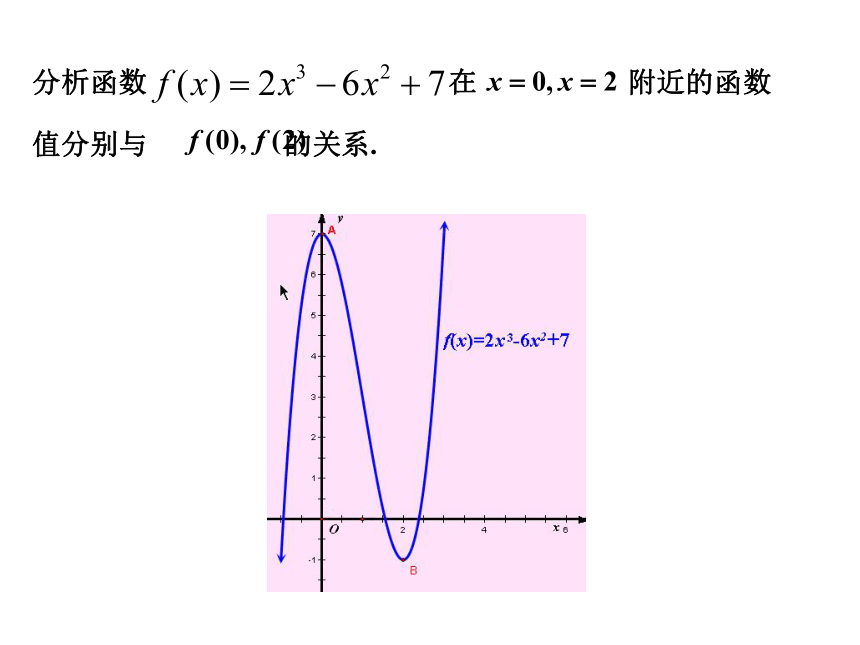
(1)求f(x)的单调区间,并画出其图象;【复习与思考】(2)函数f(x)在x=0和x=2处的函数值与这两点附近的函数值有什么关系?知识回顾利用函数的导数 讨论函数 的单调性．解：分析函数 在 附近的函数值分别与 的关系. 设函数y=f(x)在x=x0及其附近有定义，
(1)如果在x=x0处的函数值比它附近所有各点的函数值都大，即f(x)y=f(x)的一个极大值.记作:y极大值=f(x0)【函数极值的定义】(2)如果在x=x0处的函数值比它附近所有各点的函数值都小，即f(x)>f(x0),则称 f(x0)是函数
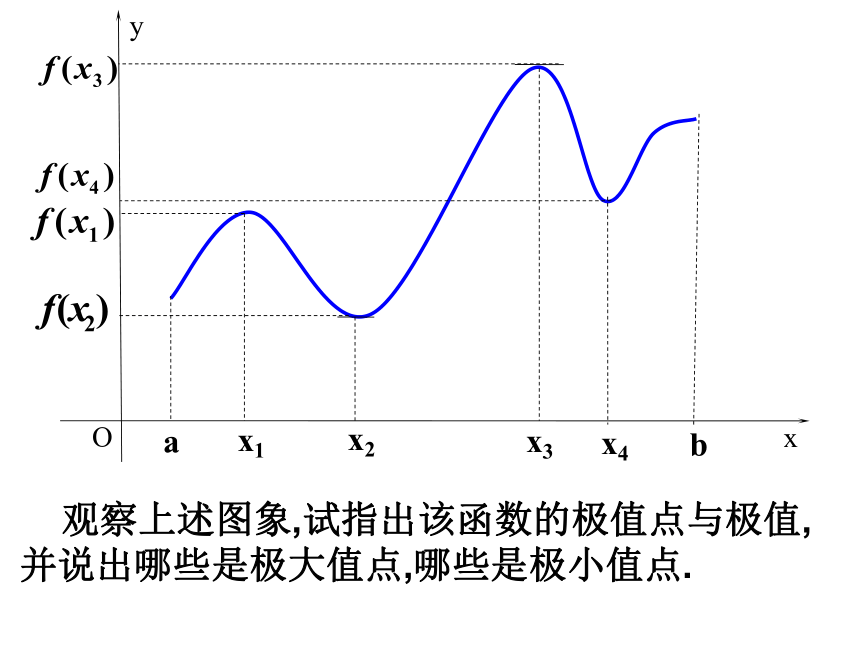
y=f(x)的一个极小值.记作:y极小值=f(x0)极大值与极小值统称为极值,x0叫做函数的极值点. 观察上述图象,试指出该函数的极值点与极值,并说出哪些是极大值点,哪些是极小值点.(1)极值是一个局部概念,反映了函数在某一点附近的大小情况;(2)极值点是自变量的值，极值指的是函数值;(3)函数的极大(小)值可能不止一个,而且函数的极大值未必大于极小值;【关于极值概念的几点说明】(4)函数的极值点一定在区间的内部，区间的端点不能成为极值点。而函数的最值既可能在区间的内部取得，也可能在区间的端点取得。【问题探究】 函数y=f(x)在极值点的导数值为多少?在极值点附近的导数符号有什么规律? 一般地，当函数 在点 处连续时，判断 是极大（小）值的方法是：
f’(x0)=0 （1）如果在 附近的左侧 ，右侧 ，那
么 是极大值． （2）如果在 附近的左侧 ，右侧 ，那
么 是极小值．注：导数为0的点不一定是极值点．观察与思考：极值与导数有何关系？对于可导函数,
若x0是极值点,则 f’(x0)=0;
反之,若f’(x0)=0,则x0不一定是极值点.函数y=f(x)在一点的导数为0是函数在这点取极值的必要条件，
而非充分条件。函数y=f(x)在x0取极值的充分条件是:
（1）f’(x0)=0
(2)在x0附近的左侧 f’(x0)>0(<0)，右侧f’(x0)<0(>0)（1） 求导数f/(x)；
（2） 解方程 f/(x)=0
（3） 通过列表检查f/(x)在方程f/(x)=0的根的左右两侧的符号，进而确定函数的极值点与极值.【求函数极值的步骤】例、求函数 的极值． 例题讲解解：当 时，y有极大值，并且当 时，y有极小值，并且例、求函数 的极值． 解：当 时，y有极小值，并且注意：函数极值是在某一点附近的小区间内定义的，是局部性质。因此一个函数在其整个定义区间上可能有多个极大值或极小值，并对同一个函数来说，在某一点的极大值也可能小于另一点的极小值。练习1.判断下面4个命题，其中是真命题序号为 。
①可导函数必有极值；
②可导函数在极值点的导数一定等于零；
③函数的极小值一定小于极大值
（设极小值、极大值都存在）；
④函数的极小值（或极大值）不会多于一个。②2、函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习： 函数 在 时有极值10，则a，b的值为（ ）
A、 或
B、 或
C、 D、 以上都不对 C，注意：f/(x0)=0是函数取得极值的必要不充分条件注意代入检验 3..略解：(1)由图像可知：(2)注意：数形结合以及函数与方程思想的应用