10.1相交线(1)
图片预览

文档简介
课题 10.1 相交线(1)
教学目标
知识与技能:理解并掌握对顶角的概念;理解对顶角的性质。了解垂直的定义。
过程与方法:通过动手、操作、推断、交流等活动,进一步发展空间观念,培养识图能力、推理能力和表达能力;在具体情境中了解对顶角、邻补角,能找出图形中的一个角的对顶角,理解对顶角相等的性质,并能运用其解决一些简单问题;经历一般到特殊的数学过程,理解垂直是相交的一种特例。
情感、态度与价值观:引导学生对图形观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中,获取成功的体验,树立学习的信心。
重点与难点
理解与掌握对顶角的概念和性质是本节课的重点;对顶角性质的探索及运用对顶角相等和两直线垂直解决一些实际问题时本节课的难点。
教具准备
多媒体课件、三角板
教学过程
1、 创设情境、导入新课
课件展示图片,让学生观察、感受生活中的平行线与相交线。
让学生举出生活中相交线的实例。
让学生结合实例(剪刀)根据已学知识画出两条直线相交的图形,并标注字母,用几何语言表述。
2、 交流合作、探索新知
观察并讨论:
1、两条直线相交组成几个小于平角的角?
2、这些角中每两个角有怎样的位置关系?
3、试根据它们的位置关系将这些角进行分类。
4、猜想并验证∠1、 ∠2 、∠3 、∠4两两之间有什么数量关系?(度量、折叠、推理)
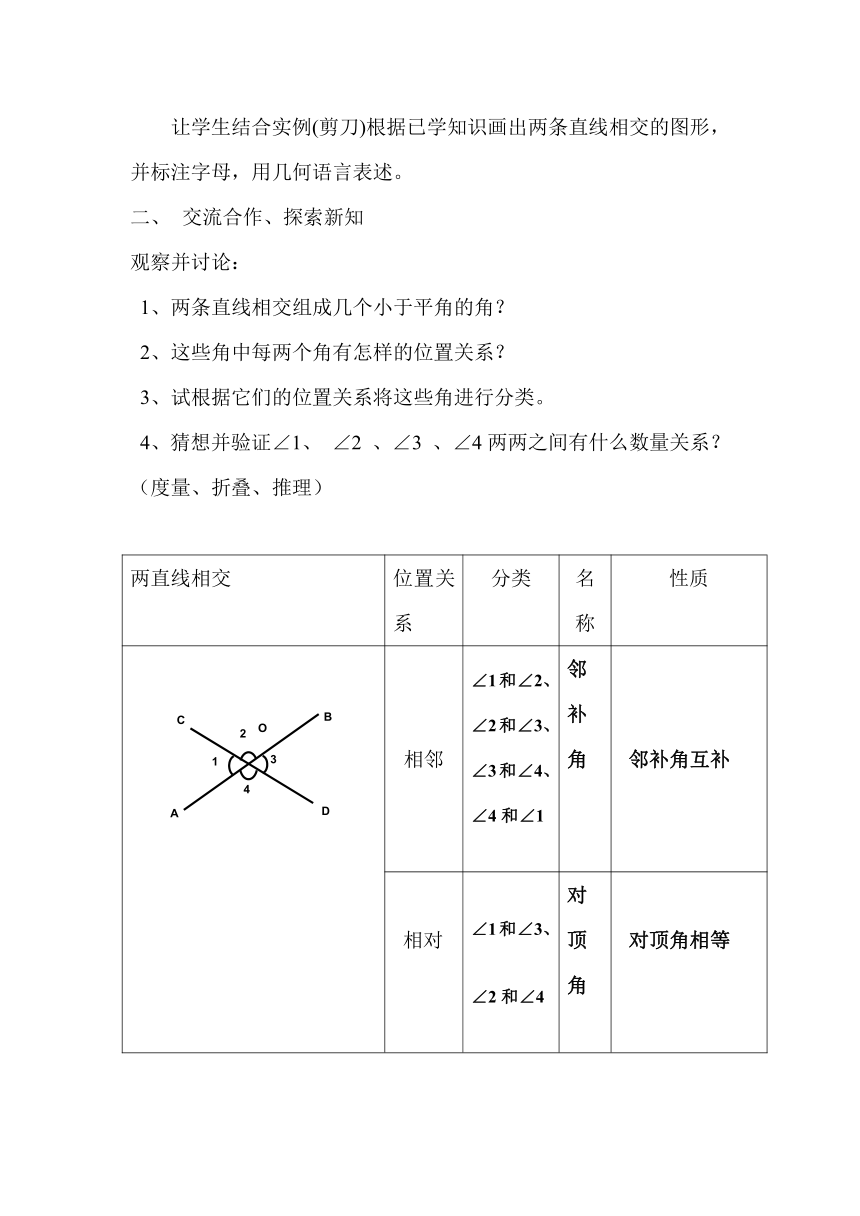
两直线相交 位置关系 分类 名称 性质
相邻 ∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1 邻补角 邻补角互补
相对 ∠1和∠3、∠2和∠4 对顶角 对顶角相等
3、 应用新知、巩固练习
练习一:
1、下列图中,∠1与∠2是对顶角吗?为什么?
2、如图1,三条直线AB、CD、EF两两相交,在这个图形中有
对顶角_____对.
3、如图2,直线AB、CD
相交于O,OE是射线。则
∠1的对顶角是_____________,
∠3的对顶角是_____________,
练习二:
1、若∠1与∠2是对顶角,∠1=16°,则∠2=______°;
若 ∠3与∠4是邻补角,则∠3+∠4 =______°.
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= _
3、图中是对顶角量角器,你能说出用它测量角的原理吗?
例题解析
例1:如图,直线a、b相交, ∠ 1=40°, 求∠2,∠3 ,∠4的度数。
解:由∠1和∠2互补,得
∠2=180°-∠1
=180°- 40°
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
变式 已知直线a、b相交,∠1=90°,求∠2,∠3 ,∠4的度数。
你能画出图形吗?
结论 已知两条直线相交成的四个角,其中一个角是90°,其余各角都是_____ 。
四、新知拓展
定义 两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线相互垂直。其中一条直线叫做另一条直线的垂线,他们的交点O叫做垂足。
表示方法 直线AB和CD相互垂直,记作“AB⊥CD”,
读作“AB垂直于CD”。
如图:∠AOC=90° AB⊥CD
五、知识回顾、课堂小结
六、课外思考、拓展提高
2、两条直线相交于一点,有几对对顶角?
三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角?
n 条直线相交于一点,有几对对顶角?
七、布置作业
作业:P118 习题10.1 第1、2、3题。
4
3
2
1
O
D
C
A
B
你能再举出一些生活中有关垂直的实例吗?
你能再举出一些生活中有关垂直的实例吗?
O
D
C
A
图2
图1
B
教学目标
知识与技能:理解并掌握对顶角的概念;理解对顶角的性质。了解垂直的定义。
过程与方法:通过动手、操作、推断、交流等活动,进一步发展空间观念,培养识图能力、推理能力和表达能力;在具体情境中了解对顶角、邻补角,能找出图形中的一个角的对顶角,理解对顶角相等的性质,并能运用其解决一些简单问题;经历一般到特殊的数学过程,理解垂直是相交的一种特例。
情感、态度与价值观:引导学生对图形观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中,获取成功的体验,树立学习的信心。
重点与难点
理解与掌握对顶角的概念和性质是本节课的重点;对顶角性质的探索及运用对顶角相等和两直线垂直解决一些实际问题时本节课的难点。
教具准备
多媒体课件、三角板
教学过程
1、 创设情境、导入新课
课件展示图片,让学生观察、感受生活中的平行线与相交线。
让学生举出生活中相交线的实例。
让学生结合实例(剪刀)根据已学知识画出两条直线相交的图形,并标注字母,用几何语言表述。
2、 交流合作、探索新知
观察并讨论:
1、两条直线相交组成几个小于平角的角?
2、这些角中每两个角有怎样的位置关系?
3、试根据它们的位置关系将这些角进行分类。
4、猜想并验证∠1、 ∠2 、∠3 、∠4两两之间有什么数量关系?(度量、折叠、推理)
两直线相交 位置关系 分类 名称 性质
相邻 ∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1 邻补角 邻补角互补
相对 ∠1和∠3、∠2和∠4 对顶角 对顶角相等
3、 应用新知、巩固练习
练习一:
1、下列图中,∠1与∠2是对顶角吗?为什么?
2、如图1,三条直线AB、CD、EF两两相交,在这个图形中有
对顶角_____对.
3、如图2,直线AB、CD
相交于O,OE是射线。则
∠1的对顶角是_____________,
∠3的对顶角是_____________,
练习二:
1、若∠1与∠2是对顶角,∠1=16°,则∠2=______°;
若 ∠3与∠4是邻补角,则∠3+∠4 =______°.
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= _
3、图中是对顶角量角器,你能说出用它测量角的原理吗?
例题解析
例1:如图,直线a、b相交, ∠ 1=40°, 求∠2,∠3 ,∠4的度数。
解:由∠1和∠2互补,得
∠2=180°-∠1
=180°- 40°
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
变式 已知直线a、b相交,∠1=90°,求∠2,∠3 ,∠4的度数。
你能画出图形吗?
结论 已知两条直线相交成的四个角,其中一个角是90°,其余各角都是_____ 。
四、新知拓展
定义 两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线相互垂直。其中一条直线叫做另一条直线的垂线,他们的交点O叫做垂足。
表示方法 直线AB和CD相互垂直,记作“AB⊥CD”,
读作“AB垂直于CD”。
如图:∠AOC=90° AB⊥CD
五、知识回顾、课堂小结
六、课外思考、拓展提高
2、两条直线相交于一点,有几对对顶角?
三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角?
n 条直线相交于一点,有几对对顶角?
七、布置作业
作业:P118 习题10.1 第1、2、3题。
4
3
2
1
O
D
C
A
B
你能再举出一些生活中有关垂直的实例吗?
你能再举出一些生活中有关垂直的实例吗?
O
D
C
A
图2
图1
B
