沪科版九年级数学下册24.2.3圆心角、弧、弦、弦心距之间的关系测试卷(解析版)
文档属性
| 名称 | 沪科版九年级数学下册24.2.3圆心角、弧、弦、弦心距之间的关系测试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 343.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-04 22:45:46 | ||
图片预览



文档简介
沪科版九年级数学下册24.2.3
《圆心角、弧、弦、弦心距之间的关系》
测试卷
一.选择题(共10小题)
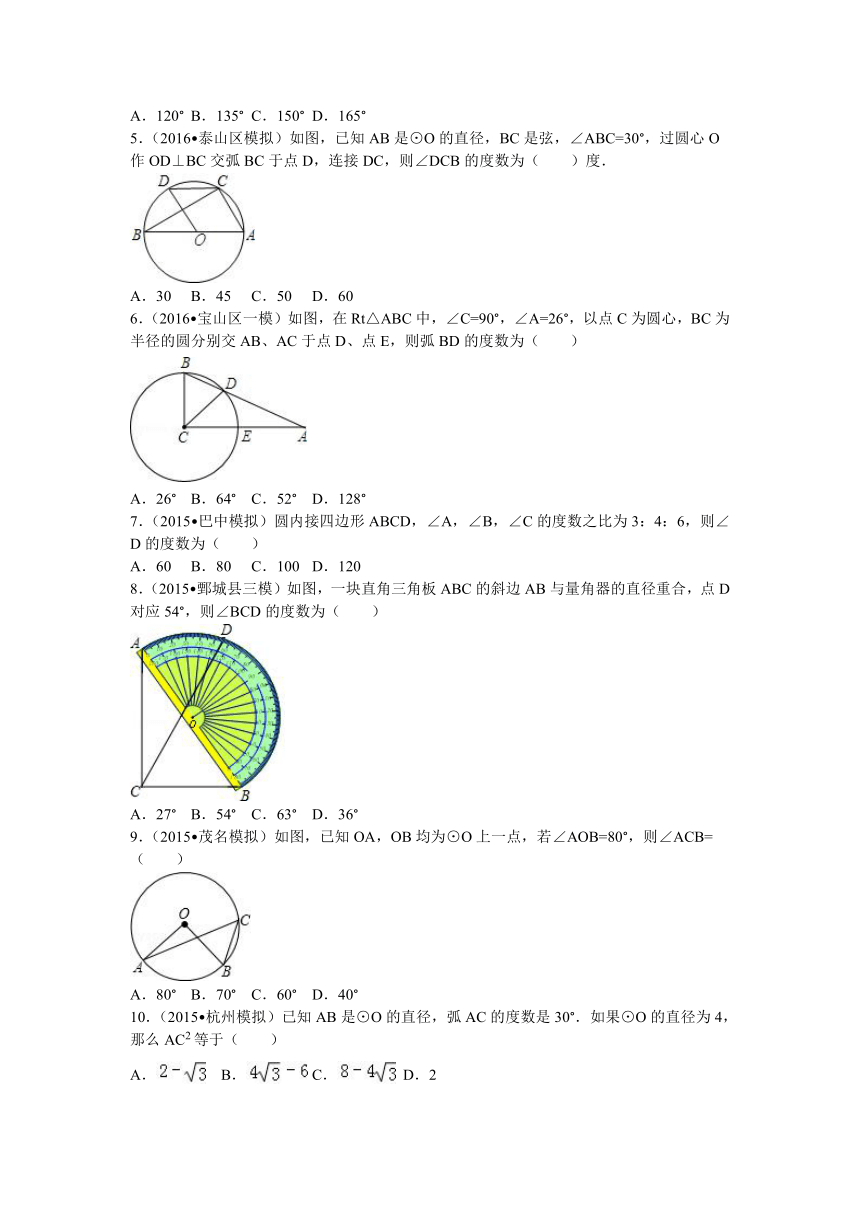
1.(2016 兰州)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )
A.40°
B.45°
C.50°
D.60°
2.(2016 济宁)如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40°
B.30°
C.20°
D.15°
3.(2016 台湾)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=65°,∠D=60°,则的度数为何?( )
A.25
B.40
C.50
D.55
4.(2016 舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120°
B.135°
C.150°
D.165°
5.(2016 泰山区模拟)如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A.30
B.45
C.50
D.60
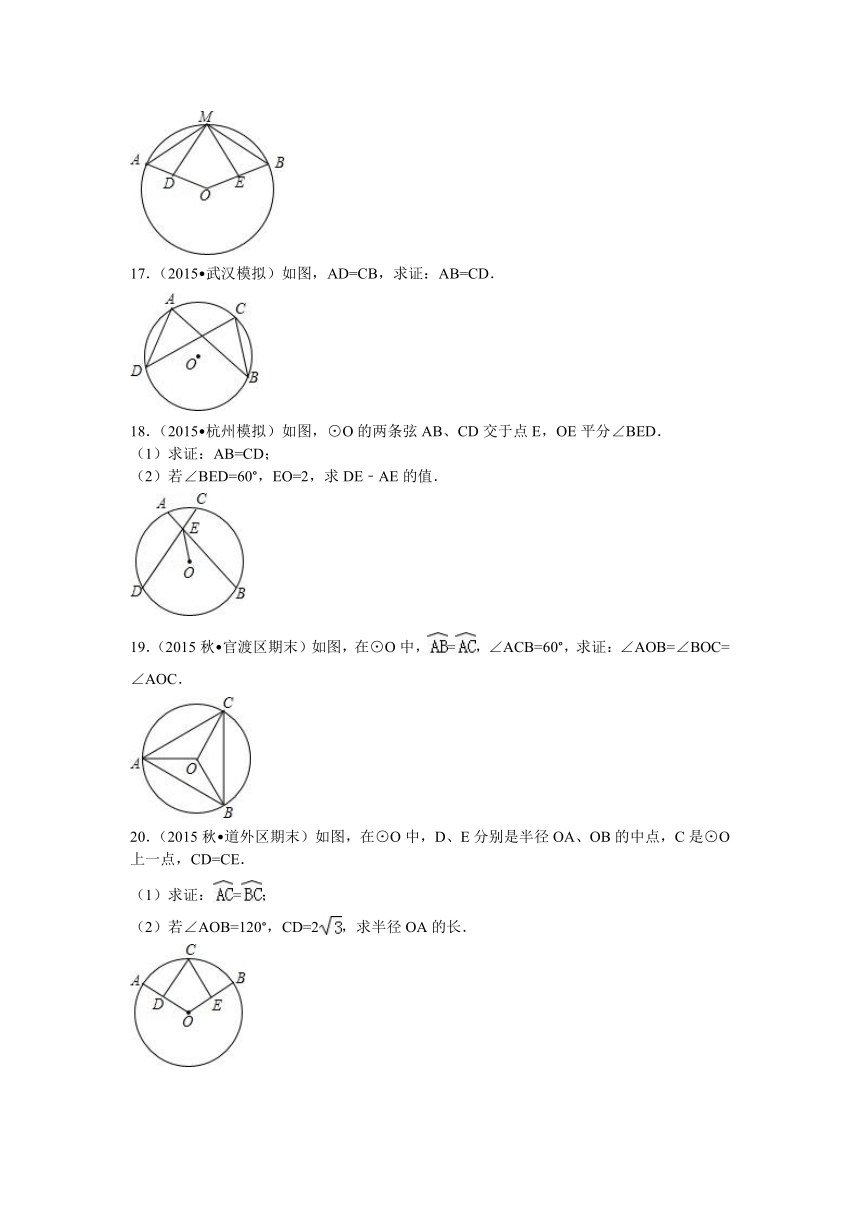
6.(2016 宝山区一模)如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆分别交AB、AC于点D、点E,则弧BD的度数为( )
A.26°
B.64°
C.52°
D.128°
7.(2015 巴中模拟)圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3:4:6,则∠D的度数为( )
A.60
B.80
C.100
D.120
8.(2015 鄄城县三模)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A.27°
B.54°
C.63°
D.36°
9.(2015 茂名模拟)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( )
A.80°
B.70°
C.60°
D.40°
10.(2015 杭州模拟)已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于( )
A.
B.
C.
D.2
二.填空题(共4小题)
11.(2015 太仓市模拟)如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=______
度.
12.(2015秋 营口校级期中)一条弦把圆分成1:5两部分,则这条弦所对的圆周角的度数是______.
13.(2015秋 连云港期中)如图,在⊙O中,=,若∠AOB=40°,则∠COD=______°.
14.(2016 烟台)如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是______cm.
三.解答题(共6小题)
15.(2016 厦门校级模拟)如图,∠AOB=90°,CD是的三等分点,连接AB分别交OC,OD于点E,F.
求证:AE=BF=CD.
16.(2015 东西湖区校级模拟)如图,M为⊙O上一点,弧MA=弧MB,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.
17.(2015 武汉模拟)如图,AD=CB,求证:AB=CD.
18.(2015 杭州模拟)如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
19.(2015秋 官渡区期末)如图,在⊙O中,=,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
20.(2015秋 道外区期末)如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一点,CD=CE.
(1)求证:=;
(2)若∠AOB=120°,CD=2,求半径OA的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 兰州)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )
A.40°
B.45°
C.50°
D.60°
【分析】根据等腰三角形性质和三角形内角和定理求出∠AOB,根据垂径定理求出AD=BD,根据等腰三角形性质得出∠BOC=∠AOB,代入求出即可.
【解答】解:∵∠A=50°,OA=OB,
∴∠OBA=∠OAB=50°,
∴∠AOB=180°﹣50°﹣50°=80°,
∵点C是的中点,
∴∠BOC=∠AOB=40°,
故选A.
【点评】本题考查了圆心角、弧、弦之间的关系,垂径定理,等腰三角形的性质的应用,注意:在同圆或等圆中,两个圆心角、两条弧、两条弦,其中有一对相等,那么其余两对也相等.
2.(2016 济宁)如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40°
B.30°
C.20°
D.15°
【分析】先由圆心角、弧、弦的关系求出∠AOC=∠AOB=40°,再由圆周角定理即可得出结论.
【解答】解:连接CO,如图:
∵在⊙O中,=,
∴∠AOC=∠AOB,
∵∠AOB=40°,
∴∠AOC=40°,
∴∠ADC=∠AOC=20°,
故选C.
【点评】本题考查了圆心角、弧、弦的关系,圆周角定理;熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.
3.(2016 台湾)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=65°,∠D=60°,则的度数为何?( )
A.25
B.40
C.50
D.55
【分析】连接OB,OC,由半径相等得到三角形OAB,三角形OBC,三角形OCD都为等腰三角形,根据∠A=65°,∠D=60°,求出∠1与∠2的度数,根据的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出的度数.
【解答】解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×65°=50°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣50°﹣60°=40°,
则=40°.
故选B
【点评】此题考查了圆心角、弧、弦的关系,弄清圆心角、弧、弦的关系是解本题的关键.
4.(2016 舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120°
B.135°
C.150°
D.165°
【分析】直接利用翻折变换的性质结合锐角三角函数关系得出∠BOD=30°,再利用弧度与圆心角的关系得出答案.
【解答】解:如图所示:连接BO,过点O作OE⊥AB于点E,
由题意可得:EO=BO,AB∥DC,
可得∠EBO=30°,
故∠BOD=30°,
则∠BOC=150°,
故的度数是150°.
故选:C.
【点评】此题主要考查了翻折变换的性质以及弧度与圆心角的关系,正确得出∠BOD的度数是解题关键.
5.(2016 泰山区模拟)如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A.30
B.45
C.50
D.60
【分析】根据已知条件“过圆心O作OD⊥BC交弧BC于点D、,∠ABC=30°”、及直角三角形OBE的两个锐角互余求得∠BOE=60°;然后根据同弧BD所对的圆周角∠DCB是所对的圆心角∠DOB的一半,求得∠DCB的度数.
【解答】解:∵OD⊥BC,∠ABC=30°,
∴在直角三角形OBE中,
∠BOE=60°(直角三角形的两个锐角互余);
又∵∠DCB=∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠DCB=30°;
故选A.
【点评】本题主要考查了圆周角定理,圆心角、弧、弦的关系.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.
6.(2016 宝山区一模)如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆分别交AB、AC于点D、点E,则弧BD的度数为( )
A.26°
B.64°
C.52°
D.128°
【分析】先利用互余计算出∠B=64°,再利用半径相等和等腰三角形的性质得到∠CDB=∠B=64°,则根据三角形内角和定理可计算出∠BCD,然后根据圆心角的度数等于它所对弧的度数求解.
【解答】解:∵∠C=90°,∠A=26°,
∴∠B=64°,
∵CB=CD,
∴∠CDB=∠B=64°,
∴∠BCD=180°﹣64°﹣64°=52°,
∴的度数为52°.
故选:C.
【点评】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
7.(2015 巴中模拟)圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3:4:6,则∠D的度数为( )
A.60
B.80
C.100
D.120
【分析】根据圆内接四边形的对角互补和四边形的内角和为360度进行分析求解.
【解答】解:∵内接四边形的对角互补,
∴∠A:∠B:∠C:∠D=3:4:6:5
设∠A的度数为3x,则∠B,∠C,∠D的度数分别为4x,6x,5x
∴3x+4x+6x+5x=360°
∴x=20°
∴∠D=100°
故选C.
【点评】本题考查圆内接四边形的对角互补和四边形的内角和为360°的理解及运用.
8.(2015 鄄城县三模)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A.27°
B.54°
C.63°
D.36°
【分析】先根据圆周角定理得到∠ACD=∠AOD=27°,然后利用互余求解.
【解答】解:∵一块直角三角板ABC的斜边AB与量角器的直径重合,
∴点A、B、C、D都在以AB为直径的圆上,
∵点D对应54°,即∠AOD=54°,
∴∠ACD=AOD=27°,
∴∠BCD=90°﹣∠ACD=63°.
故选C.
【点评】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理.
9.(2015 茂名模拟)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( )
A.80°
B.70°
C.60°
D.40°
【分析】由同弧所对的圆心角和圆周角的关系可得,∠AOB=2∠ACB,则结果即可得出.
【解答】解:由题意得,∠ACB=∠AOB=×80°=40°.
故选D.
【点评】本题考查了圆心角、弧、弦的关系,重点是圆周角定理的应用.
10.(2015 杭州模拟)已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于( )
A.
B.
C.
D.2
【分析】如图,连接OC.过点C作CD⊥OA于点D.根据圆心角、弧、弦间的关系知∠COD=30°.在直角△COD中,利用勾股定理、30度角所对的直角边是斜边的一半求得线段OD的长度,易求线段AD的长度.所以在直角△ACB中,利用射影定理来求AC2的值.
【解答】解:如图,连接OC.过点C作CD⊥OA于点D.
∵⊙O的直径为4,
∴AB=4,
∴OA=OC=2.
∵弧AC的度数是30°,
∴∠COD=30°,
∴CD=1,
∴OD==,
则AD=2﹣,
∵AB是直径,
∴∠ACB=90°.
∴AC2=AD AB=(2﹣)×4=8﹣4.
故选C.
【点评】本题考查了圆心角、弧、弦间的关系,勾股定理以及含30度角的直角三角形.注意,射影定理是在直角三角形中应用.
二.填空题(共4小题)
11.(2015 太仓市模拟)如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC= 50
度.
【分析】连接OA、OD,证明△APC≌△DPB和△AOP≌△DOP,求出∠APD的度数,根据邻补角的性质得到答案.
【解答】解:连接OA、OD,
∵AB=CD,
∴=,
∴=,
∴AC=BD,
在△APC和△DPB中,
,
∴△APC≌△DPB,
∴PA=PD,
在△AOP和△DOP中,
,
∴△AOP≌△DOP,
∴∠APO=∠DPO=65°,
∴∠APD=130°,
∴∠APC=50°.
故答案为:50°.
【点评】本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.
12.(2015秋 营口校级期中)一条弦把圆分成1:5两部分,则这条弦所对的圆周角的度数是 30°或150° .
【分析】根据题意画出图形,得出两种情况,求出两段弧的度数,即可求出答案.
【解答】解:
连接OA、OB,
∵一条弦AB把圆分成1:5两部分,如图,
∴弧AC′B的度数是×360°=60°,弧ACB的度数是360°﹣60°=300°,
∴∠AOB=60°,
∴∠ACB=∠AOB=30°,
∴∠AC′B=180°﹣30°=150°,
故答案为:30°或150°.
【点评】本题考查了圆周角定理的应用,注意:在同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半.
13.(2015秋 连云港期中)如图,在⊙O中,=,若∠AOB=40°,则∠COD= 40 °.
【分析】先根据在⊙O中,=,可得出=,再由∠AOB=40°即可得出结论.
【解答】解:∵在⊙O中,=,
∴=,
∵∠AOB=40°,
∴∠COD=∠AOB=40°.
故答案为:40.
【点评】本题考查的是圆心角、弧、弦的关系,即在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
14.(2016 烟台)如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是 5 cm.
【分析】根据题意得到MN=BC,当正方形纸片卷成一个圆柱时,EF卷成一个圆,线段卷成圆上一段弧,该段弧所对的圆心角为×360°,要求圆柱上M,N两点间的距离即求弦MN的长.
【解答】解:根据题意得:EF=AD=BC,MN=2EM=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段EF形成一直径为10cm的圆,线段EF为圆上的一段弧.
所对的圆心角为:×360°=120°,
所以圆柱上M,N两点间的距离为:2×5×sin60°=5cm.
故答案为:5.
【点评】此题实质考查了圆上弦的计算,需要先找出圆心角再根据弦长公式计算,熟练掌握公式及性质是解本题的关键.
三.解答题(共6小题)
15.(2016 厦门校级模拟)如图,∠AOB=90°,CD是的三等分点,连接AB分别交OC,OD于点E,F.
求证:AE=BF=CD.
【分析】连接AC,BD,根据∠AOB=90°得出∠AOC的度数,由等腰三角形的性质求出∠OFE的度数.根据SAS定理得出△ACO≌△DCO,故可得出∠ACO=∠OCD,根据等角对等边可得出AC=AE,同理可得BF=BD,由此可得出结论.
【解答】证明:连接AC,BD,
∵在⊙O中,半径OA⊥OB,C、D为弧AB的三等分点,
∴∠AOC=∠AOB=×90°=30°.
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠AOC=∠BOD=30°,
∴∠OEF=∠OAB+∠AOC=45°+30°=75°,同理∠OFE=75°,
∵C,D是的三等分点,
∴AC=CD=BD,
在△ACO与△DCO中,
,
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴AE=BF=CD.
【点评】本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.
16.(2015 东西湖区校级模拟)如图,M为⊙O上一点,弧MA=弧MB,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.
【分析】连接MO,根据等弧对等弦,则∠MOD=∠MOE,再由角平分线的性质,得出MD=ME.
【解答】证明:连接MO(1分)
∵
∴∠MOD=∠MOE(4分)
又∵MD⊥OA于D,ME⊥OB于E
∴MD=ME(7分)
【点评】本题考查了等弧对等弦,以及角平分线的性质.
17.(2015 武汉模拟)如图,AD=CB,求证:AB=CD.
【分析】同弧所对的圆周角相等,可得出△ADE和△CBE中两组对应角相等,已知两组对应角的夹边相等,可证得△ADE≌△CBE,得AE=CE,DE=BE,从而证得AB=CD.
【解答】证明:∵同弧所对对圆周角相等,
∴∠A=∠C,∠D=∠B.
在△ADE和△CBE中,
,
∴△ADE≌△CBE(ASA).
∴AE=CE,DE=BE,
∴AE+BE=CE+DE,即AB=CD.
【点评】本题主要考查圆周角定理,全等三角形的判定和性质等知识的应用能力.
18.(2015 杭州模拟)如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
【分析】(1)过点O作AB、CD的垂线,垂足为M、N,由角平分线的性质,可得OM=ON,然后由弦心距相等可得弦相等,即AB=CD;
(2)由(1)知,OM=ON,AB=CD,OM⊥AB,ON⊥CD,先由垂径定理可得DN=CN=AM=BM,然后由HL可证Rt△EON≌Rt△EOM,进而可得NE=ME,从而得到AE=CE,然后将DE﹣AE转化为:DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,然后在Rt△EON中,由∠NEO=30°,OE=2,求出NE即可.
【解答】解:(1)过点O作AB、CD的垂线,垂足为M、N,如图1,
∵OE平分∠BED,且OM⊥AB,ON⊥CD,
∴OM=ON,
∴AB=CD;
(2)如图2所示,
由(1)知,OM=ON,AB=CD,OM⊥AB,ON⊥CD,
∴DN=CN=AM=BM,
在Rt△EON与Rt△EOM中,
∵,
∴Rt△EON≌Rt△EOM(HL),
∴NE=ME,
∴CD﹣DN﹣NE=AB﹣BM﹣ME,
即AE=CE,
∴DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,
∵∠BED=60°,OE平分∠BED,
∴∠NEO=BED=30°,
∴ON=OE=1,
在Rt△EON中,由勾股定理得:
NE==,
∴DE﹣AE=2NE=2.
【点评】此题考查了圆心角、弧、弦、弦心距之间的关系,及勾股定理和角平分线的性质,解题的关键是:作弦心距,由弦心距相等得到弦相等.
19.(2015秋 官渡区期末)如图,在⊙O中,=,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
【分析】根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
【解答】证明:∵=,
∴AB=AC
∴△ABC是等腰三角形
∵∠ACB=60°
∴△ABC是等边三角形,
∴AB=BC=CA
∴∠AOB=∠BOC=∠COA.
【点评】本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.
20.(2015秋 道外区期末)如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一点,CD=CE.
(1)求证:=;
(2)若∠AOB=120°,CD=2,求半径OA的长.
【分析】(1)连接OC,由SSS证明△OCD≌△OCE,得出对应角相等∠COD=∠COE,由圆心角,弧,弦的关系即可得出结论;
(2)连接AC,证明△AOC是等边三角形,得出CD⊥OA,由三角函数求出OC,即可得出OA.
【解答】解:(1)证明:连接OC,如图1所示:
∵D、E分别是半径OA、OB的中点,OA=OB,
∴OD=OE,
在△OCD和△OCE中,
,
∴△OCD≌△OCE(SSS),
∴∠COD=∠COE,
∴=;
(2)连接AC,如图2所示:
∵∠AOB=120°,
∴∠COD=∠COE=60°,
∵OC=OA,
∴△AOC是等边三角形,
∵D是OA的中点,
∴CD⊥OA,
∴OC===4,
∴OA=4.
【点评】本题考查的是圆心角,弧,弦的关系、全等三角形的判定与性质、三角函数;证明三角形全等和等边三角形是解决问题的关键.
《圆心角、弧、弦、弦心距之间的关系》
测试卷
一.选择题(共10小题)
1.(2016 兰州)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )
A.40°
B.45°
C.50°
D.60°
2.(2016 济宁)如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40°
B.30°
C.20°
D.15°
3.(2016 台湾)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=65°,∠D=60°,则的度数为何?( )
A.25
B.40
C.50
D.55
4.(2016 舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120°
B.135°
C.150°
D.165°
5.(2016 泰山区模拟)如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A.30
B.45
C.50
D.60
6.(2016 宝山区一模)如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆分别交AB、AC于点D、点E,则弧BD的度数为( )
A.26°
B.64°
C.52°
D.128°
7.(2015 巴中模拟)圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3:4:6,则∠D的度数为( )
A.60
B.80
C.100
D.120
8.(2015 鄄城县三模)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A.27°
B.54°
C.63°
D.36°
9.(2015 茂名模拟)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( )
A.80°
B.70°
C.60°
D.40°
10.(2015 杭州模拟)已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于( )
A.
B.
C.
D.2
二.填空题(共4小题)
11.(2015 太仓市模拟)如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=______
度.
12.(2015秋 营口校级期中)一条弦把圆分成1:5两部分,则这条弦所对的圆周角的度数是______.
13.(2015秋 连云港期中)如图,在⊙O中,=,若∠AOB=40°,则∠COD=______°.
14.(2016 烟台)如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是______cm.
三.解答题(共6小题)
15.(2016 厦门校级模拟)如图,∠AOB=90°,CD是的三等分点,连接AB分别交OC,OD于点E,F.
求证:AE=BF=CD.
16.(2015 东西湖区校级模拟)如图,M为⊙O上一点,弧MA=弧MB,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.
17.(2015 武汉模拟)如图,AD=CB,求证:AB=CD.
18.(2015 杭州模拟)如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
19.(2015秋 官渡区期末)如图,在⊙O中,=,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
20.(2015秋 道外区期末)如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一点,CD=CE.
(1)求证:=;
(2)若∠AOB=120°,CD=2,求半径OA的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 兰州)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )
A.40°
B.45°
C.50°
D.60°
【分析】根据等腰三角形性质和三角形内角和定理求出∠AOB,根据垂径定理求出AD=BD,根据等腰三角形性质得出∠BOC=∠AOB,代入求出即可.
【解答】解:∵∠A=50°,OA=OB,
∴∠OBA=∠OAB=50°,
∴∠AOB=180°﹣50°﹣50°=80°,
∵点C是的中点,
∴∠BOC=∠AOB=40°,
故选A.
【点评】本题考查了圆心角、弧、弦之间的关系,垂径定理,等腰三角形的性质的应用,注意:在同圆或等圆中,两个圆心角、两条弧、两条弦,其中有一对相等,那么其余两对也相等.
2.(2016 济宁)如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40°
B.30°
C.20°
D.15°
【分析】先由圆心角、弧、弦的关系求出∠AOC=∠AOB=40°,再由圆周角定理即可得出结论.
【解答】解:连接CO,如图:
∵在⊙O中,=,
∴∠AOC=∠AOB,
∵∠AOB=40°,
∴∠AOC=40°,
∴∠ADC=∠AOC=20°,
故选C.
【点评】本题考查了圆心角、弧、弦的关系,圆周角定理;熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.
3.(2016 台湾)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=65°,∠D=60°,则的度数为何?( )
A.25
B.40
C.50
D.55
【分析】连接OB,OC,由半径相等得到三角形OAB,三角形OBC,三角形OCD都为等腰三角形,根据∠A=65°,∠D=60°,求出∠1与∠2的度数,根据的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出的度数.
【解答】解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×65°=50°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣50°﹣60°=40°,
则=40°.
故选B
【点评】此题考查了圆心角、弧、弦的关系,弄清圆心角、弧、弦的关系是解本题的关键.
4.(2016 舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120°
B.135°
C.150°
D.165°
【分析】直接利用翻折变换的性质结合锐角三角函数关系得出∠BOD=30°,再利用弧度与圆心角的关系得出答案.
【解答】解:如图所示:连接BO,过点O作OE⊥AB于点E,
由题意可得:EO=BO,AB∥DC,
可得∠EBO=30°,
故∠BOD=30°,
则∠BOC=150°,
故的度数是150°.
故选:C.
【点评】此题主要考查了翻折变换的性质以及弧度与圆心角的关系,正确得出∠BOD的度数是解题关键.
5.(2016 泰山区模拟)如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A.30
B.45
C.50
D.60
【分析】根据已知条件“过圆心O作OD⊥BC交弧BC于点D、,∠ABC=30°”、及直角三角形OBE的两个锐角互余求得∠BOE=60°;然后根据同弧BD所对的圆周角∠DCB是所对的圆心角∠DOB的一半,求得∠DCB的度数.
【解答】解:∵OD⊥BC,∠ABC=30°,
∴在直角三角形OBE中,
∠BOE=60°(直角三角形的两个锐角互余);
又∵∠DCB=∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠DCB=30°;
故选A.
【点评】本题主要考查了圆周角定理,圆心角、弧、弦的关系.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.
6.(2016 宝山区一模)如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆分别交AB、AC于点D、点E,则弧BD的度数为( )
A.26°
B.64°
C.52°
D.128°
【分析】先利用互余计算出∠B=64°,再利用半径相等和等腰三角形的性质得到∠CDB=∠B=64°,则根据三角形内角和定理可计算出∠BCD,然后根据圆心角的度数等于它所对弧的度数求解.
【解答】解:∵∠C=90°,∠A=26°,
∴∠B=64°,
∵CB=CD,
∴∠CDB=∠B=64°,
∴∠BCD=180°﹣64°﹣64°=52°,
∴的度数为52°.
故选:C.
【点评】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
7.(2015 巴中模拟)圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3:4:6,则∠D的度数为( )
A.60
B.80
C.100
D.120
【分析】根据圆内接四边形的对角互补和四边形的内角和为360度进行分析求解.
【解答】解:∵内接四边形的对角互补,
∴∠A:∠B:∠C:∠D=3:4:6:5
设∠A的度数为3x,则∠B,∠C,∠D的度数分别为4x,6x,5x
∴3x+4x+6x+5x=360°
∴x=20°
∴∠D=100°
故选C.
【点评】本题考查圆内接四边形的对角互补和四边形的内角和为360°的理解及运用.
8.(2015 鄄城县三模)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A.27°
B.54°
C.63°
D.36°
【分析】先根据圆周角定理得到∠ACD=∠AOD=27°,然后利用互余求解.
【解答】解:∵一块直角三角板ABC的斜边AB与量角器的直径重合,
∴点A、B、C、D都在以AB为直径的圆上,
∵点D对应54°,即∠AOD=54°,
∴∠ACD=AOD=27°,
∴∠BCD=90°﹣∠ACD=63°.
故选C.
【点评】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理.
9.(2015 茂名模拟)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( )
A.80°
B.70°
C.60°
D.40°
【分析】由同弧所对的圆心角和圆周角的关系可得,∠AOB=2∠ACB,则结果即可得出.
【解答】解:由题意得,∠ACB=∠AOB=×80°=40°.
故选D.
【点评】本题考查了圆心角、弧、弦的关系,重点是圆周角定理的应用.
10.(2015 杭州模拟)已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于( )
A.
B.
C.
D.2
【分析】如图,连接OC.过点C作CD⊥OA于点D.根据圆心角、弧、弦间的关系知∠COD=30°.在直角△COD中,利用勾股定理、30度角所对的直角边是斜边的一半求得线段OD的长度,易求线段AD的长度.所以在直角△ACB中,利用射影定理来求AC2的值.
【解答】解:如图,连接OC.过点C作CD⊥OA于点D.
∵⊙O的直径为4,
∴AB=4,
∴OA=OC=2.
∵弧AC的度数是30°,
∴∠COD=30°,
∴CD=1,
∴OD==,
则AD=2﹣,
∵AB是直径,
∴∠ACB=90°.
∴AC2=AD AB=(2﹣)×4=8﹣4.
故选C.
【点评】本题考查了圆心角、弧、弦间的关系,勾股定理以及含30度角的直角三角形.注意,射影定理是在直角三角形中应用.
二.填空题(共4小题)
11.(2015 太仓市模拟)如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC= 50
度.
【分析】连接OA、OD,证明△APC≌△DPB和△AOP≌△DOP,求出∠APD的度数,根据邻补角的性质得到答案.
【解答】解:连接OA、OD,
∵AB=CD,
∴=,
∴=,
∴AC=BD,
在△APC和△DPB中,
,
∴△APC≌△DPB,
∴PA=PD,
在△AOP和△DOP中,
,
∴△AOP≌△DOP,
∴∠APO=∠DPO=65°,
∴∠APD=130°,
∴∠APC=50°.
故答案为:50°.
【点评】本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.
12.(2015秋 营口校级期中)一条弦把圆分成1:5两部分,则这条弦所对的圆周角的度数是 30°或150° .
【分析】根据题意画出图形,得出两种情况,求出两段弧的度数,即可求出答案.
【解答】解:
连接OA、OB,
∵一条弦AB把圆分成1:5两部分,如图,
∴弧AC′B的度数是×360°=60°,弧ACB的度数是360°﹣60°=300°,
∴∠AOB=60°,
∴∠ACB=∠AOB=30°,
∴∠AC′B=180°﹣30°=150°,
故答案为:30°或150°.
【点评】本题考查了圆周角定理的应用,注意:在同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半.
13.(2015秋 连云港期中)如图,在⊙O中,=,若∠AOB=40°,则∠COD= 40 °.
【分析】先根据在⊙O中,=,可得出=,再由∠AOB=40°即可得出结论.
【解答】解:∵在⊙O中,=,
∴=,
∵∠AOB=40°,
∴∠COD=∠AOB=40°.
故答案为:40.
【点评】本题考查的是圆心角、弧、弦的关系,即在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
14.(2016 烟台)如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是 5 cm.
【分析】根据题意得到MN=BC,当正方形纸片卷成一个圆柱时,EF卷成一个圆,线段卷成圆上一段弧,该段弧所对的圆心角为×360°,要求圆柱上M,N两点间的距离即求弦MN的长.
【解答】解:根据题意得:EF=AD=BC,MN=2EM=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段EF形成一直径为10cm的圆,线段EF为圆上的一段弧.
所对的圆心角为:×360°=120°,
所以圆柱上M,N两点间的距离为:2×5×sin60°=5cm.
故答案为:5.
【点评】此题实质考查了圆上弦的计算,需要先找出圆心角再根据弦长公式计算,熟练掌握公式及性质是解本题的关键.
三.解答题(共6小题)
15.(2016 厦门校级模拟)如图,∠AOB=90°,CD是的三等分点,连接AB分别交OC,OD于点E,F.
求证:AE=BF=CD.
【分析】连接AC,BD,根据∠AOB=90°得出∠AOC的度数,由等腰三角形的性质求出∠OFE的度数.根据SAS定理得出△ACO≌△DCO,故可得出∠ACO=∠OCD,根据等角对等边可得出AC=AE,同理可得BF=BD,由此可得出结论.
【解答】证明:连接AC,BD,
∵在⊙O中,半径OA⊥OB,C、D为弧AB的三等分点,
∴∠AOC=∠AOB=×90°=30°.
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠AOC=∠BOD=30°,
∴∠OEF=∠OAB+∠AOC=45°+30°=75°,同理∠OFE=75°,
∵C,D是的三等分点,
∴AC=CD=BD,
在△ACO与△DCO中,
,
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴AE=BF=CD.
【点评】本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.
16.(2015 东西湖区校级模拟)如图,M为⊙O上一点,弧MA=弧MB,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.
【分析】连接MO,根据等弧对等弦,则∠MOD=∠MOE,再由角平分线的性质,得出MD=ME.
【解答】证明:连接MO(1分)
∵
∴∠MOD=∠MOE(4分)
又∵MD⊥OA于D,ME⊥OB于E
∴MD=ME(7分)
【点评】本题考查了等弧对等弦,以及角平分线的性质.
17.(2015 武汉模拟)如图,AD=CB,求证:AB=CD.
【分析】同弧所对的圆周角相等,可得出△ADE和△CBE中两组对应角相等,已知两组对应角的夹边相等,可证得△ADE≌△CBE,得AE=CE,DE=BE,从而证得AB=CD.
【解答】证明:∵同弧所对对圆周角相等,
∴∠A=∠C,∠D=∠B.
在△ADE和△CBE中,
,
∴△ADE≌△CBE(ASA).
∴AE=CE,DE=BE,
∴AE+BE=CE+DE,即AB=CD.
【点评】本题主要考查圆周角定理,全等三角形的判定和性质等知识的应用能力.
18.(2015 杭州模拟)如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
【分析】(1)过点O作AB、CD的垂线,垂足为M、N,由角平分线的性质,可得OM=ON,然后由弦心距相等可得弦相等,即AB=CD;
(2)由(1)知,OM=ON,AB=CD,OM⊥AB,ON⊥CD,先由垂径定理可得DN=CN=AM=BM,然后由HL可证Rt△EON≌Rt△EOM,进而可得NE=ME,从而得到AE=CE,然后将DE﹣AE转化为:DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,然后在Rt△EON中,由∠NEO=30°,OE=2,求出NE即可.
【解答】解:(1)过点O作AB、CD的垂线,垂足为M、N,如图1,
∵OE平分∠BED,且OM⊥AB,ON⊥CD,
∴OM=ON,
∴AB=CD;
(2)如图2所示,
由(1)知,OM=ON,AB=CD,OM⊥AB,ON⊥CD,
∴DN=CN=AM=BM,
在Rt△EON与Rt△EOM中,
∵,
∴Rt△EON≌Rt△EOM(HL),
∴NE=ME,
∴CD﹣DN﹣NE=AB﹣BM﹣ME,
即AE=CE,
∴DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,
∵∠BED=60°,OE平分∠BED,
∴∠NEO=BED=30°,
∴ON=OE=1,
在Rt△EON中,由勾股定理得:
NE==,
∴DE﹣AE=2NE=2.
【点评】此题考查了圆心角、弧、弦、弦心距之间的关系,及勾股定理和角平分线的性质,解题的关键是:作弦心距,由弦心距相等得到弦相等.
19.(2015秋 官渡区期末)如图,在⊙O中,=,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
【分析】根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
【解答】证明:∵=,
∴AB=AC
∴△ABC是等腰三角形
∵∠ACB=60°
∴△ABC是等边三角形,
∴AB=BC=CA
∴∠AOB=∠BOC=∠COA.
【点评】本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.
20.(2015秋 道外区期末)如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一点,CD=CE.
(1)求证:=;
(2)若∠AOB=120°,CD=2,求半径OA的长.
【分析】(1)连接OC,由SSS证明△OCD≌△OCE,得出对应角相等∠COD=∠COE,由圆心角,弧,弦的关系即可得出结论;
(2)连接AC,证明△AOC是等边三角形,得出CD⊥OA,由三角函数求出OC,即可得出OA.
【解答】解:(1)证明:连接OC,如图1所示:
∵D、E分别是半径OA、OB的中点,OA=OB,
∴OD=OE,
在△OCD和△OCE中,
,
∴△OCD≌△OCE(SSS),
∴∠COD=∠COE,
∴=;
(2)连接AC,如图2所示:
∵∠AOB=120°,
∴∠COD=∠COE=60°,
∵OC=OA,
∴△AOC是等边三角形,
∵D是OA的中点,
∴CD⊥OA,
∴OC===4,
∴OA=4.
【点评】本题考查的是圆心角,弧,弦的关系、全等三角形的判定与性质、三角函数;证明三角形全等和等边三角形是解决问题的关键.
