沪科版九年级数学下册24.1.1图形的旋转测试卷(解析版)
文档属性
| 名称 | 沪科版九年级数学下册24.1.1图形的旋转测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 315.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-04 22:51:13 | ||
图片预览


文档简介
沪科版九年级数学下册24.1.1《图形的旋转》测试卷
一.选择题(共10小题)
1.(2016 呼和浩特)将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96
B.69
C.66
D.99
2.(2016 江西模拟)如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.
B.
C.
D.
3.(2016 呼伦贝尔校级一模)下面生活中的实例,不是旋转的是( )
A.传送带传送货物
B.螺旋桨的运动
C.风车风轮的运动
D.自行车车轮的运动
4.(2016 兰州)如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.πcm
B.2πcm
C.3πcm
D.5πcm
5.(2016 道外区二模)下列图形中,旋转对称图形有( )个.
A.1
B.2
C.3
D.4
6.(2016春 南安市期末)下列现象中,不属于旋转的是( )
A.汽车在笔直的公路上行驶
B.大风车的转动
C.电风扇叶片的转动
D.时针的转动
7.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
8.(2016春 巨野县期末)下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
A.
B.
C.
D.
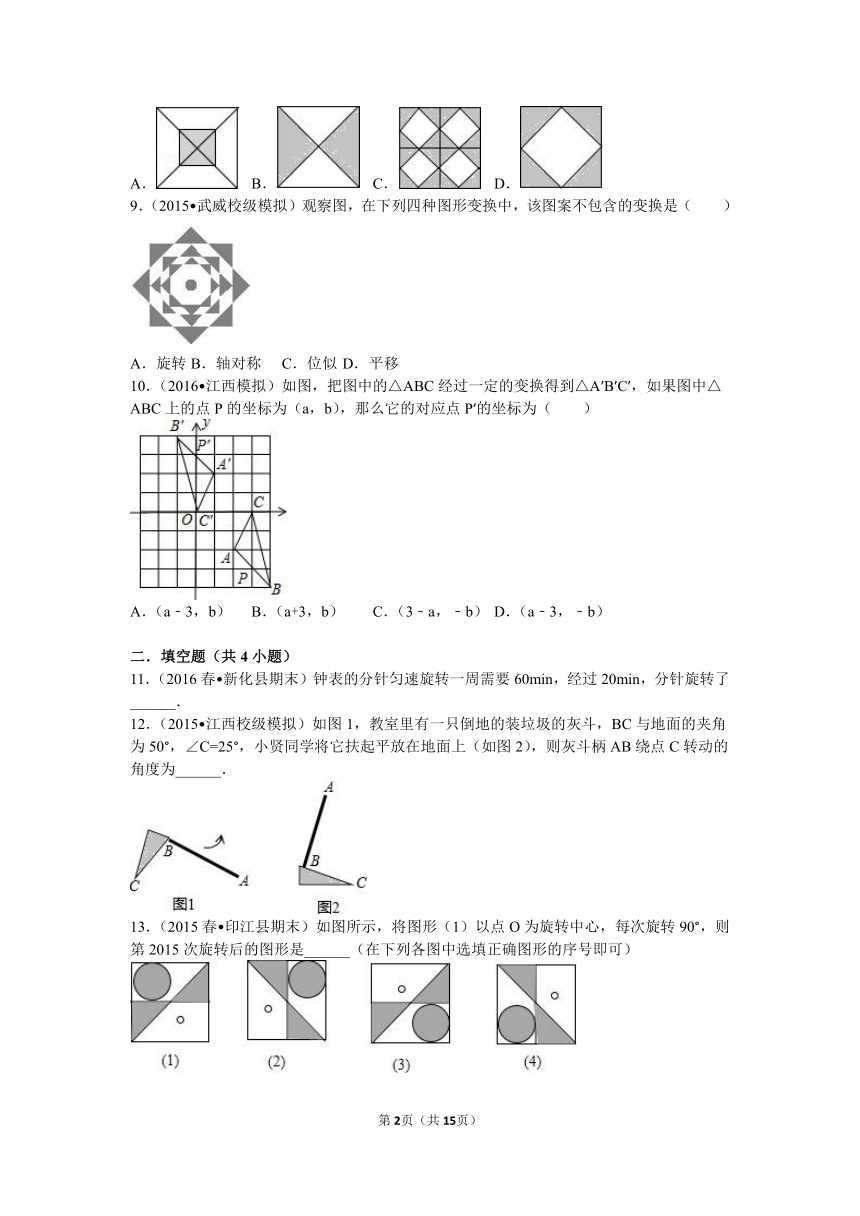
9.(2015 武威校级模拟)观察图,在下列四种图形变换中,该图案不包含的变换是( )
A.旋转
B.轴对称
C.位似
D.平移
10.(2016 江西模拟)如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
A.(a﹣3,b)
B.(a+3,b)
C.(3﹣a,﹣b)
D.(a﹣3,﹣b)
二.填空题(共4小题)
11.(2016春 新化县期末)钟表的分针匀速旋转一周需要60min,经过20min,分针旋转了______.
12.(2015 江西校级模拟)如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为______.
13.(2015春 印江县期末)如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是______(在下列各图中选填正确图形的序号即可)
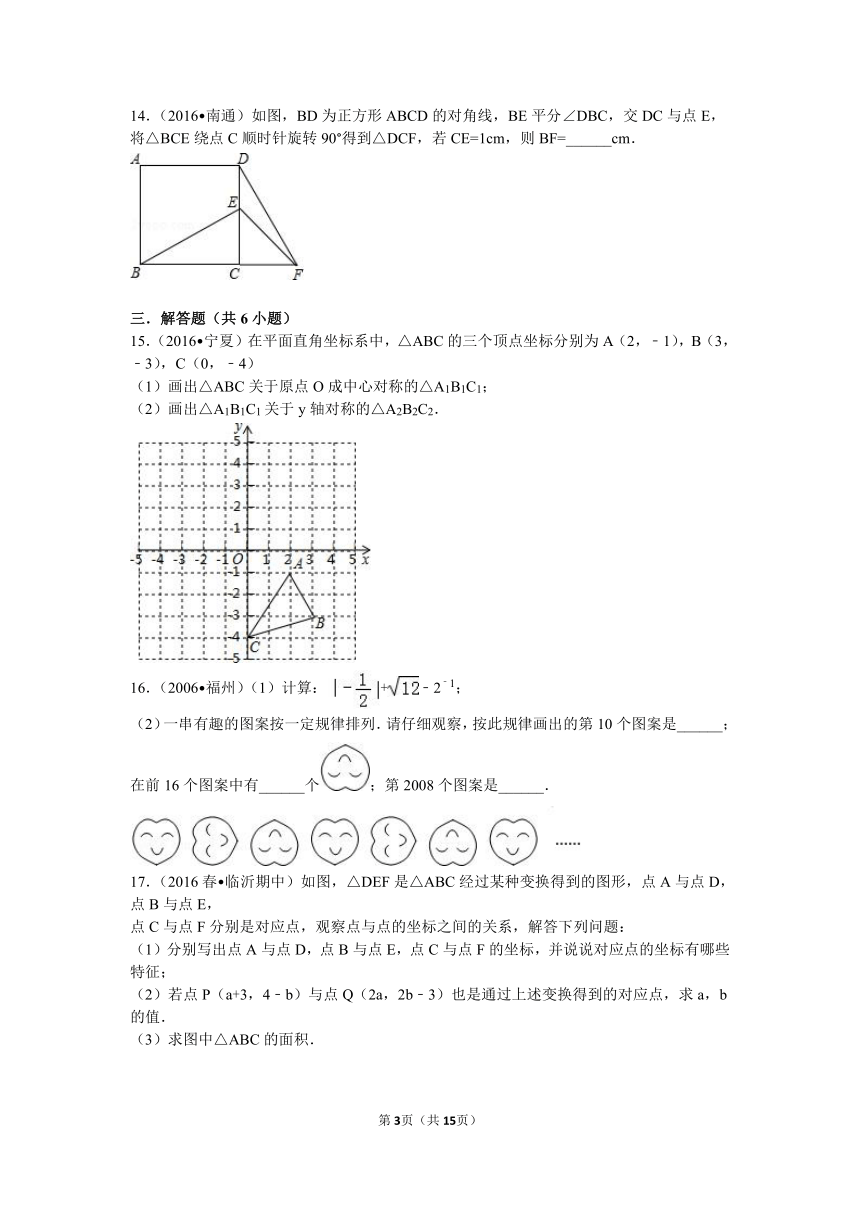
14.(2016 南通)如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF=______cm.
三.解答题(共6小题)
15.(2016 宁夏)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣1),B(3,﹣3),C(0,﹣4)
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
16.(2006 福州)(1)计算:+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是______;在前16个图案中有______个;第2008个图案是______.
17.(2016春 临沂期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
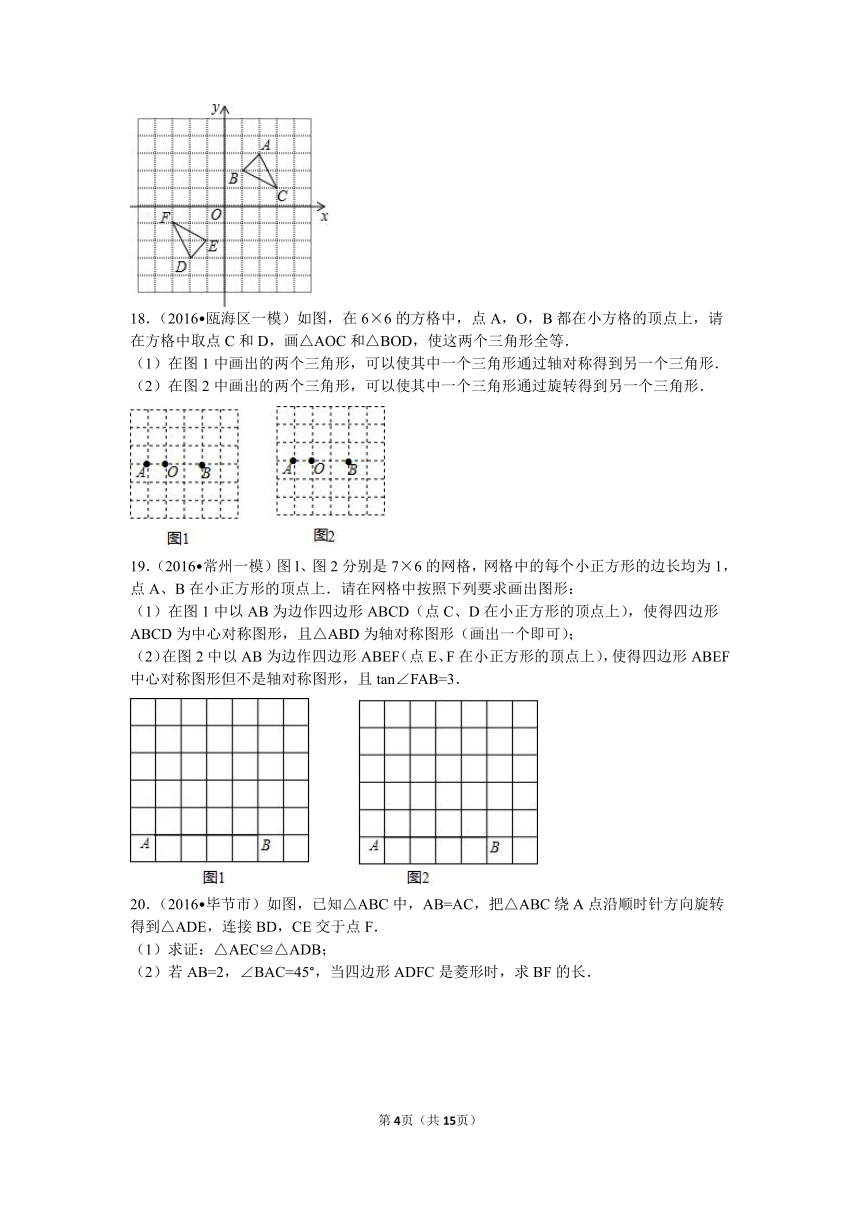
18.(2016 瓯海区一模)如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和D,画△AOC和△BOD,使这两个三角形全等.
(1)在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形.
(2)在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.
19.(2016 常州一模)图l、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.请在网格中按照下列要求画出图形:
(1)在图1中以AB为边作四边形ABCD(点C、D在小正方形的顶点上),使得四边形ABCD为中心对称图形,且△ABD为轴对称图形(画出一个即可);
(2)在图2中以AB为边作四边形ABEF(点E、F在小正方形的顶点上),使得四边形ABEF中心对称图形但不是轴对称图形,且tan∠FAB=3.
20.(2016 毕节市)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 呼和浩特)将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96
B.69
C.66
D.99
【分析】直接利用中心对称图形的性质结合69的特点得出答案.
【解答】解:现将数字“69”旋转180°,得到的数字是:69.
故选:B.
【点评】此题主要考查了生活中的旋转现象,正确想象出旋转后图形是解题关键.
2.(2016 江西模拟)如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.
B.
C.
D.
【分析】根据△ABC绕着点O逆时针旋转90°,得出各对应点的位置判断即可;
【解答】解:根据旋转的性质和旋转的方向得:△ABC绕O点按逆时针旋转90°后的图案是A,
故选A.
【点评】本题考查了旋转的性质,知道想要确定旋转后的图形①要确定旋转的方向②要确定旋转的大小是解题的关键.
3.(2016 呼伦贝尔校级一模)下面生活中的实例,不是旋转的是( )
A.传送带传送货物
B.螺旋桨的运动
C.风车风轮的运动
D.自行车车轮的运动
【分析】根据旋转的定义来判断:旋转就是将图形绕某点转动一定的角度,旋转后所得图形与原图形的形状、大小不变,对应点与旋转中心的连线的夹角相等.
【解答】解:传送带传送货物的过程中没有发生旋转.
故选:A.
【点评】本题考查了旋转,正确理解旋转的定义是解题的关键.
4.(2016 兰州)如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.πcm
B.2πcm
C.3πcm
D.5πcm
【分析】根据定滑轮的性质得到重物上升的即为转过的弧长,利用弧长公式计算即可.
【解答】解:根据题意得:l==3πcm,
则重物上升了3πcm,
故选C
【点评】此题考查了旋转的性质,以及弧长公式,熟练掌握旋转的性质是解本题的关键.
5.(2016 道外区二模)下列图形中,旋转对称图形有( )个.
A.1
B.2
C.3
D.4
【分析】根据旋转对称图形的定义对四个图形进行分析即可.
【解答】解:旋转对称图形是从左起第(1),(2),(4);不是旋转对称图形的是(3).
故选:C.
【点评】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
6.(2016春 南安市期末)下列现象中,不属于旋转的是( )
A.汽车在笔直的公路上行驶
B.大风车的转动
C.电风扇叶片的转动
D.时针的转动
【分析】根据旋转的定义分析求解.
【解答】解:因为在平面内,把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转,而汽车在笔直的公路上行驶是一种复合运动,车轮在旋转的同时又在作平移运动,
所以汽车在笔直的公路上行驶不属于旋转.
故:选A
【点评】本题考查了生活中的旋转现象;旋转是围绕一点旋转一定的角度的图形变换,因而旋转一定有旋转中心和旋转角,且旋转前后图形能够重合,这时判断旋转的关键
7.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
【分析】根据旋转的性质,△AOB绕点O旋转180°得到△DOE,点A与点D、B与E关于点O成中心对称解答.
【解答】解:∵△AOB绕点O旋转180°得到△DOE,
∴作图正确是C选项图形.
故选C.
【点评】本题考查了利用旋转变换作图,熟记旋转的性质,判断出对应点关于点O对称是解题的关键.
8.(2016春 巨野县期末)下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
A.
B.
C.
D.
【分析】分别根据旋转的定义及平移的定义逐项分析即可.
【解答】解:
A、B、C、D四个选项中的图形都可以看成是图形的一半旋转180°得到,
若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,
故A、B、D不能由平移得到,只有C选项的图形,可看成是由基本图形通过平移得到,
故选C.
【点评】本题主要考查旋转和平移的定义,掌握平移和旋转的特征是解题的关键.
9.(2015 武威校级模拟)观察图,在下列四种图形变换中,该图案不包含的变换是( )
A.旋转
B.轴对称
C.位似
D.平移
【分析】根据平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是一个图形沿一条直线对着直线两旁的部分能完全重合,位似是相似图形的每组对应点所在的直线都经过同一个点,可得答案.
【解答】解:A、大小相同的图形是旋转得到的,故A正确;
B、一个图形沿一条直线对着直线两旁的部分能完全重合,故B正确;
C、位置相同、形状相同的图案、大小不同的图形是位似得到的,故C正确;
D、图形没有平移,故D错误;
故选:D.
【点评】本题考查了几何变换的类型,平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是一个图形沿一条直线对着直线两旁的部分能完全重合,位似是相似图形的每组对应点所在的直线都经过同一个点,观察时要紧扣图形变换特点,认真判断.
10.(2016 江西模拟)如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
A.(a﹣3,b)
B.(a+3,b)
C.(3﹣a,﹣b)
D.(a﹣3,﹣b)
【分析】先根据图形确定出对称中心,然后根据中点公式列式计算即可得解.
【解答】解:由图可知,△ABC与△A′B′C′关于点(1.5,0)成中心对称,
设点P′的坐标为(x,y),
所以,=1.5,=0,
解得x=3﹣a,y=﹣b,
所以,P′(3﹣a,﹣b).
故选:C.
【点评】本题考查了坐标与图形变化﹣旋转,准确识图,观察出两三角形成中心对称,对称中心是(1.5,0)是解题的关键.
二.填空题(共4小题)
11.(2016春 新化县期末)钟表的分针匀速旋转一周需要60min,经过20min,分针旋转了 120° .
【分析】钟表的分针匀速旋转一周需要60分,分针旋转了360°;求经过20分,分针的旋转度数,列出算式,解答出即可.
【解答】解:根据题意得,×360°=120°.
故答案为:120°.
【点评】本题考查了生活中的旋转现象,明确分针旋转一周,分针旋转了360°是解答本题的关键.
12.(2015 江西校级模拟)如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为 105° .
【分析】连结AC并且延长至E,根据旋转的性质和平角的定义,由角的和差关系即可求解.
【解答】解:如图:连结AC并且延长至E,
∠DCE=180°﹣∠DCB﹣∠ACB=105°.
故灰斗柄AB绕点C转动的角度为105°.
故答案为:105°.
【点评】考查了生活中的旋转现象,本题关键是由角的和差关系得到∠DCE的度数.
13.(2015春 印江县期末)如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是 (4) (在下列各图中选填正确图形的序号即可)
【分析】观察图形变化,图形(1)以点O为旋转中心,每次顺时针旋转90°,且每4次一个循环,由于2015=503×4+3,则第2015次旋转后的图形与(4)一样.
【解答】解:观察图形,将图形(1)以点O为旋转中心,每次顺时针旋转90°,得到下一个图形,每旋转四次回到原来的位置,
而2015=503×4+3,
所以第2015次旋转后的图形与(4)一样.
故答案为(4).
【点评】本题考查了生活中的旋转现象:在平面内,把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的角叫做旋转角.可以通过旋转得到很大美丽的图案.
14.(2016 南通)如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF= 2+ cm.
【分析】过点E作EM⊥BD于点M,则△DEM为等腰直角三角形,根据角平分线以及等腰直角三角形的性质即可得出DE的长度,再根据正方形以及旋转的性质即可得出线段BF的长.
【解答】解:过点E作EM⊥BD于点M,如图所示.
∵四边形ABCD为正方形,
∴∠BAC=45°,∠BCD=90°,
∴△DEM为等腰直角三角形.
∵BE平分∠DBC,EM⊥BD,
∴EM=EC=1cm,
∴DE=EM=cm.
由旋转的性质可知:CF=CE=1cm,
∴BF=BC+CF=CE+DE+CF=1++1=2+cm.
故答案为:2+.
【点评】本题考查了旋转的性质、正方形的性质以及角平分线的性质,解题的关键是求出线段BC以及CF的长度.本题属于基础题,难度不大,解决该题型题目时,结合角平分线以及等腰直角三角形的性质求出线段的长度是关键.
三.解答题(共6小题)
15.(2016 宁夏)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣1),B(3,﹣3),C(0,﹣4)
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
【分析】(1)根据网格结构找出点A、B、C关于原点对称的点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A1、B1、C1关于y轴对称的点A2、B2、C2的位置,然后顺次连接即可.
【解答】解:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示.
【点评】本题考查了利用旋转变换作图,利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
16.(2006 福州)(1)计算:+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 5 个;第2008个图案是 .
【分析】(1)根据绝对值,二次根式的性质化简原式,可得答案;
(2)分析可得,图形三个一组,且依次循环;10除3的余数为1,2008除3的余数为1,故第10个图案与第2008个图案相同,都是第一个图案,即;在前16个图案中有共5组,第六组只有第一个图案;故在前16个图案中有5个.
【解答】解:(1)原式==2;
(2)根据分析,知应分别为,5,.
【点评】本题考查代数式的化简及根据图形找规律的方法.
17.(2016春 临沂期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
【分析】(1)根据图形即可直接写出坐标;
(2)根据(1)中得到的横纵坐标之间的关系可以列方程求解;
(3)转化为图形的面积的和、差即可求解.
【解答】解:(1)A(2,3)与D(﹣2,﹣3);B(1,2)与E(﹣1,﹣2);C(3,1)与F(﹣3,﹣1).
对应点的坐标的特征:横坐标互为相反数,纵坐标互为相反数;
(2)由(1)可得a+3=﹣2a,4﹣b=﹣(2b﹣3).解得a=﹣1,b=﹣1;
(3)三角形ABC的面积=2×2﹣×2×1﹣×2×1﹣×1×1=.
【点评】本题考查了图形的中心对称变换,写出点的坐标得到对称的点之间的关系是关键.
18.(2016 瓯海区一模)如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和D,画△AOC和△BOD,使这两个三角形全等.
(1)在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形.
(2)在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.
【分析】(1)直接利用轴对称图形的性质得出符合题意的答案;
(2)直接利用旋转的性质得出符合题意的答案.
【解答】解:(1)如图1所示:△ACO,△DOB即为所求;
(2)如图2所示:△ACO,△DOB即为所求.
【点评】此题主要考查了轴对称变换以及旋转变换,正确得出对应点位置是解题关键.
19.(2016 常州一模)图l、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.请在网格中按照下列要求画出图形:
(1)在图1中以AB为边作四边形ABCD(点C、D在小正方形的顶点上),使得四边形ABCD为中心对称图形,且△ABD为轴对称图形(画出一个即可);
(2)在图2中以AB为边作四边形ABEF(点E、F在小正方形的顶点上),使得四边形ABEF中心对称图形但不是轴对称图形,且tan∠FAB=3.
【分析】(1)根据轴对称图形以及中心对称图形的性质得出符合题意的图形即可;
(2)利用轴对称图形以及中心对称图形的性质,再利用锐角三角函数关系得出答案.
【解答】解:(1)如图1所示:
(2)如图2所示.
【点评】此题主要考查了旋转变换以及轴对称变换,正确把握锐角三角函数关系是解题关键.
20.(2016 毕节市)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
【分析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是菱形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为等腰直角三角形,求出BD的长,由BD﹣DF求出BF的长即可.
【解答】解:(1)由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS);
(2)∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:AB=AD,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴BD2=2AB2,即BD=2,
∴AD=DF=FC=AC=AB=2,
∴BF=BD﹣DF=2﹣2.
【点评】此题考查了旋转的性质,全等三角形的判定与性质,以及菱形的性质,熟练掌握旋转的性质是解本题的关键.
第1页(共1页)
一.选择题(共10小题)
1.(2016 呼和浩特)将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96
B.69
C.66
D.99
2.(2016 江西模拟)如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.
B.
C.
D.
3.(2016 呼伦贝尔校级一模)下面生活中的实例,不是旋转的是( )
A.传送带传送货物
B.螺旋桨的运动
C.风车风轮的运动
D.自行车车轮的运动
4.(2016 兰州)如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.πcm
B.2πcm
C.3πcm
D.5πcm
5.(2016 道外区二模)下列图形中,旋转对称图形有( )个.
A.1
B.2
C.3
D.4
6.(2016春 南安市期末)下列现象中,不属于旋转的是( )
A.汽车在笔直的公路上行驶
B.大风车的转动
C.电风扇叶片的转动
D.时针的转动
7.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
8.(2016春 巨野县期末)下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
A.
B.
C.
D.
9.(2015 武威校级模拟)观察图,在下列四种图形变换中,该图案不包含的变换是( )
A.旋转
B.轴对称
C.位似
D.平移
10.(2016 江西模拟)如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
A.(a﹣3,b)
B.(a+3,b)
C.(3﹣a,﹣b)
D.(a﹣3,﹣b)
二.填空题(共4小题)
11.(2016春 新化县期末)钟表的分针匀速旋转一周需要60min,经过20min,分针旋转了______.
12.(2015 江西校级模拟)如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为______.
13.(2015春 印江县期末)如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是______(在下列各图中选填正确图形的序号即可)
14.(2016 南通)如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF=______cm.
三.解答题(共6小题)
15.(2016 宁夏)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣1),B(3,﹣3),C(0,﹣4)
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
16.(2006 福州)(1)计算:+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是______;在前16个图案中有______个;第2008个图案是______.
17.(2016春 临沂期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
18.(2016 瓯海区一模)如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和D,画△AOC和△BOD,使这两个三角形全等.
(1)在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形.
(2)在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.
19.(2016 常州一模)图l、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.请在网格中按照下列要求画出图形:
(1)在图1中以AB为边作四边形ABCD(点C、D在小正方形的顶点上),使得四边形ABCD为中心对称图形,且△ABD为轴对称图形(画出一个即可);
(2)在图2中以AB为边作四边形ABEF(点E、F在小正方形的顶点上),使得四边形ABEF中心对称图形但不是轴对称图形,且tan∠FAB=3.
20.(2016 毕节市)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 呼和浩特)将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96
B.69
C.66
D.99
【分析】直接利用中心对称图形的性质结合69的特点得出答案.
【解答】解:现将数字“69”旋转180°,得到的数字是:69.
故选:B.
【点评】此题主要考查了生活中的旋转现象,正确想象出旋转后图形是解题关键.
2.(2016 江西模拟)如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.
B.
C.
D.
【分析】根据△ABC绕着点O逆时针旋转90°,得出各对应点的位置判断即可;
【解答】解:根据旋转的性质和旋转的方向得:△ABC绕O点按逆时针旋转90°后的图案是A,
故选A.
【点评】本题考查了旋转的性质,知道想要确定旋转后的图形①要确定旋转的方向②要确定旋转的大小是解题的关键.
3.(2016 呼伦贝尔校级一模)下面生活中的实例,不是旋转的是( )
A.传送带传送货物
B.螺旋桨的运动
C.风车风轮的运动
D.自行车车轮的运动
【分析】根据旋转的定义来判断:旋转就是将图形绕某点转动一定的角度,旋转后所得图形与原图形的形状、大小不变,对应点与旋转中心的连线的夹角相等.
【解答】解:传送带传送货物的过程中没有发生旋转.
故选:A.
【点评】本题考查了旋转,正确理解旋转的定义是解题的关键.
4.(2016 兰州)如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.πcm
B.2πcm
C.3πcm
D.5πcm
【分析】根据定滑轮的性质得到重物上升的即为转过的弧长,利用弧长公式计算即可.
【解答】解:根据题意得:l==3πcm,
则重物上升了3πcm,
故选C
【点评】此题考查了旋转的性质,以及弧长公式,熟练掌握旋转的性质是解本题的关键.
5.(2016 道外区二模)下列图形中,旋转对称图形有( )个.
A.1
B.2
C.3
D.4
【分析】根据旋转对称图形的定义对四个图形进行分析即可.
【解答】解:旋转对称图形是从左起第(1),(2),(4);不是旋转对称图形的是(3).
故选:C.
【点评】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
6.(2016春 南安市期末)下列现象中,不属于旋转的是( )
A.汽车在笔直的公路上行驶
B.大风车的转动
C.电风扇叶片的转动
D.时针的转动
【分析】根据旋转的定义分析求解.
【解答】解:因为在平面内,把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转,而汽车在笔直的公路上行驶是一种复合运动,车轮在旋转的同时又在作平移运动,
所以汽车在笔直的公路上行驶不属于旋转.
故:选A
【点评】本题考查了生活中的旋转现象;旋转是围绕一点旋转一定的角度的图形变换,因而旋转一定有旋转中心和旋转角,且旋转前后图形能够重合,这时判断旋转的关键
7.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
【分析】根据旋转的性质,△AOB绕点O旋转180°得到△DOE,点A与点D、B与E关于点O成中心对称解答.
【解答】解:∵△AOB绕点O旋转180°得到△DOE,
∴作图正确是C选项图形.
故选C.
【点评】本题考查了利用旋转变换作图,熟记旋转的性质,判断出对应点关于点O对称是解题的关键.
8.(2016春 巨野县期末)下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
A.
B.
C.
D.
【分析】分别根据旋转的定义及平移的定义逐项分析即可.
【解答】解:
A、B、C、D四个选项中的图形都可以看成是图形的一半旋转180°得到,
若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,
故A、B、D不能由平移得到,只有C选项的图形,可看成是由基本图形通过平移得到,
故选C.
【点评】本题主要考查旋转和平移的定义,掌握平移和旋转的特征是解题的关键.
9.(2015 武威校级模拟)观察图,在下列四种图形变换中,该图案不包含的变换是( )
A.旋转
B.轴对称
C.位似
D.平移
【分析】根据平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是一个图形沿一条直线对着直线两旁的部分能完全重合,位似是相似图形的每组对应点所在的直线都经过同一个点,可得答案.
【解答】解:A、大小相同的图形是旋转得到的,故A正确;
B、一个图形沿一条直线对着直线两旁的部分能完全重合,故B正确;
C、位置相同、形状相同的图案、大小不同的图形是位似得到的,故C正确;
D、图形没有平移,故D错误;
故选:D.
【点评】本题考查了几何变换的类型,平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,轴对称是一个图形沿一条直线对着直线两旁的部分能完全重合,位似是相似图形的每组对应点所在的直线都经过同一个点,观察时要紧扣图形变换特点,认真判断.
10.(2016 江西模拟)如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
A.(a﹣3,b)
B.(a+3,b)
C.(3﹣a,﹣b)
D.(a﹣3,﹣b)
【分析】先根据图形确定出对称中心,然后根据中点公式列式计算即可得解.
【解答】解:由图可知,△ABC与△A′B′C′关于点(1.5,0)成中心对称,
设点P′的坐标为(x,y),
所以,=1.5,=0,
解得x=3﹣a,y=﹣b,
所以,P′(3﹣a,﹣b).
故选:C.
【点评】本题考查了坐标与图形变化﹣旋转,准确识图,观察出两三角形成中心对称,对称中心是(1.5,0)是解题的关键.
二.填空题(共4小题)
11.(2016春 新化县期末)钟表的分针匀速旋转一周需要60min,经过20min,分针旋转了 120° .
【分析】钟表的分针匀速旋转一周需要60分,分针旋转了360°;求经过20分,分针的旋转度数,列出算式,解答出即可.
【解答】解:根据题意得,×360°=120°.
故答案为:120°.
【点评】本题考查了生活中的旋转现象,明确分针旋转一周,分针旋转了360°是解答本题的关键.
12.(2015 江西校级模拟)如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为 105° .
【分析】连结AC并且延长至E,根据旋转的性质和平角的定义,由角的和差关系即可求解.
【解答】解:如图:连结AC并且延长至E,
∠DCE=180°﹣∠DCB﹣∠ACB=105°.
故灰斗柄AB绕点C转动的角度为105°.
故答案为:105°.
【点评】考查了生活中的旋转现象,本题关键是由角的和差关系得到∠DCE的度数.
13.(2015春 印江县期末)如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是 (4) (在下列各图中选填正确图形的序号即可)
【分析】观察图形变化,图形(1)以点O为旋转中心,每次顺时针旋转90°,且每4次一个循环,由于2015=503×4+3,则第2015次旋转后的图形与(4)一样.
【解答】解:观察图形,将图形(1)以点O为旋转中心,每次顺时针旋转90°,得到下一个图形,每旋转四次回到原来的位置,
而2015=503×4+3,
所以第2015次旋转后的图形与(4)一样.
故答案为(4).
【点评】本题考查了生活中的旋转现象:在平面内,把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的角叫做旋转角.可以通过旋转得到很大美丽的图案.
14.(2016 南通)如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF= 2+ cm.
【分析】过点E作EM⊥BD于点M,则△DEM为等腰直角三角形,根据角平分线以及等腰直角三角形的性质即可得出DE的长度,再根据正方形以及旋转的性质即可得出线段BF的长.
【解答】解:过点E作EM⊥BD于点M,如图所示.
∵四边形ABCD为正方形,
∴∠BAC=45°,∠BCD=90°,
∴△DEM为等腰直角三角形.
∵BE平分∠DBC,EM⊥BD,
∴EM=EC=1cm,
∴DE=EM=cm.
由旋转的性质可知:CF=CE=1cm,
∴BF=BC+CF=CE+DE+CF=1++1=2+cm.
故答案为:2+.
【点评】本题考查了旋转的性质、正方形的性质以及角平分线的性质,解题的关键是求出线段BC以及CF的长度.本题属于基础题,难度不大,解决该题型题目时,结合角平分线以及等腰直角三角形的性质求出线段的长度是关键.
三.解答题(共6小题)
15.(2016 宁夏)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣1),B(3,﹣3),C(0,﹣4)
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
【分析】(1)根据网格结构找出点A、B、C关于原点对称的点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A1、B1、C1关于y轴对称的点A2、B2、C2的位置,然后顺次连接即可.
【解答】解:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示.
【点评】本题考查了利用旋转变换作图,利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
16.(2006 福州)(1)计算:+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 5 个;第2008个图案是 .
【分析】(1)根据绝对值,二次根式的性质化简原式,可得答案;
(2)分析可得,图形三个一组,且依次循环;10除3的余数为1,2008除3的余数为1,故第10个图案与第2008个图案相同,都是第一个图案,即;在前16个图案中有共5组,第六组只有第一个图案;故在前16个图案中有5个.
【解答】解:(1)原式==2;
(2)根据分析,知应分别为,5,.
【点评】本题考查代数式的化简及根据图形找规律的方法.
17.(2016春 临沂期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
【分析】(1)根据图形即可直接写出坐标;
(2)根据(1)中得到的横纵坐标之间的关系可以列方程求解;
(3)转化为图形的面积的和、差即可求解.
【解答】解:(1)A(2,3)与D(﹣2,﹣3);B(1,2)与E(﹣1,﹣2);C(3,1)与F(﹣3,﹣1).
对应点的坐标的特征:横坐标互为相反数,纵坐标互为相反数;
(2)由(1)可得a+3=﹣2a,4﹣b=﹣(2b﹣3).解得a=﹣1,b=﹣1;
(3)三角形ABC的面积=2×2﹣×2×1﹣×2×1﹣×1×1=.
【点评】本题考查了图形的中心对称变换,写出点的坐标得到对称的点之间的关系是关键.
18.(2016 瓯海区一模)如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和D,画△AOC和△BOD,使这两个三角形全等.
(1)在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形.
(2)在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.
【分析】(1)直接利用轴对称图形的性质得出符合题意的答案;
(2)直接利用旋转的性质得出符合题意的答案.
【解答】解:(1)如图1所示:△ACO,△DOB即为所求;
(2)如图2所示:△ACO,△DOB即为所求.
【点评】此题主要考查了轴对称变换以及旋转变换,正确得出对应点位置是解题关键.
19.(2016 常州一模)图l、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.请在网格中按照下列要求画出图形:
(1)在图1中以AB为边作四边形ABCD(点C、D在小正方形的顶点上),使得四边形ABCD为中心对称图形,且△ABD为轴对称图形(画出一个即可);
(2)在图2中以AB为边作四边形ABEF(点E、F在小正方形的顶点上),使得四边形ABEF中心对称图形但不是轴对称图形,且tan∠FAB=3.
【分析】(1)根据轴对称图形以及中心对称图形的性质得出符合题意的图形即可;
(2)利用轴对称图形以及中心对称图形的性质,再利用锐角三角函数关系得出答案.
【解答】解:(1)如图1所示:
(2)如图2所示.
【点评】此题主要考查了旋转变换以及轴对称变换,正确把握锐角三角函数关系是解题关键.
20.(2016 毕节市)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
【分析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是菱形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为等腰直角三角形,求出BD的长,由BD﹣DF求出BF的长即可.
【解答】解:(1)由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS);
(2)∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:AB=AD,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴BD2=2AB2,即BD=2,
∴AD=DF=FC=AC=AB=2,
∴BF=BD﹣DF=2﹣2.
【点评】此题考查了旋转的性质,全等三角形的判定与性质,以及菱形的性质,熟练掌握旋转的性质是解本题的关键.
第1页(共1页)
