黑龙江省双鸭山市友谊县红兴隆管理局一中2015-2016学年高二(下)开学数学试卷(理科)(解析版)
文档属性
| 名称 | 黑龙江省双鸭山市友谊县红兴隆管理局一中2015-2016学年高二(下)开学数学试卷(理科)(解析版) | 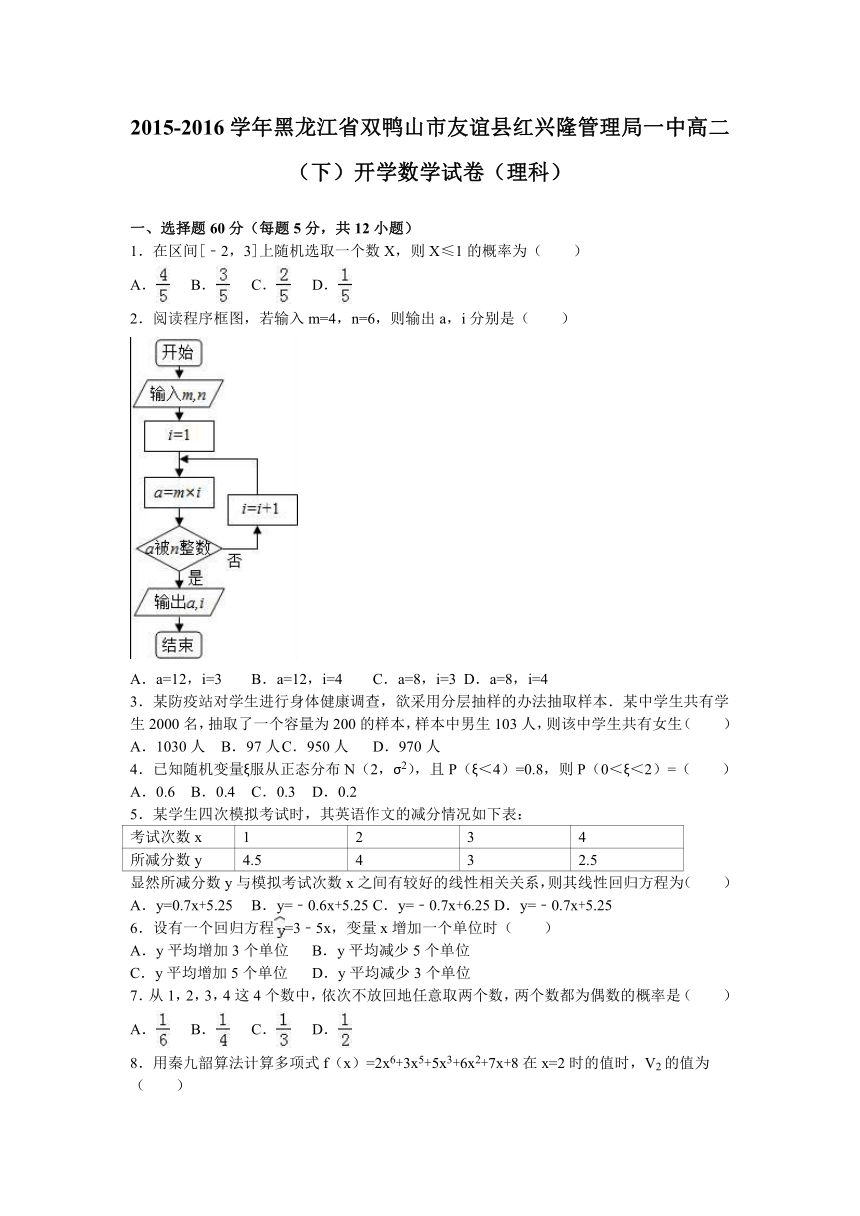 | |
| 格式 | zip | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 16:08:01 | ||
图片预览





文档简介
2015-2016学年黑龙江省双鸭山市友谊县红兴隆管理局一中高二(下)开学数学试卷(理科)
一、选择题60分(每题5分,共12小题)
1.在区间[﹣2,3]上随机选取一个数X,则X≤1的概率为( )
A.
B.
C.
D.
2.阅读程序框图,若输入m=4,n=6,则输出a,i分别是( )
A.a=12,i=3
B.a=12,i=4
C.a=8,i=3
D.a=8,i=4
3.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学生共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学生共有女生( )
A.1030人
B.97人
C.950人
D.970人
4.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
A.0.6
B.0.4
C.0.3
D.0.2
5.某学生四次模拟考试时,其英语作文的减分情况如下表:
考试次数x
1
2
3
4
所减分数y
4.5
4
3
2.5
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为( )
A.y=0.7x+5.25
B.y=﹣0.6x+5.25
C.y=﹣0.7x+6.25
D.y=﹣0.7x+5.25
6.设有一个回归方程=3﹣5x,变量x增加一个单位时( )
A.y平均增加3个单位
B.y平均减少5个单位
C.y平均增加5个单位
D.y平均减少3个单位
7.从1,2,3,4这4个数中,依次不放回地任意取两个数,两个数都为偶数的概率是( )
A.
B.
C.
D.
8.用秦九韶算法计算多项式f(x)=2x6+3x5+5x3+6x2+7x+8在x=2时的值时,V2的值为( )
A.2
B.19
C.14
D.33
9.盒子里有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是白球,则它是黑球的概率为( )
A.
B.
C.
D.
10.若(x6)n的展开式中含有常数项,则n的最小值等于( )
A.3
B.4
C.5
D.6
11.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0或2x+y﹣5=0
B.2x+y+=0或2x+y﹣=0
C.2x﹣y+5=0或2x﹣y﹣5=0
D.2x﹣y+=0或2x﹣y﹣=0
12.8个人坐成一排,现要调换其中3个人中每一个人的位置,其余5个人的位置不变,则不同的调换方式有( )
A.C83
B.C83A83
C.C83A22
D.3C83
二、填空题20分(每题5分,共4小题)
13.(x﹣2)(x﹣1)5的展开式中所有项的系数和等于______.
14.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,
3x4﹣2,3x5﹣2的平均数和方差分别是______.
15.在A,B两个袋中都有6张分别写有数字0,1,2,3,4,5的卡片,现从每个袋中任取一张卡片,两张卡片上的数字之和为X,则P(X=7)=______.
16.若直线y=x+b与曲线y=3﹣有公共点,则b的取值范围是______.
三、解答题70分
17.已知展开式中,第五项的二项式系数与第三项的二项式系数的比是14:3.
(1)求n.
(2)求含x2项的系数.
(3)求展开式中所有有理项.
18.已知曲线方程C:x2+y2﹣2x﹣4y+m=0.
(1)当m=﹣6时,求圆心和半径;
(2)若曲线C表示的圆与直线l:x+2y﹣4=0相交于M,N,且,求m的值.
19.连锁经营公司所属5个零售店某月的销售额利润资料如表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
(参考公式:
==,
=﹣x)
20.2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价
35岁以下人数
[2,4)
2
[4,6)
8
[6,8)
12
[8,10)
5
[10,12]
3
21.某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持
反对
总计
男生
30
女生
25
总计
(I)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(皿)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2=P(K2≥k0)
0.10
0.050
0.010
0.005
0.001
k0
2.706%
3.841
6.635
7.879
10.828
22.某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
(Ⅰ)分别计算两组数据的平均数,并比较哪个班级的客观题平均成绩更好;
(Ⅱ)从这两组数据各取两个数据,求其中至少有2个满分的概率;
(Ⅲ)规定客观题成绩不低于55分为“优秀客观卷”,以这20人的样本数据来估计此次高三数学模拟的总体数据,若从总体中任选4人,记X表示抽到“优秀客观卷”的学生人数,求X的分布列及数学期望.
2015-2016学年黑龙江省双鸭山市友谊县红兴隆管理局一中高二(下)开学数学试卷(理科)
参考答案与试题解析
一、选择题60分(每题5分,共12小题)
1.在区间[﹣2,3]上随机选取一个数X,则X≤1的概率为( )
A.
B.
C.
D.
【考点】几何概型.
【分析】利用几何槪型的概率公式,求出对应的区间长度,即可得到结论.
【解答】解:在区间[﹣2,3]上随机选取一个数X,
则﹣2≤X≤3,
则X≤1的概率P=,
故选:B.
2.阅读程序框图,若输入m=4,n=6,则输出a,i分别是( )
A.a=12,i=3
B.a=12,i=4
C.a=8,i=3
D.a=8,i=4
【考点】程序框图.
【分析】由程序框图依次计算第一、第二、第三次运行的结果,直到满足条件满足a被6整除,结束运行,输出此时a、i的值.
【解答】解:由程序框图得:
第一次运行i=1,a=4;
第二次运行i=2,a=8;
第三次运行i=3,a=12;满足a被6整除,结束运行,输出a=12,i=3.
故选A.
3.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学生共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学生共有女生( )
A.1030人
B.97人
C.950人
D.970人
【考点】分层抽样方法.
【分析】根据样本容量和女生比男生少6人,可得样本中女生数,再根据抽取的比例可得总体中的女生人数.
【解答】解:∵样本容量为200,女生比男生少6人,
∴样本中女生数为97人,
又分层抽样的抽取比例为=,
∴总体中女生数为970人.
故选:D.
4.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
A.0.6
B.0.4
C.0.3
D.0.2
【考点】正态分布曲线的特点及曲线所表示的意义.
【分析】根据随机变量X服从正态分布N(2,σ2),看出这组数据对应的正态曲线的对称轴x=2,根据正态曲线的特点,得到P(0<ξ<2)=P(0<ξ<4),得到结果.
【解答】解:∵随机变量X服从正态分布N(2,σ2),
μ=2,得对称轴是x=2.
P(ξ<4)=0.8
∴P(ξ≥4)=P(ξ≤0)=0.2,
∴P(0<ξ<4)=0.6
∴P(0<ξ<2)=0.3.
故选C.
5.某学生四次模拟考试时,其英语作文的减分情况如下表:
考试次数x
1
2
3
4
所减分数y
4.5
4
3
2.5
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为( )
A.y=0.7x+5.25
B.y=﹣0.6x+5.25
C.y=﹣0.7x+6.25
D.y=﹣0.7x+5.25
【考点】回归分析的初步应用.
【分析】先求样本中心点,利用线性回归方程一定过样本中心点,代入验证,可得结论.
【解答】解:先求样本中心点,,
由于线性回归方程一定过样本中心点,代入验证可知y=﹣0.7x+5.25,满足题意
故选D.
6.设有一个回归方程=3﹣5x,变量x增加一个单位时( )
A.y平均增加3个单位
B.y平均减少5个单位
C.y平均增加5个单位
D.y平均减少3个单位
【考点】线性回归方程.
【分析】回归方程=3﹣5x,变量x增加一个单位时,变量平均变化[3﹣5(x+1)]﹣(3﹣5x),及变量平均减少5个单位,得到结果.
【解答】解:∵﹣5是斜率的估计值,说明x每增加一个单位,y平均减少5个单位.
故选B
7.从1,2,3,4这4个数中,依次不放回地任意取两个数,两个数都为偶数的概率是( )
A.
B.
C.
D.
【考点】古典概型及其概率计算公式.
【分析】根据已知中从1,2,3,4这4个数中,不放回地任意取两个数,我们列出所有的基本事件个数,及满足条件两个数都是偶数的基本事件个数,代入古典概型概率公式,即可得到答案.
【解答】解:从1,2,3,4这4个数中,不放回地任意取两个数,共有
(1,2),(1,3),(1,4),(2,1),(2,3),(2,4)
(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种
其中满足条件两个数都是偶数的有(2,4),(4,2)两种情况
故从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率P=
故答案为
A
8.用秦九韶算法计算多项式f(x)=2x6+3x5+5x3+6x2+7x+8在x=2时的值时,V2的值为( )
A.2
B.19
C.14
D.33
【考点】秦九韶算法.
【分析】首先把一个n次多项式f(x)写成(…((anx+a
n﹣1)x+an﹣2)x+…+a1)x+a0的形式,然后化简,求n次多项式f(x)的值就转化为求n个一次多项式的值,求出V2的值.
【解答】解:∵f(x)=2x6+3x5+5x3+6x2+7x+8
=(((((2x+3)x+0)x+5)x+6)x+7)x+8
∴v0=a6=2,
v1=v0x+a5=2×2+3=7,
v2=v1x+a4=7×2+0=14,
故选C.
9.盒子里有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是白球,则它是黑球的概率为( )
A.
B.
C.
D.
【考点】等可能事件的概率.
【分析】本题是一个等可能事件的概率,试验发生包含的事件是从盒子中取出一个不是白球的小球,共有5+10=15种结果,满足条件的事件是取出的球是一个黑球,共有10种结果,得到概率.
【解答】解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从盒子中取出一个不是白球的小球,共有5+10=15种结果,
满足条件的事件是取出的球是一个黑球,共有10种结果,
∴根据等可能事件的概率得到P=
故选D.
10.若(x6)n的展开式中含有常数项,则n的最小值等于( )
A.3
B.4
C.5
D.6
【考点】二项式系数的性质.
【分析】二项式的通项公式Tr+1=Cnr(x6)n﹣r()r,对其进行整理,令x的指数为0,建立方程求出n的最小值.
【解答】解:由题意,(x6)n的展开式的项为Tr+1=Cnr(x6)n﹣r()r=Cnr=Cnr
令6n﹣r=0,得n=r,当r=4时,n取到最小值5
故选:C.
11.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0或2x+y﹣5=0
B.2x+y+=0或2x+y﹣=0
C.2x﹣y+5=0或2x﹣y﹣5=0
D.2x﹣y+=0或2x﹣y﹣=0
【考点】圆的切线方程.
【分析】设出所求直线方程,利用圆心到直线的距离等于半径,求出直线方程中的变量,即可求出直线方程.
【解答】解:设所求直线方程为2x+y+b=0,则,
所以=,所以b=±5,
所以所求直线方程为:2x+y+5=0或2x+y﹣5=0
故选:A.
12.8个人坐成一排,现要调换其中3个人中每一个人的位置,其余5个人的位置不变,则不同的调换方式有( )
A.C83
B.C83A83
C.C83A22
D.3C83
【考点】排列、组合的实际应用.
【分析】先考虑从8人中任选3人的方法数,再考虑3人位置全调的方法数,利用分步计数原理可求.
【解答】解:从8人中任选3人有C83种,3人位置全调,由于不能是自己原来的位置,因此有A22种,故有C83A22种.
故选C.
二、填空题20分(每题5分,共4小题)
13.(x﹣2)(x﹣1)5的展开式中所有项的系数和等于 0 .
【考点】二项式系数的性质.
【分析】令x=1,即可得到展开式中所有项的系数之和.
【解答】解:在(x﹣2)(x﹣1)5的展开式中,令x=1,
即(1﹣2)(1﹣1)5=0,
所以展开式中所有项的系数和等于0.
故答案为:0.
14.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,
3x4﹣2,3x5﹣2的平均数和方差分别是 4,3 .
【考点】极差、方差与标准差.
【分析】利用数据的平均数和方差的性质及计算公式直接求解.
【解答】解:∵一组数据x1,x2,x3,x4,x5的平均数是2,方差是,
∴另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数=3×2﹣2=4,
方差S2==3.
∴另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是4,3.
故答案为:4,3.
15.在A,B两个袋中都有6张分别写有数字0,1,2,3,4,5的卡片,现从每个袋中任取一张卡片,两张卡片上的数字之和为X,则P(X=7)= .
【考点】古典概型及其概率计算公式.
【分析】先求出基本事件总数n=6×6=36,再利用列举法求出X=7包含的基本事件个数,由此能求出P(X=7).
【解答】解:在A,B两个袋中都有6张分别写有数字0,1,2,3,4,5的卡片,
现从每个袋中任取一张卡片,两张卡片上的数字之和为X,
基本事件总数n=6×6=36,
X=7包含的基本事件有:(2,5),(5,2),(3,4),(4,3),共有m=4个,
∴P(X=7)==.
故答案为:.
16.若直线y=x+b与曲线y=3﹣有公共点,则b的取值范围是 [1﹣,3] .
【考点】直线与圆的位置关系.
【分析】曲线即
(x﹣2)2+(y﹣3)2=4(1≤y≤3),表示以A(2,3)为圆心,以2为半径的一个半圆,由圆心到直线y=x+b的距离等于半径2,解得
b=1+
b=1﹣.结合图象可得b的范围.
【解答】解:如图所示:曲线y=3﹣,即
(x﹣2)2+(y﹣3)2=4(
1≤y≤3,0≤x≤4),
表示以A(2,3)为圆心,以2为半径的一个半圆.
由圆心到直线y=x+b的距离等于半径2,可得=2,∴b=1+,或b=1﹣.
结合图象可得1﹣≤b≤3,
故答案为:[1﹣,3].
三、解答题70分
17.已知展开式中,第五项的二项式系数与第三项的二项式系数的比是14:3.
(1)求n.
(2)求含x2项的系数.
(3)求展开式中所有有理项.
【考点】二项式系数的性质.
【分析】(1)由题意可得=,由此求得n的值.
(2)在的开式的通项公式中,令x的幂指数等于2,求得r的值,可得含x2项的系数.
(3)根据∈z,r∈N,0≤r≤10,可得r=2,5,8,从而求得展开式中的有理项.
【解答】解:(1)由题意可得===,解得n=10.
(2)由于=,它的开式的通项公式为
Tr+1= ,
令=2,求得r=2,∴含x2项的系数为.
(3)根据∈z,r∈N,0≤r≤10,可得r=2,5,8,故第3、6、9项是有理项,
即有理项分别为、、.
18.已知曲线方程C:x2+y2﹣2x﹣4y+m=0.
(1)当m=﹣6时,求圆心和半径;
(2)若曲线C表示的圆与直线l:x+2y﹣4=0相交于M,N,且,求m的值.
【考点】直线与圆的位置关系.
【分析】(1)当m=﹣6时,方程C:x2+y2﹣2x﹣4y+m=0,可化为(x﹣1)2+(y﹣2)2=11,即可求得圆心和半径;
(2)利用圆心(1,2)到直线l:x+2y﹣4=0的距离公式可求得圆心到直线距离d,利用圆的半径、弦长之半、d构成的直角三角形即可求得m的值.
【解答】解:(1)当m=﹣6时,方程C:x2+y2﹣2x﹣4y+m=0,可化为(x﹣1)2+(y﹣2)2=11,
圆心坐标为(1,2),半径为;
(2)∵(x﹣1)2+(y﹣2)2=5﹣m,
∴圆心(1,2)到直线l:x+2y﹣4=0的距离d=,
又圆(x﹣1)2+(y﹣2)2=5﹣m的半径r=,,
∴()2+()2=5﹣m,得m=4.
19.连锁经营公司所属5个零售店某月的销售额利润资料如表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
(参考公式:
==,
=﹣x)
【考点】线性回归方程.
【分析】(1)根据表中所给的数对,在平面直角坐标系中画出散点图即可;
(2)求出对应的数值、以及n、xiyi、和n,代入公式即可求出回归直线方程的系数与方程;
(3)根据题意,令=10,求出x的值即可.
【解答】解:(1)根据表中所给的五对数对,在平面直角坐标系中画出散点图,
如图所示;
(2)∵==6,
=,
∴n=5×6×=102,
xiyi=3×2+5×3+6×3+7×4+9×5=112,
=32+52+62+72+92=200,
n=5×62=180,
===0.5,
=﹣=﹣0.5×6==0.4,
∴利润额y对销售额x的回归直线方程是=0.5x+0.4
(3)根据题意,令=0.5x+0.4=10,
解得x=19.2(千万元),
∴销售额约为19.2千万元.
20.2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价
35岁以下人数
[2,4)
2
[4,6)
8
[6,8)
12
[8,10)
5
[10,12]
3
【考点】离散型随机变量的期望与方差;频率分布直方图;离散型随机变量及其分布列.
【分析】(Ⅰ)由题意得:0.04×2+a×2+0.2×2+0.06×2+0.04×2=1,由此能求出a;由频率分布直方图估计众数为7,说明在被调查的50人中,能接受最高票价为7元的人数比能接受最高票价为其他值得人数多.
(Ⅱ)由题意知,X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列及数学期望.
【解答】(本题满分13分)
(Ⅰ)由题意得:0.04×2+a×2+0.2×2+0.06×2+0.04×2=1,
解得a=0.16…
由频率分布直方图估计众数为7,…
说明在被调查的50人中,能接受最高票价为7元的人数比能接受最高票价为其他值得人数多.…
(Ⅱ)由题意知,
50名被调查者中:选择最高票价在[8,10)的人数为0.06×2×50=6人.
选择最高票价在[10,12]的人数为0.04×2×50=4人
…
故X的可能取值为0,1,2,…
,
,
…
所以,X的分布列为:
X
0
1
2
P
…
21.某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持
反对
总计
男生
30
女生
25
总计
(I)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(皿)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2=P(K2≥k0)
0.10
0.050
0.010
0.005
0.001
k0
2.706%
3.841
6.635
7.879
10.828
【考点】独立性检验.
【分析】(Ⅰ)利用所给数据,可以完成列联表;求出k0,与临界值比较,即可得出能否有99.9%的把握认为态度与性别有关;
(Ⅱ)确定基本事件的个数,根据概率公式,可得结论.
【解答】解:(Ⅰ)列联表如下:
支持
反对
总计
男生
30
50
80
女生
45
25
70
总计
75
75
150
计算得K2=≈10.714<10.828,
所以没有99.9%的把握认为态度与性别有关.…
(Ⅱ)随机抽取一男一女所有可能的情况有24种,其中恰有一人支持一人反对的可能情况有2×2+4×212种,所以概率为P=.…
22.某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
(Ⅰ)分别计算两组数据的平均数,并比较哪个班级的客观题平均成绩更好;
(Ⅱ)从这两组数据各取两个数据,求其中至少有2个满分的概率;
(Ⅲ)规定客观题成绩不低于55分为“优秀客观卷”,以这20人的样本数据来估计此次高三数学模拟的总体数据,若从总体中任选4人,记X表示抽到“优秀客观卷”的学生人数,求X的分布列及数学期望.
【考点】离散型随机变量的期望与方差;古典概型及其概率计算公式;离散型随机变量及其分布列.
【分析】(I)根据数据计算两组数据的平均数;
(Ⅱ)从这两组数据中分别抽取一个数据,求其中至少有2个满分的概率;
(Ⅲ),求出其概率,可得X的分布列及数学期望.
【解答】解:(I)甲、乙两组数据的平均数分别为51.5,49,
甲班的客观题平均成绩更好.
(II)设从这两组数据各取两个数据,至少有2个满分为事件A,
则P(A)==;
(III)X
0
1
2
3
4
P
(人)…
2016年10月5日
一、选择题60分(每题5分,共12小题)
1.在区间[﹣2,3]上随机选取一个数X,则X≤1的概率为( )
A.
B.
C.
D.
2.阅读程序框图,若输入m=4,n=6,则输出a,i分别是( )
A.a=12,i=3
B.a=12,i=4
C.a=8,i=3
D.a=8,i=4
3.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学生共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学生共有女生( )
A.1030人
B.97人
C.950人
D.970人
4.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
A.0.6
B.0.4
C.0.3
D.0.2
5.某学生四次模拟考试时,其英语作文的减分情况如下表:
考试次数x
1
2
3
4
所减分数y
4.5
4
3
2.5
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为( )
A.y=0.7x+5.25
B.y=﹣0.6x+5.25
C.y=﹣0.7x+6.25
D.y=﹣0.7x+5.25
6.设有一个回归方程=3﹣5x,变量x增加一个单位时( )
A.y平均增加3个单位
B.y平均减少5个单位
C.y平均增加5个单位
D.y平均减少3个单位
7.从1,2,3,4这4个数中,依次不放回地任意取两个数,两个数都为偶数的概率是( )
A.
B.
C.
D.
8.用秦九韶算法计算多项式f(x)=2x6+3x5+5x3+6x2+7x+8在x=2时的值时,V2的值为( )
A.2
B.19
C.14
D.33
9.盒子里有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是白球,则它是黑球的概率为( )
A.
B.
C.
D.
10.若(x6)n的展开式中含有常数项,则n的最小值等于( )
A.3
B.4
C.5
D.6
11.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0或2x+y﹣5=0
B.2x+y+=0或2x+y﹣=0
C.2x﹣y+5=0或2x﹣y﹣5=0
D.2x﹣y+=0或2x﹣y﹣=0
12.8个人坐成一排,现要调换其中3个人中每一个人的位置,其余5个人的位置不变,则不同的调换方式有( )
A.C83
B.C83A83
C.C83A22
D.3C83
二、填空题20分(每题5分,共4小题)
13.(x﹣2)(x﹣1)5的展开式中所有项的系数和等于______.
14.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,
3x4﹣2,3x5﹣2的平均数和方差分别是______.
15.在A,B两个袋中都有6张分别写有数字0,1,2,3,4,5的卡片,现从每个袋中任取一张卡片,两张卡片上的数字之和为X,则P(X=7)=______.
16.若直线y=x+b与曲线y=3﹣有公共点,则b的取值范围是______.
三、解答题70分
17.已知展开式中,第五项的二项式系数与第三项的二项式系数的比是14:3.
(1)求n.
(2)求含x2项的系数.
(3)求展开式中所有有理项.
18.已知曲线方程C:x2+y2﹣2x﹣4y+m=0.
(1)当m=﹣6时,求圆心和半径;
(2)若曲线C表示的圆与直线l:x+2y﹣4=0相交于M,N,且,求m的值.
19.连锁经营公司所属5个零售店某月的销售额利润资料如表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
(参考公式:
==,
=﹣x)
20.2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价
35岁以下人数
[2,4)
2
[4,6)
8
[6,8)
12
[8,10)
5
[10,12]
3
21.某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持
反对
总计
男生
30
女生
25
总计
(I)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(皿)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2=P(K2≥k0)
0.10
0.050
0.010
0.005
0.001
k0
2.706%
3.841
6.635
7.879
10.828
22.某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
(Ⅰ)分别计算两组数据的平均数,并比较哪个班级的客观题平均成绩更好;
(Ⅱ)从这两组数据各取两个数据,求其中至少有2个满分的概率;
(Ⅲ)规定客观题成绩不低于55分为“优秀客观卷”,以这20人的样本数据来估计此次高三数学模拟的总体数据,若从总体中任选4人,记X表示抽到“优秀客观卷”的学生人数,求X的分布列及数学期望.
2015-2016学年黑龙江省双鸭山市友谊县红兴隆管理局一中高二(下)开学数学试卷(理科)
参考答案与试题解析
一、选择题60分(每题5分,共12小题)
1.在区间[﹣2,3]上随机选取一个数X,则X≤1的概率为( )
A.
B.
C.
D.
【考点】几何概型.
【分析】利用几何槪型的概率公式,求出对应的区间长度,即可得到结论.
【解答】解:在区间[﹣2,3]上随机选取一个数X,
则﹣2≤X≤3,
则X≤1的概率P=,
故选:B.
2.阅读程序框图,若输入m=4,n=6,则输出a,i分别是( )
A.a=12,i=3
B.a=12,i=4
C.a=8,i=3
D.a=8,i=4
【考点】程序框图.
【分析】由程序框图依次计算第一、第二、第三次运行的结果,直到满足条件满足a被6整除,结束运行,输出此时a、i的值.
【解答】解:由程序框图得:
第一次运行i=1,a=4;
第二次运行i=2,a=8;
第三次运行i=3,a=12;满足a被6整除,结束运行,输出a=12,i=3.
故选A.
3.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学生共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学生共有女生( )
A.1030人
B.97人
C.950人
D.970人
【考点】分层抽样方法.
【分析】根据样本容量和女生比男生少6人,可得样本中女生数,再根据抽取的比例可得总体中的女生人数.
【解答】解:∵样本容量为200,女生比男生少6人,
∴样本中女生数为97人,
又分层抽样的抽取比例为=,
∴总体中女生数为970人.
故选:D.
4.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
A.0.6
B.0.4
C.0.3
D.0.2
【考点】正态分布曲线的特点及曲线所表示的意义.
【分析】根据随机变量X服从正态分布N(2,σ2),看出这组数据对应的正态曲线的对称轴x=2,根据正态曲线的特点,得到P(0<ξ<2)=P(0<ξ<4),得到结果.
【解答】解:∵随机变量X服从正态分布N(2,σ2),
μ=2,得对称轴是x=2.
P(ξ<4)=0.8
∴P(ξ≥4)=P(ξ≤0)=0.2,
∴P(0<ξ<4)=0.6
∴P(0<ξ<2)=0.3.
故选C.
5.某学生四次模拟考试时,其英语作文的减分情况如下表:
考试次数x
1
2
3
4
所减分数y
4.5
4
3
2.5
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为( )
A.y=0.7x+5.25
B.y=﹣0.6x+5.25
C.y=﹣0.7x+6.25
D.y=﹣0.7x+5.25
【考点】回归分析的初步应用.
【分析】先求样本中心点,利用线性回归方程一定过样本中心点,代入验证,可得结论.
【解答】解:先求样本中心点,,
由于线性回归方程一定过样本中心点,代入验证可知y=﹣0.7x+5.25,满足题意
故选D.
6.设有一个回归方程=3﹣5x,变量x增加一个单位时( )
A.y平均增加3个单位
B.y平均减少5个单位
C.y平均增加5个单位
D.y平均减少3个单位
【考点】线性回归方程.
【分析】回归方程=3﹣5x,变量x增加一个单位时,变量平均变化[3﹣5(x+1)]﹣(3﹣5x),及变量平均减少5个单位,得到结果.
【解答】解:∵﹣5是斜率的估计值,说明x每增加一个单位,y平均减少5个单位.
故选B
7.从1,2,3,4这4个数中,依次不放回地任意取两个数,两个数都为偶数的概率是( )
A.
B.
C.
D.
【考点】古典概型及其概率计算公式.
【分析】根据已知中从1,2,3,4这4个数中,不放回地任意取两个数,我们列出所有的基本事件个数,及满足条件两个数都是偶数的基本事件个数,代入古典概型概率公式,即可得到答案.
【解答】解:从1,2,3,4这4个数中,不放回地任意取两个数,共有
(1,2),(1,3),(1,4),(2,1),(2,3),(2,4)
(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种
其中满足条件两个数都是偶数的有(2,4),(4,2)两种情况
故从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率P=
故答案为
A
8.用秦九韶算法计算多项式f(x)=2x6+3x5+5x3+6x2+7x+8在x=2时的值时,V2的值为( )
A.2
B.19
C.14
D.33
【考点】秦九韶算法.
【分析】首先把一个n次多项式f(x)写成(…((anx+a
n﹣1)x+an﹣2)x+…+a1)x+a0的形式,然后化简,求n次多项式f(x)的值就转化为求n个一次多项式的值,求出V2的值.
【解答】解:∵f(x)=2x6+3x5+5x3+6x2+7x+8
=(((((2x+3)x+0)x+5)x+6)x+7)x+8
∴v0=a6=2,
v1=v0x+a5=2×2+3=7,
v2=v1x+a4=7×2+0=14,
故选C.
9.盒子里有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是白球,则它是黑球的概率为( )
A.
B.
C.
D.
【考点】等可能事件的概率.
【分析】本题是一个等可能事件的概率,试验发生包含的事件是从盒子中取出一个不是白球的小球,共有5+10=15种结果,满足条件的事件是取出的球是一个黑球,共有10种结果,得到概率.
【解答】解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从盒子中取出一个不是白球的小球,共有5+10=15种结果,
满足条件的事件是取出的球是一个黑球,共有10种结果,
∴根据等可能事件的概率得到P=
故选D.
10.若(x6)n的展开式中含有常数项,则n的最小值等于( )
A.3
B.4
C.5
D.6
【考点】二项式系数的性质.
【分析】二项式的通项公式Tr+1=Cnr(x6)n﹣r()r,对其进行整理,令x的指数为0,建立方程求出n的最小值.
【解答】解:由题意,(x6)n的展开式的项为Tr+1=Cnr(x6)n﹣r()r=Cnr=Cnr
令6n﹣r=0,得n=r,当r=4时,n取到最小值5
故选:C.
11.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0或2x+y﹣5=0
B.2x+y+=0或2x+y﹣=0
C.2x﹣y+5=0或2x﹣y﹣5=0
D.2x﹣y+=0或2x﹣y﹣=0
【考点】圆的切线方程.
【分析】设出所求直线方程,利用圆心到直线的距离等于半径,求出直线方程中的变量,即可求出直线方程.
【解答】解:设所求直线方程为2x+y+b=0,则,
所以=,所以b=±5,
所以所求直线方程为:2x+y+5=0或2x+y﹣5=0
故选:A.
12.8个人坐成一排,现要调换其中3个人中每一个人的位置,其余5个人的位置不变,则不同的调换方式有( )
A.C83
B.C83A83
C.C83A22
D.3C83
【考点】排列、组合的实际应用.
【分析】先考虑从8人中任选3人的方法数,再考虑3人位置全调的方法数,利用分步计数原理可求.
【解答】解:从8人中任选3人有C83种,3人位置全调,由于不能是自己原来的位置,因此有A22种,故有C83A22种.
故选C.
二、填空题20分(每题5分,共4小题)
13.(x﹣2)(x﹣1)5的展开式中所有项的系数和等于 0 .
【考点】二项式系数的性质.
【分析】令x=1,即可得到展开式中所有项的系数之和.
【解答】解:在(x﹣2)(x﹣1)5的展开式中,令x=1,
即(1﹣2)(1﹣1)5=0,
所以展开式中所有项的系数和等于0.
故答案为:0.
14.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,
3x4﹣2,3x5﹣2的平均数和方差分别是 4,3 .
【考点】极差、方差与标准差.
【分析】利用数据的平均数和方差的性质及计算公式直接求解.
【解答】解:∵一组数据x1,x2,x3,x4,x5的平均数是2,方差是,
∴另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数=3×2﹣2=4,
方差S2==3.
∴另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是4,3.
故答案为:4,3.
15.在A,B两个袋中都有6张分别写有数字0,1,2,3,4,5的卡片,现从每个袋中任取一张卡片,两张卡片上的数字之和为X,则P(X=7)= .
【考点】古典概型及其概率计算公式.
【分析】先求出基本事件总数n=6×6=36,再利用列举法求出X=7包含的基本事件个数,由此能求出P(X=7).
【解答】解:在A,B两个袋中都有6张分别写有数字0,1,2,3,4,5的卡片,
现从每个袋中任取一张卡片,两张卡片上的数字之和为X,
基本事件总数n=6×6=36,
X=7包含的基本事件有:(2,5),(5,2),(3,4),(4,3),共有m=4个,
∴P(X=7)==.
故答案为:.
16.若直线y=x+b与曲线y=3﹣有公共点,则b的取值范围是 [1﹣,3] .
【考点】直线与圆的位置关系.
【分析】曲线即
(x﹣2)2+(y﹣3)2=4(1≤y≤3),表示以A(2,3)为圆心,以2为半径的一个半圆,由圆心到直线y=x+b的距离等于半径2,解得
b=1+
b=1﹣.结合图象可得b的范围.
【解答】解:如图所示:曲线y=3﹣,即
(x﹣2)2+(y﹣3)2=4(
1≤y≤3,0≤x≤4),
表示以A(2,3)为圆心,以2为半径的一个半圆.
由圆心到直线y=x+b的距离等于半径2,可得=2,∴b=1+,或b=1﹣.
结合图象可得1﹣≤b≤3,
故答案为:[1﹣,3].
三、解答题70分
17.已知展开式中,第五项的二项式系数与第三项的二项式系数的比是14:3.
(1)求n.
(2)求含x2项的系数.
(3)求展开式中所有有理项.
【考点】二项式系数的性质.
【分析】(1)由题意可得=,由此求得n的值.
(2)在的开式的通项公式中,令x的幂指数等于2,求得r的值,可得含x2项的系数.
(3)根据∈z,r∈N,0≤r≤10,可得r=2,5,8,从而求得展开式中的有理项.
【解答】解:(1)由题意可得===,解得n=10.
(2)由于=,它的开式的通项公式为
Tr+1= ,
令=2,求得r=2,∴含x2项的系数为.
(3)根据∈z,r∈N,0≤r≤10,可得r=2,5,8,故第3、6、9项是有理项,
即有理项分别为、、.
18.已知曲线方程C:x2+y2﹣2x﹣4y+m=0.
(1)当m=﹣6时,求圆心和半径;
(2)若曲线C表示的圆与直线l:x+2y﹣4=0相交于M,N,且,求m的值.
【考点】直线与圆的位置关系.
【分析】(1)当m=﹣6时,方程C:x2+y2﹣2x﹣4y+m=0,可化为(x﹣1)2+(y﹣2)2=11,即可求得圆心和半径;
(2)利用圆心(1,2)到直线l:x+2y﹣4=0的距离公式可求得圆心到直线距离d,利用圆的半径、弦长之半、d构成的直角三角形即可求得m的值.
【解答】解:(1)当m=﹣6时,方程C:x2+y2﹣2x﹣4y+m=0,可化为(x﹣1)2+(y﹣2)2=11,
圆心坐标为(1,2),半径为;
(2)∵(x﹣1)2+(y﹣2)2=5﹣m,
∴圆心(1,2)到直线l:x+2y﹣4=0的距离d=,
又圆(x﹣1)2+(y﹣2)2=5﹣m的半径r=,,
∴()2+()2=5﹣m,得m=4.
19.连锁经营公司所属5个零售店某月的销售额利润资料如表:
商品名称
A
B
C
D
E
销售额x/千万元
3
5
6
7
9
利润额y/百万元
2
3
3
4
5
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
(参考公式:
==,
=﹣x)
【考点】线性回归方程.
【分析】(1)根据表中所给的数对,在平面直角坐标系中画出散点图即可;
(2)求出对应的数值、以及n、xiyi、和n,代入公式即可求出回归直线方程的系数与方程;
(3)根据题意,令=10,求出x的值即可.
【解答】解:(1)根据表中所给的五对数对,在平面直角坐标系中画出散点图,
如图所示;
(2)∵==6,
=,
∴n=5×6×=102,
xiyi=3×2+5×3+6×3+7×4+9×5=112,
=32+52+62+72+92=200,
n=5×62=180,
===0.5,
=﹣=﹣0.5×6==0.4,
∴利润额y对销售额x的回归直线方程是=0.5x+0.4
(3)根据题意,令=0.5x+0.4=10,
解得x=19.2(千万元),
∴销售额约为19.2千万元.
20.2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价
35岁以下人数
[2,4)
2
[4,6)
8
[6,8)
12
[8,10)
5
[10,12]
3
【考点】离散型随机变量的期望与方差;频率分布直方图;离散型随机变量及其分布列.
【分析】(Ⅰ)由题意得:0.04×2+a×2+0.2×2+0.06×2+0.04×2=1,由此能求出a;由频率分布直方图估计众数为7,说明在被调查的50人中,能接受最高票价为7元的人数比能接受最高票价为其他值得人数多.
(Ⅱ)由题意知,X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列及数学期望.
【解答】(本题满分13分)
(Ⅰ)由题意得:0.04×2+a×2+0.2×2+0.06×2+0.04×2=1,
解得a=0.16…
由频率分布直方图估计众数为7,…
说明在被调查的50人中,能接受最高票价为7元的人数比能接受最高票价为其他值得人数多.…
(Ⅱ)由题意知,
50名被调查者中:选择最高票价在[8,10)的人数为0.06×2×50=6人.
选择最高票价在[10,12]的人数为0.04×2×50=4人
…
故X的可能取值为0,1,2,…
,
,
…
所以,X的分布列为:
X
0
1
2
P
…
21.某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持
反对
总计
男生
30
女生
25
总计
(I)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(皿)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2=P(K2≥k0)
0.10
0.050
0.010
0.005
0.001
k0
2.706%
3.841
6.635
7.879
10.828
【考点】独立性检验.
【分析】(Ⅰ)利用所给数据,可以完成列联表;求出k0,与临界值比较,即可得出能否有99.9%的把握认为态度与性别有关;
(Ⅱ)确定基本事件的个数,根据概率公式,可得结论.
【解答】解:(Ⅰ)列联表如下:
支持
反对
总计
男生
30
50
80
女生
45
25
70
总计
75
75
150
计算得K2=≈10.714<10.828,
所以没有99.9%的把握认为态度与性别有关.…
(Ⅱ)随机抽取一男一女所有可能的情况有24种,其中恰有一人支持一人反对的可能情况有2×2+4×212种,所以概率为P=.…
22.某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
(Ⅰ)分别计算两组数据的平均数,并比较哪个班级的客观题平均成绩更好;
(Ⅱ)从这两组数据各取两个数据,求其中至少有2个满分的概率;
(Ⅲ)规定客观题成绩不低于55分为“优秀客观卷”,以这20人的样本数据来估计此次高三数学模拟的总体数据,若从总体中任选4人,记X表示抽到“优秀客观卷”的学生人数,求X的分布列及数学期望.
【考点】离散型随机变量的期望与方差;古典概型及其概率计算公式;离散型随机变量及其分布列.
【分析】(I)根据数据计算两组数据的平均数;
(Ⅱ)从这两组数据中分别抽取一个数据,求其中至少有2个满分的概率;
(Ⅲ),求出其概率,可得X的分布列及数学期望.
【解答】解:(I)甲、乙两组数据的平均数分别为51.5,49,
甲班的客观题平均成绩更好.
(II)设从这两组数据各取两个数据,至少有2个满分为事件A,
则P(A)==;
(III)X
0
1
2
3
4
P
(人)…
2016年10月5日
同课章节目录
