高中数学函数
图片预览


文档简介
函数
1.函数的定义
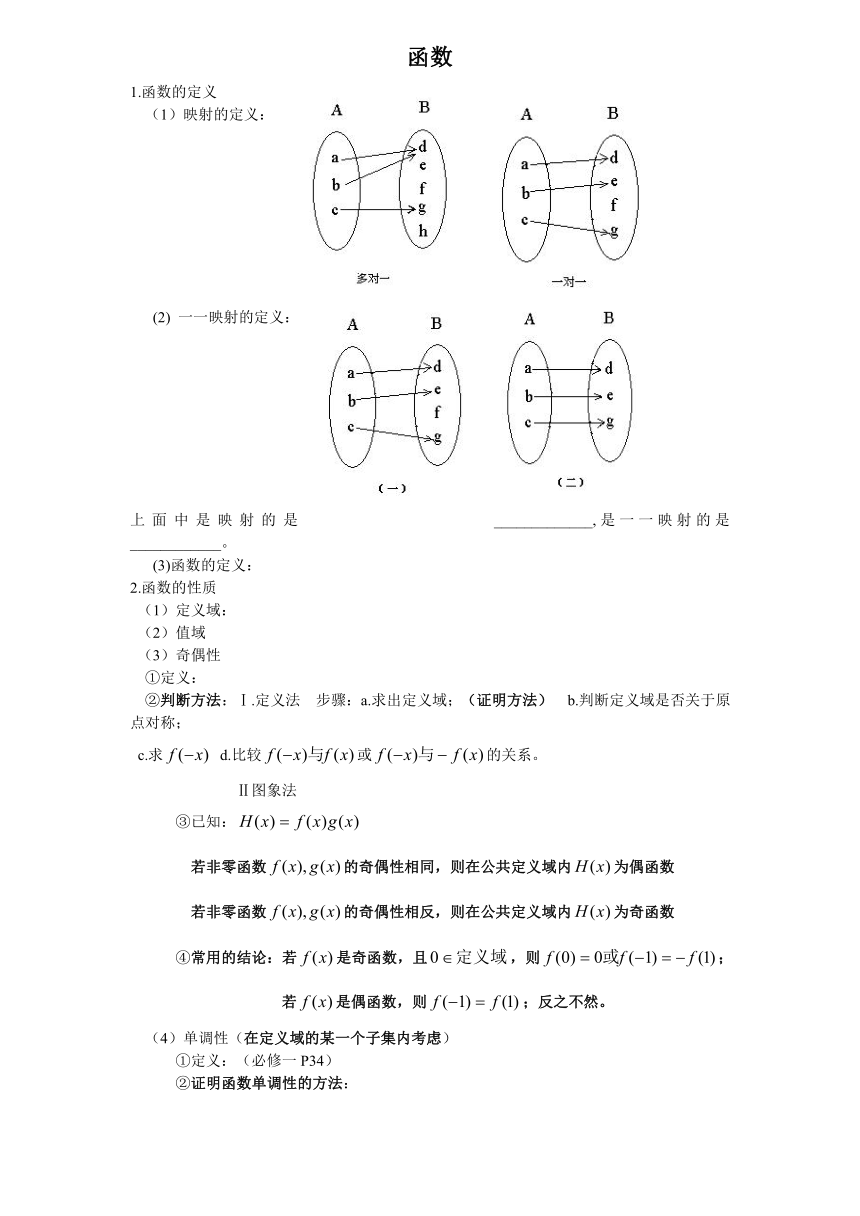
(1)映射的定义:
(2) 一一映射的定义:
上面中是映射的是_____________,是一一映射的是____________。
(3)函数的定义:
2.函数的性质
(1)定义域:
(2)值域
(3)奇偶性
①定义:
②判断方法:Ⅰ.定义法 步骤:a.求出定义域;(证明方法) b.判断定义域是否关于原点对称;
c.求 d.比较或的关系。
Ⅱ图象法
③已知:
若非零函数的奇偶性相同,则在公共定义域内为偶函数
若非零函数的奇偶性相反,则在公共定义域内为奇函数
④常用的结论:若是奇函数,且,则;
若是偶函数,则;反之不然。
(4)单调性(在定义域的某一个子集内考虑)
①定义:(必修一P34)
②证明函数单调性的方法:
Ⅰ.定义法 步骤:
a.设;
b.作差;
(一般结果要分解为若干个因式的乘积,且每一个因式的正或负号能清楚地判断出)
c.判断正负号。
Ⅱ用导数证明: 若在某个区间A内有导数,
则在A内为增函数;
在A内为减函数。
③求单调区间的方法:
a.定义法: b.导数法:c.图象法: d.复合函数在公共定义域上的单调性:
若f与g的单调性相同,则为增函数;
若f与g的单调性相反,则为减函数。
注意:先求定义域,单调区间是定义域的子集。
④一些有用的结论:
a.奇函数在其对称区间上的单调性相同;
b.偶函数在其对称区间上的单调性相反;
c.在公共定义域内
增函数增函数是增函数;
减函数减函数是减函数;
增函数减函数是增函数;
减函数增函数是减函数。
d.函数在上单调递增;在上
是单调递减。
(5)函数的周期性
定义:若T为非零常数,对于定义域内的任一x,使恒成立
则f(x)叫做周期函数,T叫做这个函数的一个周期。
例:(1)若函数在R上是奇函数,且在上是增函数,且
则①关于 对称;②的周期为 ;
③在(1,2)是 函数(增、减);
④=,则 。
(2)设是定义在上,以2为周期的周期函数,且为偶函数,在区间[2,3]上,=,则= 。
3、函数的图象
1、基本函数的图象:(1)一次函数、(2)二次函数、(3)反比例函数、(4)指数函数、(5)对数函数、(6)三角函数。
2、图象的变换
(1)平移变换
①函数的图象是把函数平;
②函数的图象是把函数右平;
③函数的图象是把函数平;
④函数的图象是把函数平。
(2)对称变换
①函数与函数的图象关于直线x=0对称;
函数与函数的图象关于直线y=0对称;
函数与函数的图象关于坐标原点对称;
②如果函数对于一切都有,那么 的图象关于直线对称。
③函数与函数的图象关于直线对称。
④
⑤
⑥与关于直线对称。
(3)伸缩变换
①的图象,可将的图象上的每一点的纵坐标伸长或缩短到原来的倍。
②的图象,可将的图象上的每一点的横坐标伸长或缩短到原来的倍。
例:(1)已知函数的图象过点(1,1),则的反函数的图象过点 。
(2)由函数的图象,通过怎样的变换得到的图象?
4、函数的反函数
1、求反函数的步骤:
①求原函数,的值域B
②把看作方程,解出;
③x,y互换的的反函数为,。
2、函数与反函数之间的一个有用的结论:
3、原函数在区间上单调递增,则一定存在反函数,且反函数也单调递增;但一个函数存在反函数,此函数不一定单调。
例1:,的反函数为 。
2:已知,求的反函数。
3:设 。
4:四十五分钟能力训练题十(13题)。
5、函数、方程与不等式
1、“实系数一元二次方程有实数解”转化为“”,你是否注意到必须;当=0时,“方程有解”不能转化为。若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?
2、利用二次函数的图象和性质,讨论一元二次方程实根的分布。
设为方程的两个实根。
①若则;
②当在区间内有且只有一个实根,时,
③当在区间内有且只有两个实根时,
④若时
注意:①根据要求先画出抛物线,然后写出图象成立的充要条件。
②注意端点,验证端点。
例:1、对于定义在R上的函数若其所以的函数值都不超过1,则m的取值范围 。
2、已知函数的定义域是一切实数,则 。
3、若关于x的方程有实根,则 。
4、设集合A=,B是关于x的不等式组的解集,试确定的取值范围,使。
5、已知方程的两个根为一个三角形两内角的正切值,试求的取值范围。
1.函数的定义
(1)映射的定义:
(2) 一一映射的定义:
上面中是映射的是_____________,是一一映射的是____________。
(3)函数的定义:
2.函数的性质
(1)定义域:
(2)值域
(3)奇偶性
①定义:
②判断方法:Ⅰ.定义法 步骤:a.求出定义域;(证明方法) b.判断定义域是否关于原点对称;
c.求 d.比较或的关系。
Ⅱ图象法
③已知:
若非零函数的奇偶性相同,则在公共定义域内为偶函数
若非零函数的奇偶性相反,则在公共定义域内为奇函数
④常用的结论:若是奇函数,且,则;
若是偶函数,则;反之不然。
(4)单调性(在定义域的某一个子集内考虑)
①定义:(必修一P34)
②证明函数单调性的方法:
Ⅰ.定义法 步骤:
a.设;
b.作差;
(一般结果要分解为若干个因式的乘积,且每一个因式的正或负号能清楚地判断出)
c.判断正负号。
Ⅱ用导数证明: 若在某个区间A内有导数,
则在A内为增函数;
在A内为减函数。
③求单调区间的方法:
a.定义法: b.导数法:c.图象法: d.复合函数在公共定义域上的单调性:
若f与g的单调性相同,则为增函数;
若f与g的单调性相反,则为减函数。
注意:先求定义域,单调区间是定义域的子集。
④一些有用的结论:
a.奇函数在其对称区间上的单调性相同;
b.偶函数在其对称区间上的单调性相反;
c.在公共定义域内
增函数增函数是增函数;
减函数减函数是减函数;
增函数减函数是增函数;
减函数增函数是减函数。
d.函数在上单调递增;在上
是单调递减。
(5)函数的周期性
定义:若T为非零常数,对于定义域内的任一x,使恒成立
则f(x)叫做周期函数,T叫做这个函数的一个周期。
例:(1)若函数在R上是奇函数,且在上是增函数,且
则①关于 对称;②的周期为 ;
③在(1,2)是 函数(增、减);
④=,则 。
(2)设是定义在上,以2为周期的周期函数,且为偶函数,在区间[2,3]上,=,则= 。
3、函数的图象
1、基本函数的图象:(1)一次函数、(2)二次函数、(3)反比例函数、(4)指数函数、(5)对数函数、(6)三角函数。
2、图象的变换
(1)平移变换
①函数的图象是把函数平;
②函数的图象是把函数右平;
③函数的图象是把函数平;
④函数的图象是把函数平。
(2)对称变换
①函数与函数的图象关于直线x=0对称;
函数与函数的图象关于直线y=0对称;
函数与函数的图象关于坐标原点对称;
②如果函数对于一切都有,那么 的图象关于直线对称。
③函数与函数的图象关于直线对称。
④
⑤
⑥与关于直线对称。
(3)伸缩变换
①的图象,可将的图象上的每一点的纵坐标伸长或缩短到原来的倍。
②的图象,可将的图象上的每一点的横坐标伸长或缩短到原来的倍。
例:(1)已知函数的图象过点(1,1),则的反函数的图象过点 。
(2)由函数的图象,通过怎样的变换得到的图象?
4、函数的反函数
1、求反函数的步骤:
①求原函数,的值域B
②把看作方程,解出;
③x,y互换的的反函数为,。
2、函数与反函数之间的一个有用的结论:
3、原函数在区间上单调递增,则一定存在反函数,且反函数也单调递增;但一个函数存在反函数,此函数不一定单调。
例1:,的反函数为 。
2:已知,求的反函数。
3:设 。
4:四十五分钟能力训练题十(13题)。
5、函数、方程与不等式
1、“实系数一元二次方程有实数解”转化为“”,你是否注意到必须;当=0时,“方程有解”不能转化为。若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?
2、利用二次函数的图象和性质,讨论一元二次方程实根的分布。
设为方程的两个实根。
①若则;
②当在区间内有且只有一个实根,时,
③当在区间内有且只有两个实根时,
④若时
注意:①根据要求先画出抛物线,然后写出图象成立的充要条件。
②注意端点,验证端点。
例:1、对于定义在R上的函数若其所以的函数值都不超过1,则m的取值范围 。
2、已知函数的定义域是一切实数,则 。
3、若关于x的方程有实根,则 。
4、设集合A=,B是关于x的不等式组的解集,试确定的取值范围,使。
5、已知方程的两个根为一个三角形两内角的正切值,试求的取值范围。
