沪科版九年级数学下册24.4.3切线长定理测试卷(解析版)
文档属性
| 名称 | 沪科版九年级数学下册24.4.3切线长定理测试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 15:46:57 | ||
图片预览


文档简介
沪科版九年级数学下册24.4.3《切线长定理》测试卷
一.选择题(共10小题)
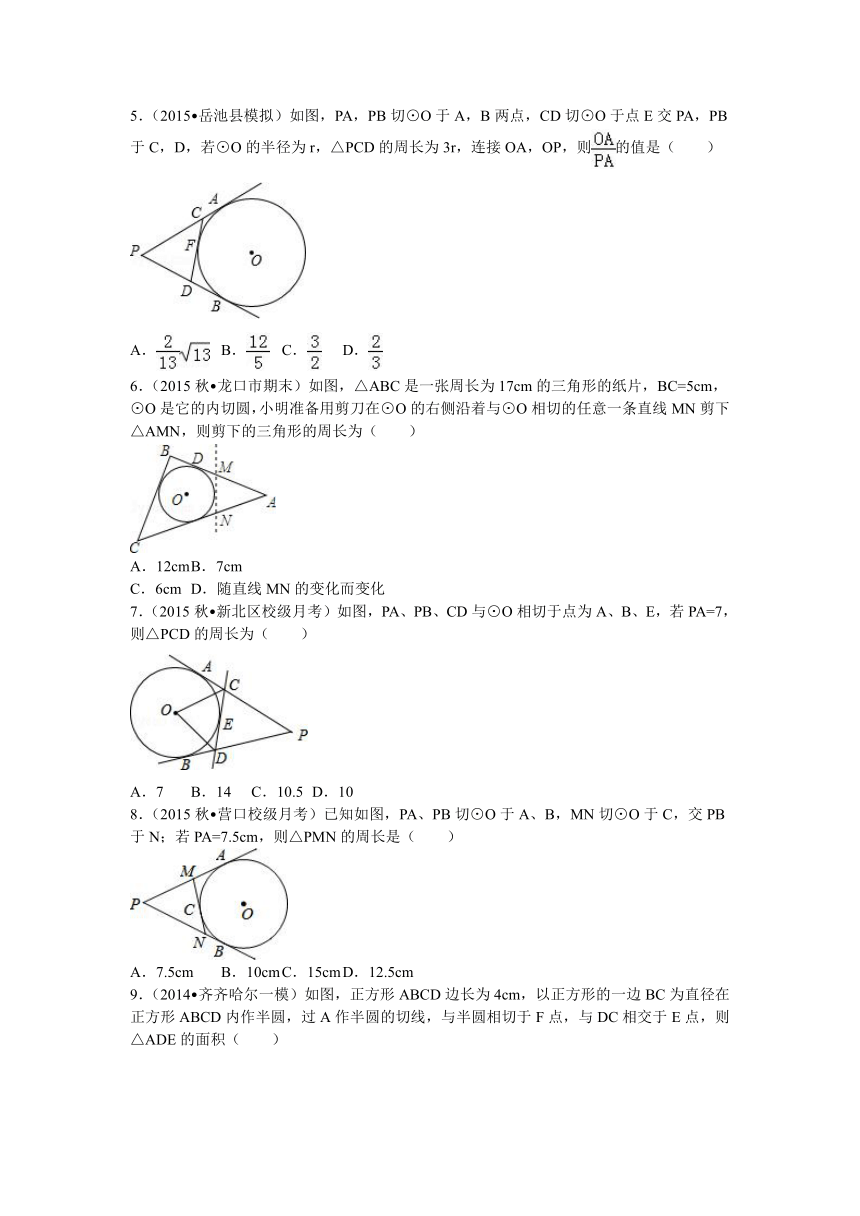
1.(2016 十堰二模)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2,则线段AB的长是( )
A.
B.3
C.2
D.3
2.(2016 曲靖一模)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
A.5
B.7
C.8
D.10
3.(2015 东西湖区校级模拟)如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O
切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
A.9
B.10
C.3
D.2
4.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( )
A.32
B.34
C.36
D.38
5.(2015 岳池县模拟)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是( )
A.
B.
C.
D.
6.(2015秋 龙口市期末)如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm
B.7cm
C.6cm
D.随直线MN的变化而变化
7.(2015秋 新北区校级月考)如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7
B.14
C.10.5
D.10
8.(2015秋 营口校级月考)已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.15cm
D.12.5cm
9.(2014 齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
10.(2014秋 德城区期末)如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm
B.15cm
C.10cm
D.随直线MN的变化而变化
二.填空题(共4小题)
11.(2016 丹阳市校级模拟)如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于______.
12.(2016春 合肥校级月考)如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是______.
13.(2016春 盘锦校级月考)如图,圆外切四边形ABCD,且AB=15,CD=9,则四边形的周长是______.
14.(2015 滨海县一模)如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为______.
三.解答题(共6小题)
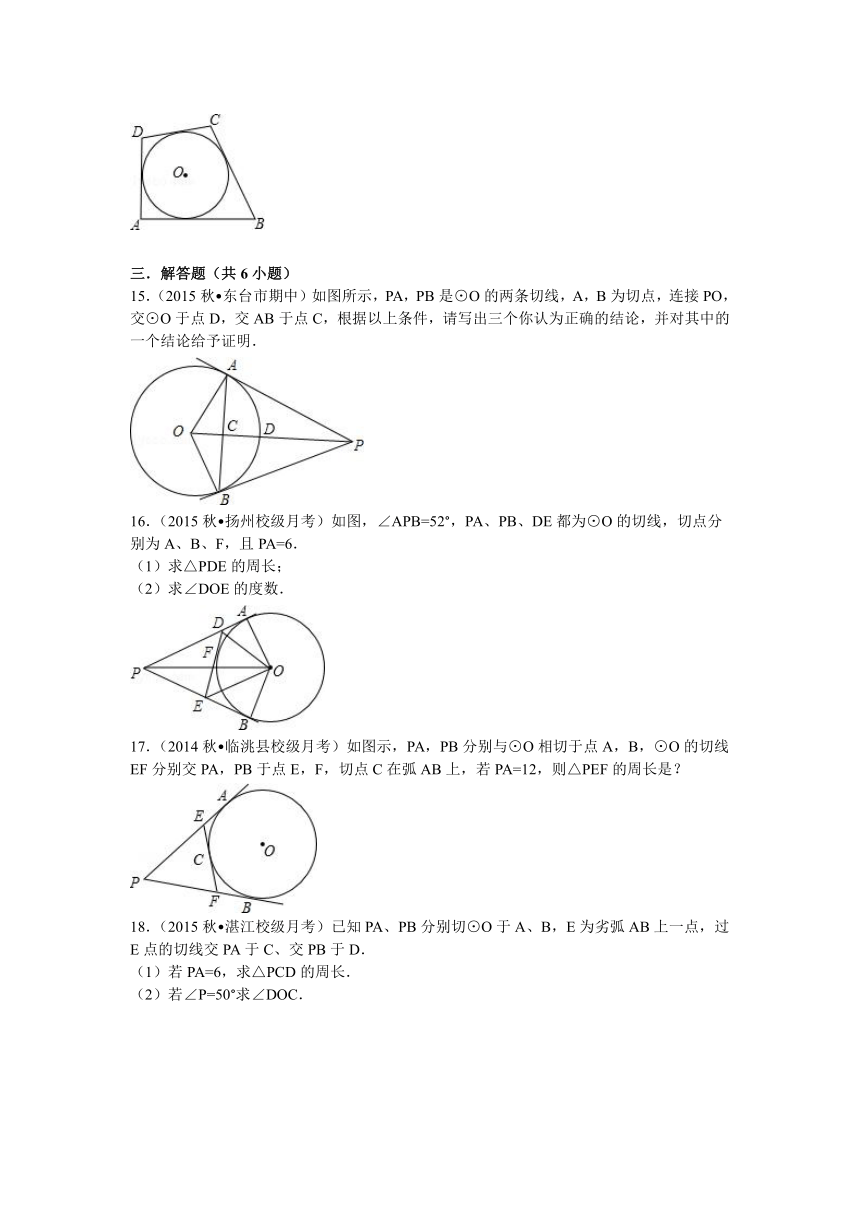
15.(2015秋 东台市期中)如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
16.(2015秋 扬州校级月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
17.(2014秋 临洮县校级月考)如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
18.(2015秋 湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
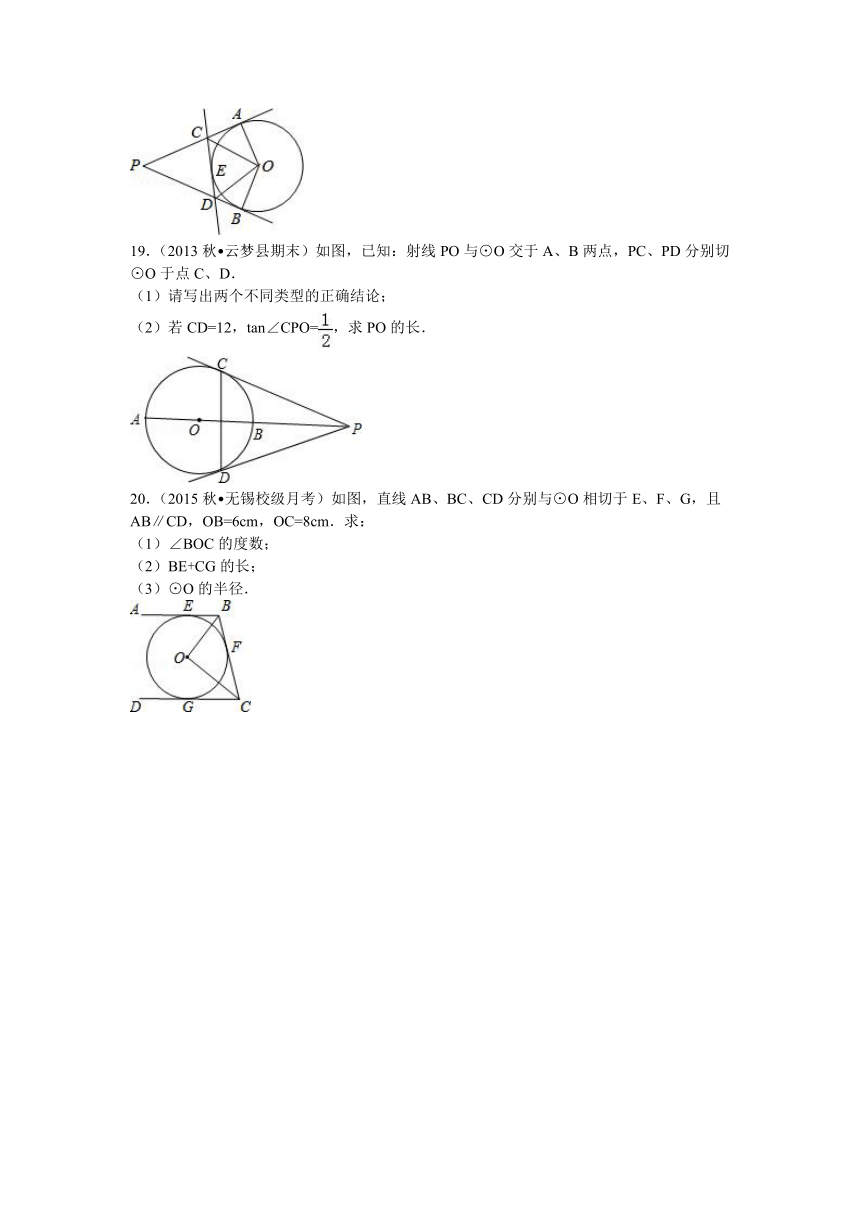
19.(2013秋 云梦县期末)如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=,求PO的长.
20.(2015秋 无锡校级月考)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 十堰二模)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2,则线段AB的长是( )
A.
B.3
C.2
D.3
【分析】直接利用切线长定理得出AC=EC,DE=DB,PA=PB,进而求出PA的长,然后判定三角形APB为等边三角形即可确定AB的长.
【解答】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB,
∵△PCD的周长等于3,
∴PA+PB=2,
∴PA=PB=,
链接PA和AO,
∵⊙O的半径为1,
∴sin∠APO===,
∴∠APO=30°,
∴∠APB=60°,
∴△APB是等边三角形,
∴AB=PA=PB=.
故选:A.
【点评】此题主要考查了切线长定理及解直角三角形的知识,熟练应用切线长定理是解题关键.
2.(2016 曲靖一模)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
A.5
B.7
C.8
D.10
【分析】根据切线长定理得到PB=PA、CA=CE,DE=DB,根据三角形的周长公式计算即可.
【解答】解:∵PA、PB分别切⊙O于点A、B,
∴PB=PA=4,
∵CD切⊙O于点E且分别交PA、PB于点C,D,
∴CA=CE,DE=DB,
∴△PCD的周长=PC+PD+CD=PC+CA+PD+DB=PA+PB=8,
故选:C.
【点评】本题考查的是切线长定理的应用,切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
3.(2015 东西湖区校级模拟)如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O
切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
A.9
B.10
C.3
D.2
【分析】作DH⊥BC于H,如图,利用平行线的性质得AB⊥AD,AB⊥BC,则根据切线的判定得到AD和BC为⊙O切线,根据切线长定理得DE=DA=2,CE=CB,NE=NF,MB=MF,利用四边形ABHD为矩形得BH=AD=2,DH=AB=6,设BC=x,则CH=x﹣2,CD=x+2,在Rt△DCH中根据勾股定理得(x﹣2)2+62=(x+2)2,解得x=,即CB=CE=,然后由等线段代换得到△MCN的周长=CE+CB=9.
【解答】解:作DH⊥BC于H,如图,
∵四边形ABCD中,AD平行BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC,
∵AB为直径,
∴AD和BC为⊙O
切线,
∵CD和MN为⊙O
切线,
∴DE=DA=2,CE=CB,NE=NF,MB=MF,
∵四边形ABHD为矩形,
∴BH=AD=2,DH=AB=6,
设BC=x,则CH=x﹣2,CD=x+2,
在Rt△DCH中,∵CH2+DH2=DC2,
∴(x﹣2)2+62=(x+2)2,解得x=,
∴CB=CE=,
∴△MCN的周长=CN+CM+MN
=CN+CM+NF+MF
=CN+CM+NF+MB
=CE+CB
=9.
故选A.
【点评】本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.也考查了勾股定理.
4.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( )
A.32
B.34
C.36
D.38
【分析】根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.
【解答】解:由题意可得圆外切四边形的两组对边和相等,
所以四边形的周长=2×(7+10)=34.
故选:B.
【点评】此题主要考查了切线长定理,熟悉圆外切四边形的性质:圆外切四边形的两组对边和相等是解题关键.
5.(2015 岳池县模拟)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是( )
A.
B.
C.
D.
【分析】利用切线长定理得出CA=CF,DF=DB,PA=PB,进而得出PA=r,求出即可.
【解答】解:∵PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,
∴CA=CF,DF=DB,PA=PB,
∴PC+CF+DF+PD=PA=PB=2PA=3r,
∴PA=r,
则的值是:=.
故选:D.
【点评】此题主要考查了切线长定理,得出PA的长是解题关键.
6.(2015秋 龙口市期末)如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm
B.7cm
C.6cm
D.随直线MN的变化而变化
【分析】利用切线长定理得出BC=BD+EC,DM=MF,FN=EN,AD=AE,进而得出答案.
【解答】解:设E、F分别是⊙O的切点,
∵△ABC是一张三角形的纸片,AB+BC+AC=17cm,⊙O是它的内切圆,点D是其中的一个切点,BC=5cm,
∴BD+CE=BC=5cm,则AD+AE=7cm,
故DM=MF,FN=EN,AD=AE,
∴AM+AN+MN=AD+AE=7(cm).
故选:B.
【点评】此题主要考查了切线长定理,得出AM+AN+MN=AD+AE是解题关键.
7.(2015秋 新北区校级月考)如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7
B.14
C.10.5
D.10
【分析】根据从圆外一点引圆的两条切线,它们的切线长相等和三角形的周长公式计算即可.
【解答】解:∵PA、PB、CD与⊙O相切于点为A、B、E,
∴PB=PA=7,CA=CE,DE=DB,
∴△PCD的周长=PC+CD+PB
=PC+CE+DE+PD
=PC+CA+DB+PD
=PA+PB=14,
故选:B.
【点评】本题考查的是切线长定理,从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
8.(2015秋 营口校级月考)已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.15cm
D.12.5cm
【分析】根据切线长定理得MA=MC,NC=NB,然后根据三角形周长的定义进行计算.
【解答】解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:C.
【点评】本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
9.(2014 齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
【分析】由于AE与圆O切于点F,根据切线长定理有AF=AB=4cm,EF=EC;设EF=EC=xcm.则DE=(4﹣x)cm,AE=(4+x)cm,
然后在三角形BCE中由勾股定理可以列出关于x的方程,解方程即可求出,然后就可以求出△ADE的面积.
【解答】解:∵AE与圆O切于点F,
显然根据切线长定理有AF=AB=4cm,EF=EC,
设EF=EC=xcm,
则DE=(4﹣x)cm,AE=(4+x)cm,
在三角形ADE中由勾股定理得:
(4﹣x)2+42=(4+x)2,
∴x=1cm,
∴CE=1cm,
∴DE=4﹣1=3cm,
∴S△ADE=AD DE÷2=3×4÷2=6cm2.
故选D.
【点评】此题主要考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出AB=AF,EF=EC.
10.(2014秋 德城区期末)如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm
B.15cm
C.10cm
D.随直线MN的变化而变化
【分析】利用切线长定理得出DM=MF,FN=EN,AD=AE,进而得出答案.
【解答】解:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,
∴设E、F分别是⊙O的切点,
故DM=MF,FN=EN,AD=AE,
∴AM+AN+MN=AD+AE=10+10=20(cm).
故选:A.
【点评】此题主要考查了切线长定理,得出AM+AN+MN=AD+AE是解题关键.
二.填空题(共4小题)
11.(2016 丹阳市校级模拟)如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于 1 .
【分析】根据切线的性质求得∠APO=30°,∠PAO=90°,再由直角三角形的性质得AO=1.
【解答】解:∵PA、PB是⊙O的两条切线,
∴∠APO=∠BPO=∠APB,∠PAO=90°
∵∠APB=60°,
∴∠APO=30°,
∵PO=2,
∴AO=1.
故答案为:1.
【点评】本题考查了切线长定理、切线的性质和直角三角形的性质,是基础知识要熟练掌握.
12.(2016春 合肥校级月考)如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是 12 .
【分析】由PA,PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理可得:PB=PA=6,CA=CE,DB=DE,继而可得△PCD的周长=PA+PB.
【解答】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=12.
故答案为:12.
【点评】此题考查了切线长定理.此题难度不大,注意从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
13.(2016春 盘锦校级月考)如图,圆外切四边形ABCD,且AB=15,CD=9,则四边形的周长是 48 .
【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
【解答】解:根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=2×(15+9)=48.
故答案为:48.
【点评】此题主要考查了切线长定理以及圆外切四边形的性质,正确利用圆外切四边形对边和相等是解题关键.
14.(2015 滨海县一模)如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为 52 .
【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
【解答】解:根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=52
故填:52
【点评】此题主要考查了圆外切四边形的性质,对边和相等.
三.解答题(共6小题)
15.(2015秋 东台市期中)如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
【分析】PA,PB是圆的切线得到∠OAP=∠OBP=90°,OA=OB,OP=OP,得到△OAP≌△OBP,∴AP=BP,∠7=∠8,又可得到△ACP≌△BCP和△AOC≌△BOC,∴∠3=∠4,∠5=∠6,由同角的余角相等得到∠1=∠5,∠2=∠6,△APB是等腰三角形,由顶角的平分线是底边上的高.得,OP⊥AB.
【解答】解:如图所示,结论:①∠3=∠4;或∠7=∠8;或∠1=∠5;或∠2=∠6;
②OP⊥AB;③AC=BC.
证明②:∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°.
在Rt△OAP与Rt△OBP中,
∵,
∴△OAP≌△OBP(HL),
∴PA=PB,∠3=∠4,
∴OP⊥AB.
【点评】本题是切线长定理的证明,利用切线的概念,全等三角形的判定和性质,等腰三角形的性质求解.
16.(2015秋 扬州校级月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
【分析】(1)根据切线长定理得到DA=DC,EB=EC,PA=PB=6,于是得到DE=DA+EB,即可得到结论;
(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOD=∠BOC,∠FOD=∠AOD=∠AOF,根据四边形的内角和得到∠AOB=360°﹣90°﹣90°﹣52°=128°,即可得到结论.
【解答】解:(1)∵PA、PB、DE都为⊙O的切线,
∴DA=DC,EB=EC,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12;
(2)连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOD=∠BOC,∠FOD=∠AOD=∠AOF,
∵∠APB=52°,
∴∠AOB=360°﹣90°﹣90°﹣52°=128°,
∴∠DOE=∠FOE+∠FOD=(∠BOF+∠AOF)=∠BOA=64°.
【点评】主要考查了切线的性质、切线长定理、勾股定理等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断.
17.(2014秋 临洮县校级月考)如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
【分析】由切线长定理知,AE=CE,FB=CF,PA=PB=12,然后根据△PEF的周长公式即可求出其结果
【解答】解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=12,
∴△PEF的周长=PE+EF+PF=PA+PB=24.
【点评】本题主要考查了切线长定理的应用,解此题的关键是求出△PEF的周长=PA+PB.
18.(2015秋 湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
【分析】(1)根据切线长定理得到PA=PB,AC=CE,BD=DE,根据三角形的周长公式计算即可;
(2)证明Rt△AOC≌Rt△EOC,得到∠AOC=∠COE和∠DOE=∠BOD,计算即可.
【解答】解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA
PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
【点评】本题考查的是切线长定理和全等三角形的判定和性质,掌握从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角是解题的关键.
19.(2013秋 云梦县期末)如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=,求PO的长.
【分析】(1)由切线长定理得①PC=PD,②∠CPO=∠DPA,由垂径定理得③CD⊥BA,④∠CEP=90°,由切割线定理得,⑤PC2=PA PB;
(2)连接OC,由切线长定理得PC=PD,∠CPO=∠DPA,再由垂径定理得DE,则求得CP,即可得OC,最后根据勾股定理得出OP的长.
【解答】解:(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DP,③ACD⊥BA,④∠CEP=90°,⑤PC2=PA PB;
(2)连接OC
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE=CD=6.
∵tan∠CPO=,
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO=,
∴
∴OC=3,
∴OP==15.
【点评】本题考查了切线长定理、勾股定理和垂径定理,是一道综合题,难度较大.
20.(2015秋 无锡校级月考)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
【分析】(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;
(2)由勾股定理可求得BC的长,进而由切线长定理即可得到BE+CG的长;
(3)最后由三角形面积公式即可求得OF的长.
【解答】解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°;
(2)由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴BE+CG=BC=10cm.
(3)∵OF⊥BC,
∴OF==4.8cm.
【点评】此题主要是综合运用了切线长定理和切线的性质定理.注意:求直角三角形斜边上的高时,可以借助直角三角形的面积进行计算.
一.选择题(共10小题)
1.(2016 十堰二模)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2,则线段AB的长是( )
A.
B.3
C.2
D.3
2.(2016 曲靖一模)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
A.5
B.7
C.8
D.10
3.(2015 东西湖区校级模拟)如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O
切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
A.9
B.10
C.3
D.2
4.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( )
A.32
B.34
C.36
D.38
5.(2015 岳池县模拟)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是( )
A.
B.
C.
D.
6.(2015秋 龙口市期末)如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm
B.7cm
C.6cm
D.随直线MN的变化而变化
7.(2015秋 新北区校级月考)如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7
B.14
C.10.5
D.10
8.(2015秋 营口校级月考)已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.15cm
D.12.5cm
9.(2014 齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
10.(2014秋 德城区期末)如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm
B.15cm
C.10cm
D.随直线MN的变化而变化
二.填空题(共4小题)
11.(2016 丹阳市校级模拟)如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于______.
12.(2016春 合肥校级月考)如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是______.
13.(2016春 盘锦校级月考)如图,圆外切四边形ABCD,且AB=15,CD=9,则四边形的周长是______.
14.(2015 滨海县一模)如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为______.
三.解答题(共6小题)
15.(2015秋 东台市期中)如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
16.(2015秋 扬州校级月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
17.(2014秋 临洮县校级月考)如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
18.(2015秋 湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
19.(2013秋 云梦县期末)如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=,求PO的长.
20.(2015秋 无锡校级月考)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 十堰二模)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2,则线段AB的长是( )
A.
B.3
C.2
D.3
【分析】直接利用切线长定理得出AC=EC,DE=DB,PA=PB,进而求出PA的长,然后判定三角形APB为等边三角形即可确定AB的长.
【解答】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB,
∵△PCD的周长等于3,
∴PA+PB=2,
∴PA=PB=,
链接PA和AO,
∵⊙O的半径为1,
∴sin∠APO===,
∴∠APO=30°,
∴∠APB=60°,
∴△APB是等边三角形,
∴AB=PA=PB=.
故选:A.
【点评】此题主要考查了切线长定理及解直角三角形的知识,熟练应用切线长定理是解题关键.
2.(2016 曲靖一模)如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
A.5
B.7
C.8
D.10
【分析】根据切线长定理得到PB=PA、CA=CE,DE=DB,根据三角形的周长公式计算即可.
【解答】解:∵PA、PB分别切⊙O于点A、B,
∴PB=PA=4,
∵CD切⊙O于点E且分别交PA、PB于点C,D,
∴CA=CE,DE=DB,
∴△PCD的周长=PC+PD+CD=PC+CA+PD+DB=PA+PB=8,
故选:C.
【点评】本题考查的是切线长定理的应用,切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
3.(2015 东西湖区校级模拟)如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O
切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
A.9
B.10
C.3
D.2
【分析】作DH⊥BC于H,如图,利用平行线的性质得AB⊥AD,AB⊥BC,则根据切线的判定得到AD和BC为⊙O切线,根据切线长定理得DE=DA=2,CE=CB,NE=NF,MB=MF,利用四边形ABHD为矩形得BH=AD=2,DH=AB=6,设BC=x,则CH=x﹣2,CD=x+2,在Rt△DCH中根据勾股定理得(x﹣2)2+62=(x+2)2,解得x=,即CB=CE=,然后由等线段代换得到△MCN的周长=CE+CB=9.
【解答】解:作DH⊥BC于H,如图,
∵四边形ABCD中,AD平行BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC,
∵AB为直径,
∴AD和BC为⊙O
切线,
∵CD和MN为⊙O
切线,
∴DE=DA=2,CE=CB,NE=NF,MB=MF,
∵四边形ABHD为矩形,
∴BH=AD=2,DH=AB=6,
设BC=x,则CH=x﹣2,CD=x+2,
在Rt△DCH中,∵CH2+DH2=DC2,
∴(x﹣2)2+62=(x+2)2,解得x=,
∴CB=CE=,
∴△MCN的周长=CN+CM+MN
=CN+CM+NF+MF
=CN+CM+NF+MB
=CE+CB
=9.
故选A.
【点评】本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.也考查了勾股定理.
4.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( )
A.32
B.34
C.36
D.38
【分析】根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.
【解答】解:由题意可得圆外切四边形的两组对边和相等,
所以四边形的周长=2×(7+10)=34.
故选:B.
【点评】此题主要考查了切线长定理,熟悉圆外切四边形的性质:圆外切四边形的两组对边和相等是解题关键.
5.(2015 岳池县模拟)如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是( )
A.
B.
C.
D.
【分析】利用切线长定理得出CA=CF,DF=DB,PA=PB,进而得出PA=r,求出即可.
【解答】解:∵PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,
∴CA=CF,DF=DB,PA=PB,
∴PC+CF+DF+PD=PA=PB=2PA=3r,
∴PA=r,
则的值是:=.
故选:D.
【点评】此题主要考查了切线长定理,得出PA的长是解题关键.
6.(2015秋 龙口市期末)如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm
B.7cm
C.6cm
D.随直线MN的变化而变化
【分析】利用切线长定理得出BC=BD+EC,DM=MF,FN=EN,AD=AE,进而得出答案.
【解答】解:设E、F分别是⊙O的切点,
∵△ABC是一张三角形的纸片,AB+BC+AC=17cm,⊙O是它的内切圆,点D是其中的一个切点,BC=5cm,
∴BD+CE=BC=5cm,则AD+AE=7cm,
故DM=MF,FN=EN,AD=AE,
∴AM+AN+MN=AD+AE=7(cm).
故选:B.
【点评】此题主要考查了切线长定理,得出AM+AN+MN=AD+AE是解题关键.
7.(2015秋 新北区校级月考)如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7
B.14
C.10.5
D.10
【分析】根据从圆外一点引圆的两条切线,它们的切线长相等和三角形的周长公式计算即可.
【解答】解:∵PA、PB、CD与⊙O相切于点为A、B、E,
∴PB=PA=7,CA=CE,DE=DB,
∴△PCD的周长=PC+CD+PB
=PC+CE+DE+PD
=PC+CA+DB+PD
=PA+PB=14,
故选:B.
【点评】本题考查的是切线长定理,从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
8.(2015秋 营口校级月考)已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.15cm
D.12.5cm
【分析】根据切线长定理得MA=MC,NC=NB,然后根据三角形周长的定义进行计算.
【解答】解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:C.
【点评】本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
9.(2014 齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
【分析】由于AE与圆O切于点F,根据切线长定理有AF=AB=4cm,EF=EC;设EF=EC=xcm.则DE=(4﹣x)cm,AE=(4+x)cm,
然后在三角形BCE中由勾股定理可以列出关于x的方程,解方程即可求出,然后就可以求出△ADE的面积.
【解答】解:∵AE与圆O切于点F,
显然根据切线长定理有AF=AB=4cm,EF=EC,
设EF=EC=xcm,
则DE=(4﹣x)cm,AE=(4+x)cm,
在三角形ADE中由勾股定理得:
(4﹣x)2+42=(4+x)2,
∴x=1cm,
∴CE=1cm,
∴DE=4﹣1=3cm,
∴S△ADE=AD DE÷2=3×4÷2=6cm2.
故选D.
【点评】此题主要考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出AB=AF,EF=EC.
10.(2014秋 德城区期末)如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm
B.15cm
C.10cm
D.随直线MN的变化而变化
【分析】利用切线长定理得出DM=MF,FN=EN,AD=AE,进而得出答案.
【解答】解:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,
∴设E、F分别是⊙O的切点,
故DM=MF,FN=EN,AD=AE,
∴AM+AN+MN=AD+AE=10+10=20(cm).
故选:A.
【点评】此题主要考查了切线长定理,得出AM+AN+MN=AD+AE是解题关键.
二.填空题(共4小题)
11.(2016 丹阳市校级模拟)如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于 1 .
【分析】根据切线的性质求得∠APO=30°,∠PAO=90°,再由直角三角形的性质得AO=1.
【解答】解:∵PA、PB是⊙O的两条切线,
∴∠APO=∠BPO=∠APB,∠PAO=90°
∵∠APB=60°,
∴∠APO=30°,
∵PO=2,
∴AO=1.
故答案为:1.
【点评】本题考查了切线长定理、切线的性质和直角三角形的性质,是基础知识要熟练掌握.
12.(2016春 合肥校级月考)如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是 12 .
【分析】由PA,PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理可得:PB=PA=6,CA=CE,DB=DE,继而可得△PCD的周长=PA+PB.
【解答】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=12.
故答案为:12.
【点评】此题考查了切线长定理.此题难度不大,注意从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
13.(2016春 盘锦校级月考)如图,圆外切四边形ABCD,且AB=15,CD=9,则四边形的周长是 48 .
【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
【解答】解:根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=2×(15+9)=48.
故答案为:48.
【点评】此题主要考查了切线长定理以及圆外切四边形的性质,正确利用圆外切四边形对边和相等是解题关键.
14.(2015 滨海县一模)如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为 52 .
【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
【解答】解:根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=52
故填:52
【点评】此题主要考查了圆外切四边形的性质,对边和相等.
三.解答题(共6小题)
15.(2015秋 东台市期中)如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
【分析】PA,PB是圆的切线得到∠OAP=∠OBP=90°,OA=OB,OP=OP,得到△OAP≌△OBP,∴AP=BP,∠7=∠8,又可得到△ACP≌△BCP和△AOC≌△BOC,∴∠3=∠4,∠5=∠6,由同角的余角相等得到∠1=∠5,∠2=∠6,△APB是等腰三角形,由顶角的平分线是底边上的高.得,OP⊥AB.
【解答】解:如图所示,结论:①∠3=∠4;或∠7=∠8;或∠1=∠5;或∠2=∠6;
②OP⊥AB;③AC=BC.
证明②:∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°.
在Rt△OAP与Rt△OBP中,
∵,
∴△OAP≌△OBP(HL),
∴PA=PB,∠3=∠4,
∴OP⊥AB.
【点评】本题是切线长定理的证明,利用切线的概念,全等三角形的判定和性质,等腰三角形的性质求解.
16.(2015秋 扬州校级月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
【分析】(1)根据切线长定理得到DA=DC,EB=EC,PA=PB=6,于是得到DE=DA+EB,即可得到结论;
(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOD=∠BOC,∠FOD=∠AOD=∠AOF,根据四边形的内角和得到∠AOB=360°﹣90°﹣90°﹣52°=128°,即可得到结论.
【解答】解:(1)∵PA、PB、DE都为⊙O的切线,
∴DA=DC,EB=EC,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12;
(2)连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOD=∠BOC,∠FOD=∠AOD=∠AOF,
∵∠APB=52°,
∴∠AOB=360°﹣90°﹣90°﹣52°=128°,
∴∠DOE=∠FOE+∠FOD=(∠BOF+∠AOF)=∠BOA=64°.
【点评】主要考查了切线的性质、切线长定理、勾股定理等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断.
17.(2014秋 临洮县校级月考)如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
【分析】由切线长定理知,AE=CE,FB=CF,PA=PB=12,然后根据△PEF的周长公式即可求出其结果
【解答】解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=12,
∴△PEF的周长=PE+EF+PF=PA+PB=24.
【点评】本题主要考查了切线长定理的应用,解此题的关键是求出△PEF的周长=PA+PB.
18.(2015秋 湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
【分析】(1)根据切线长定理得到PA=PB,AC=CE,BD=DE,根据三角形的周长公式计算即可;
(2)证明Rt△AOC≌Rt△EOC,得到∠AOC=∠COE和∠DOE=∠BOD,计算即可.
【解答】解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA
PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
【点评】本题考查的是切线长定理和全等三角形的判定和性质,掌握从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角是解题的关键.
19.(2013秋 云梦县期末)如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=,求PO的长.
【分析】(1)由切线长定理得①PC=PD,②∠CPO=∠DPA,由垂径定理得③CD⊥BA,④∠CEP=90°,由切割线定理得,⑤PC2=PA PB;
(2)连接OC,由切线长定理得PC=PD,∠CPO=∠DPA,再由垂径定理得DE,则求得CP,即可得OC,最后根据勾股定理得出OP的长.
【解答】解:(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DP,③ACD⊥BA,④∠CEP=90°,⑤PC2=PA PB;
(2)连接OC
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE=CD=6.
∵tan∠CPO=,
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO=,
∴
∴OC=3,
∴OP==15.
【点评】本题考查了切线长定理、勾股定理和垂径定理,是一道综合题,难度较大.
20.(2015秋 无锡校级月考)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
【分析】(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;
(2)由勾股定理可求得BC的长,进而由切线长定理即可得到BE+CG的长;
(3)最后由三角形面积公式即可求得OF的长.
【解答】解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°;
(2)由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴BE+CG=BC=10cm.
(3)∵OF⊥BC,
∴OF==4.8cm.
【点评】此题主要是综合运用了切线长定理和切线的性质定理.注意:求直角三角形斜边上的高时,可以借助直角三角形的面积进行计算.
