沪科版九年级数学下册25.2.2由三视图确定几何体及计算测试卷(解析版)
文档属性
| 名称 | 沪科版九年级数学下册25.2.2由三视图确定几何体及计算测试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 00:00:00 | ||
图片预览

文档简介
沪科版九年级数学下册25.2.2《由三视图确定几何体及计算》
测
试
卷
一.选择题(共10小题)
1.(2016 天门)下面几个几何体,主视图是圆的是( )
A.
B.
C.
D.
2.(2016 鄂州)一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是( )
A.
B.
C.
D.
3.(2016 金华)从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
A.
B.
C.
D.
4.(2016 杭州)下列选项中,如图所示的圆柱的三视图画法正确的是( )
A.
B.
C.
D.
5.(2016 朝阳)如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
A.
B.
C.
D.
6.(2016 衢州)如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
A.
B.
C.
D.
7.(2016 温州)三本相同的书本叠成如图所示的几何体,它的主视图是( )
A.
B.
C.
D.
8.(2016 常州)如图所示是一个几何体的三视图,这个几何体的名称是( )
A.圆柱体
B.三棱锥
C.球体
D.圆锥体
9.(2016 贺州)一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥
B.三棱柱
C.圆柱
D.长方体
10.(2016 随州)如图是某工件的三视图,则此工件的表面积为( )
A.15πcm2
B.51πcm2
C.66πcm2
D.24πcm2
二.填空题(共4小题)
11.(2016春 潮南区月考)一个圆柱的俯视图是______,左视图是______.
12.(2016春 利川市校级月考)将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的______(只填序号).
13.(2016 盐城)如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为______.
14.(2016 荆州)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为______cm2.
三.解答题(共6小题)
15.(2012秋 建平县期中)如图,水平放置的长方体的底面是边长为2cm和4cm的矩形,它的左视图的面积为6cm2,则长方体的体积是多少?
16.(2008秋 安宁市校级期末)请你画出如图几何体的三视图.
17.(2015秋 历城区期中)学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
18.(2013秋 昆山市期末)如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
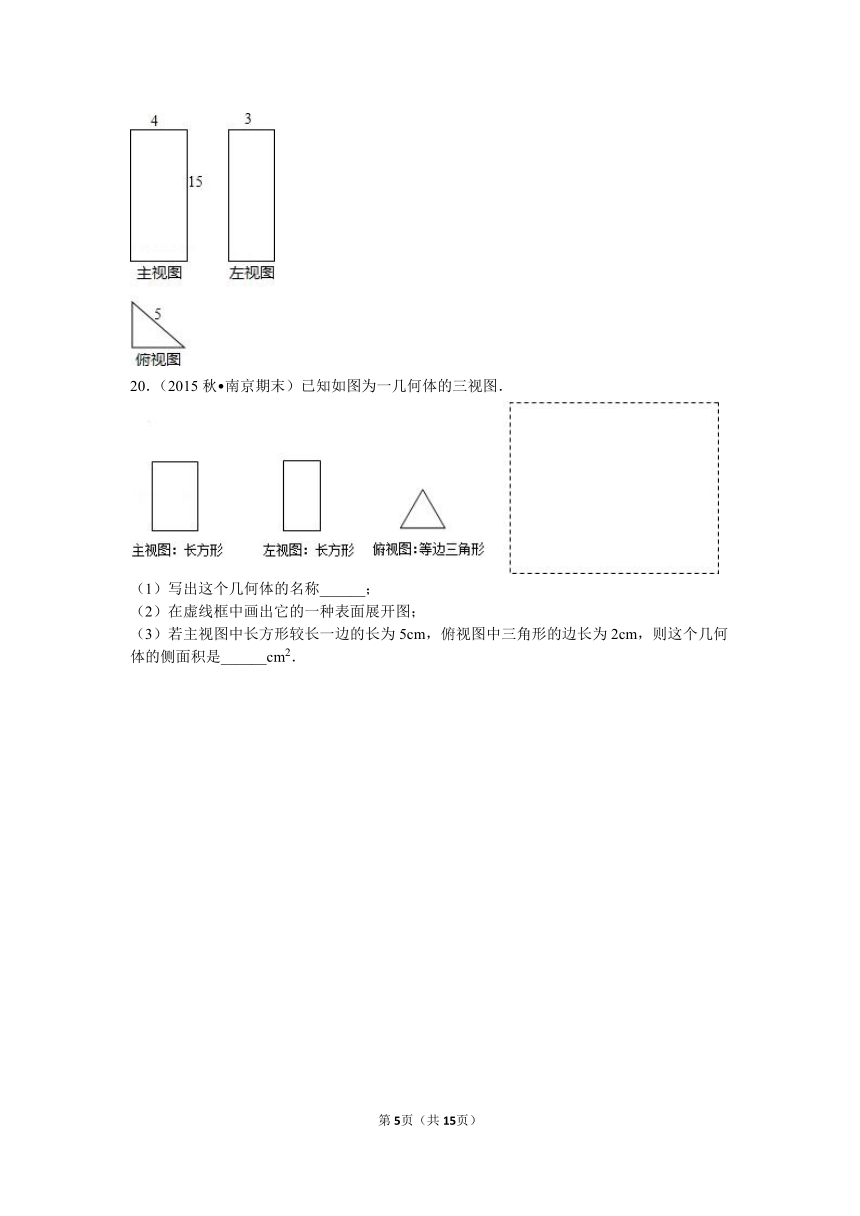
19.(2016春 潮南区月考)如图所示的是某个几何体的三视图.
(1)说出这个立体图形的名称;
(2)根据图中的有关数据,求这个几何体的表面积.
20.(2015秋 南京期末)已知如图为一几何体的三视图.
(1)写出这个几何体的名称______;
(2)在虚线框中画出它的一种表面展开图;
(3)若主视图中长方形较长一边的长为5cm,俯视图中三角形的边长为2cm,则这个几何体的侧面积是______cm2.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 天门)下面几个几何体,主视图是圆的是( )
A.
B.
C.
D.
【分析】分别判断A,B,C,D的主视图,即可解答.
【解答】解:A、主视图为正方形,故错误;
B、主视图为圆,正确;
C、主视图为三角形,故错误;
D、主视图为长方形,故错误;
故选:B.
【点评】本题考查了几何体的三视图,解决本题的关键是得出各个几何体的主视图.
2.(2016 鄂州)一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是( )
A.
B.
C.
D.
【分析】从左面看会看到该几何体的两个侧面.
【解答】解:从左边看去,应该是两个并列并且大小相同的矩形,故选B.
【点评】本题考查了几何体的三视图及空间想象能力.
3.(2016 金华)从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
A.
B.
C.
D.
【分析】直接利用左视图的观察角度,进而得出视图.
【解答】解:如图所示:∵从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,
∴该几何体的左视图为:.
故选:C.
【点评】此题主要考查了简单几何体的三视图,正确把握观察角度是解题关键.
4.(2016 杭州)下列选项中,如图所示的圆柱的三视图画法正确的是( )
A.
B.
C.
D.
【分析】根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,可得答案.
【解答】解:该圆柱体的主视图、俯视图均为矩形,左视图为圆,
故选:A.
【点评】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
5.(2016 朝阳)如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
A.
B.
C.
D.
【分析】从正面看几何体得到主视图即可.
【解答】解:根据题意的主视图为:,
故选B
【点评】此题考查了简单组合体的三视图,主视图是从物体的正面看得到的视图.
6.(2016 衢州)如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
A.
B.
C.
D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看,圆锥看见的是:圆和点,两个正方体看见的是两个正方形.
故答案为:C.
【点评】此题主要考查了三视图的知识,关键是掌握三视图的几种看法.
7.(2016 温州)三本相同的书本叠成如图所示的几何体,它的主视图是( )
A.
B.
C.
D.
【分析】主视图是分别从物体正面看,所得到的图形.
【解答】解:观察图形可知,三本相同的书本叠成如图所示的几何体,它的主视图是.
故选:B.
【点评】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
8.(2016 常州)如图所示是一个几何体的三视图,这个几何体的名称是( )
A.圆柱体
B.三棱锥
C.球体
D.圆锥体
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:由于主视图和左视图为长方形可得此几何体为柱体,
由俯视图为圆可得为圆柱体.
故选A.
【点评】本题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力.
9.(2016 贺州)一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥
B.三棱柱
C.圆柱
D.长方体
【分析】根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱
【解答】解:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选:B.
【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.
10.(2016 随州)如图是某工件的三视图,则此工件的表面积为( )
A.15πcm2
B.51πcm2
C.66πcm2
D.24πcm2
【分析】根据三视图,可得几何体是圆锥,根据勾股定理,可得圆锥的母线长,根据扇形的面积公式,可得圆锥的侧面积,根据圆的面积公式,可得圆锥的底面积,可得答案.
【解答】解:由三视图,得:
OB=3cm,0A=4cm,
由勾股定理,得AB==5cm,
圆锥的侧面积×6π×5=15π(cm2),
圆锥的底面积π×()2=9π(cm2),
圆锥的表面积15π+9π=24π(cm2),
故选:D.
【点评】本题考查了由三视图判断几何体,利用三视图得出圆锥是解题关键,注意圆锥的侧面积等于圆锥的底面周长与母线长乘积的一半.
二.填空题(共4小题)
11.(2016春 潮南区月考)一个圆柱的俯视图是 圆 ,左视图是 矩形 .
【分析】一个物体从上往下看得到的图叫做俯视图,从左往右看得到的图叫做左视图,据此求解即可.
【解答】解:一个圆柱的俯视图是圆,左视图是矩形.
故答案为圆,矩形.
【点评】本题考查了几何体的三视图的判断,属于基础知识,比较简单.
12.(2016春 利川市校级月考)将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的 ③ (只填序号).
【分析】易得此几何体为两个底面相同且相连的圆锥的组合体,主视图是从几何体正面看到的图形.
【解答】解:Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等相连的圆锥,圆锥的主视图是等腰三角形,所以该几何体的左视图是两个底边相等的等腰三角形相连,并且上面的等腰三角形较大,故为图③.
故答案为:③.
【点评】本题考查了空间想象能力及几何体的三视图;发挥空间想象能力,确定旋转一周所得的几何体形状是关键.
13.(2016 盐城)如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为 5 .
【分析】根据立体图形画出它的主视图,再求出面积.
【解答】解:主视图如图所示,
∵由6个棱长均为1的正方体组成的几何体,
∴主视图的面积为5×12=5,
故答案为5.
【点评】此题是简单组合体的三视图,主要考查了立体图的主视图,解本题的关键是画出它的主视图.
14.(2016 荆州)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为 4π cm2.
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状,确定圆锥的母线长和底面半径,从而确定其表面积.
【解答】解:由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
根据三视图知:该圆锥的母线长为3cm,底面半径为1cm,
故表面积=πrl+πr2=π×1×3+π×12=4πcm2.
故答案为:4π.
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
三.解答题(共6小题)
15.(2012秋 建平县期中)如图,水平放置的长方体的底面是边长为2cm和4cm的矩形,它的左视图的面积为6cm2,则长方体的体积是多少?
【分析】根据长方体的体积公式可得:6×4=24cm3.
【解答】解:根据题意,得:6×4=24(cm3),
因此,长方体的体积是24cm3.
【点评】此题主要考查了简单几何体的三视图,关键是掌握长方体的体积公式.
16.(2008秋 安宁市校级期末)请你画出如图几何体的三视图.
【分析】从正面,左面,上面看圆柱得到的图形分别是长方形,长方形,圆.
【解答】解:如图所示:
【点评】此题主要考查了简单几何体的三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.
17.(2015秋 历城区期中)学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
【分析】由表中给出的碟子个数与碟子高度的规律,可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1).
【解答】解:由题意得:
(1)2+1.5(x﹣1)=1.5x+0.5
(2)由三视图可知共有12个碟子
∴叠成一摞的高度=1.5×12+0.5=18.5(cm)
【点评】考查获取信息(读表)、分析问题解决问题的能力.
找出碟子个数与碟子高度的之间的关系式是此题的关键.
18.(2013秋 昆山市期末)如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体体积+上面圆柱的体积即可求解.
【解答】解:(1)如图所示:
;
(2)2×5×8+π×(2÷2)2×6
=80+π×1×6
=80+6π.
答:这个组合几何体的体积是80+6π.
【点评】此题主要考查了简单几何体的三视图,以及几何体的表面积,关键是掌握三视图所看的位置.
19.(2016春 潮南区月考)如图所示的是某个几何体的三视图.
(1)说出这个立体图形的名称;
(2)根据图中的有关数据,求这个几何体的表面积.
【分析】(1)从三视图的主视图看这是一个矩形,而左视图是一个扁平的矩形,俯视图为一个三角形,故可知道这是一个直三棱柱;
(2)根据直三棱柱的表面积公式计算即可.
【解答】解:(1)这个立体图形是直三棱柱;
(2)表面积为:×3×4×2+15×3+15×4+15×5=192.
【点评】本题主要考查由三视图确定几何体和求几何体的表面积等相关知识,考查学生的空间想象能力.
20.(2015秋 南京期末)已知如图为一几何体的三视图.
(1)写出这个几何体的名称 正三棱柱 ;
(2)在虚线框中画出它的一种表面展开图;
(3)若主视图中长方形较长一边的长为5cm,俯视图中三角形的边长为2cm,则这个几何体的侧面积是 30 cm2.
【分析】(1)只有棱柱的主视图和左视图才能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;
(2)应该会出现三个长方形,两个三角形;
(3)侧面积为3个长方形,每一个长方形的长和宽分别为5cm,2cm,计算出一个长方形的面积,乘3即可.
【解答】解:(1)这个几何体是正三棱柱;
(2)表面展开图如下:
;
(3)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长即
C=3×2=6cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为:
S=6×5=30cm2.
答:这个几何体的侧面面积为30cm2.
故答案为正三棱柱;
【点评】此题考查由三视图判断几何体,掌握棱柱的侧面都是长方形,上下底面是几边形就是几棱柱是解决问题的关键.
第1页(共1页)
测
试
卷
一.选择题(共10小题)
1.(2016 天门)下面几个几何体,主视图是圆的是( )
A.
B.
C.
D.
2.(2016 鄂州)一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是( )
A.
B.
C.
D.
3.(2016 金华)从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
A.
B.
C.
D.
4.(2016 杭州)下列选项中,如图所示的圆柱的三视图画法正确的是( )
A.
B.
C.
D.
5.(2016 朝阳)如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
A.
B.
C.
D.
6.(2016 衢州)如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
A.
B.
C.
D.
7.(2016 温州)三本相同的书本叠成如图所示的几何体,它的主视图是( )
A.
B.
C.
D.
8.(2016 常州)如图所示是一个几何体的三视图,这个几何体的名称是( )
A.圆柱体
B.三棱锥
C.球体
D.圆锥体
9.(2016 贺州)一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥
B.三棱柱
C.圆柱
D.长方体
10.(2016 随州)如图是某工件的三视图,则此工件的表面积为( )
A.15πcm2
B.51πcm2
C.66πcm2
D.24πcm2
二.填空题(共4小题)
11.(2016春 潮南区月考)一个圆柱的俯视图是______,左视图是______.
12.(2016春 利川市校级月考)将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的______(只填序号).
13.(2016 盐城)如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为______.
14.(2016 荆州)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为______cm2.
三.解答题(共6小题)
15.(2012秋 建平县期中)如图,水平放置的长方体的底面是边长为2cm和4cm的矩形,它的左视图的面积为6cm2,则长方体的体积是多少?
16.(2008秋 安宁市校级期末)请你画出如图几何体的三视图.
17.(2015秋 历城区期中)学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
18.(2013秋 昆山市期末)如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
19.(2016春 潮南区月考)如图所示的是某个几何体的三视图.
(1)说出这个立体图形的名称;
(2)根据图中的有关数据,求这个几何体的表面积.
20.(2015秋 南京期末)已知如图为一几何体的三视图.
(1)写出这个几何体的名称______;
(2)在虚线框中画出它的一种表面展开图;
(3)若主视图中长方形较长一边的长为5cm,俯视图中三角形的边长为2cm,则这个几何体的侧面积是______cm2.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 天门)下面几个几何体,主视图是圆的是( )
A.
B.
C.
D.
【分析】分别判断A,B,C,D的主视图,即可解答.
【解答】解:A、主视图为正方形,故错误;
B、主视图为圆,正确;
C、主视图为三角形,故错误;
D、主视图为长方形,故错误;
故选:B.
【点评】本题考查了几何体的三视图,解决本题的关键是得出各个几何体的主视图.
2.(2016 鄂州)一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是( )
A.
B.
C.
D.
【分析】从左面看会看到该几何体的两个侧面.
【解答】解:从左边看去,应该是两个并列并且大小相同的矩形,故选B.
【点评】本题考查了几何体的三视图及空间想象能力.
3.(2016 金华)从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
A.
B.
C.
D.
【分析】直接利用左视图的观察角度,进而得出视图.
【解答】解:如图所示:∵从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,
∴该几何体的左视图为:.
故选:C.
【点评】此题主要考查了简单几何体的三视图,正确把握观察角度是解题关键.
4.(2016 杭州)下列选项中,如图所示的圆柱的三视图画法正确的是( )
A.
B.
C.
D.
【分析】根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,可得答案.
【解答】解:该圆柱体的主视图、俯视图均为矩形,左视图为圆,
故选:A.
【点评】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
5.(2016 朝阳)如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
A.
B.
C.
D.
【分析】从正面看几何体得到主视图即可.
【解答】解:根据题意的主视图为:,
故选B
【点评】此题考查了简单组合体的三视图,主视图是从物体的正面看得到的视图.
6.(2016 衢州)如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
A.
B.
C.
D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看,圆锥看见的是:圆和点,两个正方体看见的是两个正方形.
故答案为:C.
【点评】此题主要考查了三视图的知识,关键是掌握三视图的几种看法.
7.(2016 温州)三本相同的书本叠成如图所示的几何体,它的主视图是( )
A.
B.
C.
D.
【分析】主视图是分别从物体正面看,所得到的图形.
【解答】解:观察图形可知,三本相同的书本叠成如图所示的几何体,它的主视图是.
故选:B.
【点评】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
8.(2016 常州)如图所示是一个几何体的三视图,这个几何体的名称是( )
A.圆柱体
B.三棱锥
C.球体
D.圆锥体
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:由于主视图和左视图为长方形可得此几何体为柱体,
由俯视图为圆可得为圆柱体.
故选A.
【点评】本题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力.
9.(2016 贺州)一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥
B.三棱柱
C.圆柱
D.长方体
【分析】根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱
【解答】解:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选:B.
【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.
10.(2016 随州)如图是某工件的三视图,则此工件的表面积为( )
A.15πcm2
B.51πcm2
C.66πcm2
D.24πcm2
【分析】根据三视图,可得几何体是圆锥,根据勾股定理,可得圆锥的母线长,根据扇形的面积公式,可得圆锥的侧面积,根据圆的面积公式,可得圆锥的底面积,可得答案.
【解答】解:由三视图,得:
OB=3cm,0A=4cm,
由勾股定理,得AB==5cm,
圆锥的侧面积×6π×5=15π(cm2),
圆锥的底面积π×()2=9π(cm2),
圆锥的表面积15π+9π=24π(cm2),
故选:D.
【点评】本题考查了由三视图判断几何体,利用三视图得出圆锥是解题关键,注意圆锥的侧面积等于圆锥的底面周长与母线长乘积的一半.
二.填空题(共4小题)
11.(2016春 潮南区月考)一个圆柱的俯视图是 圆 ,左视图是 矩形 .
【分析】一个物体从上往下看得到的图叫做俯视图,从左往右看得到的图叫做左视图,据此求解即可.
【解答】解:一个圆柱的俯视图是圆,左视图是矩形.
故答案为圆,矩形.
【点评】本题考查了几何体的三视图的判断,属于基础知识,比较简单.
12.(2016春 利川市校级月考)将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的 ③ (只填序号).
【分析】易得此几何体为两个底面相同且相连的圆锥的组合体,主视图是从几何体正面看到的图形.
【解答】解:Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等相连的圆锥,圆锥的主视图是等腰三角形,所以该几何体的左视图是两个底边相等的等腰三角形相连,并且上面的等腰三角形较大,故为图③.
故答案为:③.
【点评】本题考查了空间想象能力及几何体的三视图;发挥空间想象能力,确定旋转一周所得的几何体形状是关键.
13.(2016 盐城)如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为 5 .
【分析】根据立体图形画出它的主视图,再求出面积.
【解答】解:主视图如图所示,
∵由6个棱长均为1的正方体组成的几何体,
∴主视图的面积为5×12=5,
故答案为5.
【点评】此题是简单组合体的三视图,主要考查了立体图的主视图,解本题的关键是画出它的主视图.
14.(2016 荆州)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为 4π cm2.
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状,确定圆锥的母线长和底面半径,从而确定其表面积.
【解答】解:由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
根据三视图知:该圆锥的母线长为3cm,底面半径为1cm,
故表面积=πrl+πr2=π×1×3+π×12=4πcm2.
故答案为:4π.
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
三.解答题(共6小题)
15.(2012秋 建平县期中)如图,水平放置的长方体的底面是边长为2cm和4cm的矩形,它的左视图的面积为6cm2,则长方体的体积是多少?
【分析】根据长方体的体积公式可得:6×4=24cm3.
【解答】解:根据题意,得:6×4=24(cm3),
因此,长方体的体积是24cm3.
【点评】此题主要考查了简单几何体的三视图,关键是掌握长方体的体积公式.
16.(2008秋 安宁市校级期末)请你画出如图几何体的三视图.
【分析】从正面,左面,上面看圆柱得到的图形分别是长方形,长方形,圆.
【解答】解:如图所示:
【点评】此题主要考查了简单几何体的三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.
17.(2015秋 历城区期中)学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
【分析】由表中给出的碟子个数与碟子高度的规律,可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1).
【解答】解:由题意得:
(1)2+1.5(x﹣1)=1.5x+0.5
(2)由三视图可知共有12个碟子
∴叠成一摞的高度=1.5×12+0.5=18.5(cm)
【点评】考查获取信息(读表)、分析问题解决问题的能力.
找出碟子个数与碟子高度的之间的关系式是此题的关键.
18.(2013秋 昆山市期末)如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体体积+上面圆柱的体积即可求解.
【解答】解:(1)如图所示:
;
(2)2×5×8+π×(2÷2)2×6
=80+π×1×6
=80+6π.
答:这个组合几何体的体积是80+6π.
【点评】此题主要考查了简单几何体的三视图,以及几何体的表面积,关键是掌握三视图所看的位置.
19.(2016春 潮南区月考)如图所示的是某个几何体的三视图.
(1)说出这个立体图形的名称;
(2)根据图中的有关数据,求这个几何体的表面积.
【分析】(1)从三视图的主视图看这是一个矩形,而左视图是一个扁平的矩形,俯视图为一个三角形,故可知道这是一个直三棱柱;
(2)根据直三棱柱的表面积公式计算即可.
【解答】解:(1)这个立体图形是直三棱柱;
(2)表面积为:×3×4×2+15×3+15×4+15×5=192.
【点评】本题主要考查由三视图确定几何体和求几何体的表面积等相关知识,考查学生的空间想象能力.
20.(2015秋 南京期末)已知如图为一几何体的三视图.
(1)写出这个几何体的名称 正三棱柱 ;
(2)在虚线框中画出它的一种表面展开图;
(3)若主视图中长方形较长一边的长为5cm,俯视图中三角形的边长为2cm,则这个几何体的侧面积是 30 cm2.
【分析】(1)只有棱柱的主视图和左视图才能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;
(2)应该会出现三个长方形,两个三角形;
(3)侧面积为3个长方形,每一个长方形的长和宽分别为5cm,2cm,计算出一个长方形的面积,乘3即可.
【解答】解:(1)这个几何体是正三棱柱;
(2)表面展开图如下:
;
(3)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长即
C=3×2=6cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为:
S=6×5=30cm2.
答:这个几何体的侧面面积为30cm2.
故答案为正三棱柱;
【点评】此题考查由三视图判断几何体,掌握棱柱的侧面都是长方形,上下底面是几边形就是几棱柱是解决问题的关键.
第1页(共1页)
