沪科版九年级数学下册24.6.2正多边形的性质测试卷(解析版)
文档属性
| 名称 | 沪科版九年级数学下册24.6.2正多边形的性质测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 00:00:00 | ||
图片预览



文档简介
沪科版九年级数学下册24.6.2《正多边形的性质》测试卷
一.选择题(共10小题)
1.(2016 曲靖)如图,AD,BE,CF是正六边形ABCDEF的对角线,图中平行四边形的个数有( )
A.2个
B.4个
C.6个
D.8个
2.(2016 泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.
B.
C.
D.
3.(2016 南京)已知正六边形的边长为2,则它的内切圆的半径为( )
A.1
B.
C.2
D.2
4.(2016 南平)若正六边形的半径长为4,则它的边长等于( )
A.4
B.2
C.2
D.4
5.(2016 东平县二模)已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
6.(2016 湘潭一模)已知正三角形外接圆半径为2,这个正三角形的边长是( )
A.2
B.
C.3
D.2
7.(2016 南开区一模)正六边形的边心距与边长之比为( )
A.1:2
B.:2
C.:1
D.:2
8.(2016 宜昌模拟)正三角形内切圆与外接圆半径之比为( )
A.
B.
C.
D.
9.(2016 普陀区二模)如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
A.2cm
B.2cm
C.4cm
D.4Cm
10.(2016 开平区一模)如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.
B.2
C.
D.3
二.填空题(共4小题)
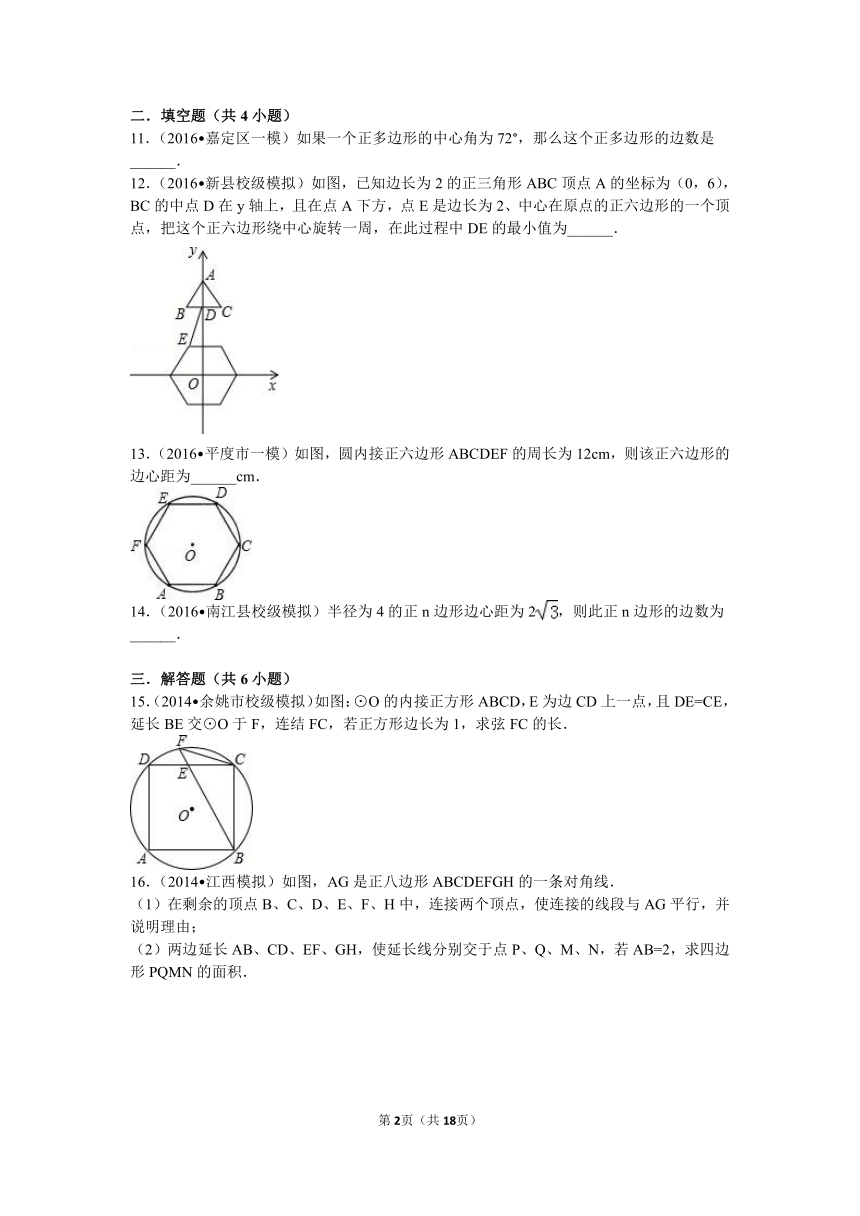
11.(2016 嘉定区一模)如果一个正多边形的中心角为72°,那么这个正多边形的边数是______.
12.(2016 新县校级模拟)如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为______.
13.(2016 平度市一模)如图,圆内接正六边形ABCDEF的周长为12cm,则该正六边形的边心距为______cm.
14.(2016 南江县校级模拟)半径为4的正n边形边心距为2,则此正n边形的边数为______.
三.解答题(共6小题)
15.(2014 余姚市校级模拟)如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
16.(2014 江西模拟)如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
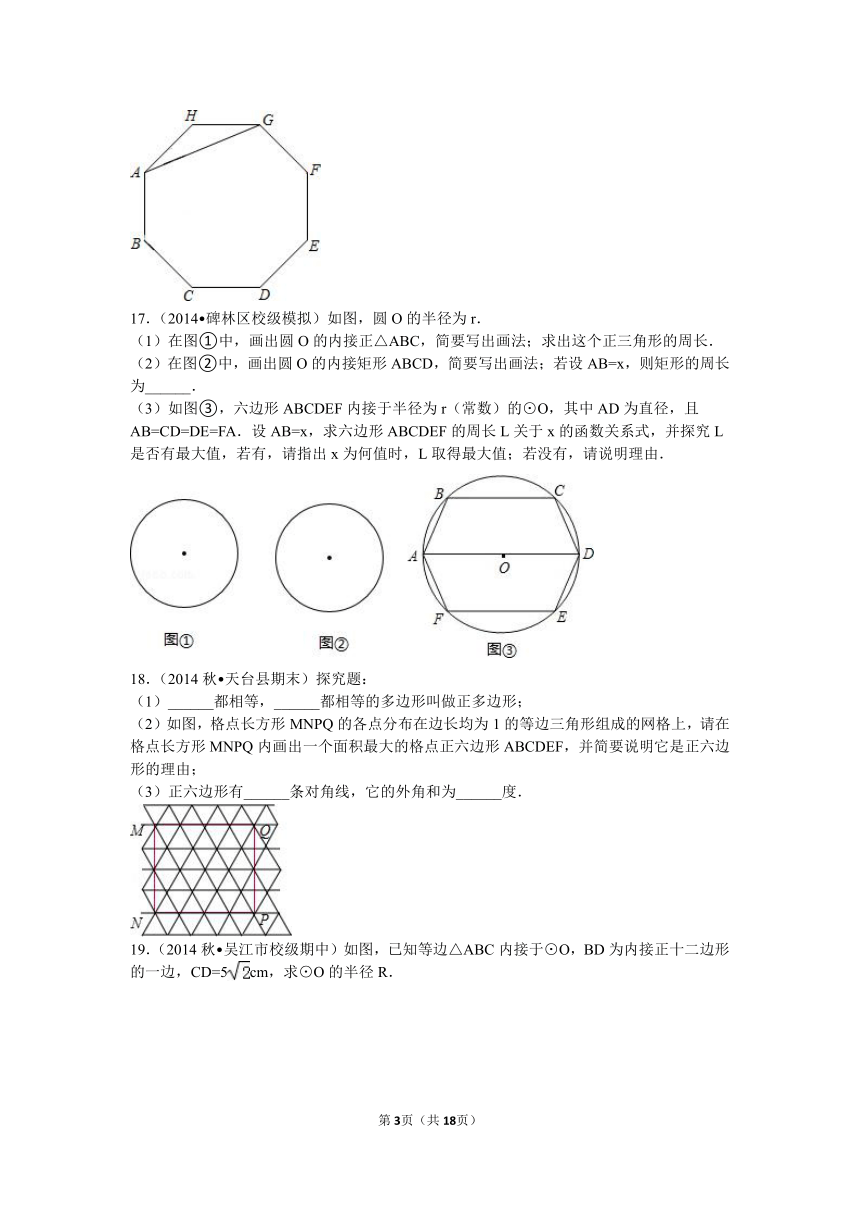
17.(2014 碑林区校级模拟)如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为______.
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
18.(2014秋 天台县期末)探究题:
(1)______都相等,______都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上,请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有______条对角线,它的外角和为______度.
19.(2014秋 吴江市校级期中)如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
20.(2014秋 渠县校级期中)如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
①求这个正六边形的边长.
②求这个正六边形的边心距.
③设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 曲靖)如图,AD,BE,CF是正六边形ABCDEF的对角线,图中平行四边形的个数有( )
A.2个
B.4个
C.6个
D.8个
【分析】根据正六边形的性质,直接判断即可;
【解答】解:如图,
∵AD,BE,CF是正六边形ABCDEF的对角线,
∴OA=OE=AF=EF,
∴四边形AOEF是平行四边形,
同理:四边形DEFO,四边形ABCO,四边形BCDO,四边形CDEO,四边形FABOD都是平行四边形,共6个,
故选C
【点评】此题是正多边形和圆,主要考查了正六边形的性质,平行四边形的判定,掌握平行四边形的判定是解本题的关键.注意:数平行四边形个数时,按顺时针或逆时针数.
2.(2016 泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.
B.
C.
D.
【分析】由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
【解答】解:如图1,
∵OC=1,
∴OD=1×sin30°=;
如图2,
∵OB=1,
∴OE=1×sin45°=;
如图3,
∵OA=1,
∴OD=1×cos30°=,
则该三角形的三边分别为:、、,
∵()2+()2=()2,
∴该三角形是以、为直角边,为斜边的直角三角形,
∴该三角形的面积是××=,
故选:D.
【点评】本题主要考查多边形与圆,解答此题要明确:多边形的半径、边心距、中心角等概念,根据解直角三角形的知识解答是解题的关键.
3.(2016 南京)已知正六边形的边长为2,则它的内切圆的半径为( )
A.1
B.
C.2
D.2
【分析】根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
【解答】解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA sin60°=2×=,
∴边长为2的正六边形的内切圆的半径为.
故选B.
【点评】本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算,记住基本概念是解题的关键,属于中考常考题型.
4.(2016 南平)若正六边形的半径长为4,则它的边长等于( )
A.4
B.2
C.2
D.4
【分析】根据正六边形的外接圆半径和正六边形的边长将组成一个等边三角形,即可求解.
【解答】解:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,
故正六边形的半径等于4,则正六边形的边长是4.
故选:A.
【点评】此题主要考查了正多边形和圆,利用正六边形的外接圆半径和正六边形的边长将组成一个等边三角形得出是解题关键.
5.(2016 东平县二模)已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
【分析】过中心作边的垂线,连接半径,把内切圆半径,外接圆半径和高,中心角之间的计转化为解直角三角形.
【解答】解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选D.
【点评】正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径,外接圆半径和高,中心角之间的计转化为解直角三角形.
6.(2016 湘潭一模)已知正三角形外接圆半径为2,这个正三角形的边长是( )
A.2
B.
C.3
D.2
【分析】易得正三角形的中心角为120°,那么中心角的一半为60°,利用60°的正弦值可得正三角形边长的一半,乘以2即为正三角形的边长.
【解答】解:如图OA=2,求AB长.
∠AOB=360°÷3=120°
连接OA,OB,作OC⊥AB于点C,
∵OA=OB,
∴AB=2AC,∠AOC=60°,
∴AC=OA×sin60°=cm,
∴AB=2AC=2cm,
故选A.
【点评】考查有关正多边形和圆的相关计算;利用垂径定理和相应的三角函数知识得到AC的值是解决本题
的关键.
7.(2016 南开区一模)正六边形的边心距与边长之比为( )
A.1:2
B.:2
C.:1
D.:2
【分析】首先根据题意画出图形,然后设六边形的边长是a,由勾股定理即可求得OC的长,继而求得答案.
【解答】解:如图:设正六边形的边长是a,则半径长也是a;
经过正六边形的中心O作边AB的垂线段OC,则AC=AB=a,
于是OC==a,
所以正六边形的边心距与边长之比为:a:a=:2.
故选:D.
【点评】此题考查了正多边形和圆的关系.此题难度不大,注意掌握数形结合思想的应用.
8.(2016 宜昌模拟)正三角形内切圆与外接圆半径之比为( )
A.
B.
C.
D.
【分析】先作出图形,根据等边三角形的性质确定它的内切圆和外接圆的圆心;通过特殊角进行计算,用内切圆半径来表示外接圆半径,最后求出比值即可.
【解答】解:如图,△ABC是等边三角形,AD是高.点O是其外接圆的圆心,由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BO=2OD,而OA=OB,
∴OD:OA=1:2.
故选A.
【点评】本题考查的是正多边形和圆,熟知等边三角形的性质及三角形内切圆与外接圆的定义是解答此题的关键.
9.(2016 普陀区二模)如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
A.2cm
B.2cm
C.4cm
D.4Cm
【分析】理解清楚题意,此题实际考查的是一个直径为8cm的圆内接正六边形的边长.
【解答】解:解:已知圆内接半径r为4cm,
则OB=4cm,
∴BD=OB sin30°=4×=2(cm).
则BC=2×2=4(cm).
故选C.
【点评】此题考查了多边形的计算,所求结果比较新颖,要注意题目问题的真正含义,即求圆内接正六边形的边长.
10.(2016 开平区一模)如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.
B.2
C.
D.3
【分析】延长AB,然后作出过点C与格点所在的直线,一定交于格点E,根据S△ABC=S△AEC﹣S△BEC即可求解.
【解答】解:延长AB,然后作出过点C与格点所在的直线,一定交于格点E.
正六边形的边长为1,则半径是1,则CE=4,
中间间隔一个顶点的两个顶点之间的距离是:,则△BCE的边EC上的高是:,
△ACE边EC上的高是:,
则S△ABC=S△AEC﹣S△BEC=×4×(﹣)=2.
故选:B.
【点评】本题考查了正多边形的计算,正确理解S△ABC=S△AEC﹣S△BEC是关键.
二.填空题(共4小题)
11.(2016 嘉定区一模)如果一个正多边形的中心角为72°,那么这个正多边形的边数是 5 .
【分析】根据正多边形的中心角和为360°和正多边形的中心角相等,列式计算即可.
【解答】解:根据题意得:
这个多边形的边数是360°÷72°=5,
故答案为:5.
【点评】本题考查的是正多边形的中心角的有关计算,掌握正多边形的中心角和边数的关系是解题的关键.
12.(2016 新县校级模拟)如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为 4﹣ .
【分析】首先得到当点E旋转至y轴上时DE最小,然后分别求得AD、OE′的长,最后求得DE′的长即可.
【解答】解:如图,当点E旋转至y轴上时DE最小;
∵△ABC是等边三角形,D为BC的中点,
∴AD⊥BC
∵AB=BC=2
∴AD=AB sin∠B=,
∵正六边形的边长等于其半径,正六边形的边长为2,
∴OE=OE′=2
∵点A的坐标为(0,6)
∴OA=6
∴DE′=OA﹣AD﹣OE′=4﹣;
故答案是:4﹣.
【点评】本题考查了正多边形的计算及等边三角形的性质,解题的关键是从图形中整理出直角三角形.
13.(2016 平度市一模)如图,圆内接正六边形ABCDEF的周长为12cm,则该正六边形的边心距为 cm.
【分析】首先得出正六边形的边长,构建直角三角形,利用直角三角形的边角关系即可求出.
【解答】解:连接OA,作OM⊥AB,得到∠AOM=30°,
∵圆内接正六边形ABCDEF的周长为12cm,
∴AB=2cm,则AM=1cm,
因而OM=OA cos30°=cm.
正六边形的边心距是cm.
故答案为:.
【点评】此题主要考查了正多边形和圆,正确掌握正六边形的性质是解题关键.
14.(2016 南江县校级模拟)半径为4的正n边形边心距为2,则此正n边形的边数为 6 .
【分析】由三角函数求出∠DAO=60°,得出∠AOD=30°,求出中心角∠AOB=60°,即可得出答案.
【解答】解:如图所示AB为正n边形的边长,OA为半径,OD为边心距,
∵半径为4的正n边形边心距为2,
∴sin∠DAO===,
∴∠DAO=60°,
∴∠AOD=30°,
∴∠AOB=60°,
∴n==6.
故答案为:6.
【点评】此题主要考查了正多边形和圆的有关计算,根据已知得出中心角∠AOB=60°是解题关键.
三.解答题(共6小题)
15.(2014 余姚市校级模拟)如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
【分析】连接BD,构造△DBE,然后证出△DBE∽△FCE,列出=,计算FC即可.
【解答】解:连接BD.
∵CE=×1=,
∴BE==,
在Rt△ABD中,BD==,
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴=,
∴=,
∴FC=.
【点评】本题考查了正多边形和圆,相似三角形的判定和性质,作出适当辅助线,得到相似三角形是解题的关键.
16.(2014 江西模拟)如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
【分析】(1)利用已知得出正八边形,它的内角都为135°,再利用正八边形ABCDEFGH关于直线BF对称,得出∠2+∠3=180°,进而得出答案;
(2)根据题意得出△PAH≌△QCB≌△MDE,则PA=QB=QC=MD.即PQ=QM,故四边形PQMN是正方形,进而求出PQ的长即可得出答案.
【解答】解:(1)连接BF,则有BF∥AG.
理由如下:
∵ABCDEFGH是正八边形,
∴它的内角都为135°.
又∵HA=HG,
∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°.
由于正八边形ABCDEFGH关于直线BF对称,
∴
即∠2+∠3=180°,故BF∥AG.
(2)根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形.
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD.即PQ=QM,
故四边形PQMN是正方形.
在Rt△PAB中,∵∠PAH=45°,AB=2,
∴,
∴.
故.
【点评】此题主要考查了正多边形和圆以及全等三角形的判定与性质等知识,得出PQ的长是解题关键.
17.(2014 碑林区校级模拟)如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为 2x+2 .
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
【分析】(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出;
(2)根据对角线相等且互相平分的四边形是矩形,顺次连接矩形的四个顶点即可作出;
(3)连接AC,利用相似三角形的性质求得DG的长,则BC和EF即可利用x和r表示出来,从而得到L关于x的函数关系式,利用二次函数的性质求解.
【解答】解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
△ABC就是所求的三角形;
(2)在直角△ABD中,AD==,
则BC=AD=,CD=AB=x.
则矩形的周长是:2x+2,
故答案是:2x+2;
(3)连接AC,
∵AD是直径,
∴∠ACD=90°,
又∵CG⊥AD于点G.
∴CD2=DG AD,
∴DG==,
∴BC=EF=AD﹣2DG=2r﹣.
则L=4x+4r﹣.
当x=﹣=r时,L取得最大值.最大值是:6r.
【点评】此题考查了正多边形和圆的知识.题目难度不大,利用x和半径r表示出BD和EF的长度是关键.
18.(2014秋 天台县期末)探究题:
(1) 各个角 都相等, 各条边 都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上,请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有 9 条对角线,它的外角和为 360 度.
【分析】(1)直接用正多边形的定义得出结论即可;
(2)用网格线的特征和正六边形的性质,画出图形即可;
(3)根据多边形的对角线条数的确定方法和多边形的外角和定理即可.
【解答】解:(1)由正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;
故答案为:各个角;各条边;
(2)如图,
∵AB=2,BC=2,CD=2,DE=2,EF=2,FA=2,
∴AB=BC=CD=DE=EF=FA,
∵网格是等边三角形的网格,
∴∠FAB=2×60°=120°,
同理:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴六边形ABCDEFA是正六边形.
最大面积为24;
(3)正六边形的对角线条数为=9,
∵多边形的外角和是360°,
∴正六边形的外角和为360°,
故答案为:9;360°.
【点评】此题是正多边形和圆,主要考查了正多边形的定义,正六边形的性质,网格线的特点,多边形的对角线的确定和多边形的外角和定理,解本题的关键掌握正六边形的性质.
19.(2014秋 吴江市校级期中)如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
【分析】首先连接OB,OC,OD,由等边△ABC内接于⊙O,BD为内接正十二边形的一边,可求得∠BOC,∠BOD的度数,继而证得△COD是等腰直角三角形,继而求得答案.
【解答】解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD cos45°=5×=5(cm).
即⊙O的半径R=5cm.
【点评】此题考查了正多边形与圆以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
20.(2014秋 渠县校级期中)如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
①求这个正六边形的边长.
②求这个正六边形的边心距.
③设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
【分析】(1)根据题意和正六边形的性质求出正六边形的边长;
(2)求出正六边形的中心角,根据正弦的概念解答即可;
(3)根据题意画出图形,根据圆的面积公式计算即可.
【解答】解:(1)∵正三角形的边长为6cm,
∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2;
(2)连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB==60°,
∴△OAB是等边三角形,
∴OD=OA sin60°=2×=;
(3)如图2:
线段AB划过的面积=π×22﹣π×()2=πcm2.
【点评】本题考查的是正多边形和圆的有关计算,正多边形的半径:外接圆的半径叫做正多边形的半径.中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.边心距:中心到正多边形的一边的距离叫做正多边形的边心距,正确运用三角函数或勾股定理进行计算是解题的关键.
第1页(共1页)
一.选择题(共10小题)
1.(2016 曲靖)如图,AD,BE,CF是正六边形ABCDEF的对角线,图中平行四边形的个数有( )
A.2个
B.4个
C.6个
D.8个
2.(2016 泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.
B.
C.
D.
3.(2016 南京)已知正六边形的边长为2,则它的内切圆的半径为( )
A.1
B.
C.2
D.2
4.(2016 南平)若正六边形的半径长为4,则它的边长等于( )
A.4
B.2
C.2
D.4
5.(2016 东平县二模)已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
6.(2016 湘潭一模)已知正三角形外接圆半径为2,这个正三角形的边长是( )
A.2
B.
C.3
D.2
7.(2016 南开区一模)正六边形的边心距与边长之比为( )
A.1:2
B.:2
C.:1
D.:2
8.(2016 宜昌模拟)正三角形内切圆与外接圆半径之比为( )
A.
B.
C.
D.
9.(2016 普陀区二模)如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
A.2cm
B.2cm
C.4cm
D.4Cm
10.(2016 开平区一模)如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.
B.2
C.
D.3
二.填空题(共4小题)
11.(2016 嘉定区一模)如果一个正多边形的中心角为72°,那么这个正多边形的边数是______.
12.(2016 新县校级模拟)如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为______.
13.(2016 平度市一模)如图,圆内接正六边形ABCDEF的周长为12cm,则该正六边形的边心距为______cm.
14.(2016 南江县校级模拟)半径为4的正n边形边心距为2,则此正n边形的边数为______.
三.解答题(共6小题)
15.(2014 余姚市校级模拟)如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
16.(2014 江西模拟)如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
17.(2014 碑林区校级模拟)如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为______.
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
18.(2014秋 天台县期末)探究题:
(1)______都相等,______都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上,请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有______条对角线,它的外角和为______度.
19.(2014秋 吴江市校级期中)如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
20.(2014秋 渠县校级期中)如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
①求这个正六边形的边长.
②求这个正六边形的边心距.
③设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 曲靖)如图,AD,BE,CF是正六边形ABCDEF的对角线,图中平行四边形的个数有( )
A.2个
B.4个
C.6个
D.8个
【分析】根据正六边形的性质,直接判断即可;
【解答】解:如图,
∵AD,BE,CF是正六边形ABCDEF的对角线,
∴OA=OE=AF=EF,
∴四边形AOEF是平行四边形,
同理:四边形DEFO,四边形ABCO,四边形BCDO,四边形CDEO,四边形FABOD都是平行四边形,共6个,
故选C
【点评】此题是正多边形和圆,主要考查了正六边形的性质,平行四边形的判定,掌握平行四边形的判定是解本题的关键.注意:数平行四边形个数时,按顺时针或逆时针数.
2.(2016 泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.
B.
C.
D.
【分析】由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
【解答】解:如图1,
∵OC=1,
∴OD=1×sin30°=;
如图2,
∵OB=1,
∴OE=1×sin45°=;
如图3,
∵OA=1,
∴OD=1×cos30°=,
则该三角形的三边分别为:、、,
∵()2+()2=()2,
∴该三角形是以、为直角边,为斜边的直角三角形,
∴该三角形的面积是××=,
故选:D.
【点评】本题主要考查多边形与圆,解答此题要明确:多边形的半径、边心距、中心角等概念,根据解直角三角形的知识解答是解题的关键.
3.(2016 南京)已知正六边形的边长为2,则它的内切圆的半径为( )
A.1
B.
C.2
D.2
【分析】根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
【解答】解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA sin60°=2×=,
∴边长为2的正六边形的内切圆的半径为.
故选B.
【点评】本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算,记住基本概念是解题的关键,属于中考常考题型.
4.(2016 南平)若正六边形的半径长为4,则它的边长等于( )
A.4
B.2
C.2
D.4
【分析】根据正六边形的外接圆半径和正六边形的边长将组成一个等边三角形,即可求解.
【解答】解:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,
故正六边形的半径等于4,则正六边形的边长是4.
故选:A.
【点评】此题主要考查了正多边形和圆,利用正六边形的外接圆半径和正六边形的边长将组成一个等边三角形得出是解题关键.
5.(2016 东平县二模)已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
【分析】过中心作边的垂线,连接半径,把内切圆半径,外接圆半径和高,中心角之间的计转化为解直角三角形.
【解答】解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选D.
【点评】正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径,外接圆半径和高,中心角之间的计转化为解直角三角形.
6.(2016 湘潭一模)已知正三角形外接圆半径为2,这个正三角形的边长是( )
A.2
B.
C.3
D.2
【分析】易得正三角形的中心角为120°,那么中心角的一半为60°,利用60°的正弦值可得正三角形边长的一半,乘以2即为正三角形的边长.
【解答】解:如图OA=2,求AB长.
∠AOB=360°÷3=120°
连接OA,OB,作OC⊥AB于点C,
∵OA=OB,
∴AB=2AC,∠AOC=60°,
∴AC=OA×sin60°=cm,
∴AB=2AC=2cm,
故选A.
【点评】考查有关正多边形和圆的相关计算;利用垂径定理和相应的三角函数知识得到AC的值是解决本题
的关键.
7.(2016 南开区一模)正六边形的边心距与边长之比为( )
A.1:2
B.:2
C.:1
D.:2
【分析】首先根据题意画出图形,然后设六边形的边长是a,由勾股定理即可求得OC的长,继而求得答案.
【解答】解:如图:设正六边形的边长是a,则半径长也是a;
经过正六边形的中心O作边AB的垂线段OC,则AC=AB=a,
于是OC==a,
所以正六边形的边心距与边长之比为:a:a=:2.
故选:D.
【点评】此题考查了正多边形和圆的关系.此题难度不大,注意掌握数形结合思想的应用.
8.(2016 宜昌模拟)正三角形内切圆与外接圆半径之比为( )
A.
B.
C.
D.
【分析】先作出图形,根据等边三角形的性质确定它的内切圆和外接圆的圆心;通过特殊角进行计算,用内切圆半径来表示外接圆半径,最后求出比值即可.
【解答】解:如图,△ABC是等边三角形,AD是高.点O是其外接圆的圆心,由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BO=2OD,而OA=OB,
∴OD:OA=1:2.
故选A.
【点评】本题考查的是正多边形和圆,熟知等边三角形的性质及三角形内切圆与外接圆的定义是解答此题的关键.
9.(2016 普陀区二模)如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
A.2cm
B.2cm
C.4cm
D.4Cm
【分析】理解清楚题意,此题实际考查的是一个直径为8cm的圆内接正六边形的边长.
【解答】解:解:已知圆内接半径r为4cm,
则OB=4cm,
∴BD=OB sin30°=4×=2(cm).
则BC=2×2=4(cm).
故选C.
【点评】此题考查了多边形的计算,所求结果比较新颖,要注意题目问题的真正含义,即求圆内接正六边形的边长.
10.(2016 开平区一模)如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A.
B.2
C.
D.3
【分析】延长AB,然后作出过点C与格点所在的直线,一定交于格点E,根据S△ABC=S△AEC﹣S△BEC即可求解.
【解答】解:延长AB,然后作出过点C与格点所在的直线,一定交于格点E.
正六边形的边长为1,则半径是1,则CE=4,
中间间隔一个顶点的两个顶点之间的距离是:,则△BCE的边EC上的高是:,
△ACE边EC上的高是:,
则S△ABC=S△AEC﹣S△BEC=×4×(﹣)=2.
故选:B.
【点评】本题考查了正多边形的计算,正确理解S△ABC=S△AEC﹣S△BEC是关键.
二.填空题(共4小题)
11.(2016 嘉定区一模)如果一个正多边形的中心角为72°,那么这个正多边形的边数是 5 .
【分析】根据正多边形的中心角和为360°和正多边形的中心角相等,列式计算即可.
【解答】解:根据题意得:
这个多边形的边数是360°÷72°=5,
故答案为:5.
【点评】本题考查的是正多边形的中心角的有关计算,掌握正多边形的中心角和边数的关系是解题的关键.
12.(2016 新县校级模拟)如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为 4﹣ .
【分析】首先得到当点E旋转至y轴上时DE最小,然后分别求得AD、OE′的长,最后求得DE′的长即可.
【解答】解:如图,当点E旋转至y轴上时DE最小;
∵△ABC是等边三角形,D为BC的中点,
∴AD⊥BC
∵AB=BC=2
∴AD=AB sin∠B=,
∵正六边形的边长等于其半径,正六边形的边长为2,
∴OE=OE′=2
∵点A的坐标为(0,6)
∴OA=6
∴DE′=OA﹣AD﹣OE′=4﹣;
故答案是:4﹣.
【点评】本题考查了正多边形的计算及等边三角形的性质,解题的关键是从图形中整理出直角三角形.
13.(2016 平度市一模)如图,圆内接正六边形ABCDEF的周长为12cm,则该正六边形的边心距为 cm.
【分析】首先得出正六边形的边长,构建直角三角形,利用直角三角形的边角关系即可求出.
【解答】解:连接OA,作OM⊥AB,得到∠AOM=30°,
∵圆内接正六边形ABCDEF的周长为12cm,
∴AB=2cm,则AM=1cm,
因而OM=OA cos30°=cm.
正六边形的边心距是cm.
故答案为:.
【点评】此题主要考查了正多边形和圆,正确掌握正六边形的性质是解题关键.
14.(2016 南江县校级模拟)半径为4的正n边形边心距为2,则此正n边形的边数为 6 .
【分析】由三角函数求出∠DAO=60°,得出∠AOD=30°,求出中心角∠AOB=60°,即可得出答案.
【解答】解:如图所示AB为正n边形的边长,OA为半径,OD为边心距,
∵半径为4的正n边形边心距为2,
∴sin∠DAO===,
∴∠DAO=60°,
∴∠AOD=30°,
∴∠AOB=60°,
∴n==6.
故答案为:6.
【点评】此题主要考查了正多边形和圆的有关计算,根据已知得出中心角∠AOB=60°是解题关键.
三.解答题(共6小题)
15.(2014 余姚市校级模拟)如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
【分析】连接BD,构造△DBE,然后证出△DBE∽△FCE,列出=,计算FC即可.
【解答】解:连接BD.
∵CE=×1=,
∴BE==,
在Rt△ABD中,BD==,
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴=,
∴=,
∴FC=.
【点评】本题考查了正多边形和圆,相似三角形的判定和性质,作出适当辅助线,得到相似三角形是解题的关键.
16.(2014 江西模拟)如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
【分析】(1)利用已知得出正八边形,它的内角都为135°,再利用正八边形ABCDEFGH关于直线BF对称,得出∠2+∠3=180°,进而得出答案;
(2)根据题意得出△PAH≌△QCB≌△MDE,则PA=QB=QC=MD.即PQ=QM,故四边形PQMN是正方形,进而求出PQ的长即可得出答案.
【解答】解:(1)连接BF,则有BF∥AG.
理由如下:
∵ABCDEFGH是正八边形,
∴它的内角都为135°.
又∵HA=HG,
∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°.
由于正八边形ABCDEFGH关于直线BF对称,
∴
即∠2+∠3=180°,故BF∥AG.
(2)根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形.
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD.即PQ=QM,
故四边形PQMN是正方形.
在Rt△PAB中,∵∠PAH=45°,AB=2,
∴,
∴.
故.
【点评】此题主要考查了正多边形和圆以及全等三角形的判定与性质等知识,得出PQ的长是解题关键.
17.(2014 碑林区校级模拟)如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为 2x+2 .
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
【分析】(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出;
(2)根据对角线相等且互相平分的四边形是矩形,顺次连接矩形的四个顶点即可作出;
(3)连接AC,利用相似三角形的性质求得DG的长,则BC和EF即可利用x和r表示出来,从而得到L关于x的函数关系式,利用二次函数的性质求解.
【解答】解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
△ABC就是所求的三角形;
(2)在直角△ABD中,AD==,
则BC=AD=,CD=AB=x.
则矩形的周长是:2x+2,
故答案是:2x+2;
(3)连接AC,
∵AD是直径,
∴∠ACD=90°,
又∵CG⊥AD于点G.
∴CD2=DG AD,
∴DG==,
∴BC=EF=AD﹣2DG=2r﹣.
则L=4x+4r﹣.
当x=﹣=r时,L取得最大值.最大值是:6r.
【点评】此题考查了正多边形和圆的知识.题目难度不大,利用x和半径r表示出BD和EF的长度是关键.
18.(2014秋 天台县期末)探究题:
(1) 各个角 都相等, 各条边 都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上,请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有 9 条对角线,它的外角和为 360 度.
【分析】(1)直接用正多边形的定义得出结论即可;
(2)用网格线的特征和正六边形的性质,画出图形即可;
(3)根据多边形的对角线条数的确定方法和多边形的外角和定理即可.
【解答】解:(1)由正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;
故答案为:各个角;各条边;
(2)如图,
∵AB=2,BC=2,CD=2,DE=2,EF=2,FA=2,
∴AB=BC=CD=DE=EF=FA,
∵网格是等边三角形的网格,
∴∠FAB=2×60°=120°,
同理:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴六边形ABCDEFA是正六边形.
最大面积为24;
(3)正六边形的对角线条数为=9,
∵多边形的外角和是360°,
∴正六边形的外角和为360°,
故答案为:9;360°.
【点评】此题是正多边形和圆,主要考查了正多边形的定义,正六边形的性质,网格线的特点,多边形的对角线的确定和多边形的外角和定理,解本题的关键掌握正六边形的性质.
19.(2014秋 吴江市校级期中)如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
【分析】首先连接OB,OC,OD,由等边△ABC内接于⊙O,BD为内接正十二边形的一边,可求得∠BOC,∠BOD的度数,继而证得△COD是等腰直角三角形,继而求得答案.
【解答】解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD cos45°=5×=5(cm).
即⊙O的半径R=5cm.
【点评】此题考查了正多边形与圆以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
20.(2014秋 渠县校级期中)如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
①求这个正六边形的边长.
②求这个正六边形的边心距.
③设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
【分析】(1)根据题意和正六边形的性质求出正六边形的边长;
(2)求出正六边形的中心角,根据正弦的概念解答即可;
(3)根据题意画出图形,根据圆的面积公式计算即可.
【解答】解:(1)∵正三角形的边长为6cm,
∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2;
(2)连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB==60°,
∴△OAB是等边三角形,
∴OD=OA sin60°=2×=;
(3)如图2:
线段AB划过的面积=π×22﹣π×()2=πcm2.
【点评】本题考查的是正多边形和圆的有关计算,正多边形的半径:外接圆的半径叫做正多边形的半径.中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.边心距:中心到正多边形的一边的距离叫做正多边形的边心距,正确运用三角函数或勾股定理进行计算是解题的关键.
第1页(共1页)
