3.2.3互斥事件
图片预览




文档简介
课件17张PPT。3.2.3互斥事件潼关中学 关学智温故知新古典概型
概率公式1、试验的所有结果只有有限个且每次只有一个结果。
2、每一个试验结果出现的可能性相同。古典概型
概率公式古典概型
概率公式古典概型两个特征:古典概型
概率公式古典概型
概率公式 一般来说,在建立概率模型时把什么看作是基本事件,即试验结果是人为规定的,也就是说,对于同一个随机试验,可以根据需要,建立满我们要求的概率模型
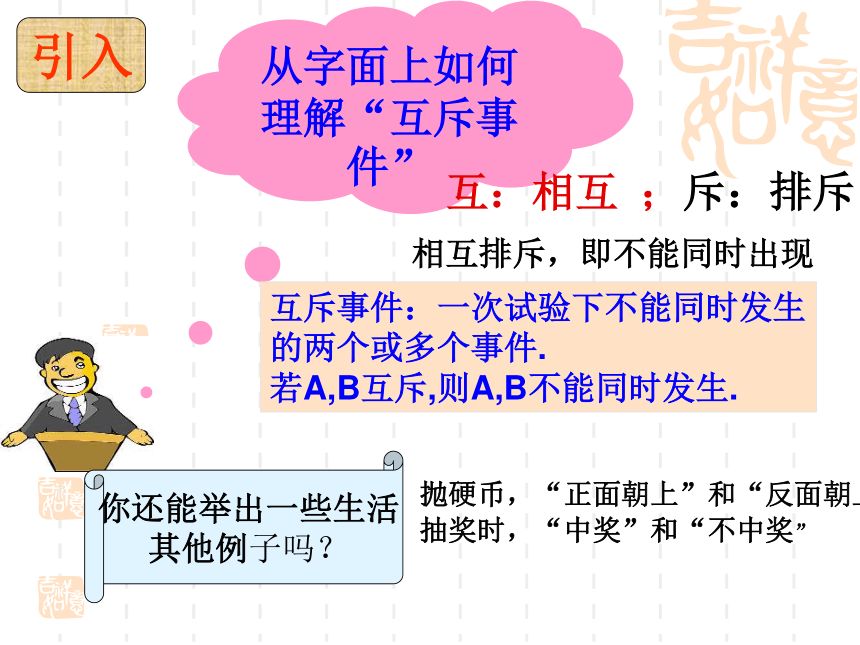
概率模型从字面上如何理解“互斥事件”互:相互 ;斥:排斥互斥事件:一次试验下不能同时发生
的两个或多个事件.
若A,B互斥,则A,B不能同时发生.相互排斥,即不能同时出现引入你还能举出一些生活
其他例子吗?抛硬币,“正面朝上”和“反面朝上”
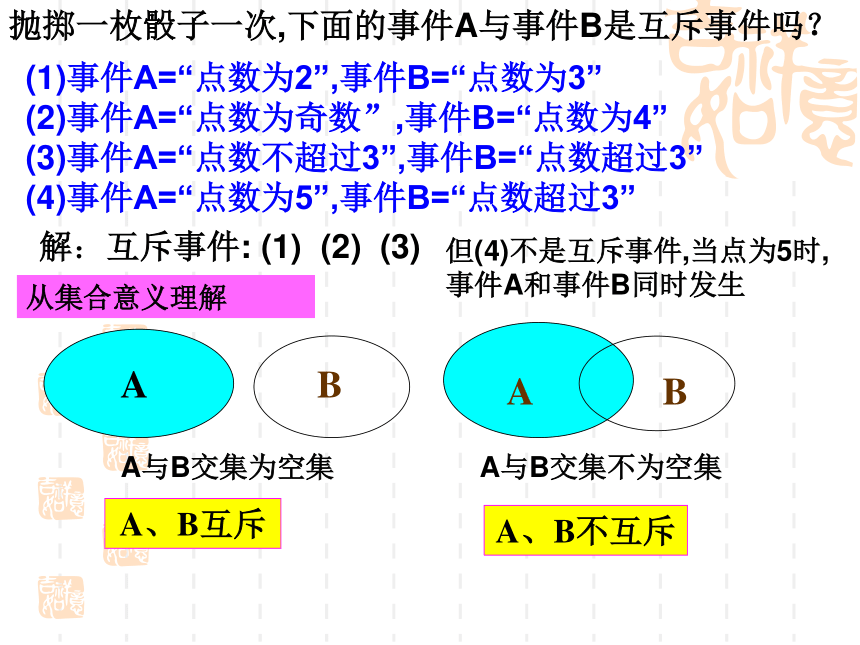
抽奖时,“中奖”和“不中奖”抛掷一枚骰子一次,下面的事件A与事件B是互斥事件吗?(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
(4)事件A=“点数为5”,事件B=“点数超过3”解:互斥事件: (1) (2) (3)A、B互斥A、B不互斥从集合意义理解但(4)不是互斥事件,当点为5时,
事件A和事件B同时发生A与B交集为空集A与B交集不为空集(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
(4)事件A=“点数为5”,事件B=“点数超过3”在(1)中,A表示事件“点数为2”,B表示事件”点数为3”,
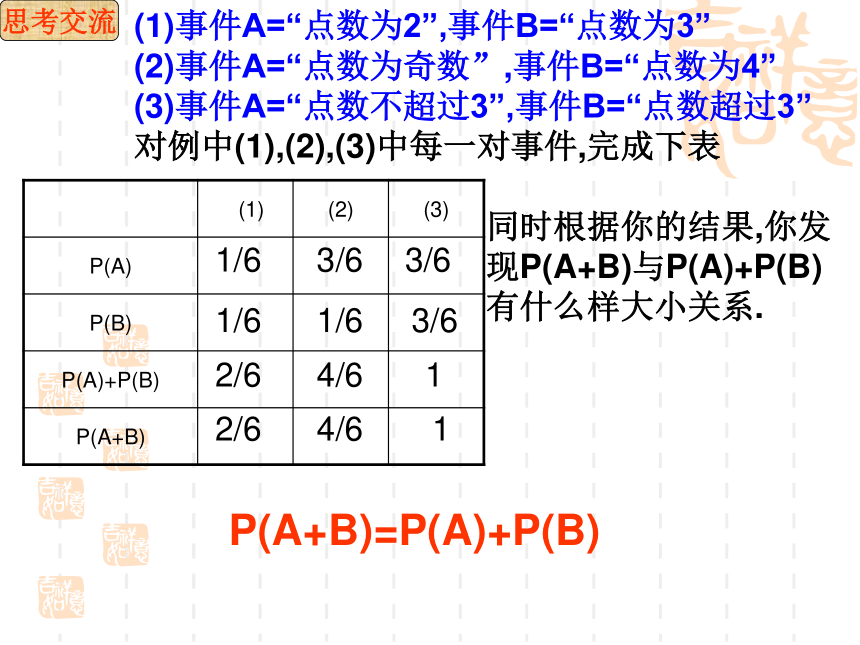
我们把事件“点数为2或3”记作A+B事件A+B发生的意义:事件A和事件B中至少有一个发生当A与B互斥时,A+B事件指“A发生B不发生”和“A不发生B发生”(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
对例中(1),(2),(3)中每一对事件,完成下表思考交流同时根据你的结果,你发
现P(A+B)与P(A)+P(B)
有什么样大小关系.P(A+B)=P(A)+P(B)1/61/62/62/63/61/64/64/63/63/611抽象概括在一个随机事试验中,如果事件A和事件B是互斥事件,那么P(A+B)=P(A)+P(B)(概率加法公式)一般地,如果事件A1,A2,…,An彼此互斥,那么事件发生(即A1,A2,…,An中有一个发生)的概率,等于这n个事件分别发生的概率的和,即拓展推广P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)
自己阅读课本第144页 例4
从一箱新产品中随机地抽取一件新产品,设A=“抽到的是一等品”B=“抽到的是二等品”,C=“抽到的是三等品”,且P(A)=0.7,P(B)=0.1,P(C)=0.05.求下列事件的概率. 自主学习⑴事件D=“抽到的是一等品或三等品”⑵事件E=“抽到的是二等品或三等品”(1)事件A=“点数为2”,事件B=“点数3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”思考交流1/61/62/62/63/61/64/64/63/63/611在(3)中,我们发现有P(A+B)=P(A)+P(B)=1概率为1,说明事件A+B必然事件,即A和B中必有一个发生此时,我们把事件B称为事件A的对立事件。(4)事件A=“点数为5”,
事件B=“点数超过3”在(4)中,P(A+B)=P(A)+P(B)?概率加法公式:
P(A+B)=P(A)+P(B),
只适用于互斥事件对立事件:必有一个发生的两个彼此互斥的事件 (也称互逆事件)抽象理解但是互斥未必是对立事件对立事件一定是互斥事件例如:事件“点数为奇数”和“点数为4”从集合的意义上来看对立事件:
1、A与 的交集为空集 2、A+ 为事件全体,为必然事件。互斥事件:不同时发生的两个或多个事件
对立事件:必有一个发生的两个彼此互斥的事件互斥事件P(A+B) = P(A) + P(B)对立事件P(A)=1-P(B)=1-对立事件一定是互斥事件,但互斥未必是对立事件概率公式:事件A1,A2,…,An彼此互斥P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)2. 对飞机连续射击两次,每次发射一枚炮弹,记事件A:两次都击中飞机.事件B:两次都没有击中飞机. 事件C:恰有一次击中飞机.事件D:至少有一次击中飞机.其中互斥事件是 .A与B,A与C,B与C,B与D0.34、经统计,在某储蓄所一个营业窗口等候的人数为及相应概率如下:
(1)至多1人排队等候的概率是多少?
(2)有人排队等候的概率是多少?1、将一枚质地均匀的硬币先后抛3次,恰好出现一次正面朝上的概率 。3/8(1)至少3人排队等候的概率是多少?
(2) 有人排队等候的概率是多少?解:记“有0人等候”为事件A,“有1人等候”为事件B,“有2人等候”
为事件C,“有3人等候”为事件D,“有4人等候”为事件E,“有5人
及至5人以上等候”为事件F,则易知A,B,C,D,E,F互斥(2)记“有人排队等候”为事件H,(1)“记至少3人排除等候”为事件G,
P(G)=P(D+E+F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44不能少P(H)=1-P( )=1-0.1=0.9记“没有排除等候”事件⑴求他参加不超过2个小组的概率
⑵求他至少参加了2个小组的概率解(1)用事件A表示“选取的成员参加不超过2个小组”用A1表示“选取成员只参加1个小组”,A2“选取成员只参加2个小组”,A1与A2互斥事件例题分析:从图中可以看出,3个兴趣小组总人数:6+7+8+11+10+10=60有时当多事件A比较
复杂,可以通过A的
对立事件求,可能
会简单点 经验之谈表达要清晰,
不可少P(A)=P(A1+A2)=课本
P146例6用事件 表示“选取的成员参加了3个小组” P(A)=1-P( )=1- ≈0.87P(B)=1-P( )=1- ≈0.6(2)用事件B表示“选取的成员至少参加2个小组”
则 表示“选取的成员只参加1个小组”(1)分析先由树状图得出取出的2张卡片的所有情况P146 例823145解法1 解法2 解法3 如果我们不考虑抽取的顺序,而只看结果[1,2] [1,3] [1,4] [1,5] [2,3]
[2,4] [2,5] [3,4] [3,5] [4,5]例如:[2,4]表示“取出的2人是2号和4号”同学们自己排出所有结果⑵分析:用列表法列出所有结果解法1:用A1表示事件“取出的2人中恰有一位女生”,A2表示事
件“取出的2人都是女生”则A1和A2互斥解法2 用A表示事件“取出的2人全是男生”,则 表示
“取出的2人不全是男生”思考交流P(A+B) = P(A) + P(B) 小结:事件A1,A2,…,An彼此互斥P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)互斥事件:不同时发生的两个或多个事件若事件A与B互斥:对立事件:必有一个发生的两个互斥事件P(A)=1-P(B)=1-
概率公式1、试验的所有结果只有有限个且每次只有一个结果。
2、每一个试验结果出现的可能性相同。古典概型
概率公式古典概型
概率公式古典概型两个特征:古典概型
概率公式古典概型
概率公式 一般来说,在建立概率模型时把什么看作是基本事件,即试验结果是人为规定的,也就是说,对于同一个随机试验,可以根据需要,建立满我们要求的概率模型
概率模型从字面上如何理解“互斥事件”互:相互 ;斥:排斥互斥事件:一次试验下不能同时发生
的两个或多个事件.
若A,B互斥,则A,B不能同时发生.相互排斥,即不能同时出现引入你还能举出一些生活
其他例子吗?抛硬币,“正面朝上”和“反面朝上”
抽奖时,“中奖”和“不中奖”抛掷一枚骰子一次,下面的事件A与事件B是互斥事件吗?(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
(4)事件A=“点数为5”,事件B=“点数超过3”解:互斥事件: (1) (2) (3)A、B互斥A、B不互斥从集合意义理解但(4)不是互斥事件,当点为5时,
事件A和事件B同时发生A与B交集为空集A与B交集不为空集(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
(4)事件A=“点数为5”,事件B=“点数超过3”在(1)中,A表示事件“点数为2”,B表示事件”点数为3”,
我们把事件“点数为2或3”记作A+B事件A+B发生的意义:事件A和事件B中至少有一个发生当A与B互斥时,A+B事件指“A发生B不发生”和“A不发生B发生”(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
对例中(1),(2),(3)中每一对事件,完成下表思考交流同时根据你的结果,你发
现P(A+B)与P(A)+P(B)
有什么样大小关系.P(A+B)=P(A)+P(B)1/61/62/62/63/61/64/64/63/63/611抽象概括在一个随机事试验中,如果事件A和事件B是互斥事件,那么P(A+B)=P(A)+P(B)(概率加法公式)一般地,如果事件A1,A2,…,An彼此互斥,那么事件发生(即A1,A2,…,An中有一个发生)的概率,等于这n个事件分别发生的概率的和,即拓展推广P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)
自己阅读课本第144页 例4
从一箱新产品中随机地抽取一件新产品,设A=“抽到的是一等品”B=“抽到的是二等品”,C=“抽到的是三等品”,且P(A)=0.7,P(B)=0.1,P(C)=0.05.求下列事件的概率. 自主学习⑴事件D=“抽到的是一等品或三等品”⑵事件E=“抽到的是二等品或三等品”(1)事件A=“点数为2”,事件B=“点数3”
(2)事件A=“点数为奇数”,事件B=“点数为4”
(3)事件A=“点数不超过3”,事件B=“点数超过3”思考交流1/61/62/62/63/61/64/64/63/63/611在(3)中,我们发现有P(A+B)=P(A)+P(B)=1概率为1,说明事件A+B必然事件,即A和B中必有一个发生此时,我们把事件B称为事件A的对立事件。(4)事件A=“点数为5”,
事件B=“点数超过3”在(4)中,P(A+B)=P(A)+P(B)?概率加法公式:
P(A+B)=P(A)+P(B),
只适用于互斥事件对立事件:必有一个发生的两个彼此互斥的事件 (也称互逆事件)抽象理解但是互斥未必是对立事件对立事件一定是互斥事件例如:事件“点数为奇数”和“点数为4”从集合的意义上来看对立事件:
1、A与 的交集为空集 2、A+ 为事件全体,为必然事件。互斥事件:不同时发生的两个或多个事件
对立事件:必有一个发生的两个彼此互斥的事件互斥事件P(A+B) = P(A) + P(B)对立事件P(A)=1-P(B)=1-对立事件一定是互斥事件,但互斥未必是对立事件概率公式:事件A1,A2,…,An彼此互斥P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)2. 对飞机连续射击两次,每次发射一枚炮弹,记事件A:两次都击中飞机.事件B:两次都没有击中飞机. 事件C:恰有一次击中飞机.事件D:至少有一次击中飞机.其中互斥事件是 .A与B,A与C,B与C,B与D0.34、经统计,在某储蓄所一个营业窗口等候的人数为及相应概率如下:
(1)至多1人排队等候的概率是多少?
(2)有人排队等候的概率是多少?1、将一枚质地均匀的硬币先后抛3次,恰好出现一次正面朝上的概率 。3/8(1)至少3人排队等候的概率是多少?
(2) 有人排队等候的概率是多少?解:记“有0人等候”为事件A,“有1人等候”为事件B,“有2人等候”
为事件C,“有3人等候”为事件D,“有4人等候”为事件E,“有5人
及至5人以上等候”为事件F,则易知A,B,C,D,E,F互斥(2)记“有人排队等候”为事件H,(1)“记至少3人排除等候”为事件G,
P(G)=P(D+E+F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44不能少P(H)=1-P( )=1-0.1=0.9记“没有排除等候”事件⑴求他参加不超过2个小组的概率
⑵求他至少参加了2个小组的概率解(1)用事件A表示“选取的成员参加不超过2个小组”用A1表示“选取成员只参加1个小组”,A2“选取成员只参加2个小组”,A1与A2互斥事件例题分析:从图中可以看出,3个兴趣小组总人数:6+7+8+11+10+10=60有时当多事件A比较
复杂,可以通过A的
对立事件求,可能
会简单点 经验之谈表达要清晰,
不可少P(A)=P(A1+A2)=课本
P146例6用事件 表示“选取的成员参加了3个小组” P(A)=1-P( )=1- ≈0.87P(B)=1-P( )=1- ≈0.6(2)用事件B表示“选取的成员至少参加2个小组”
则 表示“选取的成员只参加1个小组”(1)分析先由树状图得出取出的2张卡片的所有情况P146 例823145解法1 解法2 解法3 如果我们不考虑抽取的顺序,而只看结果[1,2] [1,3] [1,4] [1,5] [2,3]
[2,4] [2,5] [3,4] [3,5] [4,5]例如:[2,4]表示“取出的2人是2号和4号”同学们自己排出所有结果⑵分析:用列表法列出所有结果解法1:用A1表示事件“取出的2人中恰有一位女生”,A2表示事
件“取出的2人都是女生”则A1和A2互斥解法2 用A表示事件“取出的2人全是男生”,则 表示
“取出的2人不全是男生”思考交流P(A+B) = P(A) + P(B) 小结:事件A1,A2,…,An彼此互斥P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)互斥事件:不同时发生的两个或多个事件若事件A与B互斥:对立事件:必有一个发生的两个互斥事件P(A)=1-P(B)=1-
