2010年中考第二轮复习专题六函数与几何综合应用
文档属性
| 名称 | 2010年中考第二轮复习专题六函数与几何综合应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 242.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-19 00:00:00 | ||
图片预览




文档简介
§7.函数与几何综合应用
例1.【06海南中考】如图1,已知二次函数图象的顶点坐标为C(1,0),直线与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴上.
(1)求的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为,点P的横坐标为,求与之间的函数关系式,并写出自变量的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
解:(1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m. ∴ m=1.
设所求二次函数的关系式为y=a(x-1)2
∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
∴ 4=a(3-1)2, ∴ a=1.
∴ 所求二次函数的关系式为y=(x-1)2.
即y=x2-2x+1.
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE =(x+1)-(x2-2x+1)=-x2+3x.
即h=-x2+3x (0<x<3).
(3) 存在.
解法1:要使四边形DCEP是平行四边形,必需有PE=DC.
∵ 点D在直线y=x+1上,∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .即x2-3x+2=0 .
解之,得 x1=2,x2=1 (不合题意,舍去)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.
例2.【07海南中考】如图,直线与轴交于点,与轴交于点,已知二次函数的图象经过点、和点.
(1)求该二次函数的关系式;
(2)设该二次函数的图象的顶点为,求四边形的面积;
(3)有两动点、同时从点出发,其中点以每秒个单位长
度的速度沿折线 按→→的路线运动,点以每秒
个单位长度的速度沿折线按→→的路线运动,当、
两点相遇时,它们都停止运动.设、同时从点出发秒时,
的面积为S .
①请问、两点在运动过程中,是否存在∥,若存在,请求出此时的值;若不存在,请说明理由;
②请求出S关于的函数关系式,并写出自变量的取值范围;
③设是②中函数S的最大值,那么 = .
解:(1)令,则;令则.∴、
∵二次函数的图象过点,∴可设二次函数的关系式为
又∵该函数图象过点、
∴ 解之,得,
∴所求二次函数的关系式为
(2)∵=
∴顶点M的坐标为 过点M作MF轴于F
∴
=
∴四边形AOCM的面积为10
(3)①不存在DE∥OC
∵若DE∥OC,则点D、E应分别在线段OA、CA上,此时 1设点E的坐标为∴,∴ ∵DE∥OC,
∴ ∴ ∵>2,不满足1②根据题意得D、E两点相遇的时间为(秒)
现分情况讨论如下:ⅰ当0 <≤ 1时,;
ⅱ当1<≤2时,设点E的坐标为
∴,∴
∴
ⅲ当2 <<时,设点E的坐标为,类似ⅱ可得
设点D的坐标为
∴,∴
∴= ③
例3.【08海南中考】如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:① CB=CE ;② D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,
使得PB=PE,若存在,试求出所有符合条件的点P的坐标;
若不存在,请说明理由.
解(1)∵ 点B(-2,m)在直线y=-2x-1上,∴ m=-2×(-2)-1=3.
∴ B(-2,3)∵ 抛物线经过原点O和点A,对称轴为x=2,
∴ 点A的坐标为(4,0) .
设所求的抛物线对应函数关系式为y=a(x-0)(x-4).
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4),∴ .
∴ 所求的抛物线对应的函数关系式为,即.
(2)①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4.
在Rt△BGC中,BC=.
∵ CE=5,∴ CB=CE=5.
②过点E作EH∥x轴,交y轴于H,
则点H的坐标为H(0,-5).
又点F、D的坐标为F(0,3)、D(0,-1),
∴ FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°.
∴ △DFB≌△DHE (SAS),∴ BD=DE.
即D是BE的中点.
(3) 存在.
由于PB=PE,∴ 点P在直线CD上,
∴ 符合条件的点P是直线CD与该抛物线的交点.
设直线CD对应的函数关系式为y=kx+b.
将D(0,-1) C(2,0)代入,得. 解得 .
∴ 直线CD对应的函数关系式为y=x-1.
∵ 动点P的坐标为(x,),∴ x-1=.
解得 ,. ∴ ,.
∴ 符合条件的点P的坐标为(,)或(,).
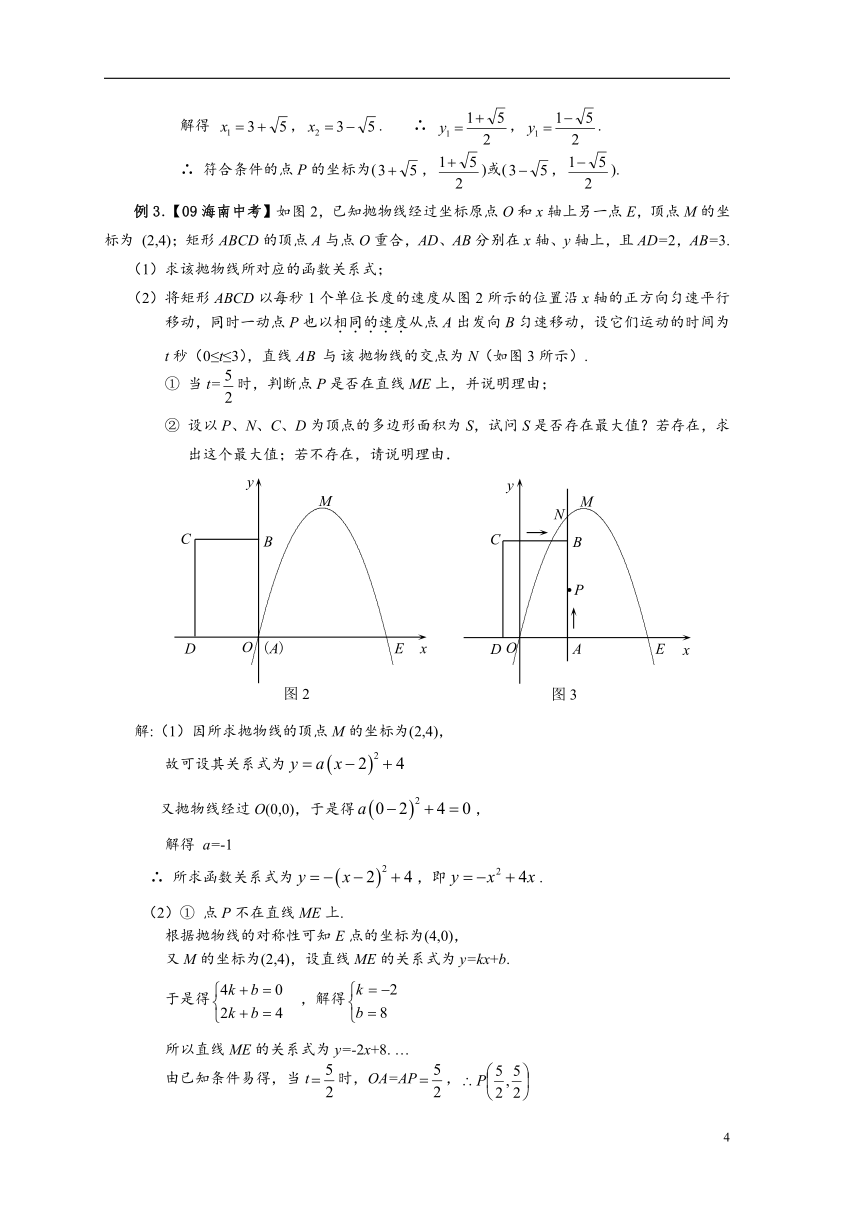
例3.【09海南中考】如图2,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图2所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图3所示).
① 当t=时,判断点P是否在直线ME上,并说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
解:(1)因所求抛物线的顶点M的坐标为(2,4),
故可设其关系式为
又抛物线经过O(0,0),于是得,
解得 a=-1
∴ 所求函数关系式为,即.
(2)① 点P不在直线ME上.
根据抛物线的对称性可知E点的坐标为(4,0),
又M的坐标为(2,4),设直线ME的关系式为y=kx+b.
于是得 ,解得
所以直线ME的关系式为y=-2x+8. …
由已知条件易得,当t时,OA=AP,
∵ P点的坐标不满足直线ME的关系式y=-2x+8.
∴ 当t时,点P不在直线ME上.
② S存在最大值. 理由如下:
∵ 点A在x轴的非负半轴上,且N在抛物线上, ∴ OA=AP=t.
∴ 点P,N的坐标分别为(t,t)、(t,-t 2+4t) ∴ AN=-t 2+4t (0≤t≤3) ,
∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴ S=DC·AD=×3×2=3. …………
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=(CD+PN)·AD=[3+(-t 2+3 t)]×2=-t 2+3 t+3=
其中(0<t<3),由a=-1,0<<3,此时. …
综上所述,当t时,以点P,N,C,D为顶点的多边形面积有最大值,
这个最大值为. …………
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.
☆基础达标演练☆
一、解答题
1.(09黑龙江佳木斯)如图,抛物线经过两点,此抛物线的对称轴为直线,顶点为,且与直线交于点.
(1)求此抛物线的解析式;
(2)直接写出此抛物线的对称轴和顶点坐标;
(3)连接,求证:;
2.(09四川达州)如图1,抛物线与轴相交于A、B两点(点A在点B右侧),过点A的直线交抛物线于另一点C,点C的坐标为(-2,6).
(1)求a的值及直线AC的函数关系式;
(2)P是线段AC上一动点,过点P作y轴的平行线,交抛物线于点M,交x轴于点N.
①求线段PM长度的最大值;
②在抛物线上是否存在这样的点M,使得△CMP与△APN相似?如果存在,请直接写出所有满足条件的点M的坐标(不必写解答过程);如果不存在,请说明理由.
3.(09四川广安)已知:抛物线与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?若存在,求出最大值并求此时D点坐标;若不存在,请说明理由.
4.(09福建龙岩)如图,抛物线与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由. ( http: / / www. / )
5.(09河南)如图,在平面直角坐标系中,已知矩形的三个顶点、、.抛物线过两点.
(1)直接写出点的坐标,并求出抛物线的解析式;
(2)动点从点出发,沿线段向终点运动,同时点从点出发,沿线段向终点运动,速度均为每秒1个单位长度,运动时间为秒.过点作交于点.
①过点作于点,交抛物线于点.当为何值时,线段最长?
②连接.在点运动的过程中,判断有几个时刻使得是等腰三角形?
请直接写出相应的值.
6.(09湖南长沙)如图,二次函数()的图象与轴交于两点,与轴相交于点.连结两点的坐标分别为、,且当和时二次函数的函数值相等.
(1)求实数的值;
(2)若点同时从点出发,均以每秒1个单位长度的速度分别沿边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为秒时,连结,将沿翻折,点恰好落在边上的处,求的值及点的坐标;
(3)在(2)的条件下,二次函数图象的对称轴上是否存在点,使得以为项点的三角形与相似?如果存在,请求出点的坐标;如果不存在,请说明理由.
7.(09江西)如图,抛物线与轴相交于、两点(点在点的左侧),与轴相交于点,顶点为.
(1)直接写出、、三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;
①用含的代数式表示线段的长,并求出当为何值时,四边形为平行四边形?
②设的面积为,求与的函数关系式.
8.(09辽宁本溪)如图所示,在平面直角坐标系中,抛物线()经过,,三点,其顶点为,连接,点是线段上一个动点(不与重合),过点作轴的垂线,垂足为,连接.
(1)求抛物线的解析式,并写出顶点的坐标;
(2)如果点的坐标为,的面积为,求与的函数关系式,写出自变量的取值范围,并求出的最大值;
(3)在(2)的条件下,当取得最大值时,过点作的垂线,垂足为,连接,把 沿直线折叠,点的对应点为,请直接写出点坐标,并判断点是否在该抛物线上.
9.(09山东济南)已知:抛物线的对称轴为与轴交于 两点,与轴交于点其中、
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得的周长最小.请求出点P的坐标.
(3)若点是线段上的一个动点(不与点O、点C重合).过点D作交轴于点连接、.设的长为,的面积为.求与之间的函数关系式.试说明是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
10.(09浙江湖州)已知抛物线()与轴相交于点,顶点为.直线分别与轴,轴相交于两点,并且与直线相交于点.
(1)填空:试用含的代数式分别表示点与的坐标,则;
(2)如图,将沿轴翻折,若点的对应点′恰好落在抛物线上,′与轴交于点,连结,求的值和四边形的面积;
(3)在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,试说明理由.
G
Q
D
F
A
x
O
y
A
l
x
y
C
B
P
E
B
O
A
C
D
y
x
A
M
P
B
N
C
x
O
y
DO
CO
BO
O
☆海南中考典例精析☆
E
D
O
C
B
A
D
y
x
O
图1
P
C
A
B
E
x
y
x=2
G
F
H
y
x
E
D
O
C
B
A
图3
B
C
O
A
D
E
M
y
x
P
N
·
图2
B
C
O
(A)
D
E
M
y
x
y
x
B
D
O
A
E
C
D
A
B
C
F
E
H
O
y
x
1
2
3
3
1
D
y
C
B
A
P
2
E
x
O
A
C
x
y
B
O
第(2)题
x
y
B
C
O
D
A
M
N
N′
x
y
B
C
O
A
M
N
备用图
PAGE
1
例1.【06海南中考】如图1,已知二次函数图象的顶点坐标为C(1,0),直线与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴上.
(1)求的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为,点P的横坐标为,求与之间的函数关系式,并写出自变量的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
解:(1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m. ∴ m=1.
设所求二次函数的关系式为y=a(x-1)2
∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
∴ 4=a(3-1)2, ∴ a=1.
∴ 所求二次函数的关系式为y=(x-1)2.
即y=x2-2x+1.
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE =(x+1)-(x2-2x+1)=-x2+3x.
即h=-x2+3x (0<x<3).
(3) 存在.
解法1:要使四边形DCEP是平行四边形,必需有PE=DC.
∵ 点D在直线y=x+1上,∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .即x2-3x+2=0 .
解之,得 x1=2,x2=1 (不合题意,舍去)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.
例2.【07海南中考】如图,直线与轴交于点,与轴交于点,已知二次函数的图象经过点、和点.
(1)求该二次函数的关系式;
(2)设该二次函数的图象的顶点为,求四边形的面积;
(3)有两动点、同时从点出发,其中点以每秒个单位长
度的速度沿折线 按→→的路线运动,点以每秒
个单位长度的速度沿折线按→→的路线运动,当、
两点相遇时,它们都停止运动.设、同时从点出发秒时,
的面积为S .
①请问、两点在运动过程中,是否存在∥,若存在,请求出此时的值;若不存在,请说明理由;
②请求出S关于的函数关系式,并写出自变量的取值范围;
③设是②中函数S的最大值,那么 = .
解:(1)令,则;令则.∴、
∵二次函数的图象过点,∴可设二次函数的关系式为
又∵该函数图象过点、
∴ 解之,得,
∴所求二次函数的关系式为
(2)∵=
∴顶点M的坐标为 过点M作MF轴于F
∴
=
∴四边形AOCM的面积为10
(3)①不存在DE∥OC
∵若DE∥OC,则点D、E应分别在线段OA、CA上,此时 1
∴ ∴ ∵>2,不满足1
现分情况讨论如下:ⅰ当0 <≤ 1时,;
ⅱ当1<≤2时,设点E的坐标为
∴,∴
∴
ⅲ当2 <<时,设点E的坐标为,类似ⅱ可得
设点D的坐标为
∴,∴
∴= ③
例3.【08海南中考】如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:① CB=CE ;② D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,
使得PB=PE,若存在,试求出所有符合条件的点P的坐标;
若不存在,请说明理由.
解(1)∵ 点B(-2,m)在直线y=-2x-1上,∴ m=-2×(-2)-1=3.
∴ B(-2,3)∵ 抛物线经过原点O和点A,对称轴为x=2,
∴ 点A的坐标为(4,0) .
设所求的抛物线对应函数关系式为y=a(x-0)(x-4).
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4),∴ .
∴ 所求的抛物线对应的函数关系式为,即.
(2)①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4.
在Rt△BGC中,BC=.
∵ CE=5,∴ CB=CE=5.
②过点E作EH∥x轴,交y轴于H,
则点H的坐标为H(0,-5).
又点F、D的坐标为F(0,3)、D(0,-1),
∴ FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°.
∴ △DFB≌△DHE (SAS),∴ BD=DE.
即D是BE的中点.
(3) 存在.
由于PB=PE,∴ 点P在直线CD上,
∴ 符合条件的点P是直线CD与该抛物线的交点.
设直线CD对应的函数关系式为y=kx+b.
将D(0,-1) C(2,0)代入,得. 解得 .
∴ 直线CD对应的函数关系式为y=x-1.
∵ 动点P的坐标为(x,),∴ x-1=.
解得 ,. ∴ ,.
∴ 符合条件的点P的坐标为(,)或(,).
例3.【09海南中考】如图2,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图2所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图3所示).
① 当t=时,判断点P是否在直线ME上,并说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
解:(1)因所求抛物线的顶点M的坐标为(2,4),
故可设其关系式为
又抛物线经过O(0,0),于是得,
解得 a=-1
∴ 所求函数关系式为,即.
(2)① 点P不在直线ME上.
根据抛物线的对称性可知E点的坐标为(4,0),
又M的坐标为(2,4),设直线ME的关系式为y=kx+b.
于是得 ,解得
所以直线ME的关系式为y=-2x+8. …
由已知条件易得,当t时,OA=AP,
∵ P点的坐标不满足直线ME的关系式y=-2x+8.
∴ 当t时,点P不在直线ME上.
② S存在最大值. 理由如下:
∵ 点A在x轴的非负半轴上,且N在抛物线上, ∴ OA=AP=t.
∴ 点P,N的坐标分别为(t,t)、(t,-t 2+4t) ∴ AN=-t 2+4t (0≤t≤3) ,
∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴ S=DC·AD=×3×2=3. …………
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=(CD+PN)·AD=[3+(-t 2+3 t)]×2=-t 2+3 t+3=
其中(0<t<3),由a=-1,0<<3,此时. …
综上所述,当t时,以点P,N,C,D为顶点的多边形面积有最大值,
这个最大值为. …………
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.
☆基础达标演练☆
一、解答题
1.(09黑龙江佳木斯)如图,抛物线经过两点,此抛物线的对称轴为直线,顶点为,且与直线交于点.
(1)求此抛物线的解析式;
(2)直接写出此抛物线的对称轴和顶点坐标;
(3)连接,求证:;
2.(09四川达州)如图1,抛物线与轴相交于A、B两点(点A在点B右侧),过点A的直线交抛物线于另一点C,点C的坐标为(-2,6).
(1)求a的值及直线AC的函数关系式;
(2)P是线段AC上一动点,过点P作y轴的平行线,交抛物线于点M,交x轴于点N.
①求线段PM长度的最大值;
②在抛物线上是否存在这样的点M,使得△CMP与△APN相似?如果存在,请直接写出所有满足条件的点M的坐标(不必写解答过程);如果不存在,请说明理由.
3.(09四川广安)已知:抛物线与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA
(2)求此抛物线的解析式;
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?若存在,求出最大值并求此时D点坐标;若不存在,请说明理由.
4.(09福建龙岩)如图,抛物线与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由. ( http: / / www. / )
5.(09河南)如图,在平面直角坐标系中,已知矩形的三个顶点、、.抛物线过两点.
(1)直接写出点的坐标,并求出抛物线的解析式;
(2)动点从点出发,沿线段向终点运动,同时点从点出发,沿线段向终点运动,速度均为每秒1个单位长度,运动时间为秒.过点作交于点.
①过点作于点,交抛物线于点.当为何值时,线段最长?
②连接.在点运动的过程中,判断有几个时刻使得是等腰三角形?
请直接写出相应的值.
6.(09湖南长沙)如图,二次函数()的图象与轴交于两点,与轴相交于点.连结两点的坐标分别为、,且当和时二次函数的函数值相等.
(1)求实数的值;
(2)若点同时从点出发,均以每秒1个单位长度的速度分别沿边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为秒时,连结,将沿翻折,点恰好落在边上的处,求的值及点的坐标;
(3)在(2)的条件下,二次函数图象的对称轴上是否存在点,使得以为项点的三角形与相似?如果存在,请求出点的坐标;如果不存在,请说明理由.
7.(09江西)如图,抛物线与轴相交于、两点(点在点的左侧),与轴相交于点,顶点为.
(1)直接写出、、三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;
①用含的代数式表示线段的长,并求出当为何值时,四边形为平行四边形?
②设的面积为,求与的函数关系式.
8.(09辽宁本溪)如图所示,在平面直角坐标系中,抛物线()经过,,三点,其顶点为,连接,点是线段上一个动点(不与重合),过点作轴的垂线,垂足为,连接.
(1)求抛物线的解析式,并写出顶点的坐标;
(2)如果点的坐标为,的面积为,求与的函数关系式,写出自变量的取值范围,并求出的最大值;
(3)在(2)的条件下,当取得最大值时,过点作的垂线,垂足为,连接,把 沿直线折叠,点的对应点为,请直接写出点坐标,并判断点是否在该抛物线上.
9.(09山东济南)已知:抛物线的对称轴为与轴交于 两点,与轴交于点其中、
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得的周长最小.请求出点P的坐标.
(3)若点是线段上的一个动点(不与点O、点C重合).过点D作交轴于点连接、.设的长为,的面积为.求与之间的函数关系式.试说明是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
10.(09浙江湖州)已知抛物线()与轴相交于点,顶点为.直线分别与轴,轴相交于两点,并且与直线相交于点.
(1)填空:试用含的代数式分别表示点与的坐标,则;
(2)如图,将沿轴翻折,若点的对应点′恰好落在抛物线上,′与轴交于点,连结,求的值和四边形的面积;
(3)在抛物线()上是否存在一点,使得以为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,试说明理由.
G
Q
D
F
A
x
O
y
A
l
x
y
C
B
P
E
B
O
A
C
D
y
x
A
M
P
B
N
C
x
O
y
DO
CO
BO
O
☆海南中考典例精析☆
E
D
O
C
B
A
D
y
x
O
图1
P
C
A
B
E
x
y
x=2
G
F
H
y
x
E
D
O
C
B
A
图3
B
C
O
A
D
E
M
y
x
P
N
·
图2
B
C
O
(A)
D
E
M
y
x
y
x
B
D
O
A
E
C
D
A
B
C
F
E
H
O
y
x
1
2
3
3
1
D
y
C
B
A
P
2
E
x
O
A
C
x
y
B
O
第(2)题
x
y
B
C
O
D
A
M
N
N′
x
y
B
C
O
A
M
N
备用图
PAGE
1
同课章节目录
