18.2.1 矩形的判定 课件
图片预览


文档简介
课件11张PPT。矩形的判定王雪峰 情境 小华利用周末的时间,找来两根长度相等的短木条和两根长度相等的长木条,为自己做了一个相框. 问题1 请你利用直尺和三角
板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有
其他判定矩形的方法呢? 生活剪影 温故知新 问题2 你还记得学习平行四边形的判定时,我们
是如何猜想并进行证明的吗? 探究猜想 同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
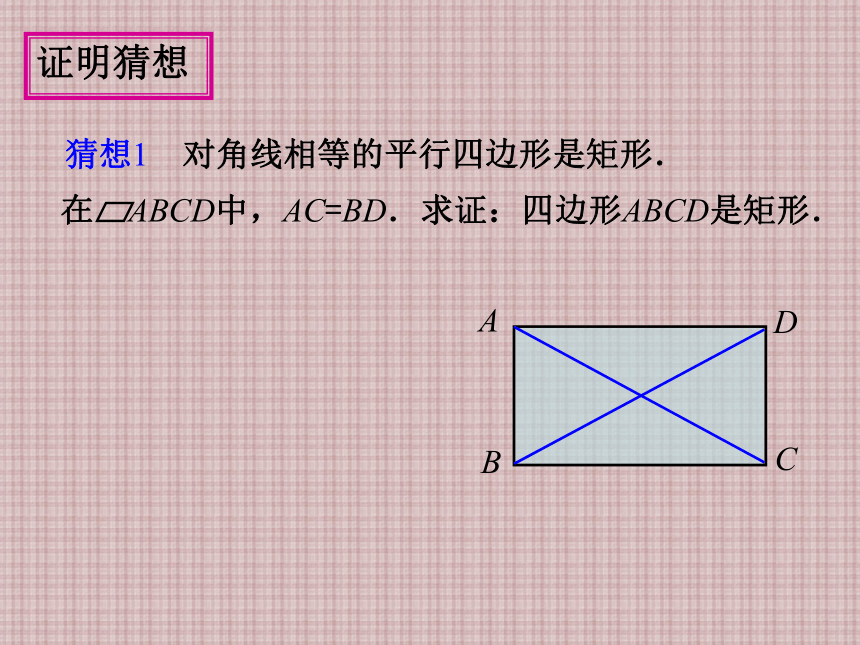
猜想1 对角线相等的平行四边形是矩形.
猜想2 三个角是直角的四边形是矩形.
问题3 如何证明这两个猜想?证明猜想 猜想1 对角线相等的平行四边形是矩形.证明猜想 猜想2 有三个角是直角的四边形是矩形. 在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.方法1:有一个角是直角的平行四边形叫做矩形;
方法2:对角线相等的平行四边形是矩形;
方法3:有三个角是直角的四边形是矩形.理一理 你能归纳矩形的判定方法吗? 练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都是直角的四边形是矩形;( )
(3)四个角都相等的四边形是矩形;( )
(4)对角线相等的四边形是矩形;( )
(5)对角线相等且互相垂直的四边形是矩形;( )
(6)对角线互相平分且相等的四边形是矩形;( )
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(8)两组对边分别平行,且对角线相等的四边形是矩形;( )
××√辩一辩 √×√√√用一用 例 如图,在 ABCD中,对角线AC,BD相交于点
O,且OA=OD,∠OAD=50°.求∠OAB的度数.理一理 练习2 在“?”号处填上恰当的条件: 一种学习方法
两个猜想证明
三种判定方法 理一理
板帮他检验一下,相框是矩形吗?
除了矩形的定义外,有没有
其他判定矩形的方法呢? 生活剪影 温故知新 问题2 你还记得学习平行四边形的判定时,我们
是如何猜想并进行证明的吗? 探究猜想 同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
猜想1 对角线相等的平行四边形是矩形.
猜想2 三个角是直角的四边形是矩形.
问题3 如何证明这两个猜想?证明猜想 猜想1 对角线相等的平行四边形是矩形.证明猜想 猜想2 有三个角是直角的四边形是矩形. 在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.方法1:有一个角是直角的平行四边形叫做矩形;
方法2:对角线相等的平行四边形是矩形;
方法3:有三个角是直角的四边形是矩形.理一理 你能归纳矩形的判定方法吗? 练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都是直角的四边形是矩形;( )
(3)四个角都相等的四边形是矩形;( )
(4)对角线相等的四边形是矩形;( )
(5)对角线相等且互相垂直的四边形是矩形;( )
(6)对角线互相平分且相等的四边形是矩形;( )
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(8)两组对边分别平行,且对角线相等的四边形是矩形;( )
××√辩一辩 √×√√√用一用 例 如图,在 ABCD中,对角线AC,BD相交于点
O,且OA=OD,∠OAD=50°.求∠OAB的度数.理一理 练习2 在“?”号处填上恰当的条件: 一种学习方法
两个猜想证明
三种判定方法 理一理
