沪科版八年级数学下册20.2数据的集中趋势与离散程度测试卷(含答案解析)
文档属性
| 名称 | 沪科版八年级数学下册20.2数据的集中趋势与离散程度测试卷(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 20:00:18 | ||
图片预览



文档简介
沪科版八年级数学下册20.2《数据的集中趋势与离散程度》
测
试
卷
一.选择题(共10小题)
1.(2016 桂林)一组数据7,8,10,12,13的平均数是( )
A.7
B.9
C.10
D.12
2.(2016 呼伦贝尔)从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A.
B.
C.
D.
3.(2016 宁阳县模拟)下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
4.(2016 冷水江市校级模拟)某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.﹣3.5
B.3
C.0.5
D.﹣3
5.(2016 临沂)某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
A.4
B.3
C.2
D.1
6.(2016 南宁)某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分
B.82分
C.84分
D.86分
7.(2016 柘城县一模)九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
A.1:2
B.2:1
C.2:3
D.3:2
8.(2016 曲靖)某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
A.极差是6
B.众数是10
C.平均数是9.5
D.方差是16
9.(2016 株洲)甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
队员
平均成绩
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34
A.甲
B.乙
C.丙
D.丁
10.(2016 湖北襄阳)一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2
二.填空题(共4小题)
11.(2016 东营)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是______.
12.(2016 金华)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是______mg/L.
13.(2016 大连)下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是______岁.
14.(2016 大庆)甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是______(填“甲”或“乙”).
三.解答题(共6小题)
15.(2014秋 曹县期末)设一组数据x1,x2,…,xn的平均数为m,求下列各组数据的平均数:
(1)x1+3,x2+3,…,xn+3;
(2)2x1,2x2,…,2xn.
16.(2013秋 莘县期中)某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期
一
二
三
四
五
六
日
增减/辆
8
5
﹣2
﹣7
﹣6
10
13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
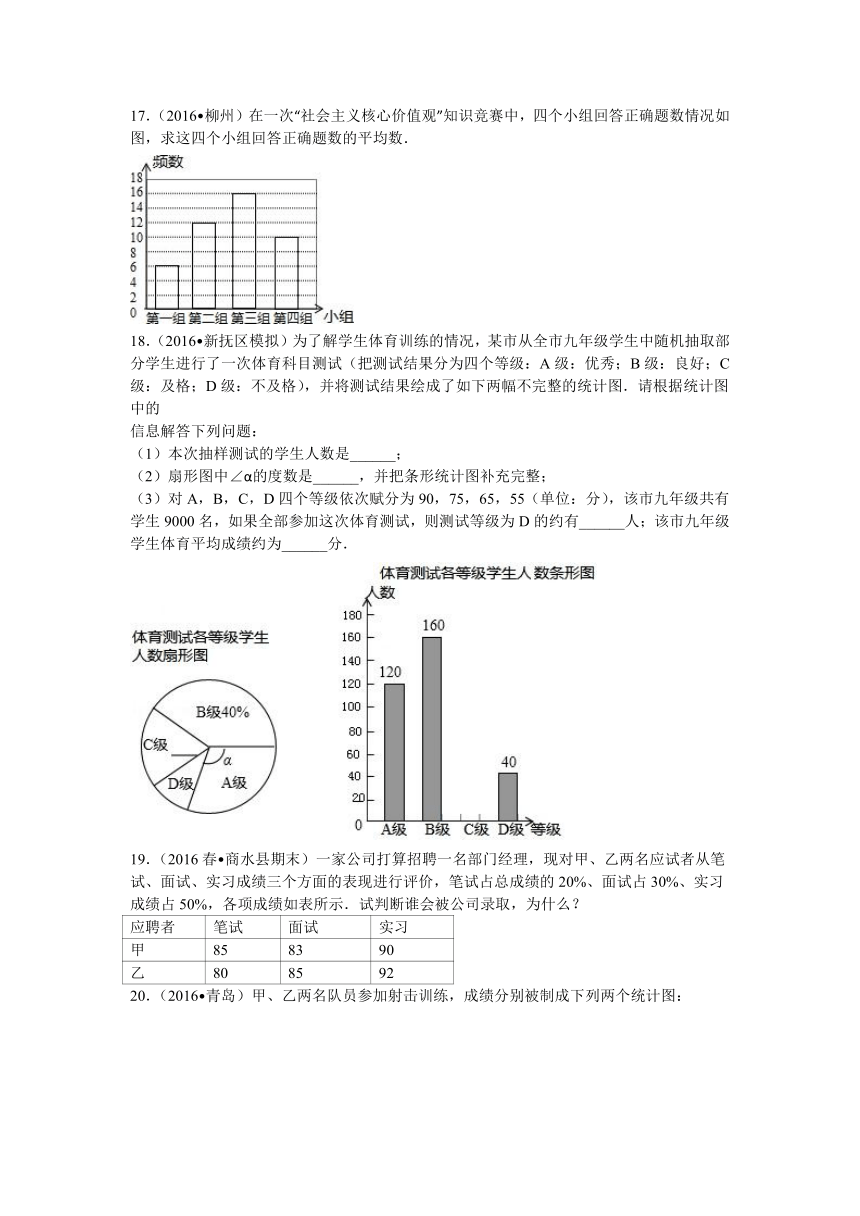
17.(2016 柳州)在一次“社会主义核心价值观”知识竞赛中,四个小组回答正确题数情况如图,求这四个小组回答正确题数的平均数.
18.(2016 新抚区模拟)为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的
信息解答下列问题:
(1)本次抽样测试的学生人数是______;
(2)扇形图中∠α的度数是______,并把条形统计图补充完整;
(3)对A,B,C,D四个等级依次赋分为90,75,65,55(单位:分),该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有______人;该市九年级学生体育平均成绩约为______分.
19.(2016春 商水县期末)一家公司打算招聘一名部门经理,现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价,笔试占总成绩的20%、面试占30%、实习成绩占50%,各项成绩如表所示.试判断谁会被公司录取,为什么?
应聘者
笔试
面试
实习
甲
85
83
90
乙
80
85
92
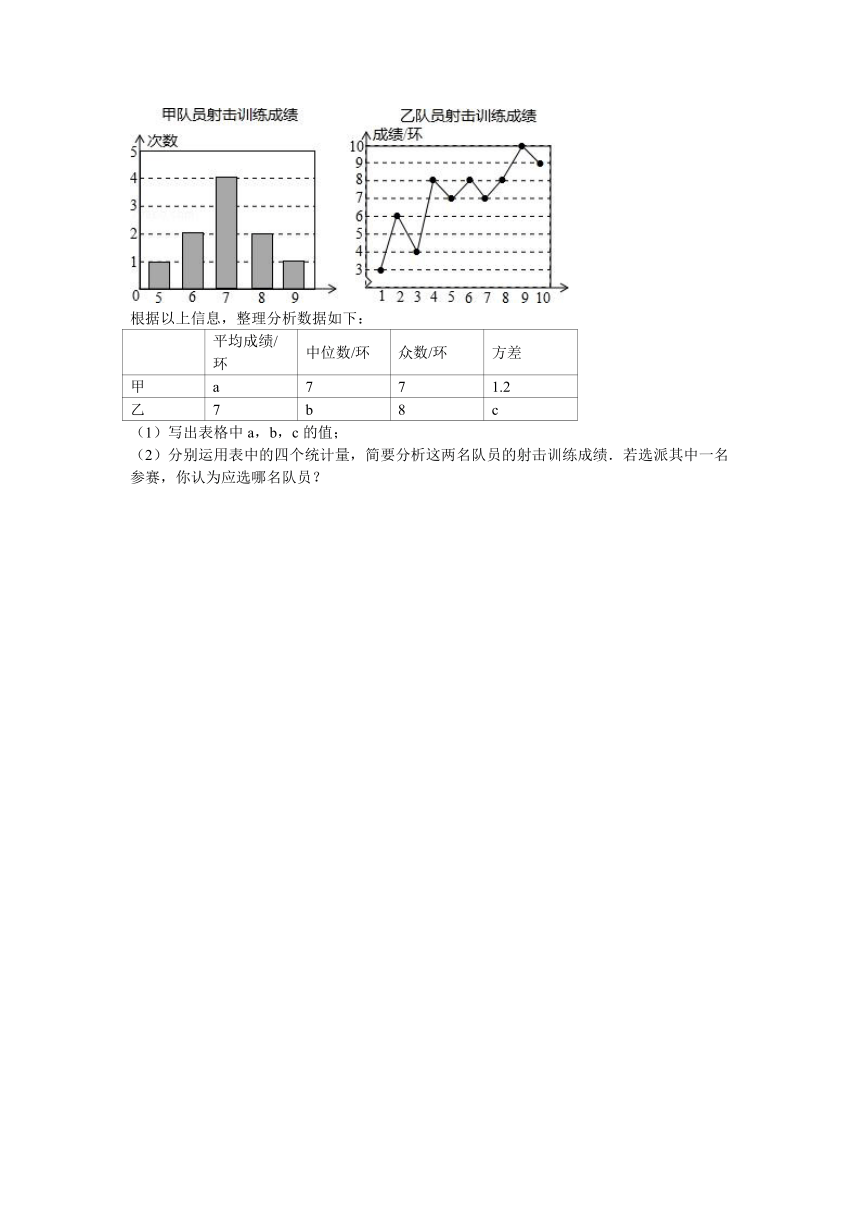
20.(2016 青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
参考答案与试题解析
一.选择题(共10小题)
1.(2016 桂林)一组数据7,8,10,12,13的平均数是( )
A.7
B.9
C.10
D.12
【分析】根据平均数的定义:平均数是指在一组数据中所有数据之和再除以数据的个数进行计算即可.
【解答】解:(7+8+10+12+13)÷5
=50÷5
=10
答:一组数据7,8,10,12,13的平均数是10.
故选:C.
【点评】本题考查了平均数的知识,掌握一组数据平均数的求解方法是解题关键.
2.(2016 呼伦贝尔)从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A.
B.
C.
D.
【分析】根据平均数的公式,求解即可.用所有数据的和除以(a+b+c).
【解答】解:由题意知,a个x1的和为ax1,b个x2的和为bx2,c个x3的和为cx3,数据总共有a+b+c个,
∴这个样本的平均数=,
故选:B.
【点评】本题考查了加权平均数的概念.平均数等于所有数据的和除以数据的个数.
3.(2016 宁阳县模拟)下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
【分析】运用平均数,中位数,众数的概念采用排除法即可解.
【解答】解:A、数据3,4,4,7,3的众数是4和3.故错误;
B、数据0,1,2,5,a的中位数因a的大小不确定,故中位数也无法确定.故错误;
C、一组数据的众数和中位数会出现相等的情况.故错误;
D、数据0,5,﹣7,﹣5,7的中位数和平数数都是0.对.
故选D.
【点评】本题重点考查平均数,中位数,众数的概念及求法.
4.(2016 冷水江市校级模拟)某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.﹣3.5
B.3
C.0.5
D.﹣3
【分析】根据题意可以得到求出的平均数与实际平均数之间的差值,本题得以解决.
【解答】解:∵(105﹣15)÷30=90÷30=3,
∴求出的平均数与实际平均数的差是﹣3,
故选D.
【点评】本题考查算术平均数,解题的关键是明确算术平均数的计算方法.
5.(2016 临沂)某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
A.4
B.3
C.2
D.1
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.本题利用加权平均数的公式即可求解.
【解答】解:根据题意得:
(1×1+2×2+4×3+2×4+1×5)÷10=3(小时),
答:这10名学生周末学均时间是3小时;
故选B.
【点评】此题考查了加权平均数,本题易出现的错误是求1,2,4,2,1这五个数的平均数,对平均数的理解不正确.
6.(2016 南宁)某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分
B.82分
C.84分
D.86分
【分析】利用加权平均数的公式直接计算即可得出答案.
【解答】解:
由加权平均数的公式可知===86,
故选D.
【点评】本题主要考查加权平均数的计算,掌握加权平均数的公式=是解题的关键.
7.(2016 柘城县一模)九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
A.1:2
B.2:1
C.2:3
D.3:2
【分析】设男生是x人,女生是y人,然后根据加权平均数公式列方程求解.
【解答】解:设男生是x人,女生是y人,
根据题意得:=80,
则82x+77y=80x+80y,即2x=3y,
则x:y=3:2.
故选D.
【点评】本题考查了加权平均数公式,数据的权能够反映数据的相对“重要程度”,要突出某个数据,只需要给它较大的“权”,权的差异对结果会产生直接的影响.(4)对于一组不同权重的数据,加权平均数更能反映数据的真实信息,理解公式是关键.
8.(2016 曲靖)某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
A.极差是6
B.众数是10
C.平均数是9.5
D.方差是16
【分析】极差是指一组数据中最大数据与最小数据的差;一组数据中出现次数最多的数据叫做众数;平均数是指在一组数据中所有数据之和再除以数据的个数;一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.
【解答】解:(A)极差为11﹣6=5,故(A)错误;
(B)根据出现次数最多的数据是10可得,众数是10,故(B)正确;
(C)平均数为(10+6+9+11+8+10)÷6=9,故(C)错误;
(D)方差为[(10﹣9)2+(6﹣9)2+(9﹣9)2+(11﹣9)2+(8﹣9)2+(10﹣9)2]=,故(D)错误.
故选(B)
【点评】本题主要考查了极差、众数、平均数以及方差的计算,注意:极差只能反映数据的波动范围,众数反映了一组数据的集中程度,平均数是反映数据集中趋势的一项指标,方差是反映一组数据的波动大小的一个量.
9.(2016 株洲)甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
队员
平均成绩
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34
A.甲
B.乙
C.丙
D.丁
【分析】首先比较平均数,然后比较方差,方差越小,越稳定.
【解答】解:∵==9.7,S2甲>S2乙,
∴选择丙.
故选C.
【点评】此题考查了方差的知识.注意方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
10.(2016 湖北襄阳)一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2
【分析】先根据平均数的定义求出x的值,再根据众数、中位数的定义和方差公式分别进行解答即可.
【解答】解:根据题意,=3,解得:x=3,
∴这组数据从小到大排列为:2,3,3,3,4;
则这组数据的中位数为3,
这组数据3出现的次数最多,出现了3次,故众数为3;
其方差是:×[(2﹣3)2+3×(3﹣3)2+(4﹣3)2]=0.4,
故选A.
【点评】本题考查了众数、中位数和方差,众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
二.填空题(共4小题)
11.(2016 东营)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是 101 .
【分析】根据算术平均数的计算公式列式计算即可得解.
【解答】解:=(102+115+100+105+92+105+85+104)=×808=101.
故答案为:101.
【点评】本题考查了算术平均数,是基础题,准确计算是解题的关键.
12.(2016 金华)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是 1 mg/L.
【分析】根据题意可以求得这6次总的含量,由折线统计图可以得到除第3次的含量,从而可以得到第3次检测得到的氨氮含量.
【解答】解:由题意可得,
第3次检测得到的氨氮含量是:1.5×6﹣(1.6+2+1.5+1.4+1.5)=9﹣8=1mg/L,
故答案为:1.
【点评】本题考查算术平均数、折线统计图,解题的关键是明确题意,找出所求问题需要的条件.
13.(2016 大连)下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是 15 岁.
【分析】根据加权平均数的计算公式列出算式,再进行计算即可.
【解答】解:根据题意得:
(13×1+14×1+15×7+16×3)÷12=15(岁),
即该校女子排球队队员的平均年龄为15岁.
故答案为:15.
【点评】此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键.
14.(2016 大庆)甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是 甲 (填“甲”或“乙”).
【分析】计算出乙的平均数和方差后,与甲的方差比较后,可以得出判断.
【解答】解:乙组数据的平均数=(0+1+5+9+10)÷5=5,
乙组数据的方差S2=[(0﹣5)2+(1﹣5)2+(9﹣5)2+(10﹣5)2]=16.4,
∵S2甲<S2乙,
∴成绩较为稳定的是甲.
故答案为:甲.
【点评】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
三.解答题(共6小题)
15.(2014秋 曹县期末)设一组数据x1,x2,…,xn的平均数为m,求下列各组数据的平均数:
(1)x1+3,x2+3,…,xn+3;
(2)2x1,2x2,…,2xn.
【分析】首先根据求平均数的公式:=,得出x1+x2+…+xn,再利用此公式求出(1)x1+3,x2+3,…,xn+3以及(2)2x1,2x2,…,2xn的平均数.
【解答】解:设一组数据x1,x2,…,xn的平均数是m,
即=,
则x1+x2+…+xn=mn.
(1)∵x1+x2+…+xn=mn,
∴x1+3+x2+3+…+xn+3=mn+3n,
∴x1+3,x2+3,…,xn+3的平均数是=m+3;
(2)∵x1+x2+…+xn=mn,
∴2x1+2x2+…+2xn=2mn,
∴2x1,2x2,…,2xn的平均数是=2m.
【点评】本题考查的是样本平均数的求法及运用,熟记平均数公式是解题的关键.
16.(2013秋 莘县期中)某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期
一
二
三
四
五
六
日
增减/辆
8
5
﹣2
﹣7
﹣6
10
13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
【分析】(1)读统计图,直接回答;
(2)根据平均数的概念计算.
【解答】解:(1)从统计表格中得出星期四经过红绿灯路口的小汽车最少,为93辆;星期日经过红绿灯路口的小汽车最多,为113辆;
(2)平均数=(8+5﹣2﹣7﹣6+10+13)÷7+100=103,
故平均每天有103辆小汽车通过这个红绿灯路口.
答:(1)星期四最少,为93辆;星期日最多,为113辆;
(2)平均每天有103辆小汽车通过这个红绿灯路口.
【点评】本题考查了从统计表格得出信息的能力和计算平均数的能力.
17.(2016 柳州)在一次“社会主义核心价值观”知识竞赛中,四个小组回答正确题数情况如图,求这四个小组回答正确题数的平均数.
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.
【解答】解:(6+12+16+10)÷4
=44÷4
=11
∴这四个小组回答正确题数的平均数是11.
【点评】此题主要考查了平均数的含义和求法,以及条形统计图的应用,要熟练掌握.
18.(2016 新抚区模拟)为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的
信息解答下列问题:
(1)本次抽样测试的学生人数是 400 ;
(2)扇形图中∠α的度数是 108° ,并把条形统计图补充完整;
(3)对A,B,C,D四个等级依次赋分为90,75,65,55(单位:分),该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有 900 人;该市九年级学生体育平均成绩约为 75.5 分.
【分析】(1)根据B级的人数和百分比求出学生人数;
(2)求出A级的百分比,360°乘百分比即为∠α的度数,根据各等级人数之和等于总人数求出C等级人数,补全条形图;
(3)根据样本中D等级所占比例乘以总人数9000可得,运用加权平均数的求法即可求出九年级学生体育平均成绩.
【解答】解:(1)本次抽样测试的学生人数是:160÷40%=400,
故答案为:400;
(2)扇形图中∠α的度数是:×360°=108°,
C等级人数为:400﹣120﹣160﹣40=80(人),补全条形图如图:
故答案为:108°;
(3)测试等级为D的约有×9000=900(人),
学生体育平均成绩约为:90×+75×+65×+55×=75.5(分),
故答案为:900,75.5.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,扇形统计图直接反映部分占总体的百分比大小.
19.(2016春 商水县期末)一家公司打算招聘一名部门经理,现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价,笔试占总成绩的20%、面试占30%、实习成绩占50%,各项成绩如表所示.试判断谁会被公司录取,为什么?
应聘者
笔试
面试
实习
甲
85
83
90
乙
80
85
92
【分析】首先根据加权平均数的计算方法,分别求出甲、乙的平均成绩各是多少;然后比较大小,判断出谁会被公司录取即可.
【解答】解:甲的平均成绩为:
85×20%+83×30%+90×50%
=17+24.9+45
=86.9
乙的平均成绩为:
80×20%+85×30%+92×50%
=16+25.5+46
=87.5
∵87.5>86.9,
∴乙的平均成绩较高,
∴乙会被公司录取.
【点评】此题主要考查了加权平均数的求法,要熟练掌握,解答此题的关键是:笔试占总成绩的20%、面试占30%、实习成绩占50%.
20.(2016 青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
【分析】(1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析.
【解答】解:(1)甲的平均成绩a==7(环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
其方差c=×[(3﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+3×(8﹣7)2+(9﹣7)2+(10﹣7)2]
=×(16+9+1+3+4+9)
=4.2(环);
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
【点评】本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用.熟练掌握平均数的计算,理解方差的概念,能够根据计算的数据进行综合分析.
测
试
卷
一.选择题(共10小题)
1.(2016 桂林)一组数据7,8,10,12,13的平均数是( )
A.7
B.9
C.10
D.12
2.(2016 呼伦贝尔)从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A.
B.
C.
D.
3.(2016 宁阳县模拟)下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
4.(2016 冷水江市校级模拟)某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.﹣3.5
B.3
C.0.5
D.﹣3
5.(2016 临沂)某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
A.4
B.3
C.2
D.1
6.(2016 南宁)某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分
B.82分
C.84分
D.86分
7.(2016 柘城县一模)九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
A.1:2
B.2:1
C.2:3
D.3:2
8.(2016 曲靖)某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
A.极差是6
B.众数是10
C.平均数是9.5
D.方差是16
9.(2016 株洲)甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
队员
平均成绩
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34
A.甲
B.乙
C.丙
D.丁
10.(2016 湖北襄阳)一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2
二.填空题(共4小题)
11.(2016 东营)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是______.
12.(2016 金华)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是______mg/L.
13.(2016 大连)下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是______岁.
14.(2016 大庆)甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是______(填“甲”或“乙”).
三.解答题(共6小题)
15.(2014秋 曹县期末)设一组数据x1,x2,…,xn的平均数为m,求下列各组数据的平均数:
(1)x1+3,x2+3,…,xn+3;
(2)2x1,2x2,…,2xn.
16.(2013秋 莘县期中)某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期
一
二
三
四
五
六
日
增减/辆
8
5
﹣2
﹣7
﹣6
10
13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
17.(2016 柳州)在一次“社会主义核心价值观”知识竞赛中,四个小组回答正确题数情况如图,求这四个小组回答正确题数的平均数.
18.(2016 新抚区模拟)为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的
信息解答下列问题:
(1)本次抽样测试的学生人数是______;
(2)扇形图中∠α的度数是______,并把条形统计图补充完整;
(3)对A,B,C,D四个等级依次赋分为90,75,65,55(单位:分),该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有______人;该市九年级学生体育平均成绩约为______分.
19.(2016春 商水县期末)一家公司打算招聘一名部门经理,现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价,笔试占总成绩的20%、面试占30%、实习成绩占50%,各项成绩如表所示.试判断谁会被公司录取,为什么?
应聘者
笔试
面试
实习
甲
85
83
90
乙
80
85
92
20.(2016 青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
参考答案与试题解析
一.选择题(共10小题)
1.(2016 桂林)一组数据7,8,10,12,13的平均数是( )
A.7
B.9
C.10
D.12
【分析】根据平均数的定义:平均数是指在一组数据中所有数据之和再除以数据的个数进行计算即可.
【解答】解:(7+8+10+12+13)÷5
=50÷5
=10
答:一组数据7,8,10,12,13的平均数是10.
故选:C.
【点评】本题考查了平均数的知识,掌握一组数据平均数的求解方法是解题关键.
2.(2016 呼伦贝尔)从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A.
B.
C.
D.
【分析】根据平均数的公式,求解即可.用所有数据的和除以(a+b+c).
【解答】解:由题意知,a个x1的和为ax1,b个x2的和为bx2,c个x3的和为cx3,数据总共有a+b+c个,
∴这个样本的平均数=,
故选:B.
【点评】本题考查了加权平均数的概念.平均数等于所有数据的和除以数据的个数.
3.(2016 宁阳县模拟)下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
【分析】运用平均数,中位数,众数的概念采用排除法即可解.
【解答】解:A、数据3,4,4,7,3的众数是4和3.故错误;
B、数据0,1,2,5,a的中位数因a的大小不确定,故中位数也无法确定.故错误;
C、一组数据的众数和中位数会出现相等的情况.故错误;
D、数据0,5,﹣7,﹣5,7的中位数和平数数都是0.对.
故选D.
【点评】本题重点考查平均数,中位数,众数的概念及求法.
4.(2016 冷水江市校级模拟)某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.﹣3.5
B.3
C.0.5
D.﹣3
【分析】根据题意可以得到求出的平均数与实际平均数之间的差值,本题得以解决.
【解答】解:∵(105﹣15)÷30=90÷30=3,
∴求出的平均数与实际平均数的差是﹣3,
故选D.
【点评】本题考查算术平均数,解题的关键是明确算术平均数的计算方法.
5.(2016 临沂)某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
A.4
B.3
C.2
D.1
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.本题利用加权平均数的公式即可求解.
【解答】解:根据题意得:
(1×1+2×2+4×3+2×4+1×5)÷10=3(小时),
答:这10名学生周末学均时间是3小时;
故选B.
【点评】此题考查了加权平均数,本题易出现的错误是求1,2,4,2,1这五个数的平均数,对平均数的理解不正确.
6.(2016 南宁)某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分
B.82分
C.84分
D.86分
【分析】利用加权平均数的公式直接计算即可得出答案.
【解答】解:
由加权平均数的公式可知===86,
故选D.
【点评】本题主要考查加权平均数的计算,掌握加权平均数的公式=是解题的关键.
7.(2016 柘城县一模)九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
A.1:2
B.2:1
C.2:3
D.3:2
【分析】设男生是x人,女生是y人,然后根据加权平均数公式列方程求解.
【解答】解:设男生是x人,女生是y人,
根据题意得:=80,
则82x+77y=80x+80y,即2x=3y,
则x:y=3:2.
故选D.
【点评】本题考查了加权平均数公式,数据的权能够反映数据的相对“重要程度”,要突出某个数据,只需要给它较大的“权”,权的差异对结果会产生直接的影响.(4)对于一组不同权重的数据,加权平均数更能反映数据的真实信息,理解公式是关键.
8.(2016 曲靖)某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
A.极差是6
B.众数是10
C.平均数是9.5
D.方差是16
【分析】极差是指一组数据中最大数据与最小数据的差;一组数据中出现次数最多的数据叫做众数;平均数是指在一组数据中所有数据之和再除以数据的个数;一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.
【解答】解:(A)极差为11﹣6=5,故(A)错误;
(B)根据出现次数最多的数据是10可得,众数是10,故(B)正确;
(C)平均数为(10+6+9+11+8+10)÷6=9,故(C)错误;
(D)方差为[(10﹣9)2+(6﹣9)2+(9﹣9)2+(11﹣9)2+(8﹣9)2+(10﹣9)2]=,故(D)错误.
故选(B)
【点评】本题主要考查了极差、众数、平均数以及方差的计算,注意:极差只能反映数据的波动范围,众数反映了一组数据的集中程度,平均数是反映数据集中趋势的一项指标,方差是反映一组数据的波动大小的一个量.
9.(2016 株洲)甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
队员
平均成绩
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34
A.甲
B.乙
C.丙
D.丁
【分析】首先比较平均数,然后比较方差,方差越小,越稳定.
【解答】解:∵==9.7,S2甲>S2乙,
∴选择丙.
故选C.
【点评】此题考查了方差的知识.注意方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
10.(2016 湖北襄阳)一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2
【分析】先根据平均数的定义求出x的值,再根据众数、中位数的定义和方差公式分别进行解答即可.
【解答】解:根据题意,=3,解得:x=3,
∴这组数据从小到大排列为:2,3,3,3,4;
则这组数据的中位数为3,
这组数据3出现的次数最多,出现了3次,故众数为3;
其方差是:×[(2﹣3)2+3×(3﹣3)2+(4﹣3)2]=0.4,
故选A.
【点评】本题考查了众数、中位数和方差,众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
二.填空题(共4小题)
11.(2016 东营)某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是 101 .
【分析】根据算术平均数的计算公式列式计算即可得解.
【解答】解:=(102+115+100+105+92+105+85+104)=×808=101.
故答案为:101.
【点评】本题考查了算术平均数,是基础题,准确计算是解题的关键.
12.(2016 金华)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是 1 mg/L.
【分析】根据题意可以求得这6次总的含量,由折线统计图可以得到除第3次的含量,从而可以得到第3次检测得到的氨氮含量.
【解答】解:由题意可得,
第3次检测得到的氨氮含量是:1.5×6﹣(1.6+2+1.5+1.4+1.5)=9﹣8=1mg/L,
故答案为:1.
【点评】本题考查算术平均数、折线统计图,解题的关键是明确题意,找出所求问题需要的条件.
13.(2016 大连)下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是 15 岁.
【分析】根据加权平均数的计算公式列出算式,再进行计算即可.
【解答】解:根据题意得:
(13×1+14×1+15×7+16×3)÷12=15(岁),
即该校女子排球队队员的平均年龄为15岁.
故答案为:15.
【点评】此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键.
14.(2016 大庆)甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是 甲 (填“甲”或“乙”).
【分析】计算出乙的平均数和方差后,与甲的方差比较后,可以得出判断.
【解答】解:乙组数据的平均数=(0+1+5+9+10)÷5=5,
乙组数据的方差S2=[(0﹣5)2+(1﹣5)2+(9﹣5)2+(10﹣5)2]=16.4,
∵S2甲<S2乙,
∴成绩较为稳定的是甲.
故答案为:甲.
【点评】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
三.解答题(共6小题)
15.(2014秋 曹县期末)设一组数据x1,x2,…,xn的平均数为m,求下列各组数据的平均数:
(1)x1+3,x2+3,…,xn+3;
(2)2x1,2x2,…,2xn.
【分析】首先根据求平均数的公式:=,得出x1+x2+…+xn,再利用此公式求出(1)x1+3,x2+3,…,xn+3以及(2)2x1,2x2,…,2xn的平均数.
【解答】解:设一组数据x1,x2,…,xn的平均数是m,
即=,
则x1+x2+…+xn=mn.
(1)∵x1+x2+…+xn=mn,
∴x1+3+x2+3+…+xn+3=mn+3n,
∴x1+3,x2+3,…,xn+3的平均数是=m+3;
(2)∵x1+x2+…+xn=mn,
∴2x1+2x2+…+2xn=2mn,
∴2x1,2x2,…,2xn的平均数是=2m.
【点评】本题考查的是样本平均数的求法及运用,熟记平均数公式是解题的关键.
16.(2013秋 莘县期中)某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期
一
二
三
四
五
六
日
增减/辆
8
5
﹣2
﹣7
﹣6
10
13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
【分析】(1)读统计图,直接回答;
(2)根据平均数的概念计算.
【解答】解:(1)从统计表格中得出星期四经过红绿灯路口的小汽车最少,为93辆;星期日经过红绿灯路口的小汽车最多,为113辆;
(2)平均数=(8+5﹣2﹣7﹣6+10+13)÷7+100=103,
故平均每天有103辆小汽车通过这个红绿灯路口.
答:(1)星期四最少,为93辆;星期日最多,为113辆;
(2)平均每天有103辆小汽车通过这个红绿灯路口.
【点评】本题考查了从统计表格得出信息的能力和计算平均数的能力.
17.(2016 柳州)在一次“社会主义核心价值观”知识竞赛中,四个小组回答正确题数情况如图,求这四个小组回答正确题数的平均数.
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.
【解答】解:(6+12+16+10)÷4
=44÷4
=11
∴这四个小组回答正确题数的平均数是11.
【点评】此题主要考查了平均数的含义和求法,以及条形统计图的应用,要熟练掌握.
18.(2016 新抚区模拟)为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的
信息解答下列问题:
(1)本次抽样测试的学生人数是 400 ;
(2)扇形图中∠α的度数是 108° ,并把条形统计图补充完整;
(3)对A,B,C,D四个等级依次赋分为90,75,65,55(单位:分),该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有 900 人;该市九年级学生体育平均成绩约为 75.5 分.
【分析】(1)根据B级的人数和百分比求出学生人数;
(2)求出A级的百分比,360°乘百分比即为∠α的度数,根据各等级人数之和等于总人数求出C等级人数,补全条形图;
(3)根据样本中D等级所占比例乘以总人数9000可得,运用加权平均数的求法即可求出九年级学生体育平均成绩.
【解答】解:(1)本次抽样测试的学生人数是:160÷40%=400,
故答案为:400;
(2)扇形图中∠α的度数是:×360°=108°,
C等级人数为:400﹣120﹣160﹣40=80(人),补全条形图如图:
故答案为:108°;
(3)测试等级为D的约有×9000=900(人),
学生体育平均成绩约为:90×+75×+65×+55×=75.5(分),
故答案为:900,75.5.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,扇形统计图直接反映部分占总体的百分比大小.
19.(2016春 商水县期末)一家公司打算招聘一名部门经理,现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价,笔试占总成绩的20%、面试占30%、实习成绩占50%,各项成绩如表所示.试判断谁会被公司录取,为什么?
应聘者
笔试
面试
实习
甲
85
83
90
乙
80
85
92
【分析】首先根据加权平均数的计算方法,分别求出甲、乙的平均成绩各是多少;然后比较大小,判断出谁会被公司录取即可.
【解答】解:甲的平均成绩为:
85×20%+83×30%+90×50%
=17+24.9+45
=86.9
乙的平均成绩为:
80×20%+85×30%+92×50%
=16+25.5+46
=87.5
∵87.5>86.9,
∴乙的平均成绩较高,
∴乙会被公司录取.
【点评】此题主要考查了加权平均数的求法,要熟练掌握,解答此题的关键是:笔试占总成绩的20%、面试占30%、实习成绩占50%.
20.(2016 青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
【分析】(1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析.
【解答】解:(1)甲的平均成绩a==7(环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
其方差c=×[(3﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+3×(8﹣7)2+(9﹣7)2+(10﹣7)2]
=×(16+9+1+3+4+9)
=4.2(环);
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
【点评】本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用.熟练掌握平均数的计算,理解方差的概念,能够根据计算的数据进行综合分析.
