24.2.1点与圆的位置关系以及圆的有关概念 同步练习测试卷(含答案解析)
文档属性
| 名称 | 24.2.1点与圆的位置关系以及圆的有关概念 同步练习测试卷(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 20:14:58 | ||
图片预览



文档简介
沪科版九年级数学下册24.2.1
《点与圆的位置关系以及圆的有关概念》测试卷
一.选择题(共10小题)
1.(2017 德州校级自主招生)⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
2.(2016 陕西校级模拟)⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
3.(2016 路北区三模)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
A.3
B.4
C.5
D.6
4.(2016 松江区三模)如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.不能确定
5.(2016春 盐都区月考)圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
6.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
7.(2016春 保亭县期中)一条排水管的截面如图所示,已知排水管的截面圆半径是10cm,截面圆圆心O到水面AB的距离是6cm,则水面宽是( )
A.6
B.8
C.10
D.16
8.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
9.(2015 贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
10.(2015秋 江宁区期末)如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M
B.点N
C.点P
D.点Q
二.填空题(共4小题)
11.(2016 德州校级自主招生)圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O______.
12.(2016 闵行区一模)在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为______.
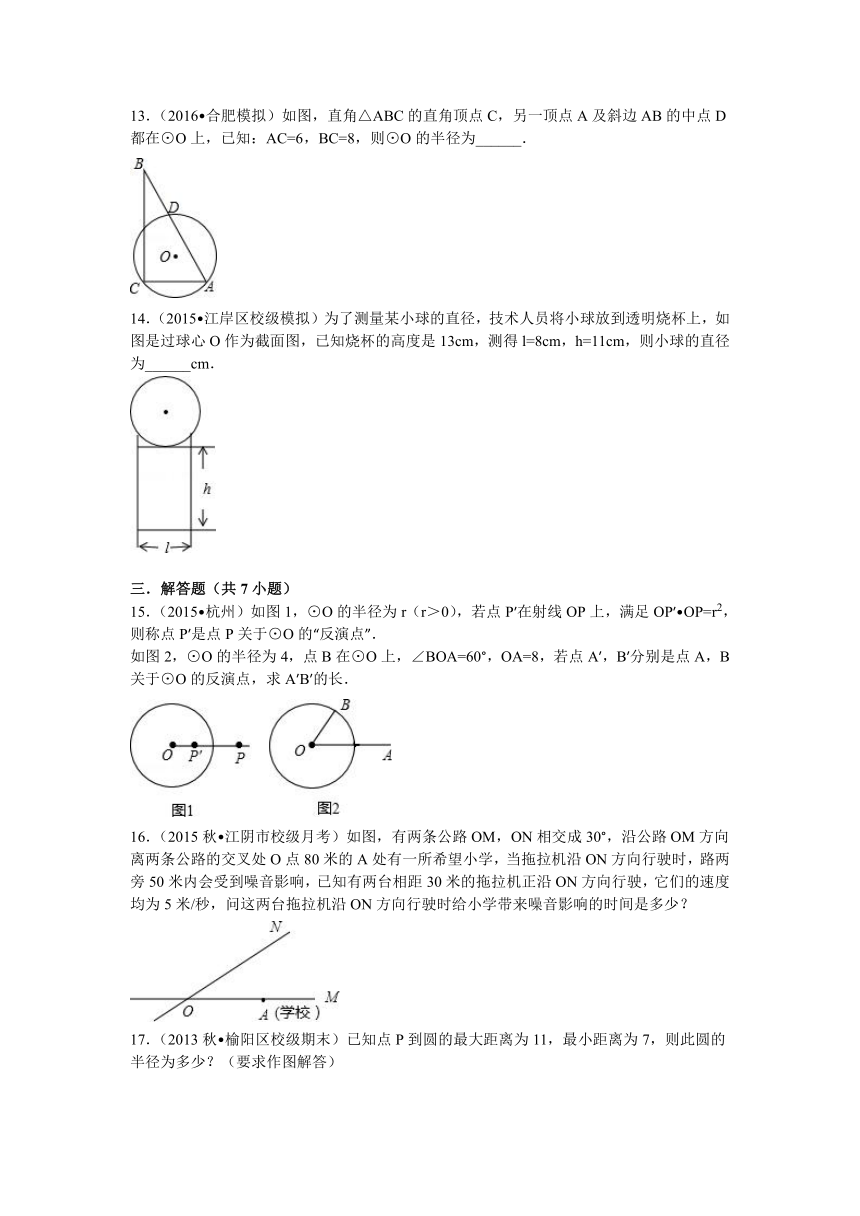
13.(2016 合肥模拟)如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为______.
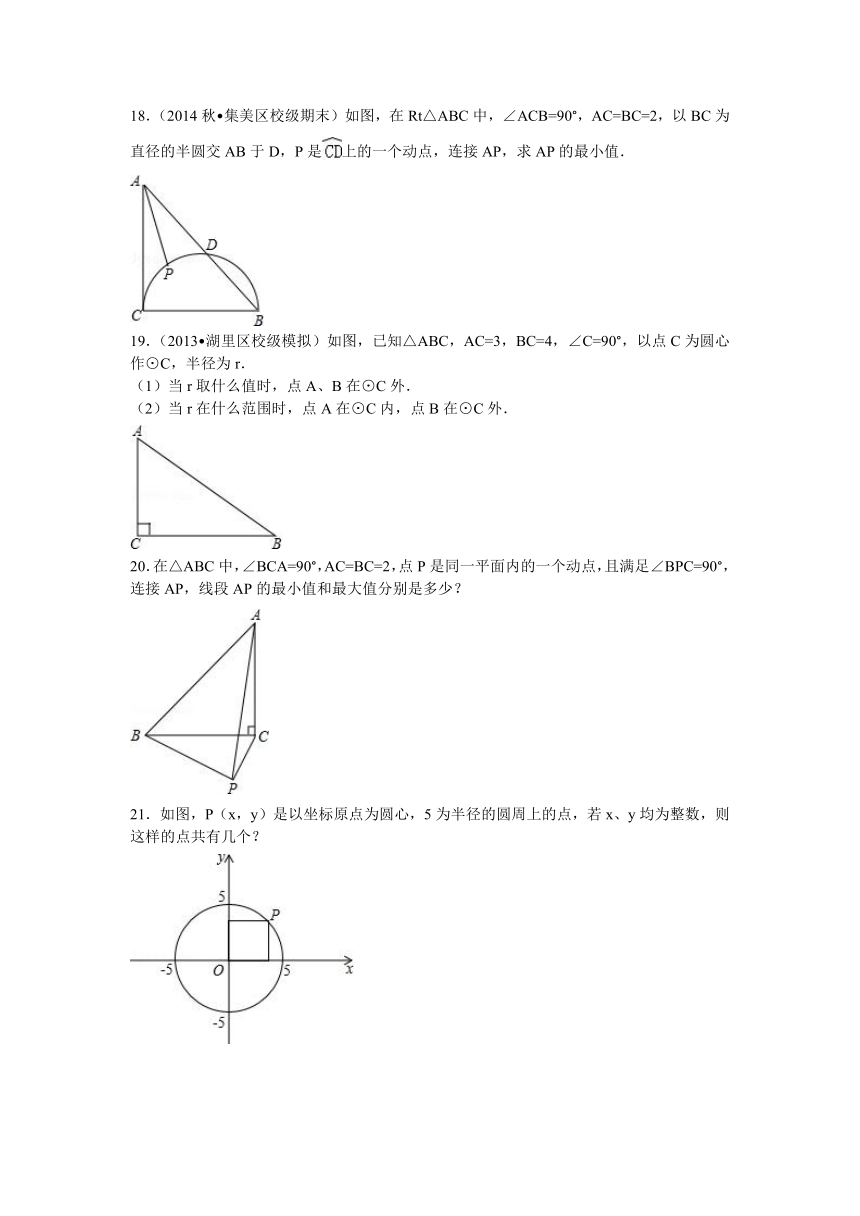
14.(2015 江岸区校级模拟)为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为______cm.
三.解答题(共7小题)
15.(2015 杭州)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
16.(2015秋 江阴市校级月考)如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
17.(2013秋 榆阳区校级期末)已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
18.(2014秋 集美区校级期末)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
19.(2013 湖里区校级模拟)如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
20.在△ABC中,∠BCA=90°,AC=BC=2,点P是同一平面内的一个动点,且满足∠BPC=90°,连接AP,线段AP的最小值和最大值分别是多少?
21.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y均为整数,则这样的点共有几个?
参考答案与试题解析
一.选择题(共10小题)
1.(2017 德州校级自主招生)⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
【分析】由条件计算出OP的长度与半径比较大小即可.
【解答】解:由题意可知△OPM为直角三角形,且PM=3,OM=4,
由勾股定理可求得OP=5=r,
故点P在⊙O上,
故选B.
【点评】本题主要考查点和圆的位置关系的判定,只要计算出P点到圆心的距离再与半径比较大小即可.
2.(2016 陕西校级模拟)⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
【分析】根据点到圆心的距离与圆的半径之间的关系:“点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”来求解.
【解答】解:∵圆心O的坐标为(0,0),点P的坐标为(4,2),
∴OP==<5,因而点P在⊙O内.
故选A.
【点评】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.
3.(2016 路北区三模)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
A.3
B.4
C.5
D.6
【分析】根据点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,可得答案.
【解答】解:由勾股定理,得BD==5.
在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,得
3<r<5,
故选:B.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
4.(2016 松江区三模)如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.不能确定
【分析】连接OA,过点O作OD⊥AB,并作点O关于AB的对称点O′,设⊙O的半径为R,则OD=,可得OO′,利用圆和直线的位置关系可得结论.
【解答】解:连接OA,过点O作OD⊥AB,并作点O关于AB的对称点O′,设⊙O的半径为R,
∵OD⊥AB,△ABC为正三角形,
则OD=AO sin30°=R,
∴OO′=R,
∴圆心O关于直线AB的对称点O′和⊙O的位置关系是在圆上,
故选B.
【点评】本题主要考查了圆和直线的位置关系,掌握点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r;②点P在圆上 d=r;①点P在圆内 d<r是解答此题的关键
5.(2016春 盐都区月考)圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
【分析】求得各点到圆心的距离,然后利用距离与半径的大小关系即可判断.
【解答】解:A、d=5<r,所以在圆内;
B、d=4<r,所以在圆内;
C、d=<r,所以在圆内;
D、d=2>r,所以在圆外.
故选D.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
6.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
【分析】由垂径定理,可得AD=AB,然后由勾股定理求得OD的长,继而求得中间柱CD的高度.
【解答】解:∵CD是中间柱,
即=,
∴OC⊥AB,
∴AD=BD=AB=×16=8(m),
∵半径OA=10m,
在Rt△AOD中,OD==6(m),
∴CD=OC﹣OD=10﹣6=4(m).
故选B.
【点评】此题考查了垂径定理的应用与勾股定理.此题比较简单,注意数形结合思想的应用.
7.(2016春 保亭县期中)一条排水管的截面如图所示,已知排水管的截面圆半径是10cm,截面圆圆心O到水面AB的距离是6cm,则水面宽是( )
A.6
B.8
C.10
D.16
【分析】先根据垂径定理得出AB=2BC,再根据勾股定理求出BC的长,进而可得出答案.
【解答】解:∵截面圆圆心O到水面的距离OC是6,
∴OC⊥AB,
∴AB=2BC,
在Rt△BOC中,OB=10,OC=6,
∴BC===8,
∴AB=2BC=2×8=16.
故选D.
【点评】本题考查的是垂径定理的应用,熟知垂径定理及勾股定理是解答此题的关键.
8.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
【分析】连接OA,过点O作OD⊥AB于点D,由垂径定理可知,AD=AB=(9﹣1)=4,设OA=r,则OD=r﹣3,在Rt△OAD中利用勾股定理求出r的值即可.
【解答】解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=AB=(9﹣1)=4cm,
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=cm.
故选:C.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
9.(2015 贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
【分析】取OP的中点N,连结MN,OQ,如图可判断MN为△POQ的中位线,则MN=OQ=1,则点M在以N为圆心,1为半径的圆上,当点M在ON上时,OM最小,最小值为1.
【解答】解:设OP与⊙O交于点N,连结MN,OQ,如图,
∵OP=4,ON=2,
∴N是OP的中点,
∵M为PQ的中点,
∴MN为△POQ的中位线,
∴MN=OQ=×2=1,
∴点M在以N为圆心,1为半径的圆上,
当点M在ON上时,OM最小,最小值为1,
∴线段OM的最小值为1.
故选B.
【点评】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
10.(2015秋 江宁区期末)如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M
B.点N
C.点P
D.点Q
【分析】连接OM,ON,OQ,OP,由线段垂直平分线的性质可得出OM=ON=OQ,据此可得出结论.
【解答】解:连接OM,ON,OQ,OP,
∵MN、MQ的垂直平分线交于点O,
∴OM=ON=OQ,
∴M、N、Q再以点O为圆心的圆上,OP与ON的大小不能确定,
∴点P不一定在圆上.
故选C.
【点评】本题考查的是点与圆的位置关系及线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.
二.填空题(共4小题)
11.(2016 德州校级自主招生)圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O 上 .
【分析】先由勾股定理求得点P到圆心O的距离,再根据点P与圆心的距离与半径的大小关系,来判断出点P与⊙O的位置关系.
【解答】解:∵点P的坐标为(﹣3,4),
∴由勾股定理得,点P到圆心O的距离==5,
∴点P在⊙O上.
故答案为上.
【点评】本题考查了勾股定理,点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r;②点P在圆上 d=r;③点P在圆内 d<r.
12.(2016 闵行区一模)在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为 12<r<13 .
【分析】熟记“设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”即可求解,
【解答】解:如果以点A为圆心作圆,使点C在圆A内,则r>12,
点B在圆A外,则r<13,
因而圆A半径r的取值范围为12<r<13.
故答案为12<r<13.
【点评】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.
13.(2016 合肥模拟)如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为 .
【分析】如图连接CD、OD、OC,延长DO交AC于E,设半径为R,先证明DE⊥AC,DE=CB,在RT△OCE中,利用勾股定理即可解决问题.
【解答】解:如图连接CD、OD、OC,延长DO交AC于E,设半径为R.
在RT△ABC中,∵∠ACB=90°,BC=8,AC=6,
∴AB===10,
∵BD=AD=5,
∴CD=AD=5,
∵DC=DA,
=,
∴DO⊥AC,EC=AE=3,
∴ED∥BC,∵BD=AD,
∴EC=EA,
∴DE=BC=4,
在RT△COE中,∵∠OEC=90°,
∴CO2=OE2+CE2,
∴R2=(4﹣R)2+32,
∴R=.
【点评】本题考查点与圆的位置关系,三角形的中位线的性质,垂径定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
14.(2015 江岸区校级模拟)为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为 10 cm.
【分析】连接AB,过点O作OD⊥AB于点D,根据垂径定理求出BD的长,设小球的半径为r,在Rt△DOB中根据勾股定理求出r的值,进而可得出结论.
【解答】解:如图所示,连接AB,过点O作OD⊥AB于点D,设OB=r,
∵l=8cm,h=11cm,
∴BD=×8=4cm.
∵烧杯的高度是13cm,
∴OD=r﹣(13﹣11)=r﹣2,
∴OB2=OD2+BD2,即r2=(r﹣2)2+42,解得r=5cm,
∴小球的直径为10cm.
故答案为:10.
【点评】本题考查的是垂径定理,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.
三.解答题(共7小题)
15.(2015 杭州)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
【分析】设OA交⊙O于C,连结B′C,如图2,根据新定义计算出OA′=2,OB′=4,则点A′为OC的中点,点B和B′重合,再证明△OBC为等边三角形,则B′A′⊥OC,然后在Rt△OA′B′中,利用正弦的定义可求A′B′的长.
【解答】解:设OA交⊙O于C,连结B′C,如图2,
∵OA′ OA=42,
而r=4,OA=8,
∴OA′=2,
∵OB′ OB=42,
∴OB′=4,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′=,
∴A′B′=4sin60°=2.
【点评】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了阅读理解能力.
16.(2015秋 江阴市校级月考)如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
【分析】过点A作AC⊥ON,求出AC的长,第一台到B点时开始对学校有噪音影响,第一台到C点时,第二台到B点也开始有影响,第一台到D点,第二台到C点,直到第二台到D点噪音才消失.
【解答】解:如图,
过点A作AC⊥ON,
∵∠MON=30°,OA=80米,
∴AC=40米,
当第一台拖拉机到B点时对学校产生噪音影响,此时AB=50,
由勾股定理得:BC=30,
第一台拖拉机到D点时噪音消失,
所以CD=30.
由于两台拖拉机相距30米,则第一台到D点时第二台在C点,还须前行30米后才对学校没有噪音影响.
所以影响时间应是:90÷5=18秒.
答:这两台拖拉机沿ON方向行驶给小学带来噪音影响的时间是18秒.
【点评】本题考查的是点与圆的位置关系,根据拖拉机行驶的方向,速度,以及它在以A为圆心,50米为半径的圆内行驶的BD的弦长,求出对小学产生噪音的时间.
17.(2013秋 榆阳区校级期末)已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9.
【点评】本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.
18.(2014秋 集美区校级期末)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
【分析】找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可.
【解答】解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE==,P2E=1,
∴AP2=﹣1.
【点评】本题考查了勾股定理、最短路径问题,利用两点之间线段最短是解题的关键.
19.(2013 湖里区校级模拟)如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
【分析】(1)要保证点在圆外,则点到圆心的距离应大于圆的半径,根据这一数量关系就可得到r的取值范围;
(2)根据点到圆心的距离小于圆的半径,则点在圆内和点到圆心的距离应大于圆的半径,则点在圆外求得r的取值范围.
【解答】解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
【点评】能够根据点和圆的位置关系得到相关的数量关系.
20.在△ABC中,∠BCA=90°,AC=BC=2,点P是同一平面内的一个动点,且满足∠BPC=90°,连接AP,线段AP的最小值和最大值分别是多少?
【分析】由于∠BPC=90°,所以点P在以BC为直径的圆O上.以BC为直径作圆O,连结AO交圆于两点,则AP1最小,AP2最大.
【解答】解:如图,以BC为直径作圆O,连结AO交圆于两点P1,P2,则AP1最小,AP2最大.
∵AP1 AP2=AC2,AC=2,P1P2=2,
∴AP1(AP1+2)=4,
解得AP1=﹣1±(负值舍去),
∴AP2=﹣1++2=1+.
故线段AP的最小值和最大值分别是﹣1+和1+.
【点评】本题考查了圆周角定理,点与圆的位置关系,等腰直角三角形的性质,切割线定理,有一定难度.确定P点位置是解题的关键.
21.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y均为整数,则这样的点共有几个?
【分析】因为P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,根据题意,x2+y2=25,若x、y都是整数,其实质就是求方程的整数解.
【解答】解:∵P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,
即圆周上的任意一点到原点的距离为5,
由题意得:=5,即x2+y2=25,
又∵x、y都是整数,
∴方程的整数解分别是:x=0,y=5;x=3,y=4;x=4,y=3;
x=5,y=0;x=﹣3,y=4;x=﹣4,y=3;
x=﹣5,y=0;x=﹣3,y=﹣4;x=﹣4,y=﹣3;
x=0,y=﹣5;x=3,y=﹣4;x=4,y=﹣3.
共12对,所以点的坐标有12个.
分别是:(0,5);(3,4);(4,3);(5,0);(﹣3,4);(﹣4,3);(﹣5,0);(﹣3,﹣4);(﹣4,﹣3);(0,﹣5);(3,﹣4);(4,﹣3).
【点评】本题考查了点和圆的位置关系以及坐标与图形的性质,结合圆和直角三角形的知识,考查了二元二次方程的整数解和点的坐标问题.
《点与圆的位置关系以及圆的有关概念》测试卷
一.选择题(共10小题)
1.(2017 德州校级自主招生)⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
2.(2016 陕西校级模拟)⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
3.(2016 路北区三模)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
A.3
B.4
C.5
D.6
4.(2016 松江区三模)如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.不能确定
5.(2016春 盐都区月考)圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
6.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
7.(2016春 保亭县期中)一条排水管的截面如图所示,已知排水管的截面圆半径是10cm,截面圆圆心O到水面AB的距离是6cm,则水面宽是( )
A.6
B.8
C.10
D.16
8.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
9.(2015 贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
10.(2015秋 江宁区期末)如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M
B.点N
C.点P
D.点Q
二.填空题(共4小题)
11.(2016 德州校级自主招生)圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O______.
12.(2016 闵行区一模)在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为______.
13.(2016 合肥模拟)如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为______.
14.(2015 江岸区校级模拟)为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为______cm.
三.解答题(共7小题)
15.(2015 杭州)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
16.(2015秋 江阴市校级月考)如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
17.(2013秋 榆阳区校级期末)已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
18.(2014秋 集美区校级期末)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
19.(2013 湖里区校级模拟)如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
20.在△ABC中,∠BCA=90°,AC=BC=2,点P是同一平面内的一个动点,且满足∠BPC=90°,连接AP,线段AP的最小值和最大值分别是多少?
21.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y均为整数,则这样的点共有几个?
参考答案与试题解析
一.选择题(共10小题)
1.(2017 德州校级自主招生)⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
【分析】由条件计算出OP的长度与半径比较大小即可.
【解答】解:由题意可知△OPM为直角三角形,且PM=3,OM=4,
由勾股定理可求得OP=5=r,
故点P在⊙O上,
故选B.
【点评】本题主要考查点和圆的位置关系的判定,只要计算出P点到圆心的距离再与半径比较大小即可.
2.(2016 陕西校级模拟)⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
【分析】根据点到圆心的距离与圆的半径之间的关系:“点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”来求解.
【解答】解:∵圆心O的坐标为(0,0),点P的坐标为(4,2),
∴OP==<5,因而点P在⊙O内.
故选A.
【点评】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.
3.(2016 路北区三模)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
A.3
B.4
C.5
D.6
【分析】根据点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,可得答案.
【解答】解:由勾股定理,得BD==5.
在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,得
3<r<5,
故选:B.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
4.(2016 松江区三模)如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.不能确定
【分析】连接OA,过点O作OD⊥AB,并作点O关于AB的对称点O′,设⊙O的半径为R,则OD=,可得OO′,利用圆和直线的位置关系可得结论.
【解答】解:连接OA,过点O作OD⊥AB,并作点O关于AB的对称点O′,设⊙O的半径为R,
∵OD⊥AB,△ABC为正三角形,
则OD=AO sin30°=R,
∴OO′=R,
∴圆心O关于直线AB的对称点O′和⊙O的位置关系是在圆上,
故选B.
【点评】本题主要考查了圆和直线的位置关系,掌握点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r;②点P在圆上 d=r;①点P在圆内 d<r是解答此题的关键
5.(2016春 盐都区月考)圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
A.(3,4)
B.(4,4)
C.(4,5)
D.(4,6)
【分析】求得各点到圆心的距离,然后利用距离与半径的大小关系即可判断.
【解答】解:A、d=5<r,所以在圆内;
B、d=4<r,所以在圆内;
C、d=<r,所以在圆内;
D、d=2>r,所以在圆外.
故选D.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
6.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
【分析】由垂径定理,可得AD=AB,然后由勾股定理求得OD的长,继而求得中间柱CD的高度.
【解答】解:∵CD是中间柱,
即=,
∴OC⊥AB,
∴AD=BD=AB=×16=8(m),
∵半径OA=10m,
在Rt△AOD中,OD==6(m),
∴CD=OC﹣OD=10﹣6=4(m).
故选B.
【点评】此题考查了垂径定理的应用与勾股定理.此题比较简单,注意数形结合思想的应用.
7.(2016春 保亭县期中)一条排水管的截面如图所示,已知排水管的截面圆半径是10cm,截面圆圆心O到水面AB的距离是6cm,则水面宽是( )
A.6
B.8
C.10
D.16
【分析】先根据垂径定理得出AB=2BC,再根据勾股定理求出BC的长,进而可得出答案.
【解答】解:∵截面圆圆心O到水面的距离OC是6,
∴OC⊥AB,
∴AB=2BC,
在Rt△BOC中,OB=10,OC=6,
∴BC===8,
∴AB=2BC=2×8=16.
故选D.
【点评】本题考查的是垂径定理的应用,熟知垂径定理及勾股定理是解答此题的关键.
8.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
【分析】连接OA,过点O作OD⊥AB于点D,由垂径定理可知,AD=AB=(9﹣1)=4,设OA=r,则OD=r﹣3,在Rt△OAD中利用勾股定理求出r的值即可.
【解答】解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=AB=(9﹣1)=4cm,
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=cm.
故选:C.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
9.(2015 贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
【分析】取OP的中点N,连结MN,OQ,如图可判断MN为△POQ的中位线,则MN=OQ=1,则点M在以N为圆心,1为半径的圆上,当点M在ON上时,OM最小,最小值为1.
【解答】解:设OP与⊙O交于点N,连结MN,OQ,如图,
∵OP=4,ON=2,
∴N是OP的中点,
∵M为PQ的中点,
∴MN为△POQ的中位线,
∴MN=OQ=×2=1,
∴点M在以N为圆心,1为半径的圆上,
当点M在ON上时,OM最小,最小值为1,
∴线段OM的最小值为1.
故选B.
【点评】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
10.(2015秋 江宁区期末)如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M
B.点N
C.点P
D.点Q
【分析】连接OM,ON,OQ,OP,由线段垂直平分线的性质可得出OM=ON=OQ,据此可得出结论.
【解答】解:连接OM,ON,OQ,OP,
∵MN、MQ的垂直平分线交于点O,
∴OM=ON=OQ,
∴M、N、Q再以点O为圆心的圆上,OP与ON的大小不能确定,
∴点P不一定在圆上.
故选C.
【点评】本题考查的是点与圆的位置关系及线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.
二.填空题(共4小题)
11.(2016 德州校级自主招生)圆心在原点O,半径为5的⊙O,则点P(﹣3,4)在⊙O 上 .
【分析】先由勾股定理求得点P到圆心O的距离,再根据点P与圆心的距离与半径的大小关系,来判断出点P与⊙O的位置关系.
【解答】解:∵点P的坐标为(﹣3,4),
∴由勾股定理得,点P到圆心O的距离==5,
∴点P在⊙O上.
故答案为上.
【点评】本题考查了勾股定理,点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r;②点P在圆上 d=r;③点P在圆内 d<r.
12.(2016 闵行区一模)在Rt△ABC中,∠C=90°,AC=12,BC=5,以点A为圆心作⊙A,要使B、C两点中的一点在圆外,另一点在圆内,那么⊙A的半径长r的取值范围为 12<r<13 .
【分析】熟记“设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”即可求解,
【解答】解:如果以点A为圆心作圆,使点C在圆A内,则r>12,
点B在圆A外,则r<13,
因而圆A半径r的取值范围为12<r<13.
故答案为12<r<13.
【点评】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.
13.(2016 合肥模拟)如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为 .
【分析】如图连接CD、OD、OC,延长DO交AC于E,设半径为R,先证明DE⊥AC,DE=CB,在RT△OCE中,利用勾股定理即可解决问题.
【解答】解:如图连接CD、OD、OC,延长DO交AC于E,设半径为R.
在RT△ABC中,∵∠ACB=90°,BC=8,AC=6,
∴AB===10,
∵BD=AD=5,
∴CD=AD=5,
∵DC=DA,
=,
∴DO⊥AC,EC=AE=3,
∴ED∥BC,∵BD=AD,
∴EC=EA,
∴DE=BC=4,
在RT△COE中,∵∠OEC=90°,
∴CO2=OE2+CE2,
∴R2=(4﹣R)2+32,
∴R=.
【点评】本题考查点与圆的位置关系,三角形的中位线的性质,垂径定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
14.(2015 江岸区校级模拟)为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为 10 cm.
【分析】连接AB,过点O作OD⊥AB于点D,根据垂径定理求出BD的长,设小球的半径为r,在Rt△DOB中根据勾股定理求出r的值,进而可得出结论.
【解答】解:如图所示,连接AB,过点O作OD⊥AB于点D,设OB=r,
∵l=8cm,h=11cm,
∴BD=×8=4cm.
∵烧杯的高度是13cm,
∴OD=r﹣(13﹣11)=r﹣2,
∴OB2=OD2+BD2,即r2=(r﹣2)2+42,解得r=5cm,
∴小球的直径为10cm.
故答案为:10.
【点评】本题考查的是垂径定理,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.
三.解答题(共7小题)
15.(2015 杭州)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
【分析】设OA交⊙O于C,连结B′C,如图2,根据新定义计算出OA′=2,OB′=4,则点A′为OC的中点,点B和B′重合,再证明△OBC为等边三角形,则B′A′⊥OC,然后在Rt△OA′B′中,利用正弦的定义可求A′B′的长.
【解答】解:设OA交⊙O于C,连结B′C,如图2,
∵OA′ OA=42,
而r=4,OA=8,
∴OA′=2,
∵OB′ OB=42,
∴OB′=4,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′=,
∴A′B′=4sin60°=2.
【点评】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了阅读理解能力.
16.(2015秋 江阴市校级月考)如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
【分析】过点A作AC⊥ON,求出AC的长,第一台到B点时开始对学校有噪音影响,第一台到C点时,第二台到B点也开始有影响,第一台到D点,第二台到C点,直到第二台到D点噪音才消失.
【解答】解:如图,
过点A作AC⊥ON,
∵∠MON=30°,OA=80米,
∴AC=40米,
当第一台拖拉机到B点时对学校产生噪音影响,此时AB=50,
由勾股定理得:BC=30,
第一台拖拉机到D点时噪音消失,
所以CD=30.
由于两台拖拉机相距30米,则第一台到D点时第二台在C点,还须前行30米后才对学校没有噪音影响.
所以影响时间应是:90÷5=18秒.
答:这两台拖拉机沿ON方向行驶给小学带来噪音影响的时间是18秒.
【点评】本题考查的是点与圆的位置关系,根据拖拉机行驶的方向,速度,以及它在以A为圆心,50米为半径的圆内行驶的BD的弦长,求出对小学产生噪音的时间.
17.(2013秋 榆阳区校级期末)已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9.
【点评】本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.
18.(2014秋 集美区校级期末)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
【分析】找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可.
【解答】解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE==,P2E=1,
∴AP2=﹣1.
【点评】本题考查了勾股定理、最短路径问题,利用两点之间线段最短是解题的关键.
19.(2013 湖里区校级模拟)如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
【分析】(1)要保证点在圆外,则点到圆心的距离应大于圆的半径,根据这一数量关系就可得到r的取值范围;
(2)根据点到圆心的距离小于圆的半径,则点在圆内和点到圆心的距离应大于圆的半径,则点在圆外求得r的取值范围.
【解答】解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
【点评】能够根据点和圆的位置关系得到相关的数量关系.
20.在△ABC中,∠BCA=90°,AC=BC=2,点P是同一平面内的一个动点,且满足∠BPC=90°,连接AP,线段AP的最小值和最大值分别是多少?
【分析】由于∠BPC=90°,所以点P在以BC为直径的圆O上.以BC为直径作圆O,连结AO交圆于两点,则AP1最小,AP2最大.
【解答】解:如图,以BC为直径作圆O,连结AO交圆于两点P1,P2,则AP1最小,AP2最大.
∵AP1 AP2=AC2,AC=2,P1P2=2,
∴AP1(AP1+2)=4,
解得AP1=﹣1±(负值舍去),
∴AP2=﹣1++2=1+.
故线段AP的最小值和最大值分别是﹣1+和1+.
【点评】本题考查了圆周角定理,点与圆的位置关系,等腰直角三角形的性质,切割线定理,有一定难度.确定P点位置是解题的关键.
21.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y均为整数,则这样的点共有几个?
【分析】因为P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,根据题意,x2+y2=25,若x、y都是整数,其实质就是求方程的整数解.
【解答】解:∵P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,
即圆周上的任意一点到原点的距离为5,
由题意得:=5,即x2+y2=25,
又∵x、y都是整数,
∴方程的整数解分别是:x=0,y=5;x=3,y=4;x=4,y=3;
x=5,y=0;x=﹣3,y=4;x=﹣4,y=3;
x=﹣5,y=0;x=﹣3,y=﹣4;x=﹣4,y=﹣3;
x=0,y=﹣5;x=3,y=﹣4;x=4,y=﹣3.
共12对,所以点的坐标有12个.
分别是:(0,5);(3,4);(4,3);(5,0);(﹣3,4);(﹣4,3);(﹣5,0);(﹣3,﹣4);(﹣4,﹣3);(0,﹣5);(3,﹣4);(4,﹣3).
【点评】本题考查了点和圆的位置关系以及坐标与图形的性质,结合圆和直角三角形的知识,考查了二元二次方程的整数解和点的坐标问题.
