24.2.2垂径定理 同步练习测试卷(含答案解析)
文档属性
| 名称 | 24.2.2垂径定理 同步练习测试卷(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 453.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-06 00:00:00 | ||
图片预览




文档简介
沪科版九年级数学下册24.2.2《垂径定理》测试卷
一.选择题(共10小题)
1.(2016 牡丹江)如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3
B.2.5
C.4
D.3.5
2.(2016 黄石)如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5
B.7
C.9
D.11
3.(2016 黔南州)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
A.cm
B.3cm
C.3cm
D.6cm
4.(2016 三明)如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A.2
B.3
C.4
D.5
5.(2016 安徽校级自主招生)如图,AB是⊙O的弦,C是AB的三等分点,连接OC并延长交⊙O于点D.若OC=3,CD=2,则圆心O到弦AB的距离是( )
A.6
B.9﹣
C.
D.25﹣3
6.(2016 桐城市模拟)一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )
A.0.5
B.1
C.2
D.4
7.(2016 新泰市二模)如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )
A.8cm
B.16cm
C.8cm
D.16cm
8.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
9.(2016 永康市模拟)如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为( )
A.m
B.2m
C.4m
D.6m
10.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
二.填空题(共4小题)
11.(2016 安顺)如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=______.
12.(2016 贵阳)如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是______.
13.(2016 海口校级一模)如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是______
cm.
14.(2015 六盘水)赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=______米.
三.解答题(共6小题)
15.(2016 西安校级三模)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
16.(2016 黄冈校级自主招生)如图,在⊙O中,弦CD垂直于直径AB.M是OC的中点,AM的延长线交⊙O于E,DE交BC于N.求证:BN=CN.
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
18.(2016 槐荫区二模)如图,已知⊙O的半径为15,弦AB=24,求点O到AB的距离及∠OAB的余弦值.
19.(2016 嘉定区一模)已知:如图,已知点A、B、C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=时.
(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
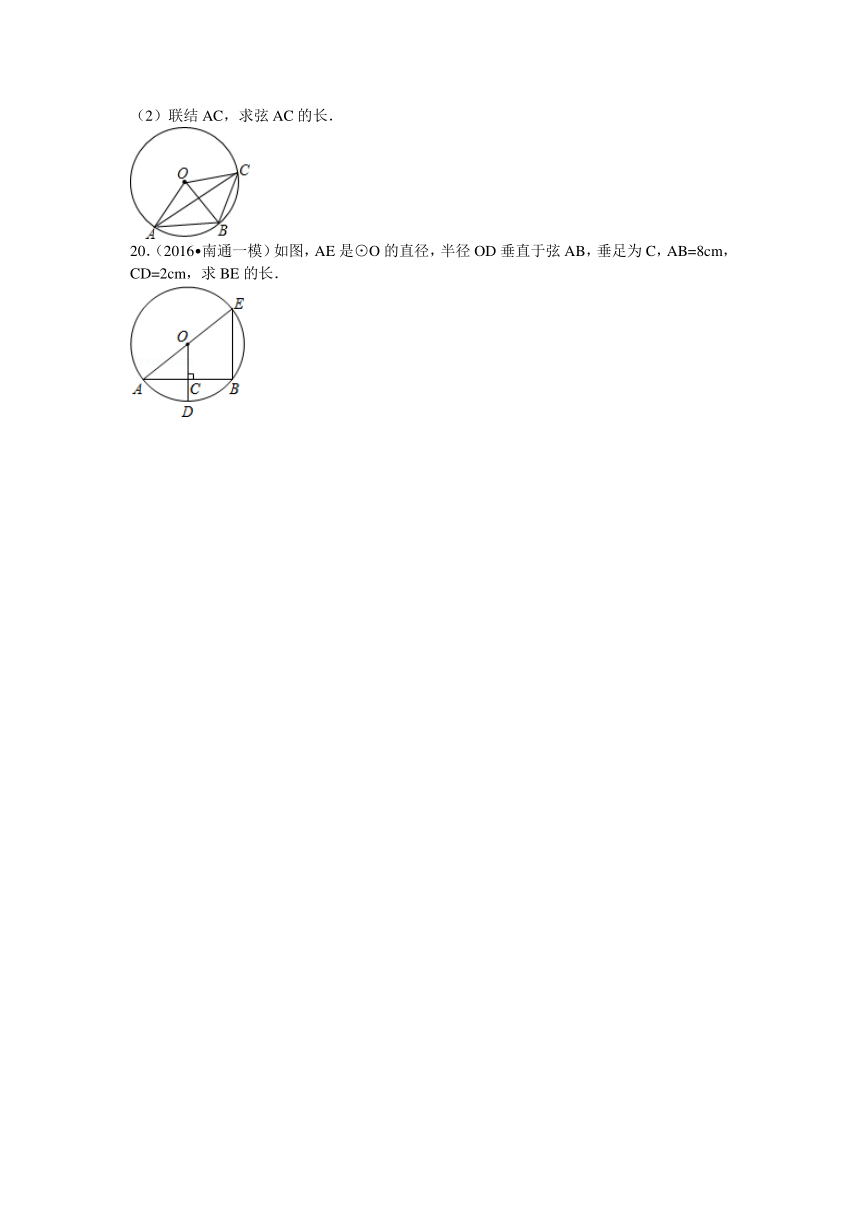
20.(2016 南通一模)如图,AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,求BE的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 牡丹江)如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3
B.2.5
C.4
D.3.5
【分析】连接OA,根据垂径定理得到AP=AB,利用勾股定理得到答案.
【解答】解:连接OA,
∵AB⊥OP,
∴AP==3,∠APO=90°,又OA=5,
∴OP===4,
故选C.
【点评】本题考查的是垂径定理的应用,掌握垂直于弦的直径平分这条弦是解题的关键.
2.(2016 黄石)如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5
B.7
C.9
D.11
【分析】根据⊙O的半径为13,弦AB的长度是24,ON⊥AB,可以求得AN的长,从而可以求得ON的长.
【解答】解:由题意可得,
OA=13,∠ONA=90°,AB=24,
∴AN=12,
∴ON=,
故选A.
【点评】本题考查垂径定理,解题的关键是明确垂径定理的内容,利用垂径定理解答问题.
3.(2016 黔南州)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
A.cm
B.3cm
C.3cm
D.6cm
【分析】根据垂径定理知圆心O到弦CD的距离为OE;由圆周角定理知∠COB=2∠CDB=60°,已知半径OC的长,即可在Rt△OCE中求OE的长度.
【解答】解:连接CB.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴圆心O到弦CD的距离为OE;
∵∠COB=2∠CDB(同弧所对的圆周角是所对的圆心角的一半),∠CDB=30°,
∴∠COB=60°;
在Rt△OCE中,
OC=5cm,OE=OC cos∠COB,
∴OE=cm.
故选A.
【点评】本题考查了垂径定理、圆周角定理及解直角三角形的综合应用.解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.
4.(2016 三明)如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A.2
B.3
C.4
D.5
【分析】根据垂径定理由OC⊥AB得到AD=AB=4,再根据勾股定理开始出OD,然后用OC﹣OD即可得到DC.
【解答】解:∵OC⊥AB,
∴AD=BD=AB=×8=4,
在Rt△OAD中,OA=5,AD=4,
∴OD==3,
∴CD=OC﹣OD=5﹣3=2.
故选A.
【点评】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
5.(2016 安徽校级自主招生)如图,AB是⊙O的弦,C是AB的三等分点,连接OC并延长交⊙O于点D.若OC=3,CD=2,则圆心O到弦AB的距离是( )
A.6
B.9﹣
C.
D.25﹣3
【分析】过圆心O作弦的垂线,垂足为G,得到Rt△OBG和Rt△OCG,在这两个三角形中用勾股定理计算可以求出OG的值,也就是圆心到弦的距离.
【解答】解:如图:过O作OG⊥AB于G,根据垂径定理有:AG=BG,
设AC=2a,则CB=4a,CG=a,GB=3a,
在Rt△OCG中,OC2=OG2+CG2=OG2+a2①
在Rt△OBG中,OB2=OG2+GB2=OG2+9a2②
又OC=3,OB=5,代入①②中,解方程得:a2=2,OG2=7.
所以圆心到弦的距离是.
故选C.
【点评】本题考查的是垂径定理,过圆心作圆的垂线,得到直角三角形,运用勾股定理计算可以求出圆心到弦的距离.
6.(2016 桐城市模拟)一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )
A.0.5
B.1
C.2
D.4
【分析】根据题意知,已知弦长和弓形高,求半径(直径).根据垂径定理和勾股定理求解.
【解答】解:设半径为r,过O作OE⊥AB交AB于点D,连接OA、OB,
则AD=AB=×0.8=0.4米,
设OA=r,则OD=r﹣DE=r﹣0.2,
在Rt△OAD中,
OA2=AD2+OD2,即r2=0.42+(r﹣0.2)2,解得r=0.5米,
故此输水管道的直径=2r=2×0.5=1米.
故选B.
【点评】本题考查的是垂径定理,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.
7.(2016 新泰市二模)如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )
A.8cm
B.16cm
C.8cm
D.16cm
【分析】连接OA、OC.设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.根据垂径定理,得CG=10.在直角三角形OCG中,根据勾股定理求得R的值,再进一步在直角三角形OAE中,根据勾股定理求得AE的长,从而再根据垂径定理即可求得AB的长.
【解答】解:如图所示,连接OA、OC.
设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.
∵OF⊥CD,
∴CG=CD=10cm.
在直角三角形COG中,根据勾股定理,得
R2=102+(R﹣2)2,
解,得R=26.
在直角三角形AOE中,根据勾股定理,得
AE==8cm.
根据垂径定理,得AB=16(cm),
故选B.
【点评】本题考查了勾股定理,垂径定理的应用,能构造直角三角形是解此题的关键,注意:垂直于弦的直径平分弦.
8.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
【分析】由垂径定理,可得AD=AB,然后由勾股定理求得OD的长,继而求得中间柱CD的高度.
【解答】解:∵CD是中间柱,
即=,
∴OC⊥AB,
∴AD=BD=AB=×16=8(m),
∵半径OA=10m,
在Rt△AOD中,OD==6(m),
∴CD=OC﹣OD=10﹣6=4(m).
故选B.
【点评】此题考查了垂径定理的应用与勾股定理.此题比较简单,注意数形结合思想的应用.
9.(2016 永康市模拟)如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为( )
A.m
B.2m
C.4m
D.6m
【分析】连接OA,根据桥拱半径OC为4m,求出OA=4m,根据CD=6m,求出OD=2m,根据AD=求出AD,最后根据AB=2AD即可得出答案.
【解答】解:连接OA,
∵桥拱半径OC为4m,
∴OA=4m,
∵CD=6m,
∴OD=8=6﹣4=2m,
∴AD===2m,
∴AB=2AD=2×2=4(m);
故选C.
【点评】此题考查了垂径定理的应用,关键是根据题意做出辅助线,用到的知识点是垂径定理、勾股定理.
10.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
【分析】连接OA,过点O作OD⊥AB于点D,由垂径定理可知,AD=AB=(9﹣1)=4,设OA=r,则OD=r﹣3,在Rt△OAD中利用勾股定理求出r的值即可.
【解答】解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=AB=(9﹣1)=4cm,
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=cm.
故选:C.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
二.填空题(共4小题)
11.(2016 安顺)如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE= 4﹣ .
【分析】连接OC,根据垂径定理得出CE=ED=CD=3,然后在Rt△OEC中由勾股定理求出OE的长度,最后由BE=OB﹣OE,即可求出BE的长度.
【解答】解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB﹣OE=4﹣.
故答案为4﹣.
【点评】本题主要考查了垂径定理,勾股定理等知识,关键在于熟练的运用垂径定理得出CE、ED的长度.
12.(2016 贵阳)如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是 .
【分析】作OM⊥AB于M,由垂径定理得出AM=BM=AB=4cm,由勾股定理求出OM,再由三角函数的定义即可得出结果.
【解答】解:作OM⊥AB于M,如图所示:
则AM=BM=AB=4cm,
∴OM===2(cm),
∵PM=PB+BM=6cm,
∴tan∠OPA===;
故答案为:.
【点评】本题考查了垂径定理、解直角三角形、勾股定理、三角函数的定义;熟练掌握垂径定理,由勾股定理求出OM是解决问题的关键.
13.(2016 海口校级一模)如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是 520
cm.
【分析】连接OF,交AC于点E,设圆O的半径为R,根据勾股定理列出方程,解方程即可.
【解答】解:连接OF,交AC于点E,
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AD∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE===100,
OE=R﹣AB=R﹣20,
∵AE2+OE2=OA2,
∴1002+(R﹣20)2=R2,
解得,R=260.
260×2=520(cm).
故答案为:520.
【点评】本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.
14.(2015 六盘水)赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 25 米.
【分析】根据垂径定理和勾股定理求解即可.
【解答】解:根据垂径定理,得AD=AB=20米.
设圆的半径是r,根据勾股定理,
得R2=202+(R﹣10)2,
解得R=25(米).
故答案为25.
【点评】此题综合运用了勾股定理以及垂径定理.注意构造由半径、半弦、弦心距组成的直角三角形进行有关的计算.
三.解答题(共6小题)
15.(2016 西安校级三模)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
【分析】(1)要证明:E是OB的中点,只要求证OE=OB=OC,即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,,
∴,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,
∴,
又∵BE=OE,
∴OE=2,
∴,
∴.
【点评】解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
16.(2016 黄冈校级自主招生)如图,在⊙O中,弦CD垂直于直径AB.M是OC的中点,AM的延长线交⊙O于E,DE交BC于N.求证:BN=CN.
【分析】连接AC和BD,根据垂径定理得BC=BD,再由已知条件可以证得△BCD∽△OCA,则=,还可以证明△CDN∽△CAM.有相似三角形的性质,证出BN=CN.
【解答】证明:连接AC和BD.
∵弦CD垂直于直径AB,
∴BC=BD.(5分)
∴∠BCD=∠BDC.
∵OA=OC,
∴∠OCA=∠OAC.
∵∠BDC=∠OAC,
∴∠BCD=∠OCA.
∴△BCD∽△OCA.
∴=(15分)
在△CDN和△CAM中,
∵∠DCN=∠ACM,∠CDN=∠CAM,
∴△CDN∽△CAM.(20分)
∵===,
∴CN=CB,即BN=CN.(25分)
【点评】本题考查了相似三角形的判定和性质、垂径定理,解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
【分析】(1)先根据垂径定理得出E为CD的中点,再由勾股定理即可得出结论;
(2)先由锐角三角函数的定义求出EF的长,再分点F在线段CD的上方与下方两种情况进行讨论即可.
【解答】解:(1)∵AB为直径,点B为的中点,CD=2,
∴AB⊥CD,
∴DE=CD=.
在Rt△ODE中,
∵OD=r,OE=5﹣r,DE=,
∴r2=(5﹣r)2+()2,解得r=3;
(2)∵由(1)知,OE=AE﹣AO=5﹣3=2,
∴tan∠FCE=tan∠DOB==.
在Rt△FCE中,
∵==,
∴EF=,
∴当点F在线段CD的上方时,AF=AE﹣EF=5﹣=;
当点F在线段CD的下方时,AF=AE+EF=5+=>AB,不合题意.
综上所述,AF=.
【点评】本题考查的是垂径定理,熟知垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
18.(2016 槐荫区二模)如图,已知⊙O的半径为15,弦AB=24,求点O到AB的距离及∠OAB的余弦值.
【分析】过O作OC⊥AB,可得C为AB的中点,求出AC的长,根据勾股定理求出OC的长,在Rt△AOC中,利用锐角三角函数的定义即可得出结论.
【解答】解:过O作OC⊥AB,可得C为AB的中点,
∵AB=24,
∴AC=BC=12,
∴OC===9.
在Rt△AOC中,OA=15,AC=12,
则cos∠OAB==.
【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.(2016 嘉定区一模)已知:如图,已知点A、B、C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=时.
(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
【分析】(1)过O作OH⊥AB于H,根据cos∠OAB=,得到,求得AH=3cm,OH=4cm,AB=2AH=6cm,根据三角形的面积公式即可实施激励;
(2)设AC交OB于M,由B是的中点,得到,求出AB=BC,推出OB垂直平分AC,即可得到结论.
【解答】解:(1)过O作OH⊥AB于H,
∵cos∠OAB=,
∴,
∴AH=3cm,OH=4cm,AB=2AH=6cm,
∴S△OAB=AB OH=12cm2;
(2)设AC交OB于M,∵B是的中点,
∴,∴AB=BC,
∵OA=OC,
故O,B均在线段AC的垂直平分线上,
∴OB垂直平分AC,
∴AM=AB sin∠MBA=6×=,
∴AC=2AM=cm.
【点评】本题考查了垂径定理,解直角三角形,线段垂直平分线的判定和性质,正确的作出辅助线构造直角三角形是解题的关键.
20.(2016 南通一模)如图,AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,求BE的长.
【分析】根据垂径定理可得AC=4cm,然后设CO=xcm,则DO=AO=(x+2)cm,再利用勾股定理可得(x+2)2=42+x2,解出x的值,再根据三角形中位线定理可得答案.
【解答】解:∵半径OD垂直于弦AB,垂足为C,AB=8cm,
∴AC=4cm,
设CO=xcm,则DO=AO=(x+2)cm,
在Rt△AOC中:AO2=CO2+AC2,
∴(x+2)2=42+x2,
解得:x=3,
∵AO=EO,AC=CB,
∴BE=2CO=6cm.
【点评】此题主要考查了垂径定理、勾股定理,以及三角形的中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半;垂直弦的直径平分这条弦,并且平分弦所对的两条弧.
一.选择题(共10小题)
1.(2016 牡丹江)如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3
B.2.5
C.4
D.3.5
2.(2016 黄石)如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5
B.7
C.9
D.11
3.(2016 黔南州)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
A.cm
B.3cm
C.3cm
D.6cm
4.(2016 三明)如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A.2
B.3
C.4
D.5
5.(2016 安徽校级自主招生)如图,AB是⊙O的弦,C是AB的三等分点,连接OC并延长交⊙O于点D.若OC=3,CD=2,则圆心O到弦AB的距离是( )
A.6
B.9﹣
C.
D.25﹣3
6.(2016 桐城市模拟)一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )
A.0.5
B.1
C.2
D.4
7.(2016 新泰市二模)如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )
A.8cm
B.16cm
C.8cm
D.16cm
8.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
9.(2016 永康市模拟)如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为( )
A.m
B.2m
C.4m
D.6m
10.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
二.填空题(共4小题)
11.(2016 安顺)如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=______.
12.(2016 贵阳)如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是______.
13.(2016 海口校级一模)如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是______
cm.
14.(2015 六盘水)赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=______米.
三.解答题(共6小题)
15.(2016 西安校级三模)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
16.(2016 黄冈校级自主招生)如图,在⊙O中,弦CD垂直于直径AB.M是OC的中点,AM的延长线交⊙O于E,DE交BC于N.求证:BN=CN.
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
18.(2016 槐荫区二模)如图,已知⊙O的半径为15,弦AB=24,求点O到AB的距离及∠OAB的余弦值.
19.(2016 嘉定区一模)已知:如图,已知点A、B、C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=时.
(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
20.(2016 南通一模)如图,AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,求BE的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 牡丹江)如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3
B.2.5
C.4
D.3.5
【分析】连接OA,根据垂径定理得到AP=AB,利用勾股定理得到答案.
【解答】解:连接OA,
∵AB⊥OP,
∴AP==3,∠APO=90°,又OA=5,
∴OP===4,
故选C.
【点评】本题考查的是垂径定理的应用,掌握垂直于弦的直径平分这条弦是解题的关键.
2.(2016 黄石)如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5
B.7
C.9
D.11
【分析】根据⊙O的半径为13,弦AB的长度是24,ON⊥AB,可以求得AN的长,从而可以求得ON的长.
【解答】解:由题意可得,
OA=13,∠ONA=90°,AB=24,
∴AN=12,
∴ON=,
故选A.
【点评】本题考查垂径定理,解题的关键是明确垂径定理的内容,利用垂径定理解答问题.
3.(2016 黔南州)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
A.cm
B.3cm
C.3cm
D.6cm
【分析】根据垂径定理知圆心O到弦CD的距离为OE;由圆周角定理知∠COB=2∠CDB=60°,已知半径OC的长,即可在Rt△OCE中求OE的长度.
【解答】解:连接CB.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴圆心O到弦CD的距离为OE;
∵∠COB=2∠CDB(同弧所对的圆周角是所对的圆心角的一半),∠CDB=30°,
∴∠COB=60°;
在Rt△OCE中,
OC=5cm,OE=OC cos∠COB,
∴OE=cm.
故选A.
【点评】本题考查了垂径定理、圆周角定理及解直角三角形的综合应用.解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.
4.(2016 三明)如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A.2
B.3
C.4
D.5
【分析】根据垂径定理由OC⊥AB得到AD=AB=4,再根据勾股定理开始出OD,然后用OC﹣OD即可得到DC.
【解答】解:∵OC⊥AB,
∴AD=BD=AB=×8=4,
在Rt△OAD中,OA=5,AD=4,
∴OD==3,
∴CD=OC﹣OD=5﹣3=2.
故选A.
【点评】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
5.(2016 安徽校级自主招生)如图,AB是⊙O的弦,C是AB的三等分点,连接OC并延长交⊙O于点D.若OC=3,CD=2,则圆心O到弦AB的距离是( )
A.6
B.9﹣
C.
D.25﹣3
【分析】过圆心O作弦的垂线,垂足为G,得到Rt△OBG和Rt△OCG,在这两个三角形中用勾股定理计算可以求出OG的值,也就是圆心到弦的距离.
【解答】解:如图:过O作OG⊥AB于G,根据垂径定理有:AG=BG,
设AC=2a,则CB=4a,CG=a,GB=3a,
在Rt△OCG中,OC2=OG2+CG2=OG2+a2①
在Rt△OBG中,OB2=OG2+GB2=OG2+9a2②
又OC=3,OB=5,代入①②中,解方程得:a2=2,OG2=7.
所以圆心到弦的距离是.
故选C.
【点评】本题考查的是垂径定理,过圆心作圆的垂线,得到直角三角形,运用勾股定理计算可以求出圆心到弦的距离.
6.(2016 桐城市模拟)一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )
A.0.5
B.1
C.2
D.4
【分析】根据题意知,已知弦长和弓形高,求半径(直径).根据垂径定理和勾股定理求解.
【解答】解:设半径为r,过O作OE⊥AB交AB于点D,连接OA、OB,
则AD=AB=×0.8=0.4米,
设OA=r,则OD=r﹣DE=r﹣0.2,
在Rt△OAD中,
OA2=AD2+OD2,即r2=0.42+(r﹣0.2)2,解得r=0.5米,
故此输水管道的直径=2r=2×0.5=1米.
故选B.
【点评】本题考查的是垂径定理,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.
7.(2016 新泰市二模)如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )
A.8cm
B.16cm
C.8cm
D.16cm
【分析】连接OA、OC.设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.根据垂径定理,得CG=10.在直角三角形OCG中,根据勾股定理求得R的值,再进一步在直角三角形OAE中,根据勾股定理求得AE的长,从而再根据垂径定理即可求得AB的长.
【解答】解:如图所示,连接OA、OC.
设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.
∵OF⊥CD,
∴CG=CD=10cm.
在直角三角形COG中,根据勾股定理,得
R2=102+(R﹣2)2,
解,得R=26.
在直角三角形AOE中,根据勾股定理,得
AE==8cm.
根据垂径定理,得AB=16(cm),
故选B.
【点评】本题考查了勾股定理,垂径定理的应用,能构造直角三角形是解此题的关键,注意:垂直于弦的直径平分弦.
8.(2016 银川校级一模)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
A.6
B.4
C.8
D.5
【分析】由垂径定理,可得AD=AB,然后由勾股定理求得OD的长,继而求得中间柱CD的高度.
【解答】解:∵CD是中间柱,
即=,
∴OC⊥AB,
∴AD=BD=AB=×16=8(m),
∵半径OA=10m,
在Rt△AOD中,OD==6(m),
∴CD=OC﹣OD=10﹣6=4(m).
故选B.
【点评】此题考查了垂径定理的应用与勾股定理.此题比较简单,注意数形结合思想的应用.
9.(2016 永康市模拟)如图,圆弧形石拱桥的桥顶到水面的距离CD为6m,桥拱半径OC为4m,则水面宽AB为( )
A.m
B.2m
C.4m
D.6m
【分析】连接OA,根据桥拱半径OC为4m,求出OA=4m,根据CD=6m,求出OD=2m,根据AD=求出AD,最后根据AB=2AD即可得出答案.
【解答】解:连接OA,
∵桥拱半径OC为4m,
∴OA=4m,
∵CD=6m,
∴OD=8=6﹣4=2m,
∴AD===2m,
∴AB=2AD=2×2=4(m);
故选C.
【点评】此题考查了垂径定理的应用,关键是根据题意做出辅助线,用到的知识点是垂径定理、勾股定理.
10.(2015 滕州市校级四模)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm)那么该圆的半径为( )
A.8cm
B.9cm
C.cm
D.10cm
【分析】连接OA,过点O作OD⊥AB于点D,由垂径定理可知,AD=AB=(9﹣1)=4,设OA=r,则OD=r﹣3,在Rt△OAD中利用勾股定理求出r的值即可.
【解答】解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=AB=(9﹣1)=4cm,
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=cm.
故选:C.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
二.填空题(共4小题)
11.(2016 安顺)如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE= 4﹣ .
【分析】连接OC,根据垂径定理得出CE=ED=CD=3,然后在Rt△OEC中由勾股定理求出OE的长度,最后由BE=OB﹣OE,即可求出BE的长度.
【解答】解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB﹣OE=4﹣.
故答案为4﹣.
【点评】本题主要考查了垂径定理,勾股定理等知识,关键在于熟练的运用垂径定理得出CE、ED的长度.
12.(2016 贵阳)如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是 .
【分析】作OM⊥AB于M,由垂径定理得出AM=BM=AB=4cm,由勾股定理求出OM,再由三角函数的定义即可得出结果.
【解答】解:作OM⊥AB于M,如图所示:
则AM=BM=AB=4cm,
∴OM===2(cm),
∵PM=PB+BM=6cm,
∴tan∠OPA===;
故答案为:.
【点评】本题考查了垂径定理、解直角三角形、勾股定理、三角函数的定义;熟练掌握垂径定理,由勾股定理求出OM是解决问题的关键.
13.(2016 海口校级一模)如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是 520
cm.
【分析】连接OF,交AC于点E,设圆O的半径为R,根据勾股定理列出方程,解方程即可.
【解答】解:连接OF,交AC于点E,
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AD∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE===100,
OE=R﹣AB=R﹣20,
∵AE2+OE2=OA2,
∴1002+(R﹣20)2=R2,
解得,R=260.
260×2=520(cm).
故答案为:520.
【点评】本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.
14.(2015 六盘水)赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 25 米.
【分析】根据垂径定理和勾股定理求解即可.
【解答】解:根据垂径定理,得AD=AB=20米.
设圆的半径是r,根据勾股定理,
得R2=202+(R﹣10)2,
解得R=25(米).
故答案为25.
【点评】此题综合运用了勾股定理以及垂径定理.注意构造由半径、半弦、弦心距组成的直角三角形进行有关的计算.
三.解答题(共6小题)
15.(2016 西安校级三模)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
【分析】(1)要证明:E是OB的中点,只要求证OE=OB=OC,即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,,
∴,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,
∴,
又∵BE=OE,
∴OE=2,
∴,
∴.
【点评】解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
16.(2016 黄冈校级自主招生)如图,在⊙O中,弦CD垂直于直径AB.M是OC的中点,AM的延长线交⊙O于E,DE交BC于N.求证:BN=CN.
【分析】连接AC和BD,根据垂径定理得BC=BD,再由已知条件可以证得△BCD∽△OCA,则=,还可以证明△CDN∽△CAM.有相似三角形的性质,证出BN=CN.
【解答】证明:连接AC和BD.
∵弦CD垂直于直径AB,
∴BC=BD.(5分)
∴∠BCD=∠BDC.
∵OA=OC,
∴∠OCA=∠OAC.
∵∠BDC=∠OAC,
∴∠BCD=∠OCA.
∴△BCD∽△OCA.
∴=(15分)
在△CDN和△CAM中,
∵∠DCN=∠ACM,∠CDN=∠CAM,
∴△CDN∽△CAM.(20分)
∵===,
∴CN=CB,即BN=CN.(25分)
【点评】本题考查了相似三角形的判定和性质、垂径定理,解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解.
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
【分析】(1)先根据垂径定理得出E为CD的中点,再由勾股定理即可得出结论;
(2)先由锐角三角函数的定义求出EF的长,再分点F在线段CD的上方与下方两种情况进行讨论即可.
【解答】解:(1)∵AB为直径,点B为的中点,CD=2,
∴AB⊥CD,
∴DE=CD=.
在Rt△ODE中,
∵OD=r,OE=5﹣r,DE=,
∴r2=(5﹣r)2+()2,解得r=3;
(2)∵由(1)知,OE=AE﹣AO=5﹣3=2,
∴tan∠FCE=tan∠DOB==.
在Rt△FCE中,
∵==,
∴EF=,
∴当点F在线段CD的上方时,AF=AE﹣EF=5﹣=;
当点F在线段CD的下方时,AF=AE+EF=5+=>AB,不合题意.
综上所述,AF=.
【点评】本题考查的是垂径定理,熟知垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
18.(2016 槐荫区二模)如图,已知⊙O的半径为15,弦AB=24,求点O到AB的距离及∠OAB的余弦值.
【分析】过O作OC⊥AB,可得C为AB的中点,求出AC的长,根据勾股定理求出OC的长,在Rt△AOC中,利用锐角三角函数的定义即可得出结论.
【解答】解:过O作OC⊥AB,可得C为AB的中点,
∵AB=24,
∴AC=BC=12,
∴OC===9.
在Rt△AOC中,OA=15,AC=12,
则cos∠OAB==.
【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.(2016 嘉定区一模)已知:如图,已知点A、B、C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=时.
(1)求△OAB的面积;
(2)联结AC,求弦AC的长.
【分析】(1)过O作OH⊥AB于H,根据cos∠OAB=,得到,求得AH=3cm,OH=4cm,AB=2AH=6cm,根据三角形的面积公式即可实施激励;
(2)设AC交OB于M,由B是的中点,得到,求出AB=BC,推出OB垂直平分AC,即可得到结论.
【解答】解:(1)过O作OH⊥AB于H,
∵cos∠OAB=,
∴,
∴AH=3cm,OH=4cm,AB=2AH=6cm,
∴S△OAB=AB OH=12cm2;
(2)设AC交OB于M,∵B是的中点,
∴,∴AB=BC,
∵OA=OC,
故O,B均在线段AC的垂直平分线上,
∴OB垂直平分AC,
∴AM=AB sin∠MBA=6×=,
∴AC=2AM=cm.
【点评】本题考查了垂径定理,解直角三角形,线段垂直平分线的判定和性质,正确的作出辅助线构造直角三角形是解题的关键.
20.(2016 南通一模)如图,AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,求BE的长.
【分析】根据垂径定理可得AC=4cm,然后设CO=xcm,则DO=AO=(x+2)cm,再利用勾股定理可得(x+2)2=42+x2,解出x的值,再根据三角形中位线定理可得答案.
【解答】解:∵半径OD垂直于弦AB,垂足为C,AB=8cm,
∴AC=4cm,
设CO=xcm,则DO=AO=(x+2)cm,
在Rt△AOC中:AO2=CO2+AC2,
∴(x+2)2=42+x2,
解得:x=3,
∵AO=EO,AC=CB,
∴BE=2CO=6cm.
【点评】此题主要考查了垂径定理、勾股定理,以及三角形的中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半;垂直弦的直径平分这条弦,并且平分弦所对的两条弧.
