2.4基本初等函数单元测验 同步训练(含答案)
文档属性
| 名称 | 2.4基本初等函数单元测验 同步训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 73.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-08 00:00:00 | ||
图片预览



文档简介
2.4基本初等函数单元测验 同步训练(含答案)
一、选择题
1.的值等于( )
A.lg11-1 B.1-lg11 C.11 D.0.1
2.化简(mn)(-3mn)÷()的结果是( )
A.6m B.-m C.-9m D.9m2
3.函数f(x)=+lg(3x+1)的定义域为( )
A.(-5,+∞) B.[-5,+∞) C.(-5,0) D.(-2,0)
4.函数y=ax-b(a>0,a≠1,b>2)的图象可能是( )
5.已知函数f(x)=3|x|,g(x)=ax2-x(a∈R).若f[g(1)]=1,则a=( )
A.1 B.2 C.3 D.-1
6.设a=0.70.7,b=0.71.4,c=1.40.7,则a,b,c的大小关系是( )
A.a7.函数f(x)=2ln(x2+1)的图象大致是( )
8.已知函数f(x)是奇函数,当x>0时,f(x)=ax(a>0,a≠1),且f(log4)=-3,则a的值为( )21世纪教育网版权所有
A. B.3 C.9 D.
9.设a=log45,b=log54,c=log35,则( )
A.a>c>b B.b>c>a C.c>b>a D.c>a>b
10.已知定义在R上的函数f(x)=2|x-a|-1(a为实数)为偶函数.且p=f(log0.53),q=f(log25),s=f(2a),则p,q,s的大小关系为( )
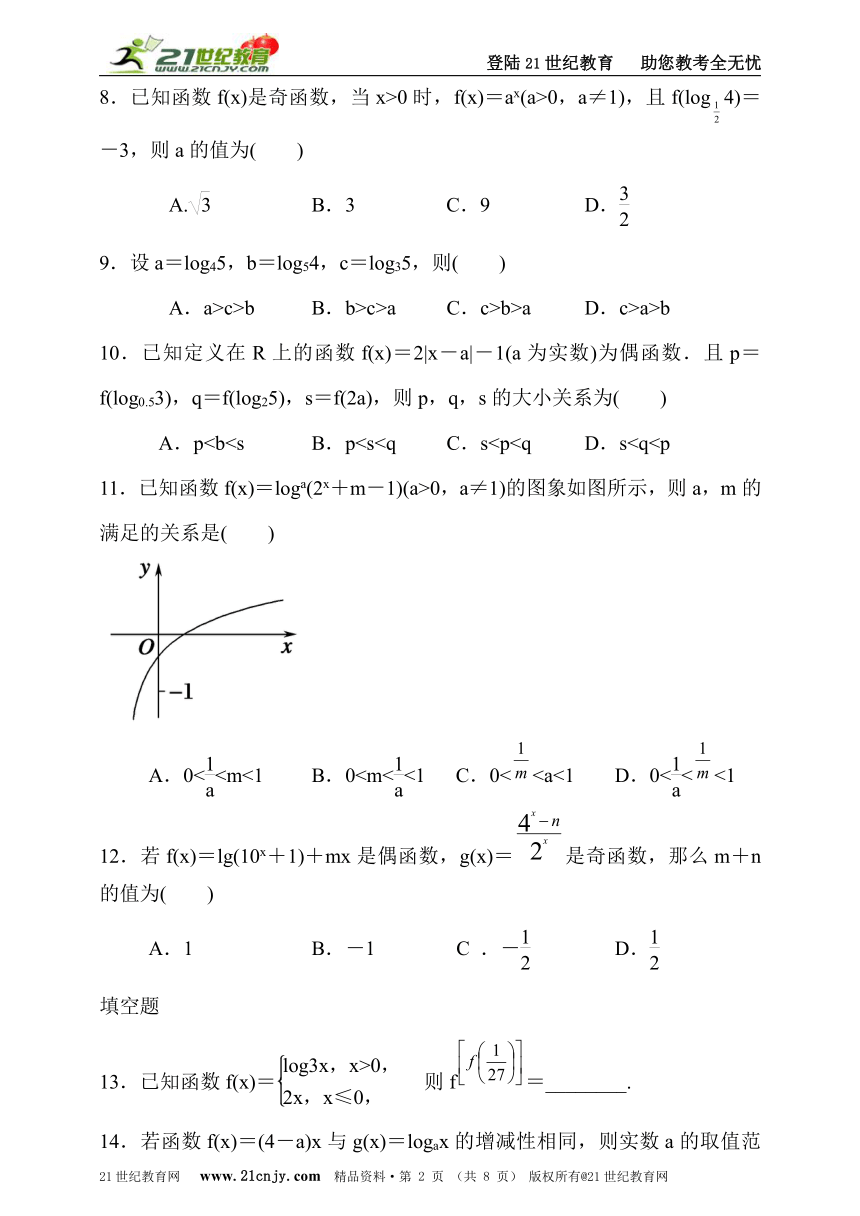
A.p11.已知函数f(x)=loga(2x+m-1)(a>0,a≠1)的图象如图所示,则a,m的满足的关系是( )2·1·c·n·j·y
A.0<12.若f(x)=lg(10x+1)+mx是偶函数,g(x)=是奇函数,那么m+n的值为( )
A.1 B.-1 C .- D.
填空题
13.已知函数f(x)=则f=________.
14.若函数f(x)=(4-a)x与g(x)=logax的增减性相同,则实数a的取值范围是________.www-2-1-cnjy-com
15.下列区间中,函数f(x)=|ln(2-x)|在其上为增函数的是________.(填序号)①(-∞,1]; ②[0,); ③[-1,]; ④[1,2). 21*cnjy*com
16.已知a>0,b>0,ab=4,则当a的值为________时,log2a·log2(2b)取得最大值.21教育名师原创作品
解答题
17.求值:
(1)()0+2-2·|-0.064|-();
(2)(log32+log92)·(log43+log83)+(log33)2+ln-lg100.
18.已知函数f(x)=xα-且f(4)=.
(1)求α的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
19.设f(x)=log(10-mx),m为常数.若f(3)=-2.
(1)求m的值;
(2)求使f(x)≥0的x的取值范围;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>()x+t恒成立,求实数t的取值范围.21教育网
20.已知函数f(x)=2x2-4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[-1,2k]上不具有单调性,求实数k的取值范围;
(2)若f(1)=g(1).①求实数a的值;
②设t1=f(x),t2=g(x),t3=2x,当x∈(0,1)时,试比较t1,t2,t3的大小.
参考答案:
1.解析:因为lg11>lg10=1,所以=|1-lg11|=lg11-1.故选A.答案:A
2.解析:原式=-9m+-n+-=-9mn0=-9m.答案:C
3.解析:因为所以x>-5,函数f(x)的定义域是(-5,+∞).
答案:A
4.解析:当x=0时,y=a0-b<0,排除A、C,b>2,所以函数图象向下移动超过2个单位.故选B.答案:Bwww.21-cn-jy.com
5.解析:因为f[g(1)]=1,且f(x)=3|x|,所以g(1)=0,即a·12-1=0,解得a=1.答案:A【来源:21·世纪·教育·网】
6.解析:由指数函数y=0.7x在(0,+∞)上单调递减,可知0.71.4<0.70.7,由幂函数y=x0.7在(0,+∞)上单调递增,可知0.70.7<1.40.7,所以b7.解析:函数过定点(0,0),排除选项B、D,又f(-x)=2ln(x2+1)=f(x),所以f(x)为偶函数.排除选项C.故选A.答案:A2-1-c-n-j-y
8.解析:当x<0时,-x>0,所以f(-x)=a-x,又f(x)为奇函数,f(-x)=-f(x),所以f(x)=-a-x(x<0),因为log4=-2<0,所以f(log4)=-a2=-3.所以a2=3.答案:A【来源:21cnj*y.co*m】
9.解析:易知log45>1,log54∈(0,1),log35∈(0,1),在同一平面直角坐标系中画出函数y=log4x与y=log3x的图象(图略),观察可知log45a>b.答案:D【出处:21教育名师】
10.解析:由f(x)=2|x-a|-1是偶函数得a=0,则f(x)=2|x|-1.
当x∈[0,+∞)时,f(x)=2x-1递增,又p=f(log0.53)=f(|log0.53|)=f(log23),s=f(0),且011.解析:由图象知函数单调递增,所以a>1,又-112.解析:函数f(x)=lg(10x+1)+mx是偶函数,所以f(x)=f(-x),即lg(10x+1)+mx=lg(10-x+1)-mx,化简得(2m+1)x=0对所有的x都成立,所以m=-;函数g(x)=是奇函数,所以g(-x)=-g(x),即=-,化简得(n-1)(4x+1)=0,所以n=1,故m+n=.答案:D
13.解析:f=log3=-3;所以f=f(-3)=2-3=.答案:
14.解析:由题意得或所以1答案:(1,2)
15.解析:将函数f(x)化为分段函数,得f(x)=
作出函数的图象如图所示,根据图象可知f(x)在[1,2)上为增函数,其他三个区间都不满足题意.
答案:④
16.解析:由于a>0,b>0,ab=4,所以a=,所以log2a·log2(2b)=log2·log2(2b)=(2-log2b)·(1+log2b)=-(log2b)2+log2b+3=-(log2b-)2+,当b=时,有最大值,此时a=16.答案:16【版权所有:21教育】
17.解:(1)原式=1+×-=-.
(2)原式=(+)·(+)++-2=·+-2=+-2=0.
18.解:(1)因为f(4)=,所以4α-=,所以α=1.
(2)由(1)知f(x)=x-,所以函数的定义域为(-∞,0)∪(0,+∞),关于原点对称.又f(-x)=-x+=-=-f(x).所以函数f(x)是奇函数.
(3)函数f(x)在(0,+∞)上是单调增函数,证明如下:设x1>x2>0,
则f(x1)-f(x2)=x1--=(x1-x2),因为x1>x2>0,
所以x1-x2>0,1+>0.所以f(x1)>f(x2).所以函数f(x)在(0,+∞)上为单调增函数.21cnjy.com
19.解:(1)∵f(3)=-2,∴log(10-3m)=-2.即10-3m=()-2,∴m=2.21·cn·jy·com
(2)∵f(x)=log(10-2x)≥0,∴10-2x≤1.又10-2x>0,∴x∈[,5).
(3)设g(x)=log(10-2x)-()x.由题意知g(x)>t在x∈[3,4]上恒成立,
∵g(x)在[3,4]上为增函数,∴t20.解:(1)因为抛物线y=2x2-4x+a开口向上,对称轴为x=1.
所以函数f(x)在(-∞,1]上单调递减,在[1,+∞)上单调递增,
因为函数f(x)在[-1,2m]上不单调,所以2m>1,得m>,
所以实数m的取值范围为.
(2)①因为f(1)=g(1),所以-2+a=0,所以实数a的值为2.
②因为t1=f(x)=x2-2x+1=(x-1)2,t2=g(x)=log2x,t3=2x,
所以当x∈(0,1)时,t1∈(0,1),t2∈(-∞,0),t3∈(1,2),所以t2
一、选择题
1.的值等于( )
A.lg11-1 B.1-lg11 C.11 D.0.1
2.化简(mn)(-3mn)÷()的结果是( )
A.6m B.-m C.-9m D.9m2
3.函数f(x)=+lg(3x+1)的定义域为( )
A.(-5,+∞) B.[-5,+∞) C.(-5,0) D.(-2,0)
4.函数y=ax-b(a>0,a≠1,b>2)的图象可能是( )
5.已知函数f(x)=3|x|,g(x)=ax2-x(a∈R).若f[g(1)]=1,则a=( )
A.1 B.2 C.3 D.-1
6.设a=0.70.7,b=0.71.4,c=1.40.7,则a,b,c的大小关系是( )
A.a
8.已知函数f(x)是奇函数,当x>0时,f(x)=ax(a>0,a≠1),且f(log4)=-3,则a的值为( )21世纪教育网版权所有
A. B.3 C.9 D.
9.设a=log45,b=log54,c=log35,则( )
A.a>c>b B.b>c>a C.c>b>a D.c>a>b
10.已知定义在R上的函数f(x)=2|x-a|-1(a为实数)为偶函数.且p=f(log0.53),q=f(log25),s=f(2a),则p,q,s的大小关系为( )
A.p
A.0<
A.1 B.-1 C .- D.
填空题
13.已知函数f(x)=则f=________.
14.若函数f(x)=(4-a)x与g(x)=logax的增减性相同,则实数a的取值范围是________.www-2-1-cnjy-com
15.下列区间中,函数f(x)=|ln(2-x)|在其上为增函数的是________.(填序号)①(-∞,1]; ②[0,); ③[-1,]; ④[1,2). 21*cnjy*com
16.已知a>0,b>0,ab=4,则当a的值为________时,log2a·log2(2b)取得最大值.21教育名师原创作品
解答题
17.求值:
(1)()0+2-2·|-0.064|-();
(2)(log32+log92)·(log43+log83)+(log33)2+ln-lg100.
18.已知函数f(x)=xα-且f(4)=.
(1)求α的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
19.设f(x)=log(10-mx),m为常数.若f(3)=-2.
(1)求m的值;
(2)求使f(x)≥0的x的取值范围;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>()x+t恒成立,求实数t的取值范围.21教育网
20.已知函数f(x)=2x2-4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[-1,2k]上不具有单调性,求实数k的取值范围;
(2)若f(1)=g(1).①求实数a的值;
②设t1=f(x),t2=g(x),t3=2x,当x∈(0,1)时,试比较t1,t2,t3的大小.
参考答案:
1.解析:因为lg11>lg10=1,所以=|1-lg11|=lg11-1.故选A.答案:A
2.解析:原式=-9m+-n+-=-9mn0=-9m.答案:C
3.解析:因为所以x>-5,函数f(x)的定义域是(-5,+∞).
答案:A
4.解析:当x=0时,y=a0-b<0,排除A、C,b>2,所以函数图象向下移动超过2个单位.故选B.答案:Bwww.21-cn-jy.com
5.解析:因为f[g(1)]=1,且f(x)=3|x|,所以g(1)=0,即a·12-1=0,解得a=1.答案:A【来源:21·世纪·教育·网】
6.解析:由指数函数y=0.7x在(0,+∞)上单调递减,可知0.71.4<0.70.7,由幂函数y=x0.7在(0,+∞)上单调递增,可知0.70.7<1.40.7,所以b
8.解析:当x<0时,-x>0,所以f(-x)=a-x,又f(x)为奇函数,f(-x)=-f(x),所以f(x)=-a-x(x<0),因为log4=-2<0,所以f(log4)=-a2=-3.所以a2=3.答案:A【来源:21cnj*y.co*m】
9.解析:易知log45>1,log54∈(0,1),log35∈(0,1),在同一平面直角坐标系中画出函数y=log4x与y=log3x的图象(图略),观察可知log45
10.解析:由f(x)=2|x-a|-1是偶函数得a=0,则f(x)=2|x|-1.
当x∈[0,+∞)时,f(x)=2x-1递增,又p=f(log0.53)=f(|log0.53|)=f(log23),s=f(0),且0
13.解析:f=log3=-3;所以f=f(-3)=2-3=.答案:
14.解析:由题意得或所以1
15.解析:将函数f(x)化为分段函数,得f(x)=
作出函数的图象如图所示,根据图象可知f(x)在[1,2)上为增函数,其他三个区间都不满足题意.
答案:④
16.解析:由于a>0,b>0,ab=4,所以a=,所以log2a·log2(2b)=log2·log2(2b)=(2-log2b)·(1+log2b)=-(log2b)2+log2b+3=-(log2b-)2+,当b=时,有最大值,此时a=16.答案:16【版权所有:21教育】
17.解:(1)原式=1+×-=-.
(2)原式=(+)·(+)++-2=·+-2=+-2=0.
18.解:(1)因为f(4)=,所以4α-=,所以α=1.
(2)由(1)知f(x)=x-,所以函数的定义域为(-∞,0)∪(0,+∞),关于原点对称.又f(-x)=-x+=-=-f(x).所以函数f(x)是奇函数.
(3)函数f(x)在(0,+∞)上是单调增函数,证明如下:设x1>x2>0,
则f(x1)-f(x2)=x1--=(x1-x2),因为x1>x2>0,
所以x1-x2>0,1+>0.所以f(x1)>f(x2).所以函数f(x)在(0,+∞)上为单调增函数.21cnjy.com
19.解:(1)∵f(3)=-2,∴log(10-3m)=-2.即10-3m=()-2,∴m=2.21·cn·jy·com
(2)∵f(x)=log(10-2x)≥0,∴10-2x≤1.又10-2x>0,∴x∈[,5).
(3)设g(x)=log(10-2x)-()x.由题意知g(x)>t在x∈[3,4]上恒成立,
∵g(x)在[3,4]上为增函数,∴t
所以函数f(x)在(-∞,1]上单调递减,在[1,+∞)上单调递增,
因为函数f(x)在[-1,2m]上不单调,所以2m>1,得m>,
所以实数m的取值范围为.
(2)①因为f(1)=g(1),所以-2+a=0,所以实数a的值为2.
②因为t1=f(x)=x2-2x+1=(x-1)2,t2=g(x)=log2x,t3=2x,
所以当x∈(0,1)时,t1∈(0,1),t2∈(-∞,0),t3∈(1,2),所以t2
