沪科版九年级数学下册25.1.2《正投影及其性质》测试卷(含答案解析)
文档属性
| 名称 | 沪科版九年级数学下册25.1.2《正投影及其性质》测试卷(含答案解析) | 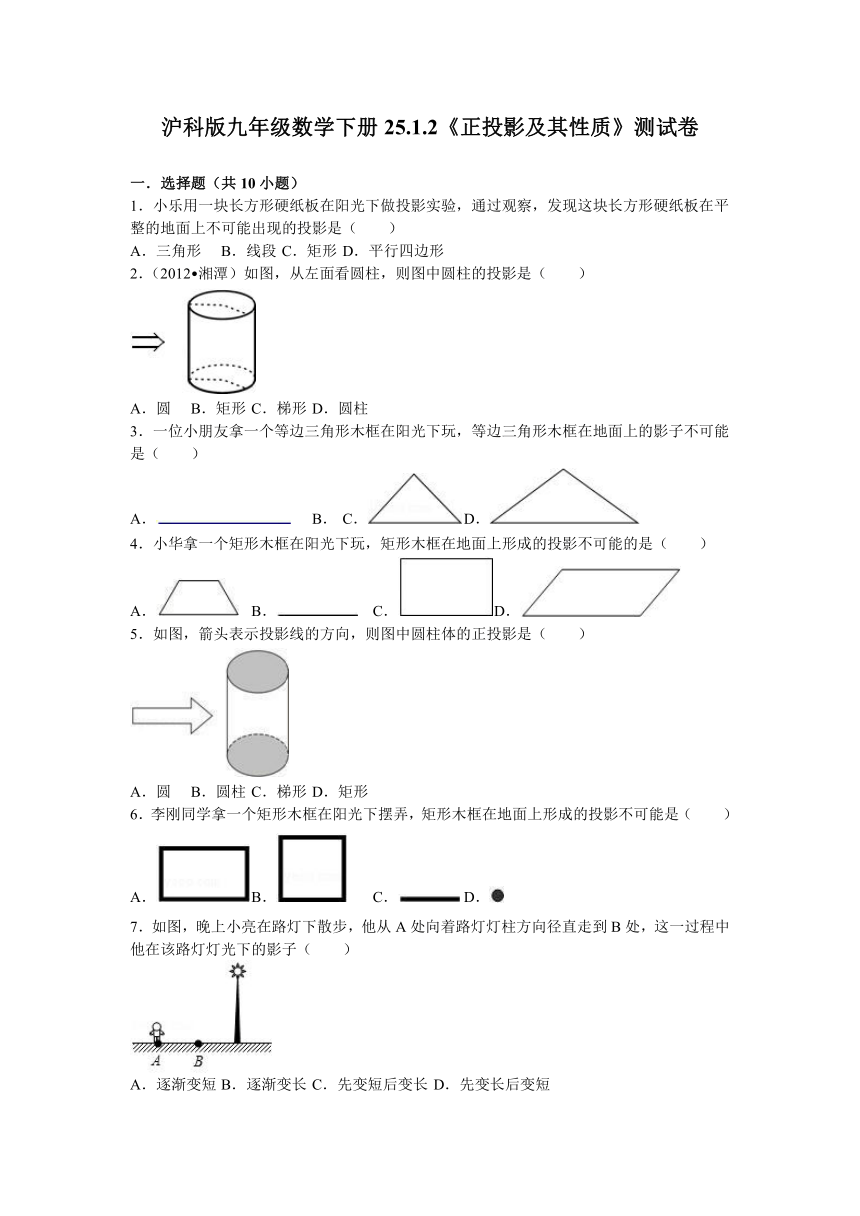 | |
| 格式 | zip | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-07 21:48:27 | ||
图片预览


文档简介
沪科版九年级数学下册25.1.2《正投影及其性质》测试卷
一.选择题(共10小题)
1.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
2.(2012 湘潭)如图,从左面看圆柱,则图中圆柱的投影是( )
A.圆
B.矩形
C.梯形
D.圆柱
3.一位小朋友拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上的影子不可能是( )
A.
B.
C.
D.
4.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能的是( )
A.
B.
C.
D.
5.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆
B.圆柱
C.梯形
D.矩形
6.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是( )
A.
B.
C.
D.
7.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
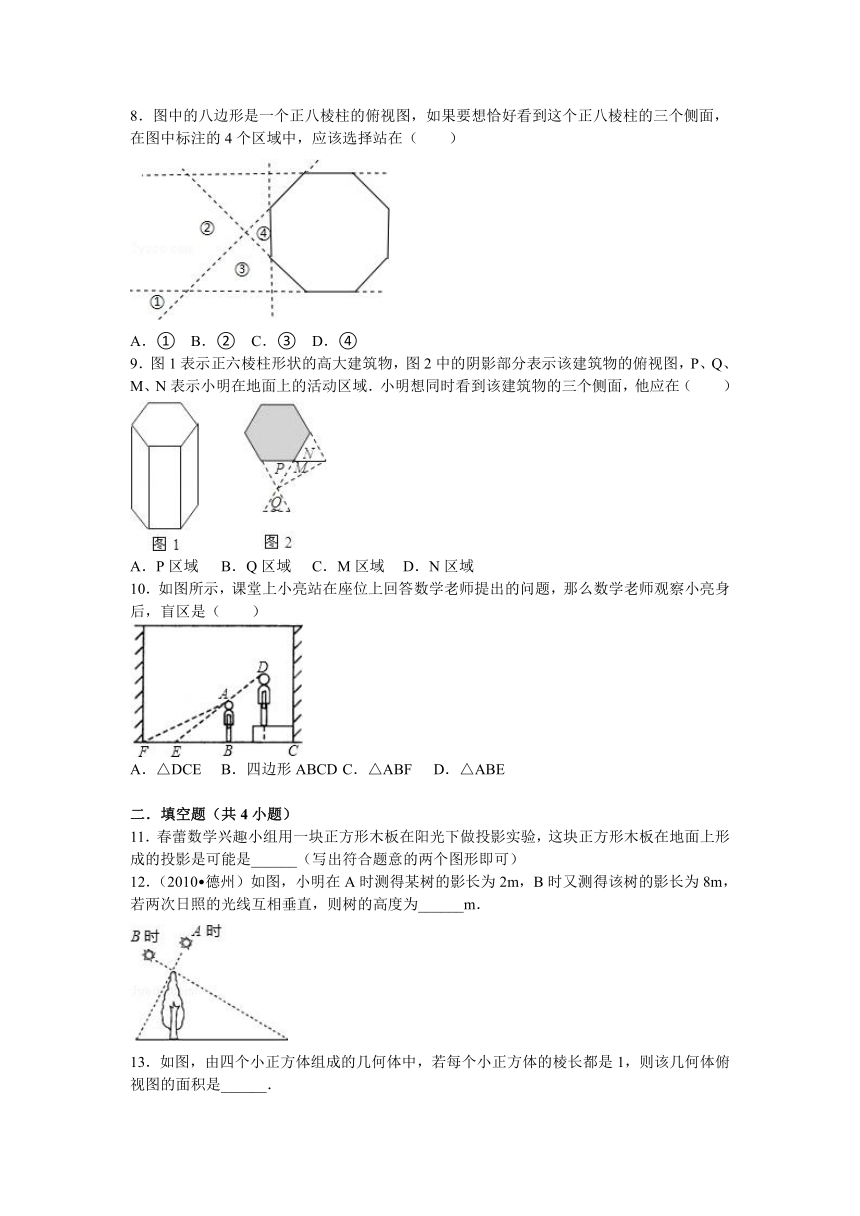
8.图中的八边形是一个正八棱柱的俯视图,如果要想恰好看到这个正八棱柱的三个侧面,在图中标注的4个区域中,应该选择站在( )
A.①
B.②
C.③
D.④
9.图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
A.P区域
B.Q区域
C.M区域
D.N区域
10.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.△DCE
B.四边形ABCD
C.△ABF
D.△ABE
二.填空题(共4小题)
11.春蕾数学兴趣小组用一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影是可能是______(写出符合题意的两个图形即可)
12.(2010 德州)如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为______m.
13.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是______.
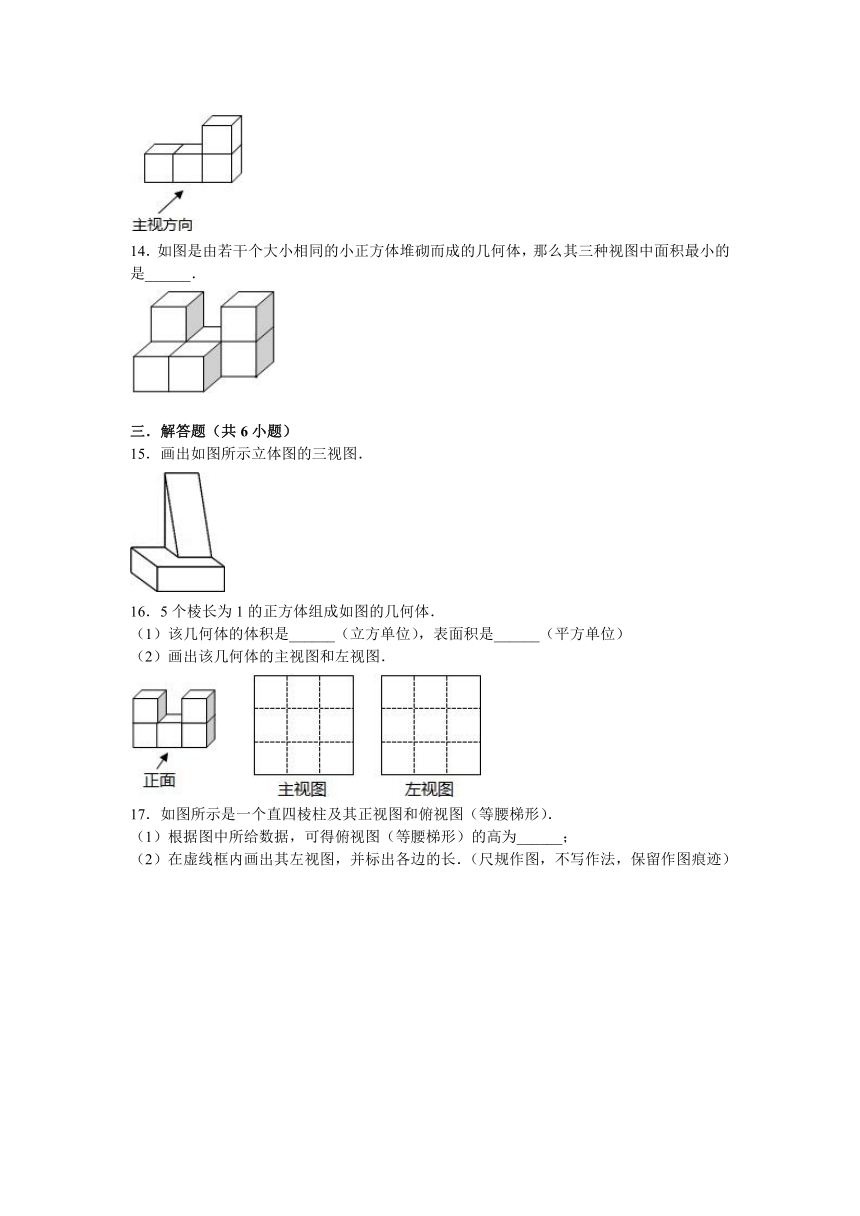
14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______.
三.解答题(共6小题)
15.画出如图所示立体图的三视图.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是______(立方单位),表面积是______(平方单位)
(2)画出该几何体的主视图和左视图.
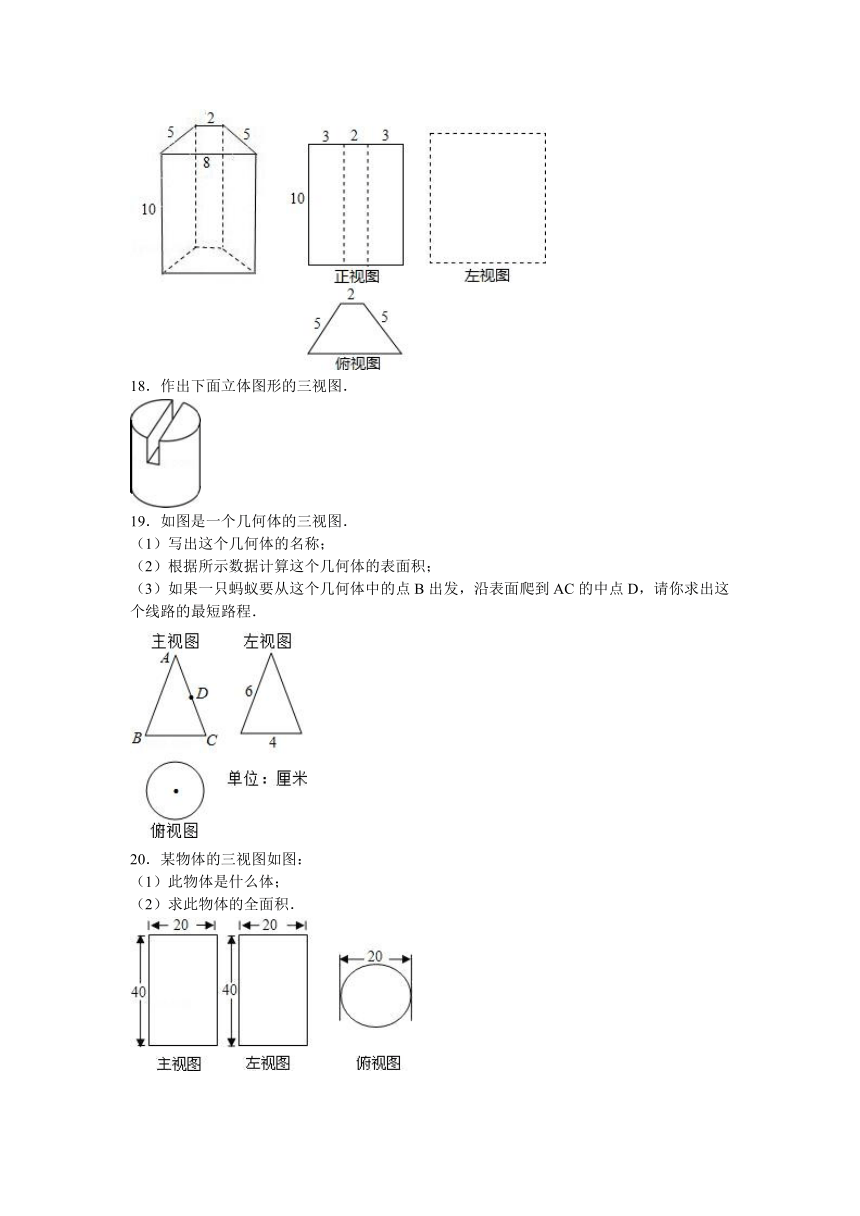
17.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为______;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
18.作出下面立体图形的三视图.
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
20.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
参考答案与试题解析
一.选择题(共10小题)
1.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
【分析】根据平行投影的性质进行分析即可得出答案.
【解答】解:将长方形硬纸的板面与投影线平行时,形成的影子为线段;
将长方形硬纸板与地面平行放置时,形成的影子为矩形;
将长方形硬纸板倾斜放置形成的影子为平行四边形;
由物体同一时刻物高与影长成比例,且长方形对边相等,故得到的投影不可能是三角形.
故选:A.
【点评】本题考查了投影与视图的有关知识,是一道与实际生活密切相关的热点试题,灵活运用平行投影的性质是解题的关键.
2.如图,从左面看圆柱,则图中圆柱的投影是( )
A.圆
B.矩形
C.梯形
D.圆柱
【分析】根据圆柱的左视图的定义直接进行解答即可.
【解答】解:如图所示圆柱从左面看是矩形,
故选:B.
【点评】本题主要考查了简单几何体的三视图,关键是根据三视图的概念得出是解题关键.
3.一位小朋友拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上的影子不可能是( )
A.
B.
C.
D.
【分析】根据看等边三角形木框的方向即可得出答案.
【解答】解:竖直向下看可得到线段,沿与平面平行的方向看可得到C,沿与平面不平行的方向看可得到D,不论如何看都得不到一点.
故选B.
【点评】本题主要考查对平行投影的理解和掌握,能熟练地观察图形得出正确结论是解此题的关键.
4.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能的是( )
A.
B.
C.
D.
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:矩形木框在地面上形成的投影应是平行四边形或一条线段,
即相对的边平行或重合,
故A不可能,即不会是梯形.
故选A.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应视其外在形状,及其与光线的夹角而定.
5.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆
B.圆柱
C.梯形
D.矩形
【分析】根据平行投影特点可知.
【解答】解:根据平行投影特点,图中圆柱体的正投影是矩形.故选D.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应按照物体的外形即光线情况而定.
6.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是( )
A.
B.
C.
D.
【分析】矩形木框在地面上形成的投影应是平行四边形或一条线段,即相对的边平行或重合,故不会是一点,即答案为D.
【解答】解:根据平行投影的特点,矩形木框在地面上行程的投影不可能是一个圆点.故选D.
【点评】本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例,平行物体的影子仍旧平行或重合.
7.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
【分析】由题意易得,小亮离光源是由远到近的过程,根据中心投影的特点,即可得到身影的变化特点.
【解答】解:小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短,
故选:A.
【点评】本题属于基础题,考查了投影的知识,可运用投影的知识或直接联系生活实际解答.
8.图中的八边形是一个正八棱柱的俯视图,如果要想恰好看到这个正八棱柱的三个侧面,在图中标注的4个区域中,应该选择站在( )
A.①
B.②
C.③
D.④
【分析】本题角度比较新颖,从①③④三个角度来看都只能看到正八棱柱的侧面,只有在②的位置上才能看到三个侧面.
【解答】解:①的角度能看到4个侧面;
从③的角度也只能看到两个侧面,
④的角度只能看到一个侧面.
只有②的角度才能看到三个侧面.
故选B.
【点评】本题难度一般,但出题的角度较新颖,现实生活中的问题也是值得注意的.
9.图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
A.P区域
B.Q区域
C.M区域
D.N区域
【分析】根据视点、视角和盲区的定义,观察图形解决.
【解答】解:由图片可知,只有Q区域同时处在三个侧面的观察范围内.
故选:B.
【点评】本题的关键是弄清视点,视角和盲区的定义.
10.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.△DCE
B.四边形ABCD
C.△ABF
D.△ABE
【分析】盲区就是看不到的地区,观察图形可解决.
【解答】解:根据盲区的定义,位于D的视点的盲区应该是三角形ABE的区域.
故选:D.
【点评】此题考查的是视点、视角和盲区,利用数学知识解决实际问题是中学数学的重要内容.本题的关键是弄清盲区的定义.
二.填空题(共4小题)
11.春蕾数学兴趣小组用一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影是可能是 正方形、菱形(答案不唯一) (写出符合题意的两个图形即可)
【分析】平行投影的特点:在同一时刻,平行物体的投影仍旧平行.
【解答】解:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形.
故答案为:正方形、菱形(答案不唯一).
【点评】本题考查了平行投影,太阳光线是平行的,那么对边平行的图形得到的投影依旧平行.
12.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为 4 m.
【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,进而可得=;即DC2=ED FD,代入数据可得答案.
【解答】解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
【点评】本题通过投影的知识结合三角形的相似,求解高的大小;是平行投影性质在实际生活中的应用.
13.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 3 .
【分析】根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
【解答】解:从上面看三个正方形组成的矩形,
矩形的面积为1×3=3.
故答案为:3.
【点评】本题考查了简单组合体的三视图,先确定俯视图,再求面积.
14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 左视图 .
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【解答】解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为:左视图.
【点评】本题考查的是三视图的知识以及学生对该知识点的巩固,难度属简单.解题关键是找到三种视图的正方形的个数.
三.解答题(共6小题)
15.画出如图所示立体图的三视图.
【分析】从正面看下面是一个横着的长方形,上面是一个竖着的长方形;从左面看下面是一个横着的长方形,上面是一个三角形;从上面看是一个大正方形中右上一个小正方形.
【解答】解:如图所示:
【点评】考查了作三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;在画图时一定要将物体的边缘、棱、顶点都体现出来.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 5 (立方单位),表面积是 22 (平方单位)
(2)画出该几何体的主视图和左视图.
【分析】(1)几何体的体积为5个正方体的体积和,表面积为20个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
【解答】解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形(外面4个加里面2个),每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
【点评】考查组合几何体的计算和三视图的画法;用到的知识点为:主视图,左视图分别是从物体的正面和左面看到的平面图形.
17.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为 4 ;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
【分析】(1)过上底的顶点向对边引垂线组成直角三角形求解即可;
(2)易得左视图为长方形,宽等于(1)中算出的梯形的高,高等于正视图图中的10.
【解答】解:(1)4(3分)
作AE⊥BC于点E,则BE=(8﹣2)÷2=3,
∴高AE==4.
(2)
(6分).
【点评】用到的知识点为:求等腰梯形的问题常用辅助线是做等腰梯形的高;左视图反映几何体的宽与高.
18.作出下面立体图形的三视图.
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:
.
【点评】本题考查了几何体的三种视图,掌握定义是关键.注意看得到的棱画实线,看不到的棱画虚线.
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
【分析】考查立体图形的三视图,圆锥的表面积求法及公式的应用.
(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)圆锥的表面积等于扇形的表面积以及圆形的表面积之和;
(3)将圆锥的侧面展开,设顶点为B',连接BB',AC.线段AC与BB'的交点为D,线段BD是最短路程.
【解答】解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)表面积S=S扇形+S圆=+πr2
=πrR+πr2
=12π+4π
=16π(平方厘米),即该几何体全面积为16πcm2;
(3)如图将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.
∵=4π,
∴n=120即∠BAB′=120°.
∵C为弧BB′中点,
∴∠ADB=90°,∠BAD=60°,
∴BD=AB sin∠BAD=6×=cm,
∴路线的最短路程为3√3cm.
【点评】注意把立体图形转化为平面图形的思维,圆锥表面积的计算公式.
20.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
【分析】考查立体图形的三视图,圆柱的全面积的求法及公式的应用.
【解答】解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
【点评】注意立体图形三视图的看法,圆柱的全面积的计算.
一.选择题(共10小题)
1.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
2.(2012 湘潭)如图,从左面看圆柱,则图中圆柱的投影是( )
A.圆
B.矩形
C.梯形
D.圆柱
3.一位小朋友拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上的影子不可能是( )
A.
B.
C.
D.
4.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能的是( )
A.
B.
C.
D.
5.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆
B.圆柱
C.梯形
D.矩形
6.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是( )
A.
B.
C.
D.
7.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
8.图中的八边形是一个正八棱柱的俯视图,如果要想恰好看到这个正八棱柱的三个侧面,在图中标注的4个区域中,应该选择站在( )
A.①
B.②
C.③
D.④
9.图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
A.P区域
B.Q区域
C.M区域
D.N区域
10.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.△DCE
B.四边形ABCD
C.△ABF
D.△ABE
二.填空题(共4小题)
11.春蕾数学兴趣小组用一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影是可能是______(写出符合题意的两个图形即可)
12.(2010 德州)如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为______m.
13.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是______.
14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______.
三.解答题(共6小题)
15.画出如图所示立体图的三视图.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是______(立方单位),表面积是______(平方单位)
(2)画出该几何体的主视图和左视图.
17.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为______;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
18.作出下面立体图形的三视图.
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
20.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
参考答案与试题解析
一.选择题(共10小题)
1.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
【分析】根据平行投影的性质进行分析即可得出答案.
【解答】解:将长方形硬纸的板面与投影线平行时,形成的影子为线段;
将长方形硬纸板与地面平行放置时,形成的影子为矩形;
将长方形硬纸板倾斜放置形成的影子为平行四边形;
由物体同一时刻物高与影长成比例,且长方形对边相等,故得到的投影不可能是三角形.
故选:A.
【点评】本题考查了投影与视图的有关知识,是一道与实际生活密切相关的热点试题,灵活运用平行投影的性质是解题的关键.
2.如图,从左面看圆柱,则图中圆柱的投影是( )
A.圆
B.矩形
C.梯形
D.圆柱
【分析】根据圆柱的左视图的定义直接进行解答即可.
【解答】解:如图所示圆柱从左面看是矩形,
故选:B.
【点评】本题主要考查了简单几何体的三视图,关键是根据三视图的概念得出是解题关键.
3.一位小朋友拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上的影子不可能是( )
A.
B.
C.
D.
【分析】根据看等边三角形木框的方向即可得出答案.
【解答】解:竖直向下看可得到线段,沿与平面平行的方向看可得到C,沿与平面不平行的方向看可得到D,不论如何看都得不到一点.
故选B.
【点评】本题主要考查对平行投影的理解和掌握,能熟练地观察图形得出正确结论是解此题的关键.
4.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能的是( )
A.
B.
C.
D.
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:矩形木框在地面上形成的投影应是平行四边形或一条线段,
即相对的边平行或重合,
故A不可能,即不会是梯形.
故选A.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应视其外在形状,及其与光线的夹角而定.
5.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆
B.圆柱
C.梯形
D.矩形
【分析】根据平行投影特点可知.
【解答】解:根据平行投影特点,图中圆柱体的正投影是矩形.故选D.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应按照物体的外形即光线情况而定.
6.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是( )
A.
B.
C.
D.
【分析】矩形木框在地面上形成的投影应是平行四边形或一条线段,即相对的边平行或重合,故不会是一点,即答案为D.
【解答】解:根据平行投影的特点,矩形木框在地面上行程的投影不可能是一个圆点.故选D.
【点评】本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例,平行物体的影子仍旧平行或重合.
7.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
【分析】由题意易得,小亮离光源是由远到近的过程,根据中心投影的特点,即可得到身影的变化特点.
【解答】解:小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短,
故选:A.
【点评】本题属于基础题,考查了投影的知识,可运用投影的知识或直接联系生活实际解答.
8.图中的八边形是一个正八棱柱的俯视图,如果要想恰好看到这个正八棱柱的三个侧面,在图中标注的4个区域中,应该选择站在( )
A.①
B.②
C.③
D.④
【分析】本题角度比较新颖,从①③④三个角度来看都只能看到正八棱柱的侧面,只有在②的位置上才能看到三个侧面.
【解答】解:①的角度能看到4个侧面;
从③的角度也只能看到两个侧面,
④的角度只能看到一个侧面.
只有②的角度才能看到三个侧面.
故选B.
【点评】本题难度一般,但出题的角度较新颖,现实生活中的问题也是值得注意的.
9.图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
A.P区域
B.Q区域
C.M区域
D.N区域
【分析】根据视点、视角和盲区的定义,观察图形解决.
【解答】解:由图片可知,只有Q区域同时处在三个侧面的观察范围内.
故选:B.
【点评】本题的关键是弄清视点,视角和盲区的定义.
10.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.△DCE
B.四边形ABCD
C.△ABF
D.△ABE
【分析】盲区就是看不到的地区,观察图形可解决.
【解答】解:根据盲区的定义,位于D的视点的盲区应该是三角形ABE的区域.
故选:D.
【点评】此题考查的是视点、视角和盲区,利用数学知识解决实际问题是中学数学的重要内容.本题的关键是弄清盲区的定义.
二.填空题(共4小题)
11.春蕾数学兴趣小组用一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影是可能是 正方形、菱形(答案不唯一) (写出符合题意的两个图形即可)
【分析】平行投影的特点:在同一时刻,平行物体的投影仍旧平行.
【解答】解:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形.
故答案为:正方形、菱形(答案不唯一).
【点评】本题考查了平行投影,太阳光线是平行的,那么对边平行的图形得到的投影依旧平行.
12.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为 4 m.
【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,进而可得=;即DC2=ED FD,代入数据可得答案.
【解答】解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
【点评】本题通过投影的知识结合三角形的相似,求解高的大小;是平行投影性质在实际生活中的应用.
13.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 3 .
【分析】根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
【解答】解:从上面看三个正方形组成的矩形,
矩形的面积为1×3=3.
故答案为:3.
【点评】本题考查了简单组合体的三视图,先确定俯视图,再求面积.
14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 左视图 .
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【解答】解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为:左视图.
【点评】本题考查的是三视图的知识以及学生对该知识点的巩固,难度属简单.解题关键是找到三种视图的正方形的个数.
三.解答题(共6小题)
15.画出如图所示立体图的三视图.
【分析】从正面看下面是一个横着的长方形,上面是一个竖着的长方形;从左面看下面是一个横着的长方形,上面是一个三角形;从上面看是一个大正方形中右上一个小正方形.
【解答】解:如图所示:
【点评】考查了作三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;在画图时一定要将物体的边缘、棱、顶点都体现出来.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 5 (立方单位),表面积是 22 (平方单位)
(2)画出该几何体的主视图和左视图.
【分析】(1)几何体的体积为5个正方体的体积和,表面积为20个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
【解答】解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形(外面4个加里面2个),每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
【点评】考查组合几何体的计算和三视图的画法;用到的知识点为:主视图,左视图分别是从物体的正面和左面看到的平面图形.
17.如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为 4 ;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
【分析】(1)过上底的顶点向对边引垂线组成直角三角形求解即可;
(2)易得左视图为长方形,宽等于(1)中算出的梯形的高,高等于正视图图中的10.
【解答】解:(1)4(3分)
作AE⊥BC于点E,则BE=(8﹣2)÷2=3,
∴高AE==4.
(2)
(6分).
【点评】用到的知识点为:求等腰梯形的问题常用辅助线是做等腰梯形的高;左视图反映几何体的宽与高.
18.作出下面立体图形的三视图.
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:
.
【点评】本题考查了几何体的三种视图,掌握定义是关键.注意看得到的棱画实线,看不到的棱画虚线.
19.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
【分析】考查立体图形的三视图,圆锥的表面积求法及公式的应用.
(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)圆锥的表面积等于扇形的表面积以及圆形的表面积之和;
(3)将圆锥的侧面展开,设顶点为B',连接BB',AC.线段AC与BB'的交点为D,线段BD是最短路程.
【解答】解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)表面积S=S扇形+S圆=+πr2
=πrR+πr2
=12π+4π
=16π(平方厘米),即该几何体全面积为16πcm2;
(3)如图将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.
∵=4π,
∴n=120即∠BAB′=120°.
∵C为弧BB′中点,
∴∠ADB=90°,∠BAD=60°,
∴BD=AB sin∠BAD=6×=cm,
∴路线的最短路程为3√3cm.
【点评】注意把立体图形转化为平面图形的思维,圆锥表面积的计算公式.
20.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
【分析】考查立体图形的三视图,圆柱的全面积的求法及公式的应用.
【解答】解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
【点评】注意立体图形三视图的看法,圆柱的全面积的计算.
