沪科版九年级数学下册24.7.2《圆锥的侧面展开图及计算》测试卷(含答案解析)
文档属性
| 名称 | 沪科版九年级数学下册24.7.2《圆锥的侧面展开图及计算》测试卷(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-07 00:00:00 | ||
图片预览



文档简介
沪科版九年级数学下册24.7.2《圆锥的侧面展开图及计算》
测
试
卷
一.选择题(共10小题)
1.(2016 自贡)圆锥的底面半径为4cm,高为5cm,则它的表面积为( )
A.12πcm2
B.26πcm2
C.πcm2
D.(4+16)πcm2
2.(2016 荆门)如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12cm
B.6cm
C.3cm
D.2cm
3.(2016 贺州)已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2
B.4
C.6
D.8
4.(2016 东营)如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
A.40cm
B.50cm
C.60cm
D.80cm
5.(2016 贵港)如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2,则这个圆锥底面圆的半径是( )
A.
B.
C.
D.
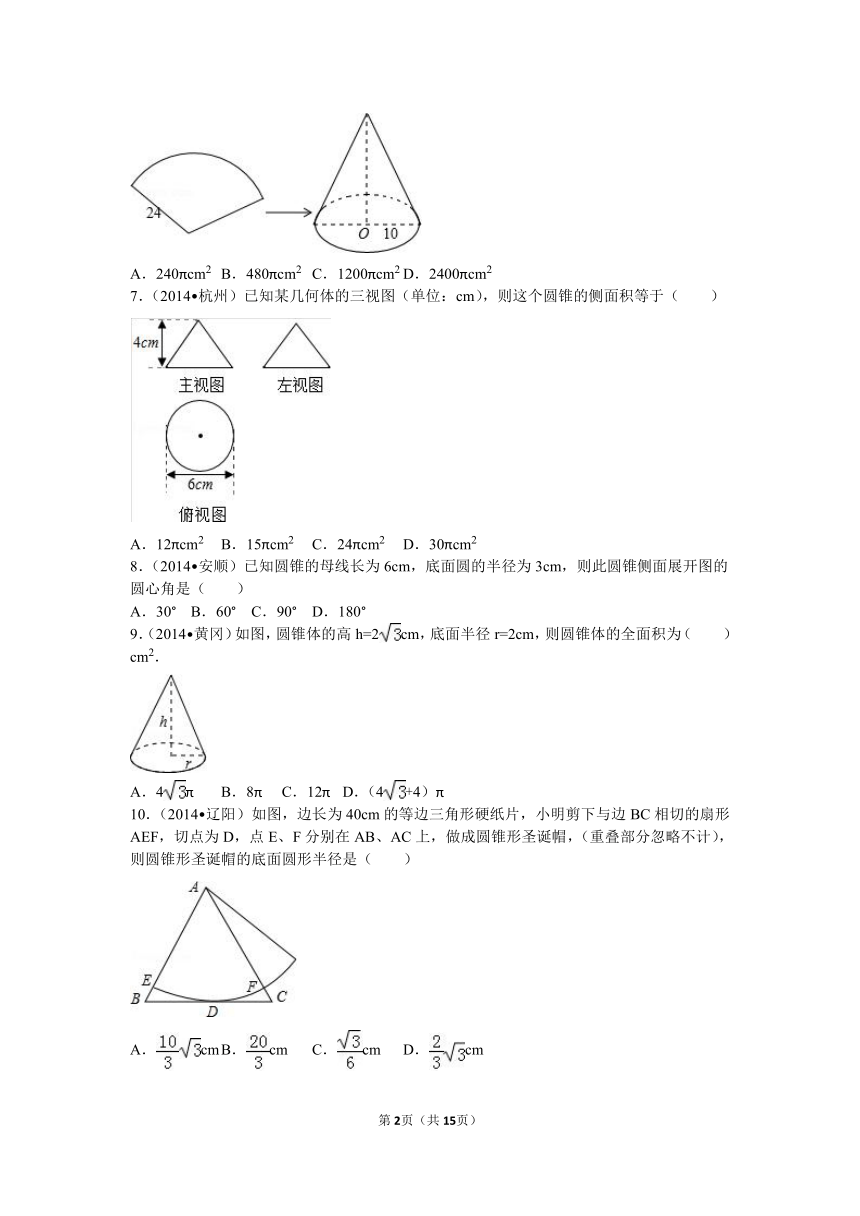
6.(2015 河池)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
A.240πcm2
B.480πcm2
C.1200πcm2
D.2400πcm2
7.(2014 杭州)已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( )
A.12πcm2
B.15πcm2
C.24πcm2
D.30πcm2
8.(2014 安顺)已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°
B.60°
C.90°
D.180°
9.(2014 黄冈)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
A.4π
B.8π
C.12π
D.(4+4)π
10.(2014 辽阳)如图,边长为40cm的等边三角形硬纸片,小明剪下与边BC相切的扇形AEF,切点为D,点E、F分别在AB、AC上,做成圆锥形圣诞帽,(重叠部分忽略不计),则圆锥形圣诞帽的底面圆形半径是( )
A.cm
B.cm
C.cm
D.cm
二.填空题(共4小题)
11.(2016 盐城)已知圆锥的底面半径是2,母线长是4,则圆锥的侧面积是______.
12.(2016 聊城)如图,已知圆锥的高为,高所在直线与母线的夹角为30°,圆锥的侧面积为______.
13.(2016 镇江)圆锥底面圆的半径为4,母线长为5,它的侧面积等于______(结果保留π)
14.(2016 广东)如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是______cm(计算结果保留π).
三.解答题(共6小题)
15.(2013 佛山)如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
16.(2011 杭州)在△ABC中,AB=,AC=,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
17.(2007 荆州)如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子.设BP过底面圆的圆心,已知圆锥体的高为m,底面半径为2m,BE=4m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距水平面的高度.(答案用含根号的式子表示)
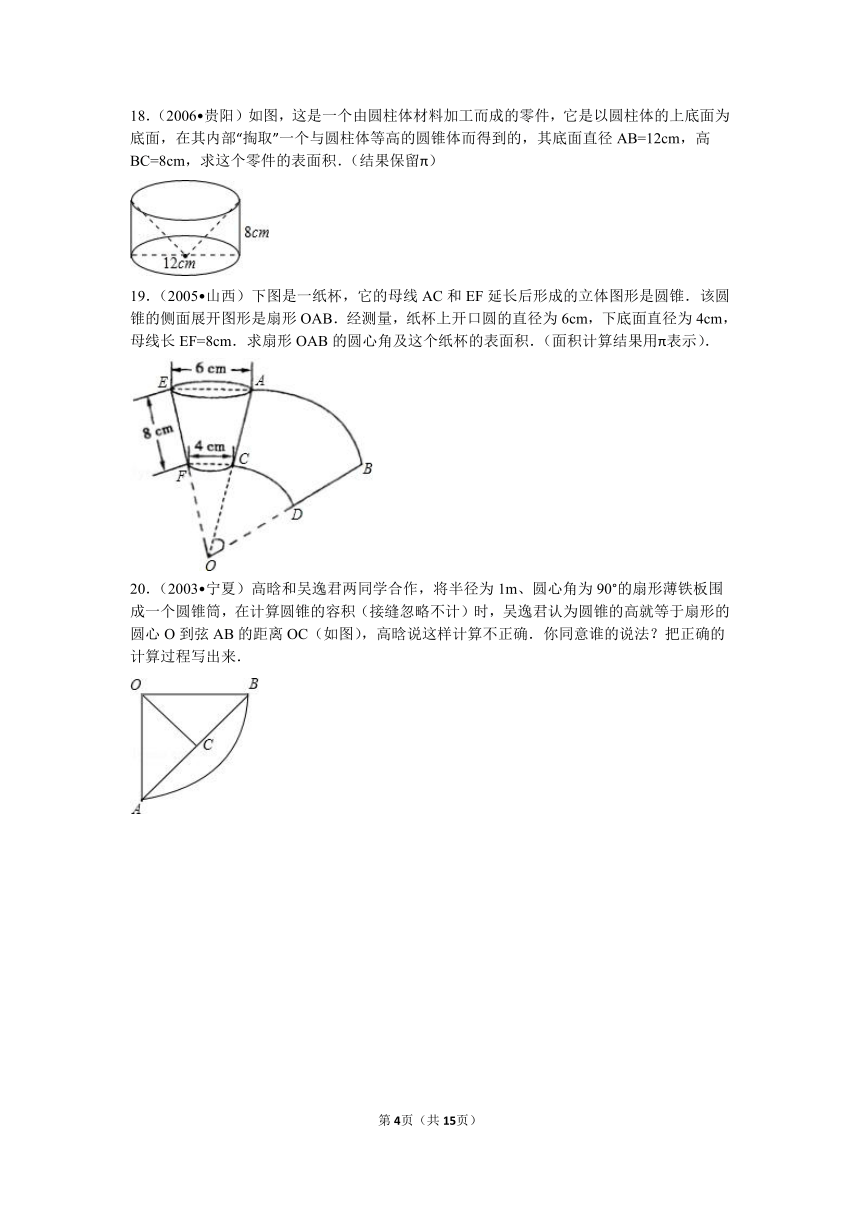
18.(2006 贵阳)如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB=12cm,高BC=8cm,求这个零件的表面积.(结果保留π)
19.(2005 山西)下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
20.(2003 宁夏)高晗和吴逸君两同学合作,将半径为1m、圆心角为90°的扇形薄铁板围成一个圆锥筒,在计算圆锥的容积(接缝忽略不计)时,吴逸君认为圆锥的高就等于扇形的圆心O到弦AB的距离OC(如图),高晗说这样计算不正确.你同意谁的说法?把正确的计算过程写出来.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 自贡)圆锥的底面半径为4cm,高为5cm,则它的表面积为( )
A.12πcm2
B.26πcm2
C.πcm2
D.(4+16)πcm2
【分析】利用勾股定理求得圆锥的母线长,则圆锥表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
【解答】解:底面半径为4cm,则底面周长=8πcm,底面面积=16πcm2;由勾股定理得,母线长=cm,
圆锥的侧面面积=×8π×=4πcm2,∴它的表面积=16π+4π=(4+16)πcm2,故选D.
【点评】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
2.(2016 荆门)如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12cm
B.6cm
C.3cm
D.2cm
【分析】圆的半径为12,求出AB的长度,用弧长公式可求得弧BC的长度,圆锥的底面圆的半径=圆锥的弧长÷2π.
【解答】解:AB===12cm,
∴==6π
∴圆锥的底面圆的半径=6π÷(2π)=3cm.
故选C.
【点评】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
3.(2016 贺州)已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2
B.4
C.6
D.8
【分析】根据圆锥侧面展开图的圆心角与半径(即圆锥的母线的长度)求得的弧长,就是圆锥的底面的周长,然后根据圆的周长公式l=2πr解出r的值即可.
【解答】解:设圆锥的底面半径为r.
圆锥的侧面展开扇形的半径为12,
∵它的侧面展开图的圆心角是120°,
∴弧长==8π,
即圆锥底面的周长是8π,
∴8π=2πr,解得,r=4,
∴底面圆的直径为8.
故选D.
【点评】本题考查了圆锥的计算.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
4.(2016 东营)如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
A.40cm
B.50cm
C.60cm
D.80cm
【分析】首先根据圆锥的底面直径求得圆锥的底面周长,然后根据底面周长等于展开扇形的弧长求得铁皮的半径即可.
【解答】解:∵圆锥的底面直径为60cm,
∴圆锥的底面周长为60πcm,
∴扇形的弧长为60πcm,
设扇形的半径为r,
则=60π,
解得:r=40cm,
故选A.
【点评】本题考查了圆锥的计算,解题的关键是首先求得圆锥的底面周长,利用圆锥的底面周长等于扇形的弧长求解.
5.(2016 贵港)如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2,则这个圆锥底面圆的半径是( )
A.
B.
C.
D.
【分析】根据扇形的圆心角的度数和直径BC的长确定扇形的半径,然后确定扇形的弧长,根据圆锥的底面周长等于扇形的弧长列式求解即可.
【解答】解:如图,连接AO,∠BAC=120°,
∵BC=2,∠OAC=60°,
∴OC=,
∴AC=2,
设圆锥的底面半径为r,则2πr==π,
解得:r=,
故选B.
【点评】本题考查了圆锥的计算,解题的关键是能够了解圆锥的底面周长等于展开扇形的弧长,难度不大.
6.(2015 河池)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
A.240πcm2
B.480πcm2
C.1200πcm2
D.2400πcm2
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算即可.
【解答】解:这张扇形纸板的面积=×2π×10×24=240π(cm2).
故选A.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
7.(2014 杭州)已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( )
A.12πcm2
B.15πcm2
C.24πcm2
D.30πcm2
【分析】俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.
【解答】解:∵底面半径为3,高为4,
∴圆锥母线长为5,
∴侧面积=2πrR÷2=15πcm2.
故选:B.
【点评】由该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.
8.(2014 安顺)已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°
B.60°
C.90°
D.180°
【分析】根据弧长=圆锥底面周长=6π,圆心角=弧长×180÷母线长÷π计算.
【解答】解:由题意知:弧长=圆锥底面周长=2×3π=6πcm,
扇形的圆心角=弧长×180÷母线长÷π=6π×180÷6π=180°.
故选:D.
【点评】本题考查的知识点为:弧长=圆锥底面周长及弧长与圆心角的关系.解题的关键是熟知圆锥与扇形的相关元素的对应关系.
9.(2014 黄冈)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
A.4π
B.8π
C.12π
D.(4+4)π
【分析】表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
【解答】解:底面圆的半径为2,则底面周长=4π,
∵底面半径为2cm、高为2cm,
∴圆锥的母线长为4cm,
∴侧面面积=×4π×4=8π;
底面积为=4π,
全面积为:8π+4π=12πcm2.
故选:C.
【点评】本题利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.
10.(2014 辽阳)如图,边长为40cm的等边三角形硬纸片,小明剪下与边BC相切的扇形AEF,切点为D,点E、F分别在AB、AC上,做成圆锥形圣诞帽,(重叠部分忽略不计),则圆锥形圣诞帽的底面圆形半径是( )
A.cm
B.cm
C.cm
D.cm
【分析】连结AD,如图,根据切线的性质得AD⊥BC,再根据等边三角形的性质得∠BAC=∠B=60°,BD=BC=20,所以AD=BD=20,设圆锥形圣诞帽的底面圆形半径为rcm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,再解方程即可.
【解答】解:连结AD,如图,
∵边BC相切于扇形AEF,切点为D,
∴AD⊥BC,
∵△ABC为等边三角形,
∴∠BAC=∠B=60°,BD=BC=×40=20,
∴AD=BD=20,
设圆锥形圣诞帽的底面圆形半径为rcm,
∴2πr=,解得r=(cm),
即圆锥形圣诞帽的底面圆形半径为cm.
故选A.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
二.填空题(共4小题)
11.(2016 盐城)已知圆锥的底面半径是2,母线长是4,则圆锥的侧面积是 8π .
【分析】圆锥的侧面积=底面周长×母线长÷2.
【解答】解:底面半径是2,则底面周长=4π,圆锥的侧面积=×4π×4=8π.
【点评】本题利用了圆的周长公式和扇形面积公式求解.
12.(2016 聊城)如图,已知圆锥的高为,高所在直线与母线的夹角为30°,圆锥的侧面积为 2π .
【分析】先利用三角函数计算出BO,再利用勾股定理计算出AB,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算圆锥的侧面积.
【解答】解:如图,∠BAO=30°,AO=,
在Rt△ABO中,∵tan∠BAO=,
∴BO=tan30°=1,即圆锥的底面圆的半径为1,
∴AB==2,即圆锥的母线长为2,
∴圆锥的侧面积= 2π 1 2=2π.
故答案为2π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
13.(2016 镇江)圆锥底面圆的半径为4,母线长为5,它的侧面积等于 20π (结果保留π)
【分析】根据圆锥的底面半径为4,母线长为5,直接利用圆锥的侧面积公式求出它的侧面积.
【解答】解:根据圆锥的侧面积公式:πrl=π×4×5=20π,
故答案为:20π.
【点评】此题主要考查了圆锥侧面积公式.掌握圆锥侧面积公式:S侧=πrl是解决问题的关键.
14.(2016 广东)如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是 10π cm(计算结果保留π).
【分析】根据的长就是圆锥的底面周长即可求解.
【解答】解:∵圆锥的高h为12cm,OA=13cm,
∴圆锥的底面半径为=5cm,
∴圆锥的底面周长为10πcm,
∴扇形AOC中的长是10πcm,
故答案为:10π.
【点评】本题考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于展开扇形的弧长,难度不大.
三.解答题(共6小题)
15.(2013 佛山)如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
【分析】设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.
【解答】解:设圆锥的母线长为l,底面半径为r,
则:πl=2πr,
∴l=2r,
∴母线与高的夹角的正弦值==,
∴母线AB与高AO的夹角30°.
【点评】此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.
16.(2011 杭州)在△ABC中,AB=,AC=,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
【分析】(1)根据勾股定理的逆定理得到△ABC是直角三角形,且∠C=90°,利用三角函数计算出sinA,然后与sin30°进行比较即可判断∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,圆锥的底面圆的半径为AC,母线长为AB,所得几何体的表面积分为底面积和侧面积,分别根据圆的面积公式和扇形的面积公式进行计算即可.
【解答】证明:(1)∵BC2+AC2=1+2=3=AB2,
∴△ABC是直角三角形,且∠C=90°.
∵,
∴∠A≠30°.
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴圆锥的底面圆的半径=,
∴圆锥的底面圆的周长=2π =2π;母线长为,
∴几何体的表面积π+π×()2=π+2π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,它的弧长为圆锥的底面圆的周长,扇形的半径为母线长,圆锥的侧面积=扇形的面积=l R(l为弧长,R为扇形的半径);也考查了勾股定理的逆定理以及特殊角的三角函数值.
17.(2007 荆州)如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子.设BP过底面圆的圆心,已知圆锥体的高为m,底面半径为2m,BE=4m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距水平面的高度.(答案用含根号的式子表示)
【分析】(1)易得OB长,那么可求得∠B的正切值,就可求得∠B的度数;
(2)根据所给条件可得AC为BC长度,利用相应的三角函数可求得光源A距水平面的高度.
【解答】解:(1)如图,圆锥的高DO=.
在Rt△DOB中,OB=BE+EO=4+2=6,
∴tan∠B=,
∴∠B=30°;
(2)过点A作AF⊥BP,垂足为F.
∵∠B=30°,
∴∠ACP=2∠B=60°.
又∠ACP=∠B+∠BAC,
∴∠B=∠BAC,
∴AC=BC=BE+EC=8,
在Rt△ACF中,AF=ACsin∠ACF=8sin60°=4.
答:灯源离地面的高度为4米.
【点评】本题通过构造直角三角形,利用锐角三角函数的概念,直角三角形的性质,等角对等边求解.
18.(2006 贵阳)如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB=12cm,高BC=8cm,求这个零件的表面积.(结果保留π)
【分析】这个零件的表面积分为三部分:锥形的侧面面积,圆柱的侧面面积,圆柱的底面面积.分别求得相加即可.
【解答】解:这个零件的底面积=;
这个零件的圆柱的侧面积=12π 8=96π;
圆锥母线长,
这个零件的内侧面积=;
∴这个零件的表面积为:36π+96π+60π=192πcm2.
【点评】用到的知识点为:圆锥的侧面积=底面周长×母线长÷2;圆柱侧面积=底面周长×高;圆锥底面积=π×半径2.
19.(2005 山西)下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
【分析】(1)设∠AOB=n°,AO=R,则CO=R﹣8,利用圆锥的侧面展开图扇形的弧长等于圆锥底面周长作为相等关系列方程,并联立成方程组求解即可;
(2)求纸杯的侧面积即为扇环的面积,需要用大扇形的面积减去小扇形的面积.纸杯表面积=S纸杯侧面积+S纸杯底面积.
【解答】解:由题意可知:=6π,=4π,设∠AOB=n,AO=R,则CO=R﹣8,
由弧长公式得:=4π,
∴,
解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R﹣8=16,
∴S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=72π﹣32π=40π(cm2),
纸杯底面积=π 22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).
【点评】主要考查圆锥的侧面展开图与底面周长之间的关系和扇环的面积的求法.
本题中(1)就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解;
(2)扇环的面积等于大扇形的面积减去小扇形的面积.
20.(2003 宁夏)高晗和吴逸君两同学合作,将半径为1m、圆心角为90°的扇形薄铁板围成一个圆锥筒,在计算圆锥的容积(接缝忽略不计)时,吴逸君认为圆锥的高就等于扇形的圆心O到弦AB的距离OC(如图),高晗说这样计算不正确.你同意谁的说法?把正确的计算过程写出来.
【分析】易得OC的长度;圆锥的高,母线长,底面半径组成直角三角形,母线长为1,根据底面周长等于弧长可得到底面半径,进而利用勾股定理求得圆锥高,和吴逸君说的比较即可.
【解答】解:如图1,
在Rt△OAC中,
OC=OAsin∠OAC=OA sin45°=;
如图2,
在Rt△OO′A中,
OA=1,底面周长=O′A×2π=的长=2π×,
∴O′A=
由勾股定理知,OO′===,
∵,
∴吴逸君的说法不正确.
【点评】本题利用了等腰直角三角形的性质,勾股定理,圆的周长公式,弧长公式求解.
第1页(共1页)
测
试
卷
一.选择题(共10小题)
1.(2016 自贡)圆锥的底面半径为4cm,高为5cm,则它的表面积为( )
A.12πcm2
B.26πcm2
C.πcm2
D.(4+16)πcm2
2.(2016 荆门)如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12cm
B.6cm
C.3cm
D.2cm
3.(2016 贺州)已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2
B.4
C.6
D.8
4.(2016 东营)如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
A.40cm
B.50cm
C.60cm
D.80cm
5.(2016 贵港)如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2,则这个圆锥底面圆的半径是( )
A.
B.
C.
D.
6.(2015 河池)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
A.240πcm2
B.480πcm2
C.1200πcm2
D.2400πcm2
7.(2014 杭州)已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( )
A.12πcm2
B.15πcm2
C.24πcm2
D.30πcm2
8.(2014 安顺)已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°
B.60°
C.90°
D.180°
9.(2014 黄冈)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
A.4π
B.8π
C.12π
D.(4+4)π
10.(2014 辽阳)如图,边长为40cm的等边三角形硬纸片,小明剪下与边BC相切的扇形AEF,切点为D,点E、F分别在AB、AC上,做成圆锥形圣诞帽,(重叠部分忽略不计),则圆锥形圣诞帽的底面圆形半径是( )
A.cm
B.cm
C.cm
D.cm
二.填空题(共4小题)
11.(2016 盐城)已知圆锥的底面半径是2,母线长是4,则圆锥的侧面积是______.
12.(2016 聊城)如图,已知圆锥的高为,高所在直线与母线的夹角为30°,圆锥的侧面积为______.
13.(2016 镇江)圆锥底面圆的半径为4,母线长为5,它的侧面积等于______(结果保留π)
14.(2016 广东)如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是______cm(计算结果保留π).
三.解答题(共6小题)
15.(2013 佛山)如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
16.(2011 杭州)在△ABC中,AB=,AC=,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
17.(2007 荆州)如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子.设BP过底面圆的圆心,已知圆锥体的高为m,底面半径为2m,BE=4m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距水平面的高度.(答案用含根号的式子表示)
18.(2006 贵阳)如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB=12cm,高BC=8cm,求这个零件的表面积.(结果保留π)
19.(2005 山西)下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
20.(2003 宁夏)高晗和吴逸君两同学合作,将半径为1m、圆心角为90°的扇形薄铁板围成一个圆锥筒,在计算圆锥的容积(接缝忽略不计)时,吴逸君认为圆锥的高就等于扇形的圆心O到弦AB的距离OC(如图),高晗说这样计算不正确.你同意谁的说法?把正确的计算过程写出来.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 自贡)圆锥的底面半径为4cm,高为5cm,则它的表面积为( )
A.12πcm2
B.26πcm2
C.πcm2
D.(4+16)πcm2
【分析】利用勾股定理求得圆锥的母线长,则圆锥表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
【解答】解:底面半径为4cm,则底面周长=8πcm,底面面积=16πcm2;由勾股定理得,母线长=cm,
圆锥的侧面面积=×8π×=4πcm2,∴它的表面积=16π+4π=(4+16)πcm2,故选D.
【点评】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
2.(2016 荆门)如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.12cm
B.6cm
C.3cm
D.2cm
【分析】圆的半径为12,求出AB的长度,用弧长公式可求得弧BC的长度,圆锥的底面圆的半径=圆锥的弧长÷2π.
【解答】解:AB===12cm,
∴==6π
∴圆锥的底面圆的半径=6π÷(2π)=3cm.
故选C.
【点评】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
3.(2016 贺州)已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A.2
B.4
C.6
D.8
【分析】根据圆锥侧面展开图的圆心角与半径(即圆锥的母线的长度)求得的弧长,就是圆锥的底面的周长,然后根据圆的周长公式l=2πr解出r的值即可.
【解答】解:设圆锥的底面半径为r.
圆锥的侧面展开扇形的半径为12,
∵它的侧面展开图的圆心角是120°,
∴弧长==8π,
即圆锥底面的周长是8π,
∴8π=2πr,解得,r=4,
∴底面圆的直径为8.
故选D.
【点评】本题考查了圆锥的计算.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
4.(2016 东营)如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
A.40cm
B.50cm
C.60cm
D.80cm
【分析】首先根据圆锥的底面直径求得圆锥的底面周长,然后根据底面周长等于展开扇形的弧长求得铁皮的半径即可.
【解答】解:∵圆锥的底面直径为60cm,
∴圆锥的底面周长为60πcm,
∴扇形的弧长为60πcm,
设扇形的半径为r,
则=60π,
解得:r=40cm,
故选A.
【点评】本题考查了圆锥的计算,解题的关键是首先求得圆锥的底面周长,利用圆锥的底面周长等于扇形的弧长求解.
5.(2016 贵港)如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2,则这个圆锥底面圆的半径是( )
A.
B.
C.
D.
【分析】根据扇形的圆心角的度数和直径BC的长确定扇形的半径,然后确定扇形的弧长,根据圆锥的底面周长等于扇形的弧长列式求解即可.
【解答】解:如图,连接AO,∠BAC=120°,
∵BC=2,∠OAC=60°,
∴OC=,
∴AC=2,
设圆锥的底面半径为r,则2πr==π,
解得:r=,
故选B.
【点评】本题考查了圆锥的计算,解题的关键是能够了解圆锥的底面周长等于展开扇形的弧长,难度不大.
6.(2015 河池)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
A.240πcm2
B.480πcm2
C.1200πcm2
D.2400πcm2
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算即可.
【解答】解:这张扇形纸板的面积=×2π×10×24=240π(cm2).
故选A.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
7.(2014 杭州)已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( )
A.12πcm2
B.15πcm2
C.24πcm2
D.30πcm2
【分析】俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.
【解答】解:∵底面半径为3,高为4,
∴圆锥母线长为5,
∴侧面积=2πrR÷2=15πcm2.
故选:B.
【点评】由该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.
8.(2014 安顺)已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°
B.60°
C.90°
D.180°
【分析】根据弧长=圆锥底面周长=6π,圆心角=弧长×180÷母线长÷π计算.
【解答】解:由题意知:弧长=圆锥底面周长=2×3π=6πcm,
扇形的圆心角=弧长×180÷母线长÷π=6π×180÷6π=180°.
故选:D.
【点评】本题考查的知识点为:弧长=圆锥底面周长及弧长与圆心角的关系.解题的关键是熟知圆锥与扇形的相关元素的对应关系.
9.(2014 黄冈)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
A.4π
B.8π
C.12π
D.(4+4)π
【分析】表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
【解答】解:底面圆的半径为2,则底面周长=4π,
∵底面半径为2cm、高为2cm,
∴圆锥的母线长为4cm,
∴侧面面积=×4π×4=8π;
底面积为=4π,
全面积为:8π+4π=12πcm2.
故选:C.
【点评】本题利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.
10.(2014 辽阳)如图,边长为40cm的等边三角形硬纸片,小明剪下与边BC相切的扇形AEF,切点为D,点E、F分别在AB、AC上,做成圆锥形圣诞帽,(重叠部分忽略不计),则圆锥形圣诞帽的底面圆形半径是( )
A.cm
B.cm
C.cm
D.cm
【分析】连结AD,如图,根据切线的性质得AD⊥BC,再根据等边三角形的性质得∠BAC=∠B=60°,BD=BC=20,所以AD=BD=20,设圆锥形圣诞帽的底面圆形半径为rcm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,再解方程即可.
【解答】解:连结AD,如图,
∵边BC相切于扇形AEF,切点为D,
∴AD⊥BC,
∵△ABC为等边三角形,
∴∠BAC=∠B=60°,BD=BC=×40=20,
∴AD=BD=20,
设圆锥形圣诞帽的底面圆形半径为rcm,
∴2πr=,解得r=(cm),
即圆锥形圣诞帽的底面圆形半径为cm.
故选A.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
二.填空题(共4小题)
11.(2016 盐城)已知圆锥的底面半径是2,母线长是4,则圆锥的侧面积是 8π .
【分析】圆锥的侧面积=底面周长×母线长÷2.
【解答】解:底面半径是2,则底面周长=4π,圆锥的侧面积=×4π×4=8π.
【点评】本题利用了圆的周长公式和扇形面积公式求解.
12.(2016 聊城)如图,已知圆锥的高为,高所在直线与母线的夹角为30°,圆锥的侧面积为 2π .
【分析】先利用三角函数计算出BO,再利用勾股定理计算出AB,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算圆锥的侧面积.
【解答】解:如图,∠BAO=30°,AO=,
在Rt△ABO中,∵tan∠BAO=,
∴BO=tan30°=1,即圆锥的底面圆的半径为1,
∴AB==2,即圆锥的母线长为2,
∴圆锥的侧面积= 2π 1 2=2π.
故答案为2π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
13.(2016 镇江)圆锥底面圆的半径为4,母线长为5,它的侧面积等于 20π (结果保留π)
【分析】根据圆锥的底面半径为4,母线长为5,直接利用圆锥的侧面积公式求出它的侧面积.
【解答】解:根据圆锥的侧面积公式:πrl=π×4×5=20π,
故答案为:20π.
【点评】此题主要考查了圆锥侧面积公式.掌握圆锥侧面积公式:S侧=πrl是解决问题的关键.
14.(2016 广东)如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是 10π cm(计算结果保留π).
【分析】根据的长就是圆锥的底面周长即可求解.
【解答】解:∵圆锥的高h为12cm,OA=13cm,
∴圆锥的底面半径为=5cm,
∴圆锥的底面周长为10πcm,
∴扇形AOC中的长是10πcm,
故答案为:10π.
【点评】本题考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于展开扇形的弧长,难度不大.
三.解答题(共6小题)
15.(2013 佛山)如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
【分析】设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.
【解答】解:设圆锥的母线长为l,底面半径为r,
则:πl=2πr,
∴l=2r,
∴母线与高的夹角的正弦值==,
∴母线AB与高AO的夹角30°.
【点评】此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.
16.(2011 杭州)在△ABC中,AB=,AC=,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
【分析】(1)根据勾股定理的逆定理得到△ABC是直角三角形,且∠C=90°,利用三角函数计算出sinA,然后与sin30°进行比较即可判断∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,圆锥的底面圆的半径为AC,母线长为AB,所得几何体的表面积分为底面积和侧面积,分别根据圆的面积公式和扇形的面积公式进行计算即可.
【解答】证明:(1)∵BC2+AC2=1+2=3=AB2,
∴△ABC是直角三角形,且∠C=90°.
∵,
∴∠A≠30°.
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴圆锥的底面圆的半径=,
∴圆锥的底面圆的周长=2π =2π;母线长为,
∴几何体的表面积π+π×()2=π+2π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,它的弧长为圆锥的底面圆的周长,扇形的半径为母线长,圆锥的侧面积=扇形的面积=l R(l为弧长,R为扇形的半径);也考查了勾股定理的逆定理以及特殊角的三角函数值.
17.(2007 荆州)如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子.设BP过底面圆的圆心,已知圆锥体的高为m,底面半径为2m,BE=4m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距水平面的高度.(答案用含根号的式子表示)
【分析】(1)易得OB长,那么可求得∠B的正切值,就可求得∠B的度数;
(2)根据所给条件可得AC为BC长度,利用相应的三角函数可求得光源A距水平面的高度.
【解答】解:(1)如图,圆锥的高DO=.
在Rt△DOB中,OB=BE+EO=4+2=6,
∴tan∠B=,
∴∠B=30°;
(2)过点A作AF⊥BP,垂足为F.
∵∠B=30°,
∴∠ACP=2∠B=60°.
又∠ACP=∠B+∠BAC,
∴∠B=∠BAC,
∴AC=BC=BE+EC=8,
在Rt△ACF中,AF=ACsin∠ACF=8sin60°=4.
答:灯源离地面的高度为4米.
【点评】本题通过构造直角三角形,利用锐角三角函数的概念,直角三角形的性质,等角对等边求解.
18.(2006 贵阳)如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB=12cm,高BC=8cm,求这个零件的表面积.(结果保留π)
【分析】这个零件的表面积分为三部分:锥形的侧面面积,圆柱的侧面面积,圆柱的底面面积.分别求得相加即可.
【解答】解:这个零件的底面积=;
这个零件的圆柱的侧面积=12π 8=96π;
圆锥母线长,
这个零件的内侧面积=;
∴这个零件的表面积为:36π+96π+60π=192πcm2.
【点评】用到的知识点为:圆锥的侧面积=底面周长×母线长÷2;圆柱侧面积=底面周长×高;圆锥底面积=π×半径2.
19.(2005 山西)下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
【分析】(1)设∠AOB=n°,AO=R,则CO=R﹣8,利用圆锥的侧面展开图扇形的弧长等于圆锥底面周长作为相等关系列方程,并联立成方程组求解即可;
(2)求纸杯的侧面积即为扇环的面积,需要用大扇形的面积减去小扇形的面积.纸杯表面积=S纸杯侧面积+S纸杯底面积.
【解答】解:由题意可知:=6π,=4π,设∠AOB=n,AO=R,则CO=R﹣8,
由弧长公式得:=4π,
∴,
解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R﹣8=16,
∴S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=72π﹣32π=40π(cm2),
纸杯底面积=π 22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).
【点评】主要考查圆锥的侧面展开图与底面周长之间的关系和扇环的面积的求法.
本题中(1)就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解;
(2)扇环的面积等于大扇形的面积减去小扇形的面积.
20.(2003 宁夏)高晗和吴逸君两同学合作,将半径为1m、圆心角为90°的扇形薄铁板围成一个圆锥筒,在计算圆锥的容积(接缝忽略不计)时,吴逸君认为圆锥的高就等于扇形的圆心O到弦AB的距离OC(如图),高晗说这样计算不正确.你同意谁的说法?把正确的计算过程写出来.
【分析】易得OC的长度;圆锥的高,母线长,底面半径组成直角三角形,母线长为1,根据底面周长等于弧长可得到底面半径,进而利用勾股定理求得圆锥高,和吴逸君说的比较即可.
【解答】解:如图1,
在Rt△OAC中,
OC=OAsin∠OAC=OA sin45°=;
如图2,
在Rt△OO′A中,
OA=1,底面周长=O′A×2π=的长=2π×,
∴O′A=
由勾股定理知,OO′===,
∵,
∴吴逸君的说法不正确.
【点评】本题利用了等腰直角三角形的性质,勾股定理,圆的周长公式,弧长公式求解.
第1页(共1页)
