沪科版九年级数学下册24.4.2《切线的判定与性质》测试卷(含答案解析)
文档属性
| 名称 | 沪科版九年级数学下册24.4.2《切线的判定与性质》测试卷(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 434.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-07 00:00:00 | ||
图片预览




文档简介
沪科版九年级数学下册24.4.2《切线的判定与性质》测试卷
一.选择题(共10小题)
1.(2015 滦平县二模)如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4
B.8
C.4或6
D.4或8
2.(2015 湖北模拟)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
3.(2015 蒙城县校级模拟)如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE=EC,则AC是⊙O的切线
4.(2014 泰安)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
5.(2012 桂平市三模)如图,直线AC∥BD,⊙O与AC和BD分别相切于点A和点B.点M和点N分别是AC和BD上的动点,MN沿AC和BD平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.直线AC和BD的距离为2
B.若∠MON=90°,则MN与⊙O相切
C.若MN与⊙O相切,则AM=
D.MN=
6.(2012秋 汉阳区期中)如图,在梯形ABCD中,AB∥DC.
①若∠A=90°,AB+CD=BC,则以AD为直径的圆与BC相切;
②若∠A=90°,当以AD为直径的圆与BC相切,则以BC为直径的圆也与AD相切;
③若以AD为直径的圆与BC相切,则AB+CD=BC;
④若以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.
以上判断正确的个数有( )
A.1
B.2
C.3
D.4
7.(2009秋 常熟市期末)如图,线段AB是⊙O的直径,⊙O交线段BC于D,且D是BC中点,DE⊥AC于E,连接AD,则下列结论正确的个数是( )
①CE CA=CD CB;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线;⑤AD2=AE AB.
A.2个
B.3个
C.4个
D.5个
8.(2007 上海校级模拟)下列命题中,假命题是( )
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
9.(2016 厦门校级二模)如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
①l1和l2的距离为2
②MN=
③当直线MN与⊙O相切时,∠MON=90°
④当AM+BN=时,直线MN与⊙O相切.正确的个数是( )
A.1
B.2
C.3
D.4
10.(2009 硚口区一模)已知⊙O是△ABC的外接圆,⊙O半径为R,AD是△ABC的高,E是
的中点,EF与⊙O切于E,交AC的延长线于F,则下列结论:
①AC AB=2R AD;
②EF∥BC;
③CF AC=EF CM;
④.
其中正确的结论是( )
A.①②③
B.①③④
C.②③④
D.①②③④
二.填空题(共4小题)
11.(2015 哈尔滨模拟)如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=,BD=2,则线段AE的长为______.
12.(2015 河南模拟)如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=,则PA的长为______.
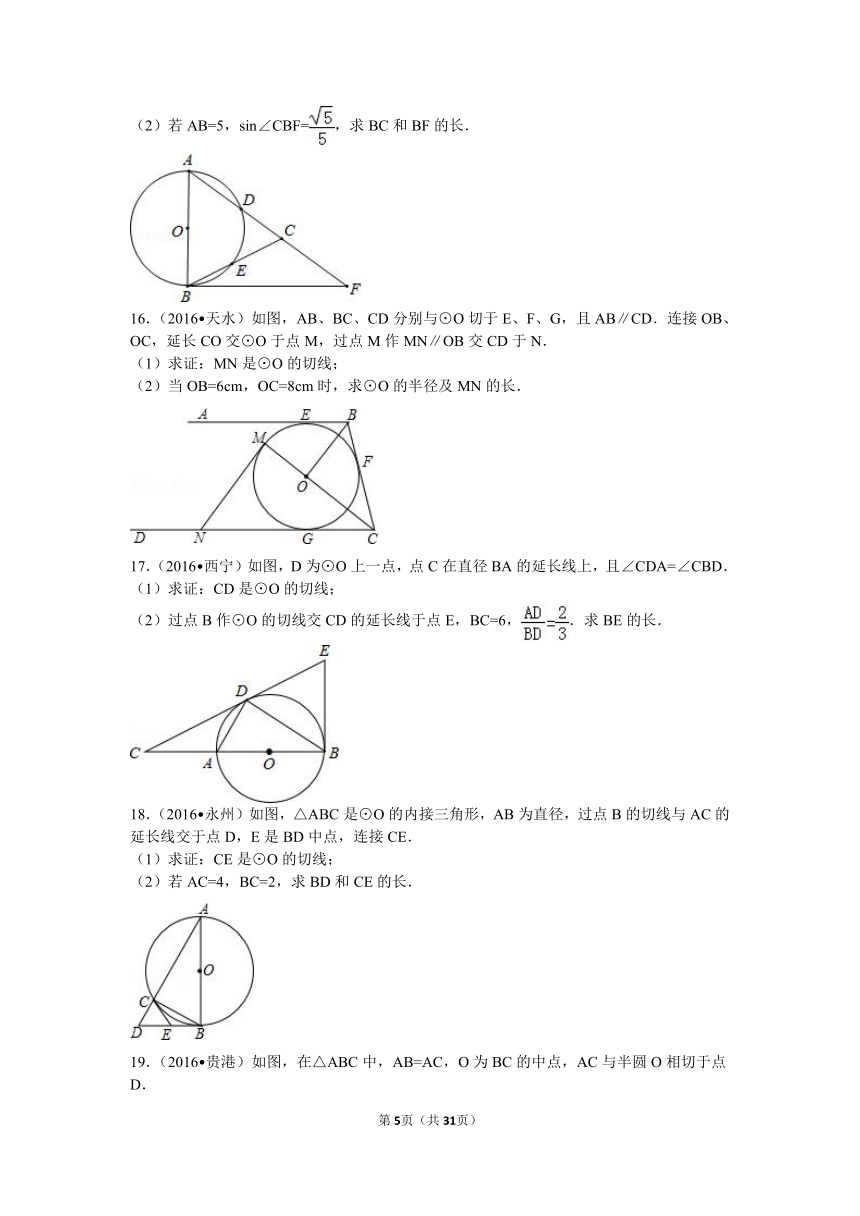
13.(2012秋 崇安区校级期末)如图,在△ABC中,AB=AC=5,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,sin∠CBF=,则BF的长为______.
14.(2010秋 北京校级期末)如图,△ABC内接于⊙O,AB是⊙O的直径,延长AB到D,连接CD.请你结合图形,编写一道题.要求:再补充两个已知条件,并写出在所有已知条件下得出的一个结论.例如:
“补充已知:OB=BD,CD切⊙O于点C,求证:∠A=∠D”
“补充已知:______.
求证:______.”
三.解答题(共6小题)
15.(2016 新疆)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
16.(2016 天水)如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
17.(2016 西宁)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,.求BE的长.
18.(2016 永州)如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
19.(2016 贵港)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.
20.(2016 宁津县二模)如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=2,AD=2,求线段BC的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2015 滦平县二模)如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4
B.8
C.4或6
D.4或8
【分析】由题意判定CD是圆的切线,从其性质在△P1EO中求得OP1,从而求得.
【解答】解:由题意CD与圆P1相切于点E,
∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒),
同理,当圆P在直线CD的右侧时,所需的时间为8秒.
综上可知:⊙P与直线CD相切时,时间为4或8秒钟,
故选D.
【点评】本题考查了切线的判定和性质,从切线入手从而解得.
2.(2015 湖北模拟)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
【分析】(1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;
(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;
(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=PO=AB;
(4)利用四边形PCBD是菱形,即可得到∠ABC=∠ABD,弧AC=弧AD.
【解答】解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
,
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴∠COA=60°,
∴∠CPO=30°,
∴CO=PO=AB,
∴PO=AB,
∵AB是⊙O的直径,CD不是直径,
∴AB≠CD,
∴PO≠DC,
故(3)错误;
(4)由(2)证得四边形PCBD是菱形,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
故(4)正确;
故选C.
【点评】此题主要考查了切线的判定与性质和全等三角形的判定与性质以及菱形的判定与性质等知识,熟练利用全等三角形的判定与性质是解题关键.
3.(2015 蒙城县校级模拟)如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE=EC,则AC是⊙O的切线
【分析】A、如图1,连接OE,根据同圆的半径相等得到OB=OE,根据等边三角形的性质得到∠BOE=∠BAC,求得OE∥AC,于是得到A选项正确;B、由于EF是⊙O的切线,得到OE⊥EF,根据平行线的性质得到B选项正确;C、根据等边三角形的性质和圆的性质得到AO=OB,如图2,过O作OH⊥AC于H,根据三角函数得到OH=AO≠OB,于是得到C选项错误;D、如图2根据等边三角形的性质和等量代换即可得到D选项正确.
【解答】解:A、如图1,连接OE,
则OB=OE,
∵∠B=60°
∴∠BOE=60°,
∵∠BAC=60°,
∴∠BOE=∠BAC,
∴OE∥AC,
∵EF⊥AC,
∴OE⊥EF,
∴EF是⊙O的切线
∴A选项正确;
B、∵EF是⊙O的切线,
∴OE⊥EF,
由A知:OE∥AC,
∴AC⊥EF,
∴B选项正确;
C、∵∠B=60°,OB=OE,
∴BE=OB,
∵BE=CE,
∴BC=AB=2BO,
∴AO=OB,
如图2,过O作OH⊥AC于H,
∵∠BAC=60°,
∴OH=AO≠OB,
∴C选项错误;
D、如图2,∵BE=EC,
∴CE=BE,
∵AB=BC,BO=BE,
∴AO=CE=OB,
∴OH=AO=OB,
∴AC是⊙O的切线,
∴D选项正确.
故选C.
【点评】本题考查了切线的判定和性质,等边三角形的性质,正确的作出辅助线是解题的关键.
4.(2014 泰安)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
【分析】(1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;
(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;
(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=PO=AB;
(4)利用四边形PCBD是菱形,∠CPO=30°,则DP=DB,则∠DPB=∠DBP=30°,求出即可.
【解答】解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
,
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴∠COA=60°,
∴∠CPO=30°,
∴CO=PO=AB,
∴PO=AB,
故(3)正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,
∴∠PDB=120°,
故(4)正确;
正确个数有4个,
故选:A.
【点评】此题主要考查了切线的判定与性质和全等三角形的判定与性质以及菱形的判定与性质等知识,熟练利用全等三角形的判定与性质是解题关键.
5.(2012 桂平市三模)如图,直线AC∥BD,⊙O与AC和BD分别相切于点A和点B.点M和点N分别是AC和BD上的动点,MN沿AC和BD平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.直线AC和BD的距离为2
B.若∠MON=90°,则MN与⊙O相切
C.若MN与⊙O相切,则AM=
D.MN=
【分析】A、根据切线的性质知直线AC和BD的距离为该圆的直径;
B、当MN与圆O相切时,求出∠MON度数即可做出判断;
C、当MN与圆O相切时,设切点为E,连接OE,OM,利用切线长定理得到MA=ME,且MO为角平分线,求出∠AMO为30°,在直角三角形AOM中,由OA及tan30°,求出AM,即可做出判断;
D、过M作MF垂直于BD,可得出MF=AB=2,在直角三角形MNF中,由∠MNF的度数及MF的长,利用锐角三角函数定义求出MN的长,即可做出判断.
【解答】解:A、∵⊙O与AC和BD分别相切于点A和点B,
∴AB⊥AC,AB⊥BD,
∵AC∥BD,
∴A,O,B三点共线,
∴直线AC与BD间的距离为直径AB=2,本选项正确;
B、若∠MON=90°,则MN不一定与⊙O相切,本选项错误;
C、当MN与⊙O相切时切点为E点,连接OM,OE,
∴MA=ME,MO为∠AME平分线,
∵∠AME=60°,
∴∠AMO=30°,
在Rt△AOM中,OA=1,
∴AM==,本选项正确;
D、作MF⊥BD,
∵AC∥BD,
∴∠MNF=∠AME=60°,
∵MF=AB=2,
在Rt△MNF中,MF=2,∠MNF=60°,
∴MN==,本选项正确;
故选B
【点评】此题考查了切线的判定与性质,熟练掌握切线的判定与性质是解本题的关键.
6.(2012秋 汉阳区期中)如图,在梯形ABCD中,AB∥DC.
①若∠A=90°,AB+CD=BC,则以AD为直径的圆与BC相切;
②若∠A=90°,当以AD为直径的圆与BC相切,则以BC为直径的圆也与AD相切;
③若以AD为直径的圆与BC相切,则AB+CD=BC;
④若以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.
以上判断正确的个数有( )
A.1
B.2
C.3
D.4
【分析】①作AD的中点E,作EG⊥BC于点G,过E作AB的平行线EF,则EF是梯形ABCD的中位线,然后证明△DCE≌△GCE,根据切线的判定定理即可判断;
②若∠A=90°,当以AD为直径的圆与BC相切,设以AD为直径的圆的圆心是E,则E是AD的中点,设圆与BC相切与点G,则连接EG,可以利用全等三角形的性质证得AB+CD=BC,然后取BC的中点F,中位线EF就是以BC为直径的圆的圆心到AD的垂线段,根据切线的判定定理即可证得;
③需要条件∠A=90°.
④由面积法,可得以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.
【解答】解:①作AD的中点E,作EG⊥BC于点G,过E作AB的平行线EF,则EF是梯形ABCD的中位线,
∴EF=(AB+CD)=BC=CF,
∴∠CEF=∠ECF,
∵EF∥CD,
∴∠DCE=∠CEF,
∵在△DCE和△GCE中,
,
∴△DCE≌△GCE(AAS),
∴EG=DE=AD,则以AD为直径的圆与BC相切.
故命题正确;
②若∠A=90°,当以AD为直径的圆与BC相切,设以AD为直径的圆的圆心是E,则E是AD的中点,设圆与BC相切与点G,
则连接EG,则EG⊥BC,且EG=ED.
∵在Rt△DCE和Rt△GCE中,
,
∴Rt△DCE≌Rt△GCE(HL),
∴CG=CD,
同理,BG=AB,
∴AB+CD=BC,
取BC的中点,连接EF,则EF是梯形ABCD的中位线,
∴EF=(AB+CD)=BC,
又∵若∠A=90°,则EF⊥AD,
∴以BC为直径的圆也与AD相切.故②正确;
③需要∠A=90°,故错误.
④由面积法,可得以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.正确.
故正确的是:①②④.故选C.
【点评】本题考查了全等三角形的判定与性质,切线的判定与性质,梯形的中位线的性质,正确作出辅助线是关键.
7.(2009秋 常熟市期末)如图,线段AB是⊙O的直径,⊙O交线段BC于D,且D是BC中点,DE⊥AC于E,连接AD,则下列结论正确的个数是( )
①CE CA=CD CB;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线;⑤AD2=AE AB.
A.2个
B.3个
C.4个
D.5个
【分析】由DE与AC垂直,得到三角形CDE为直角三角形,而由AB为圆的直径,根据直径所对的圆周角为90°,得到AD与BC垂直,又D为BC中点,进而得到AD垂直平分BC,根据线段垂直平分线的性质得到AC与AB相等,故三角形ABC不是直角三角形,所以三角形CDE与ABC不相似,CE CA与CD CB不相等,选项①错误;由O为AB中点,得到AO为AB的一半,故AO为AC的一半,选项③正确;由OD为三角形ABC的中位线,根据三角形的中位线定理得到OD与AC平行,由AC与DE垂直得到OD与DE垂直,即∠ODE为90°,故DE为圆O的切线,选项④正确;由两对对应角相等得到三角形ADE与三角形ACD相似,根据对应边成比例得到选项⑤正确,从而得到所有正确选项的个数.
【解答】解:显然,△CED为直角三角形,而△ABC不是直角三角形,故两三角形不相似,
所以CE CA≠CD CB,选项①错误;
连接OD,∵D为BC中点,O为AB中点,
∴DO为△ABC的中位线,
∴OD∥AC,
又DE⊥AC,∴∠DEA=90°,
∴∠ODE=90°,
∴DE为圆O的切线,选项④正确;
又OB=OD,∴∠ODB=∠B,
∵AB为圆O的直径,∴∠ADB=90°,
∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,
∴∠EDA=∠BDO,
∴∠EDA=∠B,选项②正确;
由D为BC中点,且AD⊥BC,
∴AD垂直平分BC,
∴AC=AB,又OA=AB,
∴OA=AC,选项③正确;
∵∠DAC=∠EAD,∠DEA=∠CDA=90°,
∴△ADE∽△ACD,
∴=,即AD2=AE AB,选项⑤正确;
则正确结论的个数为4个.
故选C.
【点评】此题考查了相似三角形的判定与性质,切线的判定,及三角形的中位线定理.证明切线时连接OD是解这类题经常连接的辅助线.
8.(2007 上海校级模拟)下列命题中,假命题是( )
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
【分析】根据切线的定义和性质进行解答(要正确理解切线的定义:和圆有唯一公共点的直线是圆的切线.
掌握切线的判定:①经过半径的外端,且垂直于这条半径的直线,是圆的切线;
②到圆心的距离等于半径的直线是该圆的切线).
【解答】解:A、经过半径的外端点且垂直于这条半径的直线是圆的切线;可能经过圆心,故本选项错误;
B、圆的切线的判定定理:经过直径的端点且垂直于这条直径的直线是圆的切线;故本选项正确,故不符合题意;
C、圆的切线垂直于经过切点的半径;故本选项正确,故不符合题意;
D、经过切点且垂直于切线的直线为圆的直径,所以它经过圆心;故本选项正确,故不符合题意;
故选A.
【点评】本题考查了切线的判定与性质、命题与定理.注意,切线与圆有且只有一个公共点,所以经过半径的外端点且垂直于这条半径的直线是圆的切线.
9.(2016 厦门校级二模)如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
①l1和l2的距离为2
②MN=
③当直线MN与⊙O相切时,∠MON=90°
④当AM+BN=时,直线MN与⊙O相切.正确的个数是( )
A.1
B.2
C.3
D.4
【分析】如图1,利用切线的性质得到OA⊥l1,OB⊥l2,再证明点A、B、O共线即可得到l1和l2的距离为2,则可对①进行判断;作NH⊥AM,如图1,易得四边形ABNH为矩形,则NH=AB=2,然后在Rt△MNH中利用含30度的直角三角形三边的关系可计算出MN,从而可对②进行判断;当直线MN与⊙O相切时,如图2,利用切线长定理得到∠1=∠2,∠3=∠4,然后根据平行线的性质和三角形内角和可计算出∠MON的度数,则可对③进行判断;过点O作OC⊥MN于C,如图2,根据梯形的面积和三角形面积公式,利用S四边形ABNM=S△OAM+S△OMN+S△OBN得到 1 AM+ 1 BN+MN OC=(BN+AM) 2,则根据AM+BN=,MN=可计算出OC=1,然后根据切线的判定定理可判断直线MN与⊙O相切,则可对④进行判断.
【解答】解:如图1,∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、B、O共线,
∴l1和l2的距离=AB=2,所以①正确;
作NH⊥AM,如图1,则四边形ABNH为矩形,
∴NH=AB=2,
在Rt△MNH中,∵∠1=60°,
∴MH=NH=,
∴MN=2MH=,所以②正确;
当直线MN与⊙O相切时,如图2,∠1=∠2,∠3=∠4,
∵l1∥l2,
∴∠1+∠2+∠3+∠4=180°,
∴∠1+∠3=90°,
∴∠MON=90°,所以③正确;
过点O作OC⊥MN于C,如图2,
∵S四边形ABNM=S△OAM+S△OMN+S△OBN,
∴ 1 AM+ 1 BN+MN OC=(BN+AM) 2,
即(AM+BN)+MN OC=AM+BN,
∵AM+BN=,MN=,
∴OC=1,
而OC⊥MN,
∴直线MN与⊙O相切,所以④正确.
故选D.
【点评】本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.常见的辅助线的:判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;
有切线时,常常“遇到切点连圆心得半径”.
10.(2009 硚口区一模)已知⊙O是△ABC的外接圆,⊙O半径为R,AD是△ABC的高,E是
的中点,EF与⊙O切于E,交AC的延长线于F,则下列结论:
①AC AB=2R AD;
②EF∥BC;
③CF AC=EF CM;
④.
其中正确的结论是( )
A.①②③
B.①③④
C.②③④
D.①②③④
【分析】①连接AO并延长交⊙O于G点,连接CG,则∠GCA=∠ADB=90°,∠G=∠B,证明△ACG∽△ADB,利用相似比证明结论;
②连接OE,由EF为⊙O的切线可知OE⊥EF,由E是
的中点可知OE⊥BC,故结论成立;
③连接CE,证明△ACM∽△EFC,利用相似比证明结论;
④过M点分别作MP⊥AC,MQ⊥AB,由E是
的中点可知AE平分∠BAC,由角平分线的性质得MP=MQ,而∠F=∠PCM,在Rt△PCM和Rt△BDQ中,分别表示sin∠B,sin∠PCM,再求比.
【解答】解:①如图1,连接AO并延长交⊙O于G点,连接CG,
∵AG为直径,∴∠GCA=∠ADB=90°,又∠G=∠B,
∴△ACG∽△ADB,∴=,AG=2R,∴AC AB=2R AD,①正确;
②如图1,连接OE,
∵EF为⊙O的切线,E为切点,∴OE⊥EF,
又∵E是
的中点,∴OE⊥BC,
∴EF∥BC,②正确;
③如图2,连接CE,
∵EF∥BC,∴∠ACM=∠F,
由弦切角定理可知∠CAE=∠FEC,∴△ACM∽△EFC,
∴=,即CF AC=EF CM,③正确;
④如图2,过M点分别作MP⊥AC,MQ⊥AB,垂足为P,Q,
∵E是
的中点,∴AE平分∠BAC,∴MP=MQ,
又∠F=∠PCM,∴在Rt△PCM中,sin∠PCM=sinF=,
在Rt△BMQ中,sinB=,
∴=,④正确.
故选D.
【点评】本题考查了切线的性质,平行线的判定与性质,圆周角定理,相似三角形的判定与性质,角平分线的判定与性质,锐角三角函数的定义.关键是通过作辅助线,将问题转化到直角三角形中求解.
二.填空题(共4小题)
11.(2015 哈尔滨模拟)如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=,BD=2,则线段AE的长为 .
【分析】先求出∠DAB=∠E,证明△ABD∽△EAD,得出,即可求出AE=.
【解答】解:∵EA⊥AB,
∴∠EAB=90°,
∴∠B+∠E=90得,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD=,∠ADB=∠EAB,∠B+∠DAB=90°,
∴∠DAB=∠E,
∴△ABD∽△EAD,
∴∠DAB=∠E,
∴,,
∴AE=.
故答案为:.
【点评】本题考查了相似三角形的判定与性质;证明三角形相似得出比例式是解决问题的关键.
12.(2015 河南模拟)如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=,则PA的长为 1 .
【分析】根据已知可证△AOD为等边三角形,∠P=30°,PA=AD=OA,再证明PD是切线,根据切割线定理即可得出结果.
【解答】解:∵AB为直径,
∴∠ADB=90°,
∵∠BDE=60°,
∴∠PDA=180°﹣90°﹣60°=30°,
∴∠PBD=∠PDA=30°,
∵OB=OD,
∴∠ODB=∠PBD=30°,
∴∠ADO=60°,
∴△ADO为等边三角形,∠ODP=90°,
∴AD=OA,∠AOD=60°,PD为⊙O的切线,
∴∠P=30°,
∴PA=AD,PD2=PA PB,
∴(=PA 3PA
∴PA=1;
故答案为:1.
【点评】本题考查了圆周角定理、等边三角形的判定与性质、切线的判定与性质;证明三角形是等边三角形是解决问题的关键.
13.(2012秋 崇安区校级期末)如图,在△ABC中,AB=AC=5,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,sin∠CBF=,则BF的长为 .
【分析】因为AB为直径,所以连结AE,则可知过∠BAE=∠CBF,点C作CG∥BF,在Rt△ABE中可求得BE,进一步求得BC,在Rt△CGB中求出CG和GB,再利用平行线分线段成比例可求得.
【解答】解:连结AE,
∵AB是圆O的直径,
∴∠AEB=90°
∴∠1+∠2=90°
∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB,
∴∠1=∠CBF.
过点C作CG⊥AB于点G,
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1═,
∵∠AEB=90°,AB=5,
∴BE=AB sin∠1=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE=,
∴sin∠2=,cos∠2=,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴,
∴BF=.
故答案我:.
【点评】此题主要考查圆的有关性质及平行线分线段定理的应用,解题的关键是如何利用已知条件中的sin∠CBF=,属于中档题,有一定的难度.
14.(2010秋 北京校级期末)如图,△ABC内接于⊙O,AB是⊙O的直径,延长AB到D,连接CD.请你结合图形,编写一道题.要求:再补充两个已知条件,并写出在所有已知条件下得出的一个结论.例如:
“补充已知:OB=BD,CD切⊙O于点C,求证:∠A=∠D”
“补充已知: 条件:∠A=∠D,CD是⊙O的切线. .
求证: 结论:的度数为60° .”
【分析】添加∠A=∠D,CD是⊙O的切线,可以通过作辅助线OC,求出∠COB=90°,从而证出的度数为60°.
【解答】解:已知:∠A=∠D,CD是⊙O的切线,
求证:的度数为60°.
证明:连接OC,
则∠OCD=90°,
设∠A=∠ACO=∠D=x度,
在△ACO中,∠COD=2x度,
∴在直角三角形OCD中,2x+x=90,
解得x=30,
∴∠COD=60°.
【点评】本题是一道开放题,条件、结论、过程全开放,要有一定的知识积累方可正确解答.
三.解答题(共6小题)
15.(2016 新疆)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
【分析】(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)利用已知条件证得△AGC∽△ABF,利用比例式求得线段的长即可.
【解答】(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于G.
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=,
∵在Rt△AEB中,∠AEB=90°,AB=5,
∴BE=AB sin∠1=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE==2,
∴sin∠2===,cos∠2===,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴
∴BF==
【点评】本题考查常见的几何题型,包括切线的判定,角的大小及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.
16.(2016 天水)如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
【分析】(1)求证:MN是⊙O的切线,就可以证明∠NMC=90°
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,根据△NMC∽△BOC就可以求出MN的长.
【解答】(1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G
∴∠OBC=∠ABC,∠DCB=2∠DCM(1分)
∵AB∥CD
∴∠ABC+∠DCB=180°
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣90°=90°(2分)
∵MN∥OB
∴∠NMC=∠BOC=90°
即MN⊥MC
且MO是⊙O的半径
∴MN是⊙O的切线(4分)
(2)解:连接OF,则OF⊥BC(5分)
由(1)知,△BOC是直角三角形,
∴BC===10,
∵S△BOC= OB OC= BC OF
∴6×8=10×OF
∴0F=4.8cm
∴⊙O的半径为4.8cm(6分)
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°
∴△NMC∽△BOC(7分)
∴,即=,
∴MN=9.6(cm).(8分)
【点评】本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
17.(2016 西宁)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,.求BE的长.
【分析】(1)连OD,OE,根据圆周角定理得到∠ADO+∠ODB=90°,而∠CDA=∠CBD,∠CBD=∠ODB,于是∠CDA+∠ADO=90°;
(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
【解答】(1)证明:连结OD,
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
又∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∵OD是⊙O半径,
∴CD是⊙O的切线
(2)解:∵∠C=∠C,∠CDA=∠CBD
∴△CDA∽△CBD
∴
∵,BC=6,
∴CD=4,
∵CE,BE是⊙O的切线
∴BE=DE,BE⊥BC
∴BE2+BC2=EC2,即BE2+62=(4+BE)2
解得:BE=.
【点评】本题考查了切线的判定与性质:过半径的外端点与半径垂直的直线是圆的切线;也考查了圆周角定理的推论以及三角形相似的判定与性质.
18.(2016 永州)如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
【分析】(1)连接OC,由弦切角定理和切线的性质得出∠CBE=∠A,∠ABD=90°,由圆周角定理得出∠ACB=90°,得出∠ACO+∠BCO=90°,∠BCD=90°,由直角三角形斜边上的中线性质得出CE=BD=BE,得出∠BCE=∠CBE=∠A,证出∠ACO=∠BCE,得出∠BCE+∠BCO=90°,得出CE⊥OC,即可得出结论;
(2)由勾股定理求出AB,再由三角函数得出tanA===,求出BD=AB=,即可得出CE的长.
【解答】(1)证明:连接OC,如图所示:
∵BD是⊙O的切线,
∴∠CBE=∠A,∠ABD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,∠BCD=90°,
∵E是BD中点,
∴CE=BD=BE,
∴∠BCE=∠CBE=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴∠ACO=∠BCE,
∴∠BCE+∠BCO=90°,
即∠OCE=90°,CE⊥OC,
∴CE是⊙O的切线;
(2)解:∵∠ACB=90°,
∴AB===2,
∵tanA====,
∴BD=AB=,
∴CE=BD=.
【点评】本题考查了切线的判定、弦切角定理、圆周角定理、直角三角形斜边上的中线性质、勾股定理、三角函数等知识;熟练掌握切线的判定和圆周角定理是解决问题的关键.
19.(2016 贵港)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.
【分析】(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;
(2)根据余弦,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
【解答】(1)证明:如图1
,
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=,AB=12,得
OB=8.
由勾股定理,得
AO==4.
由三角形的面积,得
S△AOB=AB OE=OB AO,
OE==,
半圆O所在圆的半径是.
【点评】本题考查了切线的判定与性质,利用切线的判定是解题关键,利用面积相等得出关于OE的长是解题关键.
20.(2016 宁津县二模)如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=2,AD=2,求线段BC的长.
【分析】(1)因为BC经过圆的半径的外端,只要证明AB⊥BC即可.连接OE、OC,利用△OBC≌△OEC,得到∠OBC=90°即可证明BC为⊙O的切线.
(2)作DF⊥BC于点F,构造Rt△DFC,利用勾股定理解答即可.
【解答】(1)证明:连接OE、OC.
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
(2)解:过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2.
∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2)2,解得x=.
∴BC=.
【点评】此题考查了切线的判定和勾股定理的应用,作出辅助线构造直角三角形和全等三角形是解题的关键.
第1页(共1页)
一.选择题(共10小题)
1.(2015 滦平县二模)如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4
B.8
C.4或6
D.4或8
2.(2015 湖北模拟)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
3.(2015 蒙城县校级模拟)如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE=EC,则AC是⊙O的切线
4.(2014 泰安)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
5.(2012 桂平市三模)如图,直线AC∥BD,⊙O与AC和BD分别相切于点A和点B.点M和点N分别是AC和BD上的动点,MN沿AC和BD平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.直线AC和BD的距离为2
B.若∠MON=90°,则MN与⊙O相切
C.若MN与⊙O相切,则AM=
D.MN=
6.(2012秋 汉阳区期中)如图,在梯形ABCD中,AB∥DC.
①若∠A=90°,AB+CD=BC,则以AD为直径的圆与BC相切;
②若∠A=90°,当以AD为直径的圆与BC相切,则以BC为直径的圆也与AD相切;
③若以AD为直径的圆与BC相切,则AB+CD=BC;
④若以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.
以上判断正确的个数有( )
A.1
B.2
C.3
D.4
7.(2009秋 常熟市期末)如图,线段AB是⊙O的直径,⊙O交线段BC于D,且D是BC中点,DE⊥AC于E,连接AD,则下列结论正确的个数是( )
①CE CA=CD CB;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线;⑤AD2=AE AB.
A.2个
B.3个
C.4个
D.5个
8.(2007 上海校级模拟)下列命题中,假命题是( )
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
9.(2016 厦门校级二模)如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
①l1和l2的距离为2
②MN=
③当直线MN与⊙O相切时,∠MON=90°
④当AM+BN=时,直线MN与⊙O相切.正确的个数是( )
A.1
B.2
C.3
D.4
10.(2009 硚口区一模)已知⊙O是△ABC的外接圆,⊙O半径为R,AD是△ABC的高,E是
的中点,EF与⊙O切于E,交AC的延长线于F,则下列结论:
①AC AB=2R AD;
②EF∥BC;
③CF AC=EF CM;
④.
其中正确的结论是( )
A.①②③
B.①③④
C.②③④
D.①②③④
二.填空题(共4小题)
11.(2015 哈尔滨模拟)如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=,BD=2,则线段AE的长为______.
12.(2015 河南模拟)如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=,则PA的长为______.
13.(2012秋 崇安区校级期末)如图,在△ABC中,AB=AC=5,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,sin∠CBF=,则BF的长为______.
14.(2010秋 北京校级期末)如图,△ABC内接于⊙O,AB是⊙O的直径,延长AB到D,连接CD.请你结合图形,编写一道题.要求:再补充两个已知条件,并写出在所有已知条件下得出的一个结论.例如:
“补充已知:OB=BD,CD切⊙O于点C,求证:∠A=∠D”
“补充已知:______.
求证:______.”
三.解答题(共6小题)
15.(2016 新疆)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
16.(2016 天水)如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
17.(2016 西宁)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,.求BE的长.
18.(2016 永州)如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
19.(2016 贵港)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.
20.(2016 宁津县二模)如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=2,AD=2,求线段BC的长.
参考答案与试题解析
一.选择题(共10小题)
1.(2015 滦平县二模)如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4
B.8
C.4或6
D.4或8
【分析】由题意判定CD是圆的切线,从其性质在△P1EO中求得OP1,从而求得.
【解答】解:由题意CD与圆P1相切于点E,
∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒),
同理,当圆P在直线CD的右侧时,所需的时间为8秒.
综上可知:⊙P与直线CD相切时,时间为4或8秒钟,
故选D.
【点评】本题考查了切线的判定和性质,从切线入手从而解得.
2.(2015 湖北模拟)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
【分析】(1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;
(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;
(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=PO=AB;
(4)利用四边形PCBD是菱形,即可得到∠ABC=∠ABD,弧AC=弧AD.
【解答】解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
,
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴∠COA=60°,
∴∠CPO=30°,
∴CO=PO=AB,
∴PO=AB,
∵AB是⊙O的直径,CD不是直径,
∴AB≠CD,
∴PO≠DC,
故(3)错误;
(4)由(2)证得四边形PCBD是菱形,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
故(4)正确;
故选C.
【点评】此题主要考查了切线的判定与性质和全等三角形的判定与性质以及菱形的判定与性质等知识,熟练利用全等三角形的判定与性质是解题关键.
3.(2015 蒙城县校级模拟)如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE=EC,则AC是⊙O的切线
【分析】A、如图1,连接OE,根据同圆的半径相等得到OB=OE,根据等边三角形的性质得到∠BOE=∠BAC,求得OE∥AC,于是得到A选项正确;B、由于EF是⊙O的切线,得到OE⊥EF,根据平行线的性质得到B选项正确;C、根据等边三角形的性质和圆的性质得到AO=OB,如图2,过O作OH⊥AC于H,根据三角函数得到OH=AO≠OB,于是得到C选项错误;D、如图2根据等边三角形的性质和等量代换即可得到D选项正确.
【解答】解:A、如图1,连接OE,
则OB=OE,
∵∠B=60°
∴∠BOE=60°,
∵∠BAC=60°,
∴∠BOE=∠BAC,
∴OE∥AC,
∵EF⊥AC,
∴OE⊥EF,
∴EF是⊙O的切线
∴A选项正确;
B、∵EF是⊙O的切线,
∴OE⊥EF,
由A知:OE∥AC,
∴AC⊥EF,
∴B选项正确;
C、∵∠B=60°,OB=OE,
∴BE=OB,
∵BE=CE,
∴BC=AB=2BO,
∴AO=OB,
如图2,过O作OH⊥AC于H,
∵∠BAC=60°,
∴OH=AO≠OB,
∴C选项错误;
D、如图2,∵BE=EC,
∴CE=BE,
∵AB=BC,BO=BE,
∴AO=CE=OB,
∴OH=AO=OB,
∴AC是⊙O的切线,
∴D选项正确.
故选C.
【点评】本题考查了切线的判定和性质,等边三角形的性质,正确的作出辅助线是解题的关键.
4.(2014 泰安)如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
【分析】(1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;
(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;
(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=PO=AB;
(4)利用四边形PCBD是菱形,∠CPO=30°,则DP=DB,则∠DPB=∠DBP=30°,求出即可.
【解答】解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
,
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴∠COA=60°,
∴∠CPO=30°,
∴CO=PO=AB,
∴PO=AB,
故(3)正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,
∴∠PDB=120°,
故(4)正确;
正确个数有4个,
故选:A.
【点评】此题主要考查了切线的判定与性质和全等三角形的判定与性质以及菱形的判定与性质等知识,熟练利用全等三角形的判定与性质是解题关键.
5.(2012 桂平市三模)如图,直线AC∥BD,⊙O与AC和BD分别相切于点A和点B.点M和点N分别是AC和BD上的动点,MN沿AC和BD平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A.直线AC和BD的距离为2
B.若∠MON=90°,则MN与⊙O相切
C.若MN与⊙O相切,则AM=
D.MN=
【分析】A、根据切线的性质知直线AC和BD的距离为该圆的直径;
B、当MN与圆O相切时,求出∠MON度数即可做出判断;
C、当MN与圆O相切时,设切点为E,连接OE,OM,利用切线长定理得到MA=ME,且MO为角平分线,求出∠AMO为30°,在直角三角形AOM中,由OA及tan30°,求出AM,即可做出判断;
D、过M作MF垂直于BD,可得出MF=AB=2,在直角三角形MNF中,由∠MNF的度数及MF的长,利用锐角三角函数定义求出MN的长,即可做出判断.
【解答】解:A、∵⊙O与AC和BD分别相切于点A和点B,
∴AB⊥AC,AB⊥BD,
∵AC∥BD,
∴A,O,B三点共线,
∴直线AC与BD间的距离为直径AB=2,本选项正确;
B、若∠MON=90°,则MN不一定与⊙O相切,本选项错误;
C、当MN与⊙O相切时切点为E点,连接OM,OE,
∴MA=ME,MO为∠AME平分线,
∵∠AME=60°,
∴∠AMO=30°,
在Rt△AOM中,OA=1,
∴AM==,本选项正确;
D、作MF⊥BD,
∵AC∥BD,
∴∠MNF=∠AME=60°,
∵MF=AB=2,
在Rt△MNF中,MF=2,∠MNF=60°,
∴MN==,本选项正确;
故选B
【点评】此题考查了切线的判定与性质,熟练掌握切线的判定与性质是解本题的关键.
6.(2012秋 汉阳区期中)如图,在梯形ABCD中,AB∥DC.
①若∠A=90°,AB+CD=BC,则以AD为直径的圆与BC相切;
②若∠A=90°,当以AD为直径的圆与BC相切,则以BC为直径的圆也与AD相切;
③若以AD为直径的圆与BC相切,则AB+CD=BC;
④若以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.
以上判断正确的个数有( )
A.1
B.2
C.3
D.4
【分析】①作AD的中点E,作EG⊥BC于点G,过E作AB的平行线EF,则EF是梯形ABCD的中位线,然后证明△DCE≌△GCE,根据切线的判定定理即可判断;
②若∠A=90°,当以AD为直径的圆与BC相切,设以AD为直径的圆的圆心是E,则E是AD的中点,设圆与BC相切与点G,则连接EG,可以利用全等三角形的性质证得AB+CD=BC,然后取BC的中点F,中位线EF就是以BC为直径的圆的圆心到AD的垂线段,根据切线的判定定理即可证得;
③需要条件∠A=90°.
④由面积法,可得以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.
【解答】解:①作AD的中点E,作EG⊥BC于点G,过E作AB的平行线EF,则EF是梯形ABCD的中位线,
∴EF=(AB+CD)=BC=CF,
∴∠CEF=∠ECF,
∵EF∥CD,
∴∠DCE=∠CEF,
∵在△DCE和△GCE中,
,
∴△DCE≌△GCE(AAS),
∴EG=DE=AD,则以AD为直径的圆与BC相切.
故命题正确;
②若∠A=90°,当以AD为直径的圆与BC相切,设以AD为直径的圆的圆心是E,则E是AD的中点,设圆与BC相切与点G,
则连接EG,则EG⊥BC,且EG=ED.
∵在Rt△DCE和Rt△GCE中,
,
∴Rt△DCE≌Rt△GCE(HL),
∴CG=CD,
同理,BG=AB,
∴AB+CD=BC,
取BC的中点,连接EF,则EF是梯形ABCD的中位线,
∴EF=(AB+CD)=BC,
又∵若∠A=90°,则EF⊥AD,
∴以BC为直径的圆也与AD相切.故②正确;
③需要∠A=90°,故错误.
④由面积法,可得以AD为直径的圆与BC相切,则以BC为直径的圆与AD相切.正确.
故正确的是:①②④.故选C.
【点评】本题考查了全等三角形的判定与性质,切线的判定与性质,梯形的中位线的性质,正确作出辅助线是关键.
7.(2009秋 常熟市期末)如图,线段AB是⊙O的直径,⊙O交线段BC于D,且D是BC中点,DE⊥AC于E,连接AD,则下列结论正确的个数是( )
①CE CA=CD CB;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线;⑤AD2=AE AB.
A.2个
B.3个
C.4个
D.5个
【分析】由DE与AC垂直,得到三角形CDE为直角三角形,而由AB为圆的直径,根据直径所对的圆周角为90°,得到AD与BC垂直,又D为BC中点,进而得到AD垂直平分BC,根据线段垂直平分线的性质得到AC与AB相等,故三角形ABC不是直角三角形,所以三角形CDE与ABC不相似,CE CA与CD CB不相等,选项①错误;由O为AB中点,得到AO为AB的一半,故AO为AC的一半,选项③正确;由OD为三角形ABC的中位线,根据三角形的中位线定理得到OD与AC平行,由AC与DE垂直得到OD与DE垂直,即∠ODE为90°,故DE为圆O的切线,选项④正确;由两对对应角相等得到三角形ADE与三角形ACD相似,根据对应边成比例得到选项⑤正确,从而得到所有正确选项的个数.
【解答】解:显然,△CED为直角三角形,而△ABC不是直角三角形,故两三角形不相似,
所以CE CA≠CD CB,选项①错误;
连接OD,∵D为BC中点,O为AB中点,
∴DO为△ABC的中位线,
∴OD∥AC,
又DE⊥AC,∴∠DEA=90°,
∴∠ODE=90°,
∴DE为圆O的切线,选项④正确;
又OB=OD,∴∠ODB=∠B,
∵AB为圆O的直径,∴∠ADB=90°,
∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,
∴∠EDA=∠BDO,
∴∠EDA=∠B,选项②正确;
由D为BC中点,且AD⊥BC,
∴AD垂直平分BC,
∴AC=AB,又OA=AB,
∴OA=AC,选项③正确;
∵∠DAC=∠EAD,∠DEA=∠CDA=90°,
∴△ADE∽△ACD,
∴=,即AD2=AE AB,选项⑤正确;
则正确结论的个数为4个.
故选C.
【点评】此题考查了相似三角形的判定与性质,切线的判定,及三角形的中位线定理.证明切线时连接OD是解这类题经常连接的辅助线.
8.(2007 上海校级模拟)下列命题中,假命题是( )
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
【分析】根据切线的定义和性质进行解答(要正确理解切线的定义:和圆有唯一公共点的直线是圆的切线.
掌握切线的判定:①经过半径的外端,且垂直于这条半径的直线,是圆的切线;
②到圆心的距离等于半径的直线是该圆的切线).
【解答】解:A、经过半径的外端点且垂直于这条半径的直线是圆的切线;可能经过圆心,故本选项错误;
B、圆的切线的判定定理:经过直径的端点且垂直于这条直径的直线是圆的切线;故本选项正确,故不符合题意;
C、圆的切线垂直于经过切点的半径;故本选项正确,故不符合题意;
D、经过切点且垂直于切线的直线为圆的直径,所以它经过圆心;故本选项正确,故不符合题意;
故选A.
【点评】本题考查了切线的判定与性质、命题与定理.注意,切线与圆有且只有一个公共点,所以经过半径的外端点且垂直于这条半径的直线是圆的切线.
9.(2016 厦门校级二模)如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
①l1和l2的距离为2
②MN=
③当直线MN与⊙O相切时,∠MON=90°
④当AM+BN=时,直线MN与⊙O相切.正确的个数是( )
A.1
B.2
C.3
D.4
【分析】如图1,利用切线的性质得到OA⊥l1,OB⊥l2,再证明点A、B、O共线即可得到l1和l2的距离为2,则可对①进行判断;作NH⊥AM,如图1,易得四边形ABNH为矩形,则NH=AB=2,然后在Rt△MNH中利用含30度的直角三角形三边的关系可计算出MN,从而可对②进行判断;当直线MN与⊙O相切时,如图2,利用切线长定理得到∠1=∠2,∠3=∠4,然后根据平行线的性质和三角形内角和可计算出∠MON的度数,则可对③进行判断;过点O作OC⊥MN于C,如图2,根据梯形的面积和三角形面积公式,利用S四边形ABNM=S△OAM+S△OMN+S△OBN得到 1 AM+ 1 BN+MN OC=(BN+AM) 2,则根据AM+BN=,MN=可计算出OC=1,然后根据切线的判定定理可判断直线MN与⊙O相切,则可对④进行判断.
【解答】解:如图1,∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、B、O共线,
∴l1和l2的距离=AB=2,所以①正确;
作NH⊥AM,如图1,则四边形ABNH为矩形,
∴NH=AB=2,
在Rt△MNH中,∵∠1=60°,
∴MH=NH=,
∴MN=2MH=,所以②正确;
当直线MN与⊙O相切时,如图2,∠1=∠2,∠3=∠4,
∵l1∥l2,
∴∠1+∠2+∠3+∠4=180°,
∴∠1+∠3=90°,
∴∠MON=90°,所以③正确;
过点O作OC⊥MN于C,如图2,
∵S四边形ABNM=S△OAM+S△OMN+S△OBN,
∴ 1 AM+ 1 BN+MN OC=(BN+AM) 2,
即(AM+BN)+MN OC=AM+BN,
∵AM+BN=,MN=,
∴OC=1,
而OC⊥MN,
∴直线MN与⊙O相切,所以④正确.
故选D.
【点评】本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.常见的辅助线的:判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;
有切线时,常常“遇到切点连圆心得半径”.
10.(2009 硚口区一模)已知⊙O是△ABC的外接圆,⊙O半径为R,AD是△ABC的高,E是
的中点,EF与⊙O切于E,交AC的延长线于F,则下列结论:
①AC AB=2R AD;
②EF∥BC;
③CF AC=EF CM;
④.
其中正确的结论是( )
A.①②③
B.①③④
C.②③④
D.①②③④
【分析】①连接AO并延长交⊙O于G点,连接CG,则∠GCA=∠ADB=90°,∠G=∠B,证明△ACG∽△ADB,利用相似比证明结论;
②连接OE,由EF为⊙O的切线可知OE⊥EF,由E是
的中点可知OE⊥BC,故结论成立;
③连接CE,证明△ACM∽△EFC,利用相似比证明结论;
④过M点分别作MP⊥AC,MQ⊥AB,由E是
的中点可知AE平分∠BAC,由角平分线的性质得MP=MQ,而∠F=∠PCM,在Rt△PCM和Rt△BDQ中,分别表示sin∠B,sin∠PCM,再求比.
【解答】解:①如图1,连接AO并延长交⊙O于G点,连接CG,
∵AG为直径,∴∠GCA=∠ADB=90°,又∠G=∠B,
∴△ACG∽△ADB,∴=,AG=2R,∴AC AB=2R AD,①正确;
②如图1,连接OE,
∵EF为⊙O的切线,E为切点,∴OE⊥EF,
又∵E是
的中点,∴OE⊥BC,
∴EF∥BC,②正确;
③如图2,连接CE,
∵EF∥BC,∴∠ACM=∠F,
由弦切角定理可知∠CAE=∠FEC,∴△ACM∽△EFC,
∴=,即CF AC=EF CM,③正确;
④如图2,过M点分别作MP⊥AC,MQ⊥AB,垂足为P,Q,
∵E是
的中点,∴AE平分∠BAC,∴MP=MQ,
又∠F=∠PCM,∴在Rt△PCM中,sin∠PCM=sinF=,
在Rt△BMQ中,sinB=,
∴=,④正确.
故选D.
【点评】本题考查了切线的性质,平行线的判定与性质,圆周角定理,相似三角形的判定与性质,角平分线的判定与性质,锐角三角函数的定义.关键是通过作辅助线,将问题转化到直角三角形中求解.
二.填空题(共4小题)
11.(2015 哈尔滨模拟)如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=,BD=2,则线段AE的长为 .
【分析】先求出∠DAB=∠E,证明△ABD∽△EAD,得出,即可求出AE=.
【解答】解:∵EA⊥AB,
∴∠EAB=90°,
∴∠B+∠E=90得,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD=,∠ADB=∠EAB,∠B+∠DAB=90°,
∴∠DAB=∠E,
∴△ABD∽△EAD,
∴∠DAB=∠E,
∴,,
∴AE=.
故答案为:.
【点评】本题考查了相似三角形的判定与性质;证明三角形相似得出比例式是解决问题的关键.
12.(2015 河南模拟)如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=,则PA的长为 1 .
【分析】根据已知可证△AOD为等边三角形,∠P=30°,PA=AD=OA,再证明PD是切线,根据切割线定理即可得出结果.
【解答】解:∵AB为直径,
∴∠ADB=90°,
∵∠BDE=60°,
∴∠PDA=180°﹣90°﹣60°=30°,
∴∠PBD=∠PDA=30°,
∵OB=OD,
∴∠ODB=∠PBD=30°,
∴∠ADO=60°,
∴△ADO为等边三角形,∠ODP=90°,
∴AD=OA,∠AOD=60°,PD为⊙O的切线,
∴∠P=30°,
∴PA=AD,PD2=PA PB,
∴(=PA 3PA
∴PA=1;
故答案为:1.
【点评】本题考查了圆周角定理、等边三角形的判定与性质、切线的判定与性质;证明三角形是等边三角形是解决问题的关键.
13.(2012秋 崇安区校级期末)如图,在△ABC中,AB=AC=5,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,sin∠CBF=,则BF的长为 .
【分析】因为AB为直径,所以连结AE,则可知过∠BAE=∠CBF,点C作CG∥BF,在Rt△ABE中可求得BE,进一步求得BC,在Rt△CGB中求出CG和GB,再利用平行线分线段成比例可求得.
【解答】解:连结AE,
∵AB是圆O的直径,
∴∠AEB=90°
∴∠1+∠2=90°
∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB,
∴∠1=∠CBF.
过点C作CG⊥AB于点G,
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1═,
∵∠AEB=90°,AB=5,
∴BE=AB sin∠1=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE=,
∴sin∠2=,cos∠2=,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴,
∴BF=.
故答案我:.
【点评】此题主要考查圆的有关性质及平行线分线段定理的应用,解题的关键是如何利用已知条件中的sin∠CBF=,属于中档题,有一定的难度.
14.(2010秋 北京校级期末)如图,△ABC内接于⊙O,AB是⊙O的直径,延长AB到D,连接CD.请你结合图形,编写一道题.要求:再补充两个已知条件,并写出在所有已知条件下得出的一个结论.例如:
“补充已知:OB=BD,CD切⊙O于点C,求证:∠A=∠D”
“补充已知: 条件:∠A=∠D,CD是⊙O的切线. .
求证: 结论:的度数为60° .”
【分析】添加∠A=∠D,CD是⊙O的切线,可以通过作辅助线OC,求出∠COB=90°,从而证出的度数为60°.
【解答】解:已知:∠A=∠D,CD是⊙O的切线,
求证:的度数为60°.
证明:连接OC,
则∠OCD=90°,
设∠A=∠ACO=∠D=x度,
在△ACO中,∠COD=2x度,
∴在直角三角形OCD中,2x+x=90,
解得x=30,
∴∠COD=60°.
【点评】本题是一道开放题,条件、结论、过程全开放,要有一定的知识积累方可正确解答.
三.解答题(共6小题)
15.(2016 新疆)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
【分析】(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)利用已知条件证得△AGC∽△ABF,利用比例式求得线段的长即可.
【解答】(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于G.
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=,
∵在Rt△AEB中,∠AEB=90°,AB=5,
∴BE=AB sin∠1=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE==2,
∴sin∠2===,cos∠2===,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴
∴BF==
【点评】本题考查常见的几何题型,包括切线的判定,角的大小及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.
16.(2016 天水)如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
【分析】(1)求证:MN是⊙O的切线,就可以证明∠NMC=90°
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,根据△NMC∽△BOC就可以求出MN的长.
【解答】(1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G
∴∠OBC=∠ABC,∠DCB=2∠DCM(1分)
∵AB∥CD
∴∠ABC+∠DCB=180°
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣90°=90°(2分)
∵MN∥OB
∴∠NMC=∠BOC=90°
即MN⊥MC
且MO是⊙O的半径
∴MN是⊙O的切线(4分)
(2)解:连接OF,则OF⊥BC(5分)
由(1)知,△BOC是直角三角形,
∴BC===10,
∵S△BOC= OB OC= BC OF
∴6×8=10×OF
∴0F=4.8cm
∴⊙O的半径为4.8cm(6分)
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°
∴△NMC∽△BOC(7分)
∴,即=,
∴MN=9.6(cm).(8分)
【点评】本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
17.(2016 西宁)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,.求BE的长.
【分析】(1)连OD,OE,根据圆周角定理得到∠ADO+∠ODB=90°,而∠CDA=∠CBD,∠CBD=∠ODB,于是∠CDA+∠ADO=90°;
(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
【解答】(1)证明:连结OD,
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
又∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∵OD是⊙O半径,
∴CD是⊙O的切线
(2)解:∵∠C=∠C,∠CDA=∠CBD
∴△CDA∽△CBD
∴
∵,BC=6,
∴CD=4,
∵CE,BE是⊙O的切线
∴BE=DE,BE⊥BC
∴BE2+BC2=EC2,即BE2+62=(4+BE)2
解得:BE=.
【点评】本题考查了切线的判定与性质:过半径的外端点与半径垂直的直线是圆的切线;也考查了圆周角定理的推论以及三角形相似的判定与性质.
18.(2016 永州)如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
【分析】(1)连接OC,由弦切角定理和切线的性质得出∠CBE=∠A,∠ABD=90°,由圆周角定理得出∠ACB=90°,得出∠ACO+∠BCO=90°,∠BCD=90°,由直角三角形斜边上的中线性质得出CE=BD=BE,得出∠BCE=∠CBE=∠A,证出∠ACO=∠BCE,得出∠BCE+∠BCO=90°,得出CE⊥OC,即可得出结论;
(2)由勾股定理求出AB,再由三角函数得出tanA===,求出BD=AB=,即可得出CE的长.
【解答】(1)证明:连接OC,如图所示:
∵BD是⊙O的切线,
∴∠CBE=∠A,∠ABD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,∠BCD=90°,
∵E是BD中点,
∴CE=BD=BE,
∴∠BCE=∠CBE=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴∠ACO=∠BCE,
∴∠BCE+∠BCO=90°,
即∠OCE=90°,CE⊥OC,
∴CE是⊙O的切线;
(2)解:∵∠ACB=90°,
∴AB===2,
∵tanA====,
∴BD=AB=,
∴CE=BD=.
【点评】本题考查了切线的判定、弦切角定理、圆周角定理、直角三角形斜边上的中线性质、勾股定理、三角函数等知识;熟练掌握切线的判定和圆周角定理是解决问题的关键.
19.(2016 贵港)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.
【分析】(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;
(2)根据余弦,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
【解答】(1)证明:如图1
,
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=,AB=12,得
OB=8.
由勾股定理,得
AO==4.
由三角形的面积,得
S△AOB=AB OE=OB AO,
OE==,
半圆O所在圆的半径是.
【点评】本题考查了切线的判定与性质,利用切线的判定是解题关键,利用面积相等得出关于OE的长是解题关键.
20.(2016 宁津县二模)如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=2,AD=2,求线段BC的长.
【分析】(1)因为BC经过圆的半径的外端,只要证明AB⊥BC即可.连接OE、OC,利用△OBC≌△OEC,得到∠OBC=90°即可证明BC为⊙O的切线.
(2)作DF⊥BC于点F,构造Rt△DFC,利用勾股定理解答即可.
【解答】(1)证明:连接OE、OC.
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
(2)解:过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2.
∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2)2,解得x=.
∴BC=.
【点评】此题考查了切线的判定和勾股定理的应用,作出辅助线构造直角三角形和全等三角形是解题的关键.
第1页(共1页)
