3.4.3去括号 课件
图片预览





文档简介
课件13张PPT。去 括 号(1)教学过程复习
1.化简:
(1)-(-2) (2) +(+1/2) (3) –(+3)
(4)+(-1/3) (5) -(-a) (6) +(-a)
上述化简有什么规律?
答案:(1)2 (2)1/2 (3) -3 (4) -1/3 (5) a (6) -a
2.在下列括号里填上适当的数。
(1) -2=( )?2
(2) -a=( )?a
(3) -(a-b)=( )?(a-b)
(1) -1 (2) -1 (3) -1
1. 加法的结合律:
a+(b+c)=a+b+c 2.若图书馆内原有a名同学。后来有些学生
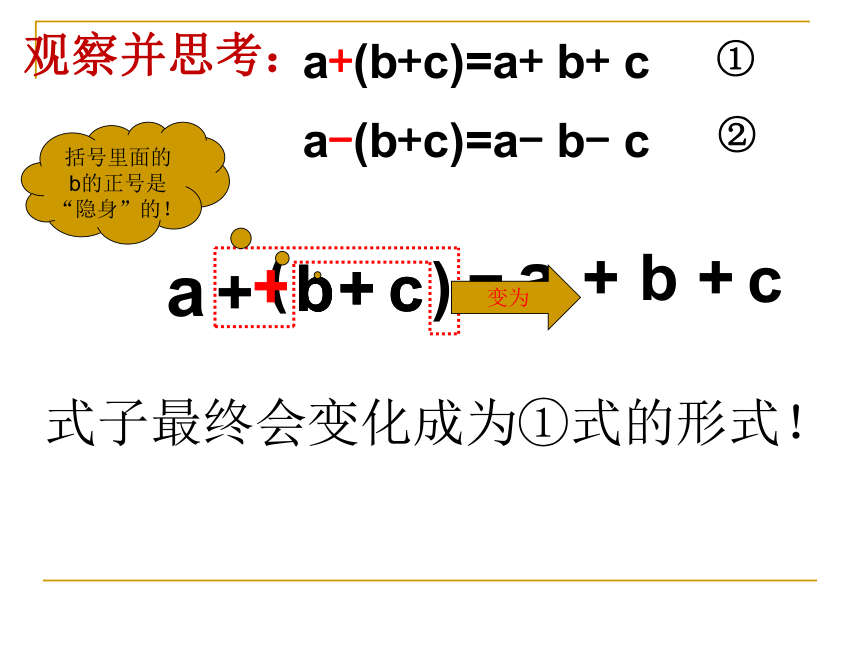
因上课要离开,第一批走了b位同学,第二批又走了c位同学。试用两种方式写出图书馆内还剩下的同学数?从中你能发现什么关系?a-(b+c)新知探究:a- b- c=a-(b+c)a- b- c思路一:(图书馆的总人数分别减去2次走的人数)思路二:(图书馆的总人数减去2次走的总人数)因此: a+(b+c)=a+ b+ c观察并思考:+b+c)(=b+bc+bac+ba+a-(b+c)=a- b- c①②+括号里面的b的正号是“隐身”的!变为式子最终会变化成为①式的形式!去括号法则 括号前是“+”号,把括号和它前面的“+”号去掉后,原来括号里各项的符号都不改变; 括号前是“-”号,把括号和它前面的“-”号去掉后,原来括号里各项的符号都要改变。
对去括号法则的理解及注意事项如下:(1)去括号的依据是乘法分配律;(2)注意法则中“都”字,变号时,各项都要变,不是只变第一项;若不变号,各项都不变号;(3)有多重括号时,一般先去小括号,再去中括号,最后去大括号。每去掉一层括号,如果有同类项应随时合并,为下一步运算简便化,减少差错。a-(b+c)=a- b- c;a+(b+c)=a+b+c;a+(b-c)=a+b-ca-(b-c)=a- b+ c都不变号:都变号:a(b+c)=ab+ac;a(b-c)=ab- ac例1 去括号: 1)a+(-b+c-d) 2)a-(-b+c-d) 3) a-3(-b+c-d)
解:(1)a+(-b+c-d) = a-b +c-d
(2)a-(-b+c-d) = a+b-c+d
(3)a-3(-b+c-d)
= a-(-3b+3c-3d)
= a+3b -3c+3d(含数乘)(乘法分配率)(去括号) 比一比,看谁快又准确率高 !1.去括号:(1)-(1-3x)=(2)2(x2-3x)=(3)-3 (x2-1)=-1+3x2x2-6x-3 x2+3 去括号,再合并同类项 (5a-3b) -3(a-2b)解:原式= 5a-3b-(3 a-6b)
= 5a-3b- 3 a+6b
=2a+3b 练一练:将3先乘入括号,再按
去括号法则去括号例2 先去括号,再合并同类项: (1)8a+2b+(5a-b); (2)6a+2(a-c).
解: (1)8a+2b+(5a-b)
= 8a+2b+ 5a-b ——不用变号
=13a+b ——合并同类项
(2)6a+2(a-c)
= 6a+(2a-2c) ——乘法分配律
=6a+2a-2c ———去括号
=8a-2c ——合并同类项 我来试 ③ 代数式去括号后,都必须经过合并同类项,其结果才能简洁。去括号并合并同类项:(1)(2)(3)解:(1)4a-(a-3b)(2)原式=(3)原式②括号前是否有数乘注意:① 是否变号=4a a -3b-+(依据是什么?)(依据是什么?)(去括号法则)(合并同类项法则)=6xy-3y-2xya+5a-3b-(2a-4b)随堂检测:1.口答:去括号
(1)a + (– b + c ) =
( 2 ) ( a – b ) – 2( c + d ) =
( 3 ) – (– a + b ) – c =
( 4 ) – (2x – y ) – ( - x2 + y2 ) =
2.判断下列计算是否正确,错的请说明理由:( )( )( )( )提高问题:
去括号- { - [ - ( a – 2 b ) ] }解法一:原式= - [-(- a+2b) ]
= - (a -2b)
= -a + 2b解法二:将a-2b看成一个整体,运用多重符号的
化简方法。
原式= -(a-2b)
=-a+2b
1.化简:
(1)-(-2) (2) +(+1/2) (3) –(+3)
(4)+(-1/3) (5) -(-a) (6) +(-a)
上述化简有什么规律?
答案:(1)2 (2)1/2 (3) -3 (4) -1/3 (5) a (6) -a
2.在下列括号里填上适当的数。
(1) -2=( )?2
(2) -a=( )?a
(3) -(a-b)=( )?(a-b)
(1) -1 (2) -1 (3) -1
1. 加法的结合律:
a+(b+c)=a+b+c 2.若图书馆内原有a名同学。后来有些学生
因上课要离开,第一批走了b位同学,第二批又走了c位同学。试用两种方式写出图书馆内还剩下的同学数?从中你能发现什么关系?a-(b+c)新知探究:a- b- c=a-(b+c)a- b- c思路一:(图书馆的总人数分别减去2次走的人数)思路二:(图书馆的总人数减去2次走的总人数)因此: a+(b+c)=a+ b+ c观察并思考:+b+c)(=b+bc+bac+ba+a-(b+c)=a- b- c①②+括号里面的b的正号是“隐身”的!变为式子最终会变化成为①式的形式!去括号法则 括号前是“+”号,把括号和它前面的“+”号去掉后,原来括号里各项的符号都不改变; 括号前是“-”号,把括号和它前面的“-”号去掉后,原来括号里各项的符号都要改变。
对去括号法则的理解及注意事项如下:(1)去括号的依据是乘法分配律;(2)注意法则中“都”字,变号时,各项都要变,不是只变第一项;若不变号,各项都不变号;(3)有多重括号时,一般先去小括号,再去中括号,最后去大括号。每去掉一层括号,如果有同类项应随时合并,为下一步运算简便化,减少差错。a-(b+c)=a- b- c;a+(b+c)=a+b+c;a+(b-c)=a+b-ca-(b-c)=a- b+ c都不变号:都变号:a(b+c)=ab+ac;a(b-c)=ab- ac例1 去括号: 1)a+(-b+c-d) 2)a-(-b+c-d) 3) a-3(-b+c-d)
解:(1)a+(-b+c-d) = a-b +c-d
(2)a-(-b+c-d) = a+b-c+d
(3)a-3(-b+c-d)
= a-(-3b+3c-3d)
= a+3b -3c+3d(含数乘)(乘法分配率)(去括号) 比一比,看谁快又准确率高 !1.去括号:(1)-(1-3x)=(2)2(x2-3x)=(3)-3 (x2-1)=-1+3x2x2-6x-3 x2+3 去括号,再合并同类项 (5a-3b) -3(a-2b)解:原式= 5a-3b-(3 a-6b)
= 5a-3b- 3 a+6b
=2a+3b 练一练:将3先乘入括号,再按
去括号法则去括号例2 先去括号,再合并同类项: (1)8a+2b+(5a-b); (2)6a+2(a-c).
解: (1)8a+2b+(5a-b)
= 8a+2b+ 5a-b ——不用变号
=13a+b ——合并同类项
(2)6a+2(a-c)
= 6a+(2a-2c) ——乘法分配律
=6a+2a-2c ———去括号
=8a-2c ——合并同类项 我来试 ③ 代数式去括号后,都必须经过合并同类项,其结果才能简洁。去括号并合并同类项:(1)(2)(3)解:(1)4a-(a-3b)(2)原式=(3)原式②括号前是否有数乘注意:① 是否变号=4a a -3b-+(依据是什么?)(依据是什么?)(去括号法则)(合并同类项法则)=6xy-3y-2xya+5a-3b-(2a-4b)随堂检测:1.口答:去括号
(1)a + (– b + c ) =
( 2 ) ( a – b ) – 2( c + d ) =
( 3 ) – (– a + b ) – c =
( 4 ) – (2x – y ) – ( - x2 + y2 ) =
2.判断下列计算是否正确,错的请说明理由:( )( )( )( )提高问题:
去括号- { - [ - ( a – 2 b ) ] }解法一:原式= - [-(- a+2b) ]
= - (a -2b)
= -a + 2b解法二:将a-2b看成一个整体,运用多重符号的
化简方法。
原式= -(a-2b)
=-a+2b
