吉林省松原市油田高中2015-2016学年高二(下)开学数学试卷(理科)(解析版)
文档属性
| 名称 | 吉林省松原市油田高中2015-2016学年高二(下)开学数学试卷(理科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-08 15:33:03 | ||
图片预览




文档简介
2015-2016学年吉林省松原市油田高中高二(下)开学数学试卷(理科)
一、选择题:(本大题共12小题,每题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设a<b<0,下列不等式一定成立的是( )
A.a2<ab<b2
B.b2<ab<a2
C.a2<b2<ab
D.ab<b2<a2
2.设P是椭圆上一点,F1、F2是椭圆的焦点,若|PF1|等于4,则|PF2|等于( )
A.22
B.21
C.20
D.13
3.下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
B.若命题p: x∈R,x2﹣2x﹣1>0,则命题 p: x∈R,x2﹣2x﹣1<0
C.命题“若x=y,则sinx=siny”的逆否命题为真命题
D.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件
4.已知双曲线的中心为原点,F(3,0)是双曲线的﹣个焦点,是双曲线的一条渐近线,则双曲线的标准方程为( )
A.
B.
C.
D.
5.已知等差数列{an}的公差为2,若a1,a3和a4成等比数列,则a1可以等于( )
A.﹣4
B.﹣6
C.﹣8
D.﹣10
6.已知命题p: x∈R,cosx=2;命题q: x∈R,x2﹣x+1>0,则下列结论中正确的是( )
A.p∨q是假命题
B.p∧q是真命题
C.(¬p)∧(¬q)是真命题
D.(¬p)∨(¬q)是真命题
7.设D为△ABC所在平面内一点,,则( )
A.
B.
C.
D.
8.
=( )
A.
B.
C.
D.
9.若x,y满足约束条件,则的最大值为( )
A.2
B.
C.3
D.1
10.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.
B.
C.
D.
11.已知空间四个点A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),则直线AD与平面ABC所成的角为( )
A.30°
B.45°
C.60°
D.90°
12.已知M(x0,y0)是双曲线C:
=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是( )
A.
B.
C.
D.
二、填空题(共4小题,每小题4分,满分16分)
13.若且,则实数λ的值是______.
14.若正实数x,y满足2x+y+6=xy,则xy的最小值是______.
15.在△ABC中,a=3,b=,∠A=,则∠B=______.
16.已知以F为焦点的抛物线y2=4x上的两点A、B满足=3,则弦AB的中点到准线的距离为______.
三、解答题:(本大题共4小题,共36分,其中17、18题各8分,19、20题各10分解答应写出文字说明,证明过程或演算步骤.)
17.在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,.
(1)若△ABC的面积等于,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
18.等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2+n,求b1+b2+b3+…+b10的值.
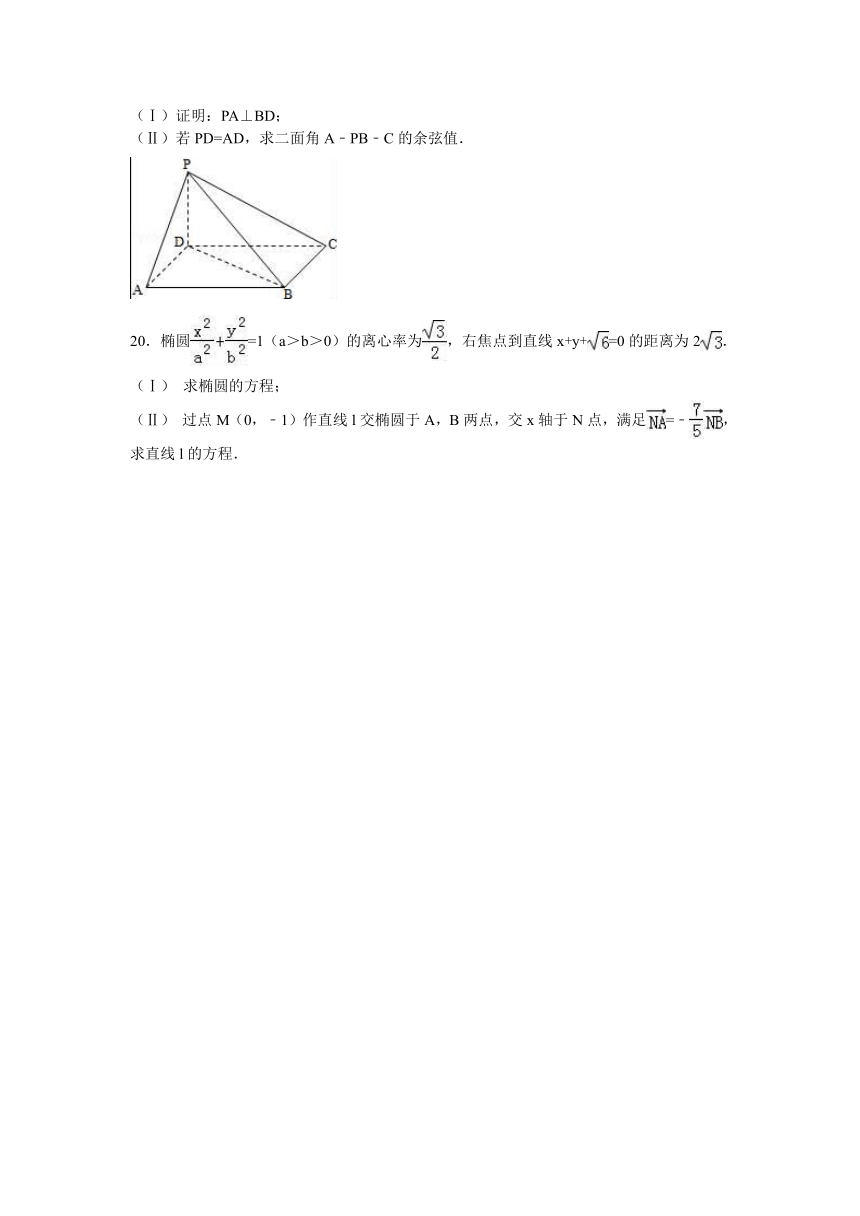
19.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.
20.椭圆=1(a>b>0)的离心率为,右焦点到直线x+y+=0的距离为2.
(Ⅰ)
求椭圆的方程;
(Ⅱ)
过点M(0,﹣1)作直线l交椭圆于A,B两点,交x轴于N点,满足=﹣,求直线l的方程.
2015-2016学年吉林省松原市油田高中高二(下)开学数学试卷(理科)
参考答案与试题解析
一、选择题:(本大题共12小题,每题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设a<b<0,下列不等式一定成立的是( )
A.a2<ab<b2
B.b2<ab<a2
C.a2<b2<ab
D.ab<b2<a2
【考点】不等式的基本性质.
【分析】利用不等式的基本性质即可得出.
【解答】解:∵a<b<0,
∴a2>ab,ab>b2,
即a2>ab>b2,
故选:B.
2.设P是椭圆上一点,F1、F2是椭圆的焦点,若|PF1|等于4,则|PF2|等于( )
A.22
B.21
C.20
D.13
【考点】椭圆的简单性质.
【分析】由已知条件,利用|PF1|+|PF2|=2a,能求出结果.
【解答】解:∵P是椭圆上一点,
F1、F2是椭圆的焦点,|PF1|等于4,
∴|PF2|=2﹣|PF1|=26﹣4=22.
故选A.
3.下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
B.若命题p: x∈R,x2﹣2x﹣1>0,则命题 p: x∈R,x2﹣2x﹣1<0
C.命题“若x=y,则sinx=siny”的逆否命题为真命题
D.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件
【考点】四种命题.
【分析】A,写出它的否命题,即可判定真假;
B,写出命题p的否定¬p;
C,判定原命题的真假性,即可得出它的逆否命题的真假性;
D,由“x=﹣1”得出“x2﹣5x﹣6=0”成立,判定命题是否正确.
【解答】解:对于A,否命题是“若x2≠1,则x≠1”,∴A错误;
对于B,命题p的否定¬p: x∈R,x2﹣2x﹣1≤0,∴B错误;
对于C,命题“若x=y,则sinx=siny”是真命题,∴它的逆否命题是真命题,∴C正确;
对于D,“x=﹣1”时,“x2﹣5x﹣6=0”,∴是充分条件,∴D错误;
故选:C.
4.已知双曲线的中心为原点,F(3,0)是双曲线的﹣个焦点,是双曲线的一条渐近线,则双曲线的标准方程为( )
A.
B.
C.
D.
【考点】双曲线的简单性质.
【分析】根据已知条件,利用双曲线的焦点坐标,设出双曲线的标准方程,再由双曲线的渐近线方程,求出双曲线的标准方程.
【解答】解:∵双曲线的中心为原点,F(3,0)是双曲线的﹣个焦点,
∴设双曲线方程为,a>0,
∵是双曲线的一条渐近线,
∴=,解得a2=4,
∴双曲线方程为.
故选D.
5.已知等差数列{an}的公差为2,若a1,a3和a4成等比数列,则a1可以等于( )
A.﹣4
B.﹣6
C.﹣8
D.﹣10
【考点】等差数列的性质.
【分析】依题意,(a1+2d)2=a1 (a1+3d),可求得a1.
【解答】解:∵等差数列{an}的公差d=2,a1,a3和a4成等比数列,
∴(a1+2d)2=a1 (a1+3d),
∴a1d+4d2=0,∴a1=﹣8,
故选:C.
6.已知命题p: x∈R,cosx=2;命题q: x∈R,x2﹣x+1>0,则下列结论中正确的是( )
A.p∨q是假命题
B.p∧q是真命题
C.(¬p)∧(¬q)是真命题
D.(¬p)∨(¬q)是真命题
【考点】复合命题的真假.
【分析】利用余弦函数的性质说明命题p为真命题,利用配方法求得x2﹣x+1的范围,说明命题q为假命题,然后利用符合命题的真值表加以判断即可得到答案.
【解答】解:由x2﹣x+1=(x﹣)2+>0,所以命题q: x∈R,x2﹣x+1>0,为真命题;
由cosx≤1,可知命题p: x∈R,cosx=2是假命题.
故由以上可知:
¬p是真命题;q是真命题;pⅤq是真命题;命题“p∧q”是假命题;命题(¬p)∨(¬q)是真命题.
故选:D.
7.设D为△ABC所在平面内一点,,则( )
A.
B.
C.
D.
【考点】平行向量与共线向量.
【分析】将向量利用向量的三角形法则首先表示为,然后结合已知表示为的形式.
【解答】解:由已知得到如图
由===;
故选:A.
8.
=( )
A.
B.
C.
D.
【考点】数列的求和.
【分析】根据分式的性质,有=(1﹣),=(﹣),…=(﹣)成立,则可得原式=(1﹣)+(﹣)+…+(﹣),化简可得答案.
【解答】解:原式=(1﹣)+(﹣)+…+(﹣)=
[(1﹣)+(﹣)+…+(﹣)]=(1﹣)=;
故选A.
9.若x,y满足约束条件,则的最大值为( )
A.2
B.
C.3
D.1
【考点】简单线性规划.
【分析】由约束条件作出可行域,由的几何意义,即可行域内的动点与定点M(0,1)连线的斜率求得答案.
【解答】解:由约束条件作出可行域如图,
的几何意义为可行域内的动点与定点M(0,1)连线的斜率,
联立,解得A(﹣1,﹣1),
∴的最大值为.
故选:A.
10.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.
B.
C.
D.
【考点】椭圆的标准方程.
【分析】设A(x1,y1),B(x2,y2),代入椭圆方程得,利用“点差法”可得.利用中点坐标公式可得x1+x2=2,y1+y2=﹣2,利用斜率计算公式可得==.于是得到,化为a2=2b2,再利用c=3=,即可解得a2,b2.进而得到椭圆的方程.
【解答】解:设A(x1,y1),B(x2,y2),
代入椭圆方程得,
相减得,
∴.
∵x1+x2=2,y1+y2=﹣2,
==.
∴,
化为a2=2b2,又c=3=,解得a2=18,b2=9.
∴椭圆E的方程为.
故选D.
11.已知空间四个点A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),则直线AD与平面ABC所成的角为( )
A.30°
B.45°
C.60°
D.90°
【考点】直线与平面所成的角.
【分析】利用已知条件,分别求出向量和平面ABC的法向量,利用向量法能求出结果.
【解答】解:∵A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),
∴=(﹣2,﹣1,3),(﹣5,﹣1,1),=(﹣4,﹣2,﹣1),
设平面ABC的法向量为,
则,,
∴,
∴﹣9x﹣3y=0,
令x=1,得y=﹣3,z=2,∴,
设直线AD与平面ABC所成的角为θ,
则sinθ=|cos<>|=||=,
∴θ=30°.
故选:A.
12.已知M(x0,y0)是双曲线C:
=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是( )
A.
B.
C.
D.
【考点】双曲线的简单性质.
【分析】利用向量的数量积公式,结合双曲线方程,即可确定y0的取值范围.
【解答】解:由题意,
=(﹣x0,﹣y0) (﹣﹣x0,﹣y0)=x02﹣3+y02=3y02﹣1<0,
所以﹣<y0<.
故选:A.
二、填空题(共4小题,每小题4分,满分16分)
13.若且,则实数λ的值是 ﹣2 .
【考点】向量的数量积判断向量的共线与垂直.
【分析】根据已知求出向量=(λ,1+λ,﹣1),再利用向量垂直的条件即可求出λ的值.
【解答】解:∵,
∴=(λ,1+λ,﹣1),
又∵,
∴()=0.
∴(λ,1+λ,﹣1) (0,1,﹣1)=0.
即1+λ+1=0.
∴λ=﹣2.
故答案为:﹣2.
14.若正实数x,y满足2x+y+6=xy,则xy的最小值是 18 .
【考点】基本不等式.
【分析】首先左边是xy的形式右边是2x+y和常数的和的形式,考虑把右边也转化成xy的形式,使形式统一.可以猜想到应用基本不等式.转化后变成关于xy的方程,可把xy看成整体换元后求最小值.
【解答】解:由条件利用基本不等式可得,
令xy=t2,即
t=>0,可得.
即得到可解得.
又注意到t>0,故解为,
所以xy≥18.
故答案应为18.
15.在△ABC中,a=3,b=,∠A=,则∠B= .
【考点】正弦定理.
【分析】由正弦定理可得sinB,再由三角形的边角关系,即可得到角B.
【解答】解:由正弦定理可得,
=,
即有sinB===,
由b<a,则B<A,
可得B=.
故答案为:.
16.已知以F为焦点的抛物线y2=4x上的两点A、B满足=3,则弦AB的中点到准线的距离为 .
【考点】抛物线的简单性质;点到直线的距离公式;抛物线的定义.
【分析】设BF=m,由抛物线的定义知AA1和BB1,进而可推断出AC和AB,及直线AB的斜率,则直线AB的方程可得,与抛物线方程联立消去y,进而跟韦达定理求得x1+x2的值,则根据抛物线的定义求得弦AB的中点到准线的距离.
【解答】解:设BF=m,由抛物线的定义知
AA1=3m,BB1=m
∴△ABC中,AC=2m,AB=4m,
直线AB方程为
与抛物线方程联立消y得3x2﹣10x+3=0
所以AB中点到准线距离为
故答案为
三、解答题:(本大题共4小题,共36分,其中17、18题各8分,19、20题各10分解答应写出文字说明,证明过程或演算步骤.)
17.在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,.
(1)若△ABC的面积等于,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
【考点】解三角形;三角形中的几何计算.
【分析】(1)由c及cosC的值,利用余弦定理列出关于a与b的关系式a2+b2﹣ab=4,再由已知三角形的面积及sinC的值,利用三角形的面积公式得出ab的值,与a2+b2﹣ab=4联立组成方程组,求出方程组的解即可求出a与b的值;
(2)利用正弦定理化简sinB=2sinA,得到b=2a,与(1)得出的a2+b2﹣ab=4联立组成方程组,求出方程组的解得到a与b的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
【解答】解:(1)∵c=2,cosC=,
∴由余弦定理c2=a2+b2﹣2abcosC得:a2+b2﹣ab=4,
又△ABC的面积等于,sinC=,
∴,
整理得:ab=4,
联立方程组,
解得a=2,b=2;
(2)由正弦定理,把sinB=2sinA化为b=2a,
联立方程组,
解得:,,
又sinC=,
则△ABC的面积.
18.等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2+n,求b1+b2+b3+…+b10的值.
【考点】等差数列的性质.
【分析】(Ⅰ)建立方程组求出首项与公差,即可求数列{an}的通项公式;
(Ⅱ)bn=2+n=2n+n,利用分组求和求b1+b2+b3+…+b10的值.
【解答】解:(Ⅰ)设公差为d,则,
解得,
所以an=3+(n﹣1)=n+2;
(Ⅱ)bn=2+n=2n+n,
所以b1+b2+b3+…+b10=(2+1)+(22+2)+…+
=(2+22+…+210)+(1+2+…+10)
=+=2101.
19.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.
【考点】直线与平面垂直的性质;用空间向量求平面间的夹角.
【分析】(Ⅰ)因为∠DAB=60°,AB=2AD,由余弦定理得BD=,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;
(Ⅱ)建立空间直角坐标系,写出点A,B,C,P的坐标,求出向量,和平面PAB的法向量,平面PBC的法向量,求出这两个向量的夹角的余弦值即可.
【解答】(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=,
从而BD2+AD2=AB2,故BD⊥AD
又PD⊥底面ABCD,可得BD⊥PD
所以BD⊥平面PAD.故PA⊥BD
(Ⅱ)如图,以D为坐标原点,AD的长为单位长,
射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz,则
A(1,0,0),B(0,,0),C(﹣1,,0),P(0,0,1).
=(﹣1,,0),=(0,,﹣1),=(﹣1,0,0),
设平面PAB的法向量为=(x,y,z),则
即,
因此可取=(,1,)
设平面PBC的法向量为=(x,y,z),则,
即:
可取=(0,1,),cos<>==
故二面角A﹣PB﹣C的余弦值为:﹣.
20.椭圆=1(a>b>0)的离心率为,右焦点到直线x+y+=0的距离为2.
(Ⅰ)
求椭圆的方程;
(Ⅱ)
过点M(0,﹣1)作直线l交椭圆于A,B两点,交x轴于N点,满足=﹣,求直线l的方程.
【考点】直线与圆锥曲线的综合问题.
【分析】(Ⅰ)根据圆的离心率为,右焦点到直线x+y+=0的距离为2,建立方程组,可求椭圆的方程;
(Ⅱ)设A
(x1,y1),B(x2,y2),N(x0,0),利用=﹣,可得(x1﹣x0,y1)=﹣(x2﹣x0,y2),设直线l的方程为y=kx﹣1(k≠0),与椭圆方程联立,消去x可得(4k2+1)y2+2y+1﹣8k2=0,由此即可求得直线l的方程.
【解答】解:(Ⅰ)∵椭圆的离心率为,右焦点到直线x+y+=0的距离为2,
∴
∴c=,a=2,
∴b=,
∴椭圆的方程为;
(Ⅱ)设A
(x1,y1),B(x2,y2),N(x0,0)
∵=﹣,
∴(x1﹣x0,y1)=﹣(x2﹣x0,y2)
∴y1=﹣y2①
易知直线斜率不存在时或斜率为0时①不成立
于是设直线l的方程为y=kx﹣1(k≠0).
与椭圆方程联立,消去x可得(4k2+1)y2+2y+1﹣8k2=0②
∴y1+y2=﹣③y1y2=④
由①③可得y2=,y1=﹣代入④整理可得:8k4+k2﹣9=0
∴k2=1
此时②为5y2+2y﹣7=0,判别式大于0
∴直线l的方程为y=±x﹣1.
2016年10月8日
一、选择题:(本大题共12小题,每题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设a<b<0,下列不等式一定成立的是( )
A.a2<ab<b2
B.b2<ab<a2
C.a2<b2<ab
D.ab<b2<a2
2.设P是椭圆上一点,F1、F2是椭圆的焦点,若|PF1|等于4,则|PF2|等于( )
A.22
B.21
C.20
D.13
3.下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
B.若命题p: x∈R,x2﹣2x﹣1>0,则命题 p: x∈R,x2﹣2x﹣1<0
C.命题“若x=y,则sinx=siny”的逆否命题为真命题
D.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件
4.已知双曲线的中心为原点,F(3,0)是双曲线的﹣个焦点,是双曲线的一条渐近线,则双曲线的标准方程为( )
A.
B.
C.
D.
5.已知等差数列{an}的公差为2,若a1,a3和a4成等比数列,则a1可以等于( )
A.﹣4
B.﹣6
C.﹣8
D.﹣10
6.已知命题p: x∈R,cosx=2;命题q: x∈R,x2﹣x+1>0,则下列结论中正确的是( )
A.p∨q是假命题
B.p∧q是真命题
C.(¬p)∧(¬q)是真命题
D.(¬p)∨(¬q)是真命题
7.设D为△ABC所在平面内一点,,则( )
A.
B.
C.
D.
8.
=( )
A.
B.
C.
D.
9.若x,y满足约束条件,则的最大值为( )
A.2
B.
C.3
D.1
10.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.
B.
C.
D.
11.已知空间四个点A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),则直线AD与平面ABC所成的角为( )
A.30°
B.45°
C.60°
D.90°
12.已知M(x0,y0)是双曲线C:
=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是( )
A.
B.
C.
D.
二、填空题(共4小题,每小题4分,满分16分)
13.若且,则实数λ的值是______.
14.若正实数x,y满足2x+y+6=xy,则xy的最小值是______.
15.在△ABC中,a=3,b=,∠A=,则∠B=______.
16.已知以F为焦点的抛物线y2=4x上的两点A、B满足=3,则弦AB的中点到准线的距离为______.
三、解答题:(本大题共4小题,共36分,其中17、18题各8分,19、20题各10分解答应写出文字说明,证明过程或演算步骤.)
17.在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,.
(1)若△ABC的面积等于,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
18.等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2+n,求b1+b2+b3+…+b10的值.
19.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.
20.椭圆=1(a>b>0)的离心率为,右焦点到直线x+y+=0的距离为2.
(Ⅰ)
求椭圆的方程;
(Ⅱ)
过点M(0,﹣1)作直线l交椭圆于A,B两点,交x轴于N点,满足=﹣,求直线l的方程.
2015-2016学年吉林省松原市油田高中高二(下)开学数学试卷(理科)
参考答案与试题解析
一、选择题:(本大题共12小题,每题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设a<b<0,下列不等式一定成立的是( )
A.a2<ab<b2
B.b2<ab<a2
C.a2<b2<ab
D.ab<b2<a2
【考点】不等式的基本性质.
【分析】利用不等式的基本性质即可得出.
【解答】解:∵a<b<0,
∴a2>ab,ab>b2,
即a2>ab>b2,
故选:B.
2.设P是椭圆上一点,F1、F2是椭圆的焦点,若|PF1|等于4,则|PF2|等于( )
A.22
B.21
C.20
D.13
【考点】椭圆的简单性质.
【分析】由已知条件,利用|PF1|+|PF2|=2a,能求出结果.
【解答】解:∵P是椭圆上一点,
F1、F2是椭圆的焦点,|PF1|等于4,
∴|PF2|=2﹣|PF1|=26﹣4=22.
故选A.
3.下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
B.若命题p: x∈R,x2﹣2x﹣1>0,则命题 p: x∈R,x2﹣2x﹣1<0
C.命题“若x=y,则sinx=siny”的逆否命题为真命题
D.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件
【考点】四种命题.
【分析】A,写出它的否命题,即可判定真假;
B,写出命题p的否定¬p;
C,判定原命题的真假性,即可得出它的逆否命题的真假性;
D,由“x=﹣1”得出“x2﹣5x﹣6=0”成立,判定命题是否正确.
【解答】解:对于A,否命题是“若x2≠1,则x≠1”,∴A错误;
对于B,命题p的否定¬p: x∈R,x2﹣2x﹣1≤0,∴B错误;
对于C,命题“若x=y,则sinx=siny”是真命题,∴它的逆否命题是真命题,∴C正确;
对于D,“x=﹣1”时,“x2﹣5x﹣6=0”,∴是充分条件,∴D错误;
故选:C.
4.已知双曲线的中心为原点,F(3,0)是双曲线的﹣个焦点,是双曲线的一条渐近线,则双曲线的标准方程为( )
A.
B.
C.
D.
【考点】双曲线的简单性质.
【分析】根据已知条件,利用双曲线的焦点坐标,设出双曲线的标准方程,再由双曲线的渐近线方程,求出双曲线的标准方程.
【解答】解:∵双曲线的中心为原点,F(3,0)是双曲线的﹣个焦点,
∴设双曲线方程为,a>0,
∵是双曲线的一条渐近线,
∴=,解得a2=4,
∴双曲线方程为.
故选D.
5.已知等差数列{an}的公差为2,若a1,a3和a4成等比数列,则a1可以等于( )
A.﹣4
B.﹣6
C.﹣8
D.﹣10
【考点】等差数列的性质.
【分析】依题意,(a1+2d)2=a1 (a1+3d),可求得a1.
【解答】解:∵等差数列{an}的公差d=2,a1,a3和a4成等比数列,
∴(a1+2d)2=a1 (a1+3d),
∴a1d+4d2=0,∴a1=﹣8,
故选:C.
6.已知命题p: x∈R,cosx=2;命题q: x∈R,x2﹣x+1>0,则下列结论中正确的是( )
A.p∨q是假命题
B.p∧q是真命题
C.(¬p)∧(¬q)是真命题
D.(¬p)∨(¬q)是真命题
【考点】复合命题的真假.
【分析】利用余弦函数的性质说明命题p为真命题,利用配方法求得x2﹣x+1的范围,说明命题q为假命题,然后利用符合命题的真值表加以判断即可得到答案.
【解答】解:由x2﹣x+1=(x﹣)2+>0,所以命题q: x∈R,x2﹣x+1>0,为真命题;
由cosx≤1,可知命题p: x∈R,cosx=2是假命题.
故由以上可知:
¬p是真命题;q是真命题;pⅤq是真命题;命题“p∧q”是假命题;命题(¬p)∨(¬q)是真命题.
故选:D.
7.设D为△ABC所在平面内一点,,则( )
A.
B.
C.
D.
【考点】平行向量与共线向量.
【分析】将向量利用向量的三角形法则首先表示为,然后结合已知表示为的形式.
【解答】解:由已知得到如图
由===;
故选:A.
8.
=( )
A.
B.
C.
D.
【考点】数列的求和.
【分析】根据分式的性质,有=(1﹣),=(﹣),…=(﹣)成立,则可得原式=(1﹣)+(﹣)+…+(﹣),化简可得答案.
【解答】解:原式=(1﹣)+(﹣)+…+(﹣)=
[(1﹣)+(﹣)+…+(﹣)]=(1﹣)=;
故选A.
9.若x,y满足约束条件,则的最大值为( )
A.2
B.
C.3
D.1
【考点】简单线性规划.
【分析】由约束条件作出可行域,由的几何意义,即可行域内的动点与定点M(0,1)连线的斜率求得答案.
【解答】解:由约束条件作出可行域如图,
的几何意义为可行域内的动点与定点M(0,1)连线的斜率,
联立,解得A(﹣1,﹣1),
∴的最大值为.
故选:A.
10.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.
B.
C.
D.
【考点】椭圆的标准方程.
【分析】设A(x1,y1),B(x2,y2),代入椭圆方程得,利用“点差法”可得.利用中点坐标公式可得x1+x2=2,y1+y2=﹣2,利用斜率计算公式可得==.于是得到,化为a2=2b2,再利用c=3=,即可解得a2,b2.进而得到椭圆的方程.
【解答】解:设A(x1,y1),B(x2,y2),
代入椭圆方程得,
相减得,
∴.
∵x1+x2=2,y1+y2=﹣2,
==.
∴,
化为a2=2b2,又c=3=,解得a2=18,b2=9.
∴椭圆E的方程为.
故选D.
11.已知空间四个点A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),则直线AD与平面ABC所成的角为( )
A.30°
B.45°
C.60°
D.90°
【考点】直线与平面所成的角.
【分析】利用已知条件,分别求出向量和平面ABC的法向量,利用向量法能求出结果.
【解答】解:∵A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),
∴=(﹣2,﹣1,3),(﹣5,﹣1,1),=(﹣4,﹣2,﹣1),
设平面ABC的法向量为,
则,,
∴,
∴﹣9x﹣3y=0,
令x=1,得y=﹣3,z=2,∴,
设直线AD与平面ABC所成的角为θ,
则sinθ=|cos<>|=||=,
∴θ=30°.
故选:A.
12.已知M(x0,y0)是双曲线C:
=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是( )
A.
B.
C.
D.
【考点】双曲线的简单性质.
【分析】利用向量的数量积公式,结合双曲线方程,即可确定y0的取值范围.
【解答】解:由题意,
=(﹣x0,﹣y0) (﹣﹣x0,﹣y0)=x02﹣3+y02=3y02﹣1<0,
所以﹣<y0<.
故选:A.
二、填空题(共4小题,每小题4分,满分16分)
13.若且,则实数λ的值是 ﹣2 .
【考点】向量的数量积判断向量的共线与垂直.
【分析】根据已知求出向量=(λ,1+λ,﹣1),再利用向量垂直的条件即可求出λ的值.
【解答】解:∵,
∴=(λ,1+λ,﹣1),
又∵,
∴()=0.
∴(λ,1+λ,﹣1) (0,1,﹣1)=0.
即1+λ+1=0.
∴λ=﹣2.
故答案为:﹣2.
14.若正实数x,y满足2x+y+6=xy,则xy的最小值是 18 .
【考点】基本不等式.
【分析】首先左边是xy的形式右边是2x+y和常数的和的形式,考虑把右边也转化成xy的形式,使形式统一.可以猜想到应用基本不等式.转化后变成关于xy的方程,可把xy看成整体换元后求最小值.
【解答】解:由条件利用基本不等式可得,
令xy=t2,即
t=>0,可得.
即得到可解得.
又注意到t>0,故解为,
所以xy≥18.
故答案应为18.
15.在△ABC中,a=3,b=,∠A=,则∠B= .
【考点】正弦定理.
【分析】由正弦定理可得sinB,再由三角形的边角关系,即可得到角B.
【解答】解:由正弦定理可得,
=,
即有sinB===,
由b<a,则B<A,
可得B=.
故答案为:.
16.已知以F为焦点的抛物线y2=4x上的两点A、B满足=3,则弦AB的中点到准线的距离为 .
【考点】抛物线的简单性质;点到直线的距离公式;抛物线的定义.
【分析】设BF=m,由抛物线的定义知AA1和BB1,进而可推断出AC和AB,及直线AB的斜率,则直线AB的方程可得,与抛物线方程联立消去y,进而跟韦达定理求得x1+x2的值,则根据抛物线的定义求得弦AB的中点到准线的距离.
【解答】解:设BF=m,由抛物线的定义知
AA1=3m,BB1=m
∴△ABC中,AC=2m,AB=4m,
直线AB方程为
与抛物线方程联立消y得3x2﹣10x+3=0
所以AB中点到准线距离为
故答案为
三、解答题:(本大题共4小题,共36分,其中17、18题各8分,19、20题各10分解答应写出文字说明,证明过程或演算步骤.)
17.在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,.
(1)若△ABC的面积等于,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
【考点】解三角形;三角形中的几何计算.
【分析】(1)由c及cosC的值,利用余弦定理列出关于a与b的关系式a2+b2﹣ab=4,再由已知三角形的面积及sinC的值,利用三角形的面积公式得出ab的值,与a2+b2﹣ab=4联立组成方程组,求出方程组的解即可求出a与b的值;
(2)利用正弦定理化简sinB=2sinA,得到b=2a,与(1)得出的a2+b2﹣ab=4联立组成方程组,求出方程组的解得到a与b的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
【解答】解:(1)∵c=2,cosC=,
∴由余弦定理c2=a2+b2﹣2abcosC得:a2+b2﹣ab=4,
又△ABC的面积等于,sinC=,
∴,
整理得:ab=4,
联立方程组,
解得a=2,b=2;
(2)由正弦定理,把sinB=2sinA化为b=2a,
联立方程组,
解得:,,
又sinC=,
则△ABC的面积.
18.等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2+n,求b1+b2+b3+…+b10的值.
【考点】等差数列的性质.
【分析】(Ⅰ)建立方程组求出首项与公差,即可求数列{an}的通项公式;
(Ⅱ)bn=2+n=2n+n,利用分组求和求b1+b2+b3+…+b10的值.
【解答】解:(Ⅰ)设公差为d,则,
解得,
所以an=3+(n﹣1)=n+2;
(Ⅱ)bn=2+n=2n+n,
所以b1+b2+b3+…+b10=(2+1)+(22+2)+…+
=(2+22+…+210)+(1+2+…+10)
=+=2101.
19.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.
【考点】直线与平面垂直的性质;用空间向量求平面间的夹角.
【分析】(Ⅰ)因为∠DAB=60°,AB=2AD,由余弦定理得BD=,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;
(Ⅱ)建立空间直角坐标系,写出点A,B,C,P的坐标,求出向量,和平面PAB的法向量,平面PBC的法向量,求出这两个向量的夹角的余弦值即可.
【解答】(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=,
从而BD2+AD2=AB2,故BD⊥AD
又PD⊥底面ABCD,可得BD⊥PD
所以BD⊥平面PAD.故PA⊥BD
(Ⅱ)如图,以D为坐标原点,AD的长为单位长,
射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz,则
A(1,0,0),B(0,,0),C(﹣1,,0),P(0,0,1).
=(﹣1,,0),=(0,,﹣1),=(﹣1,0,0),
设平面PAB的法向量为=(x,y,z),则
即,
因此可取=(,1,)
设平面PBC的法向量为=(x,y,z),则,
即:
可取=(0,1,),cos<>==
故二面角A﹣PB﹣C的余弦值为:﹣.
20.椭圆=1(a>b>0)的离心率为,右焦点到直线x+y+=0的距离为2.
(Ⅰ)
求椭圆的方程;
(Ⅱ)
过点M(0,﹣1)作直线l交椭圆于A,B两点,交x轴于N点,满足=﹣,求直线l的方程.
【考点】直线与圆锥曲线的综合问题.
【分析】(Ⅰ)根据圆的离心率为,右焦点到直线x+y+=0的距离为2,建立方程组,可求椭圆的方程;
(Ⅱ)设A
(x1,y1),B(x2,y2),N(x0,0),利用=﹣,可得(x1﹣x0,y1)=﹣(x2﹣x0,y2),设直线l的方程为y=kx﹣1(k≠0),与椭圆方程联立,消去x可得(4k2+1)y2+2y+1﹣8k2=0,由此即可求得直线l的方程.
【解答】解:(Ⅰ)∵椭圆的离心率为,右焦点到直线x+y+=0的距离为2,
∴
∴c=,a=2,
∴b=,
∴椭圆的方程为;
(Ⅱ)设A
(x1,y1),B(x2,y2),N(x0,0)
∵=﹣,
∴(x1﹣x0,y1)=﹣(x2﹣x0,y2)
∴y1=﹣y2①
易知直线斜率不存在时或斜率为0时①不成立
于是设直线l的方程为y=kx﹣1(k≠0).
与椭圆方程联立,消去x可得(4k2+1)y2+2y+1﹣8k2=0②
∴y1+y2=﹣③y1y2=④
由①③可得y2=,y1=﹣代入④整理可得:8k4+k2﹣9=0
∴k2=1
此时②为5y2+2y﹣7=0,判别式大于0
∴直线l的方程为y=±x﹣1.
2016年10月8日
同课章节目录
