9.3一元一次不等式组的应用
图片预览





文档简介
课件20张PPT。
9.3一元一次不等式组的应用(2)本节学习目标:
1、进一步巩固一元一次不等式 组的解法。
2、会用一元一次不等式组解决有关的实际问题。
3、进一步巩固理解一元一次不等式组应用题的一般解题步骤,逐步形成分析问题和解决问题的能力。(1) 审题;
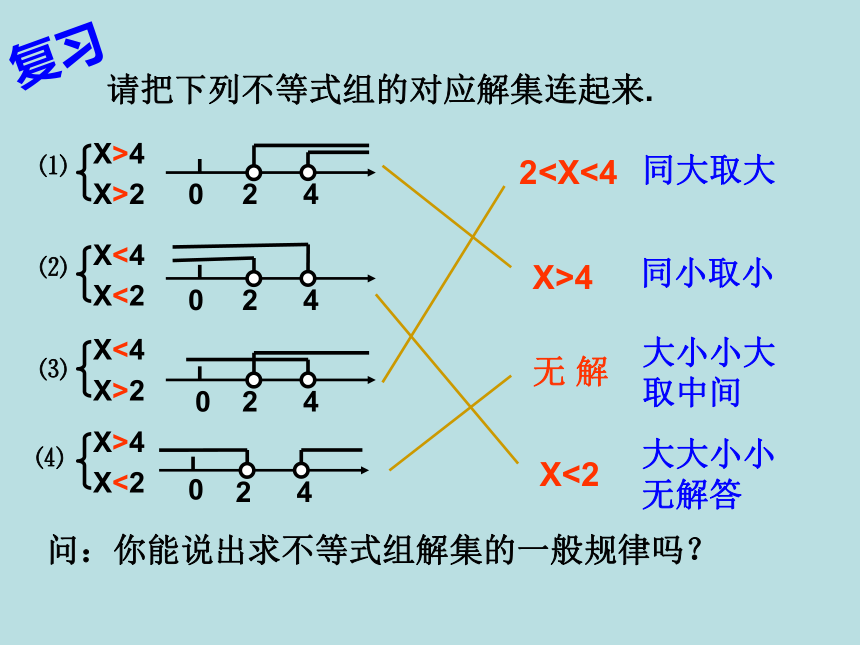
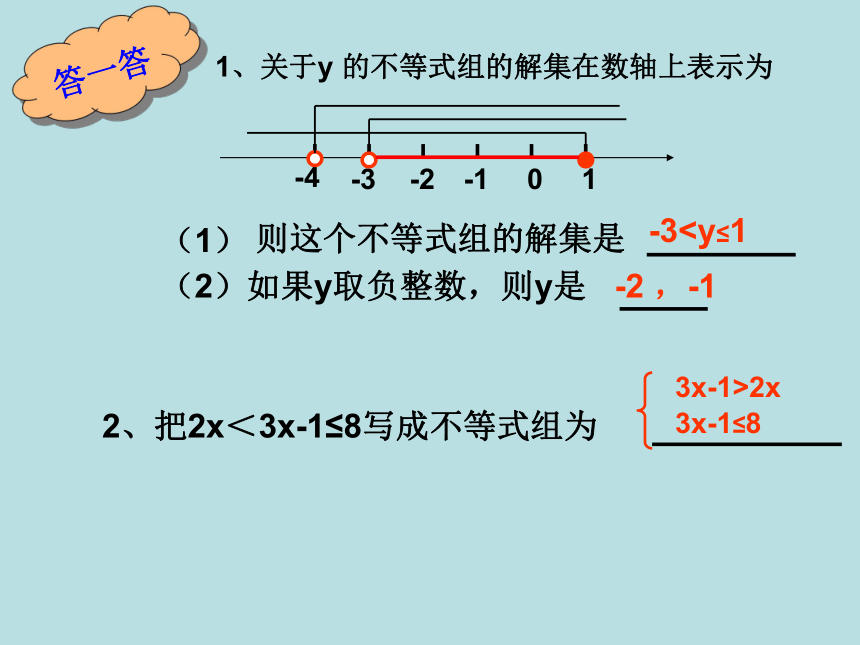
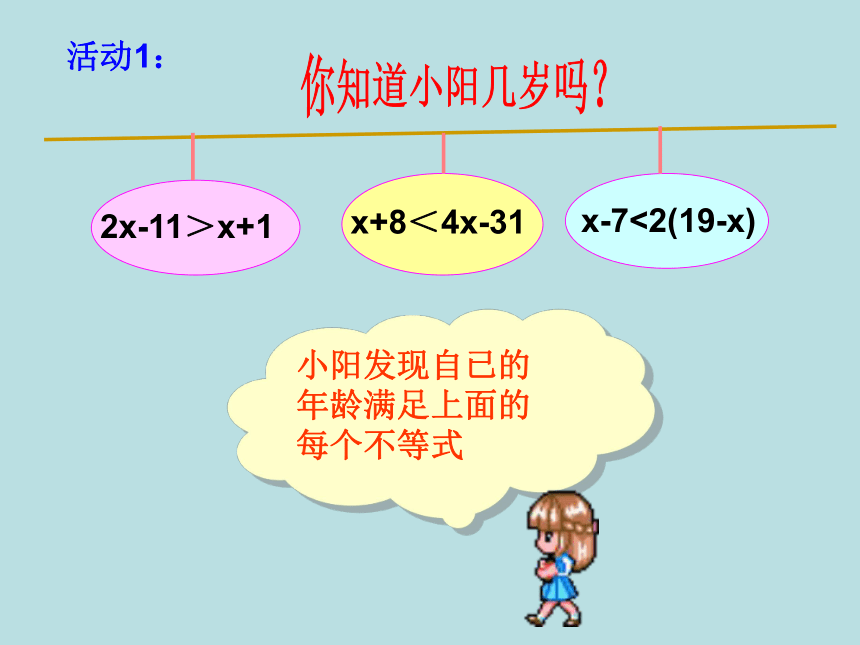
列一元一次不等式组解实际问题的 一般步骤:(2)找不等关系,设未知数;(3)根据不等关系列不等式组;(4)解不等式组;(5)由不等式组的解确立实际问题的解;(6)作答复习请把下列不等式组的对应解集连起来.024024024X>422x3x-1≤8(1)x+8<4x-31x-7<2(19-x)你知道小阳几岁吗?活动1:小阳发现自已的年龄满足上面的每个不等式
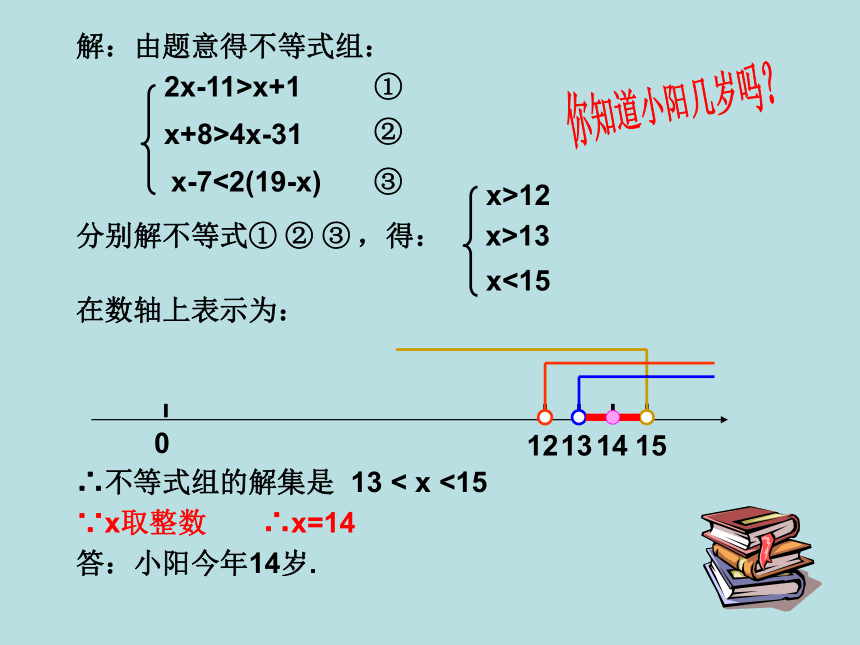
解:由题意得不等式组:2x-11>x+1x+8>4x-31x-7<2(19-x)③②①分别解不等式① ② ③ ,得:在数轴上表示为:120131415∴不等式组的解集是 13 < x <15x>12∵x取整数 ∴x=14答:小阳今年14岁.x<15x>13你知道小阳几岁吗?请问: 女儿的体重有多重? 3×女儿的体重﹤爸爸的体重 3×女儿的体重+小狗的体重﹥爸爸的体重
解:设女儿的体重为x千克,则:3x<723x+6>72 活动2:
女儿体重的3倍小于爸爸的体重,爸爸体重为72千克。女儿体重的三倍加上小狗的重量大于爸爸的体重.小狗的体重为6千克。解:设女儿的体重为x千克,
则3x<723x+6>72 ②①解不等式①,得:x<24解不等式②,得:x>22在数轴上表示为:∴不等式组的解集是 22实践应用,合作探索 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
生产A种产品所需的甲种原料+生产B种产品所需的甲种原料≤360
生产A种产品所需的乙种原料+生产B种产品所需的乙种原料≤290
根据上述关系可列不等式组:
9x+4(50-x)≤360
3x+10(50-x)≤290 解得:30≤x≤32(2) 可有三种生产方案:A种30件,B种20件或A种31件,B种19件或A种32件,B种18件
∵ x取正整数,思路分析:(1)本题的不等关系是:∴x=30、31、32
700×30+1200×20=45000元700×31+1200×19=44500元700×32+1200×18=44000元∵ 45000 > 44500 > 44000
∴应选择方案一, A种30件,B种20件,此时获利最大,最大利润是45000元。
(3)方案一:方案二:方案三:现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂有A、B两种不同规格的货车厢40节。如果每节A型车厢可装甲种货物35吨和乙种货物15吨;每节B型车厢可装甲种货物25吨和乙种货物35吨。装货时按此要求安排A、B两种车厢的节数有哪几种方案?
本题的不等关系是:A型车厢可装甲种货物+ B型车厢可装甲种货物≥ 1240
A型车厢可装乙种货物+ B型车厢可装乙种货物≥ 880
根据上述关系可列不等式组:35x+25(40-x) ≥ 1240
15x+35(40-x) ≥ 880解得:24≤x≤26
因为: x取正整数, x=24、25、26
(2) 可有三种生产方案:A种车厢24节,B种车厢16节或A种车厢25节B种车厢15节或A种车厢26节,B种车厢16节
归 纳: 对于具有多种不等关系的问题,可通过不等式组解决。
解一元一次不等式组时,一般先求出其中各个不等式的解集,再求出这些解集的公共部分。利用数轴可以直观地表示不等式组的解集,再结合实际问题求出符合实际问题的解。
你觉得列一元一次不等式组解应用题与列二元一次方程组解应用题的步骤一样吗?思考:一个未知数
两个未知数
找
不等关系
找
等量关系一个范围
一组数根据题意写出答案能力提升建筑公司急用普通水泥230吨,钢材168吨,现有A,B两种货车共40辆可使用.A种车可装普通水泥6吨和钢材4吨,运费1900元;B种车可装普通水泥5吨和钢材5吨,运费2000元.(1)要安排A,B两种车来运输,有几种方案?(2)哪种运输方案最省钱?为什么?
再见
9.3一元一次不等式组的应用(2)本节学习目标:
1、进一步巩固一元一次不等式 组的解法。
2、会用一元一次不等式组解决有关的实际问题。
3、进一步巩固理解一元一次不等式组应用题的一般解题步骤,逐步形成分析问题和解决问题的能力。(1) 审题;
列一元一次不等式组解实际问题的 一般步骤:(2)找不等关系,设未知数;(3)根据不等关系列不等式组;(4)解不等式组;(5)由不等式组的解确立实际问题的解;(6)作答复习请把下列不等式组的对应解集连起来.024024024X>42
解:由题意得不等式组:2x-11>x+1x+8>4x-31x-7<2(19-x)③②①分别解不等式① ② ③ ,得:在数轴上表示为:120131415∴不等式组的解集是 13 < x <15x>12∵x取整数 ∴x=14答:小阳今年14岁.x<15x>13你知道小阳几岁吗?请问: 女儿的体重有多重? 3×女儿的体重﹤爸爸的体重 3×女儿的体重+小狗的体重﹥爸爸的体重
解:设女儿的体重为x千克,则:3x<723x+6>72 活动2:
女儿体重的3倍小于爸爸的体重,爸爸体重为72千克。女儿体重的三倍加上小狗的重量大于爸爸的体重.小狗的体重为6千克。解:设女儿的体重为x千克,
则3x<723x+6>72 ②①解不等式①,得:x<24解不等式②,得:x>22在数轴上表示为:∴不等式组的解集是 22
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
生产A种产品所需的甲种原料+生产B种产品所需的甲种原料≤360
生产A种产品所需的乙种原料+生产B种产品所需的乙种原料≤290
根据上述关系可列不等式组:
9x+4(50-x)≤360
3x+10(50-x)≤290 解得:30≤x≤32(2) 可有三种生产方案:A种30件,B种20件或A种31件,B种19件或A种32件,B种18件
∵ x取正整数,思路分析:(1)本题的不等关系是:∴x=30、31、32
700×30+1200×20=45000元700×31+1200×19=44500元700×32+1200×18=44000元∵ 45000 > 44500 > 44000
∴应选择方案一, A种30件,B种20件,此时获利最大,最大利润是45000元。
(3)方案一:方案二:方案三:现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂有A、B两种不同规格的货车厢40节。如果每节A型车厢可装甲种货物35吨和乙种货物15吨;每节B型车厢可装甲种货物25吨和乙种货物35吨。装货时按此要求安排A、B两种车厢的节数有哪几种方案?
本题的不等关系是:A型车厢可装甲种货物+ B型车厢可装甲种货物≥ 1240
A型车厢可装乙种货物+ B型车厢可装乙种货物≥ 880
根据上述关系可列不等式组:35x+25(40-x) ≥ 1240
15x+35(40-x) ≥ 880解得:24≤x≤26
因为: x取正整数, x=24、25、26
(2) 可有三种生产方案:A种车厢24节,B种车厢16节或A种车厢25节B种车厢15节或A种车厢26节,B种车厢16节
归 纳: 对于具有多种不等关系的问题,可通过不等式组解决。
解一元一次不等式组时,一般先求出其中各个不等式的解集,再求出这些解集的公共部分。利用数轴可以直观地表示不等式组的解集,再结合实际问题求出符合实际问题的解。
你觉得列一元一次不等式组解应用题与列二元一次方程组解应用题的步骤一样吗?思考:一个未知数
两个未知数
找
不等关系
找
等量关系一个范围
一组数根据题意写出答案能力提升建筑公司急用普通水泥230吨,钢材168吨,现有A,B两种货车共40辆可使用.A种车可装普通水泥6吨和钢材4吨,运费1900元;B种车可装普通水泥5吨和钢材5吨,运费2000元.(1)要安排A,B两种车来运输,有几种方案?(2)哪种运输方案最省钱?为什么?
再见
