湖南省桃江县第四中学高中数学必修五课件:1.1 正余弦定理 (共18张PPT)
文档属性
| 名称 | 湖南省桃江县第四中学高中数学必修五课件:1.1 正余弦定理 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 378.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-08 00:00:00 | ||
图片预览





文档简介
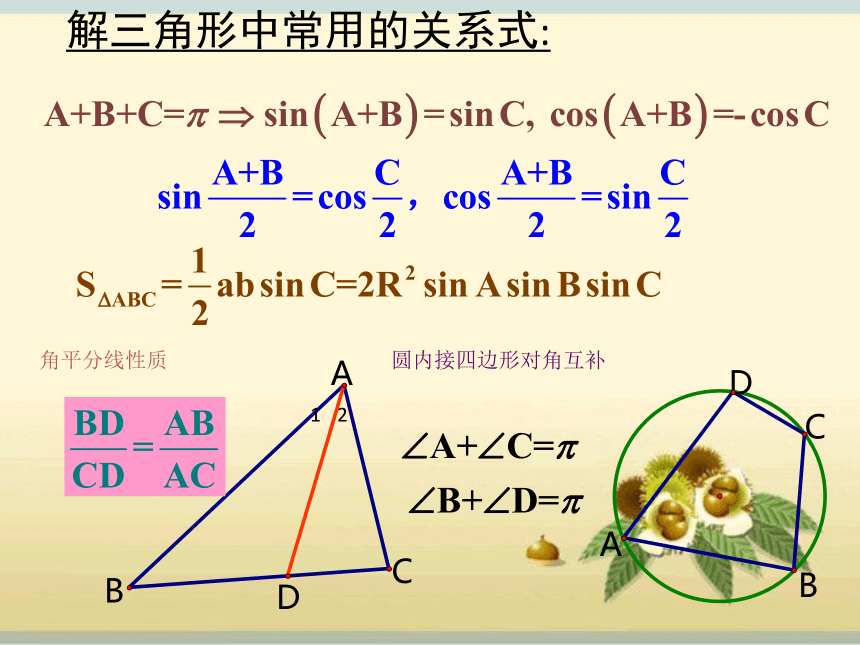
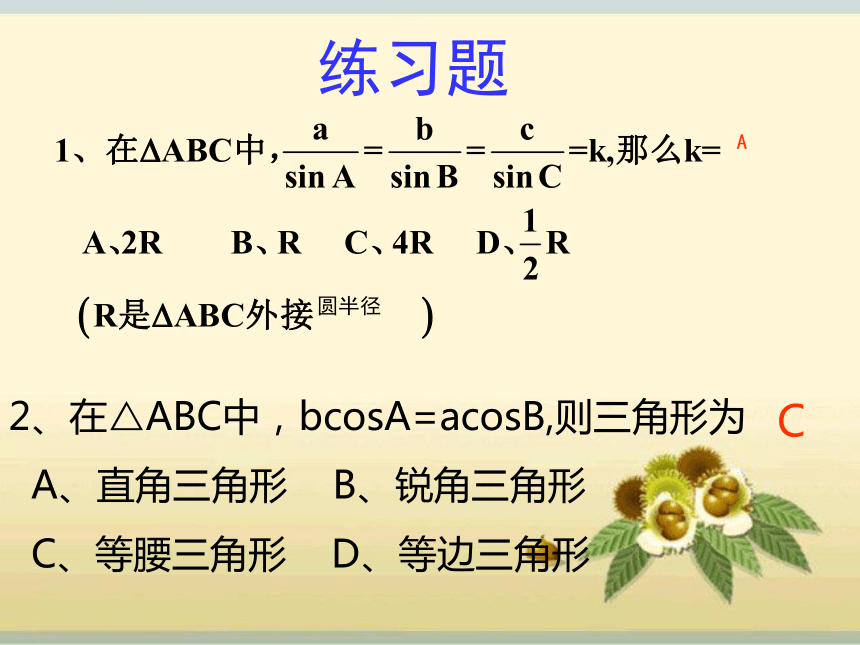
课件18张PPT。复习目标:1、进一步熟悉正余弦定理内容;2、能够应用正余弦定理进行边角关系的相互转化;3、能够利用正余弦定理判断三角形的形状;4、能够利用正余弦定理证明三角形中的三角恒等式。复习重点:利用正余弦定理进行边角互换难点:1、利用正余弦定理进行边角互换时的转化方向2、三角恒等式证明中结论与条件之间的内在联系的寻求。正、余弦定理复习回顾正弦定理:可以解决几类有关三角形的问题?(1)已知两角和任一边。 AAS(2)已知两边和一边的对角。SSA变形:(1)已知三边求三个角;(SSS)(2)已知两边和它们的夹角,求第三边和其他两个角. (SAS)余弦定理的作用(3)判断三角形的形状,求三角形的面积解三角形中常用的关系式:角平分线性质圆内接四边形对角互补由余弦定理易得:三角形面积计算公式练习题圆半径A2、在△ABC中,bcosA=acosB,则三角形为
A、直角三角形 B、锐角三角形
C、等腰三角形 D、等边三角形C3、在△ABC中,若a=6,b=7,c=8,则△ABC的形状是
A、锐角三角形 B、钝角三角形
C、直角三角形 D、无法确定A5、在△ABC中,cosAcosB>sinAsinB,则△ABC为
A、等边三角形 B、直角三角形
C、等腰三角形 D、等腰三角形或直角三角形C(事实上,C为钝角,只有C项适合)D6、在△ABC中,sin2A=sin2B+sinBsinC+sin2C,则A等于
A、30o B、60o C、120o D、150oA、等边三角形 B、直角三角形
C、等腰三角形 D、等腰三角形或直角三角形DC等腰三角形10、在△ABC中,A、B均为锐角,且cosA>sinB,则△ABC是_______________钝角三角形等腰三角形锐例2、已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积。解:连接BD(例1变式)(三维)边长和外接圆面积。(例1变式)试判断三角形的形状。三角形ABC是正三角形(三维)例6、根据所给条件,判断三角形ABC的形状。∴△ABC是等腰三角形或直角三角形tanA=tanB=tanC∴△ABC是等边三角形(例1变式)小结1、正弦定理和余弦定理的每一个等式中都包含三角形的四个元素,如果其中三个元素是已知的(其中至少有一边),那么这个三角形一定可解。2、正弦定理和余弦定理的特殊功能是边角互换,即利用它们可以把边的关系转化为角的关系,也可以把角的关系转化为边的关系,从而使许多问题得以解决。3、判断三角形的形状,一般考虑从两个方向进行变形。一个方向是边,走代数变形之路,通常正、余弦定理结合使用;另一个方向是角,走三角变形之路,通常是运用正弦定理,要注意边角转化的桥梁----正、余弦定理。4、根据条件选用定理可使解题简便1)已知两角及其中一个角的对边,选用正弦定理,如已知A,B,a解三角形,则用正弦定理。2)已知三边a,b,c,一般选用余弦定理求角3)已知两边和它们的夹角,用余弦定理求第三边再用正弦定理求角。4)已知两边和一边的对角,用正弦定理求一个角,但需要进行讨论,有两解的可能。
A、直角三角形 B、锐角三角形
C、等腰三角形 D、等边三角形C3、在△ABC中,若a=6,b=7,c=8,则△ABC的形状是
A、锐角三角形 B、钝角三角形
C、直角三角形 D、无法确定A5、在△ABC中,cosAcosB>sinAsinB,则△ABC为
A、等边三角形 B、直角三角形
C、等腰三角形 D、等腰三角形或直角三角形C(事实上,C为钝角,只有C项适合)D6、在△ABC中,sin2A=sin2B+sinBsinC+sin2C,则A等于
A、30o B、60o C、120o D、150oA、等边三角形 B、直角三角形
C、等腰三角形 D、等腰三角形或直角三角形DC等腰三角形10、在△ABC中,A、B均为锐角,且cosA>sinB,则△ABC是_______________钝角三角形等腰三角形锐例2、已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积。解:连接BD(例1变式)(三维)边长和外接圆面积。(例1变式)试判断三角形的形状。三角形ABC是正三角形(三维)例6、根据所给条件,判断三角形ABC的形状。∴△ABC是等腰三角形或直角三角形tanA=tanB=tanC∴△ABC是等边三角形(例1变式)小结1、正弦定理和余弦定理的每一个等式中都包含三角形的四个元素,如果其中三个元素是已知的(其中至少有一边),那么这个三角形一定可解。2、正弦定理和余弦定理的特殊功能是边角互换,即利用它们可以把边的关系转化为角的关系,也可以把角的关系转化为边的关系,从而使许多问题得以解决。3、判断三角形的形状,一般考虑从两个方向进行变形。一个方向是边,走代数变形之路,通常正、余弦定理结合使用;另一个方向是角,走三角变形之路,通常是运用正弦定理,要注意边角转化的桥梁----正、余弦定理。4、根据条件选用定理可使解题简便1)已知两角及其中一个角的对边,选用正弦定理,如已知A,B,a解三角形,则用正弦定理。2)已知三边a,b,c,一般选用余弦定理求角3)已知两边和它们的夹角,用余弦定理求第三边再用正弦定理求角。4)已知两边和一边的对角,用正弦定理求一个角,但需要进行讨论,有两解的可能。
