湖南省桃江县第四中学高中数学必修五课件:2.1 数列的概念与简单表示法 (共28张PPT)
文档属性
| 名称 | 湖南省桃江县第四中学高中数学必修五课件:2.1 数列的概念与简单表示法 (共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 727.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-08 16:40:22 | ||
图片预览







文档简介
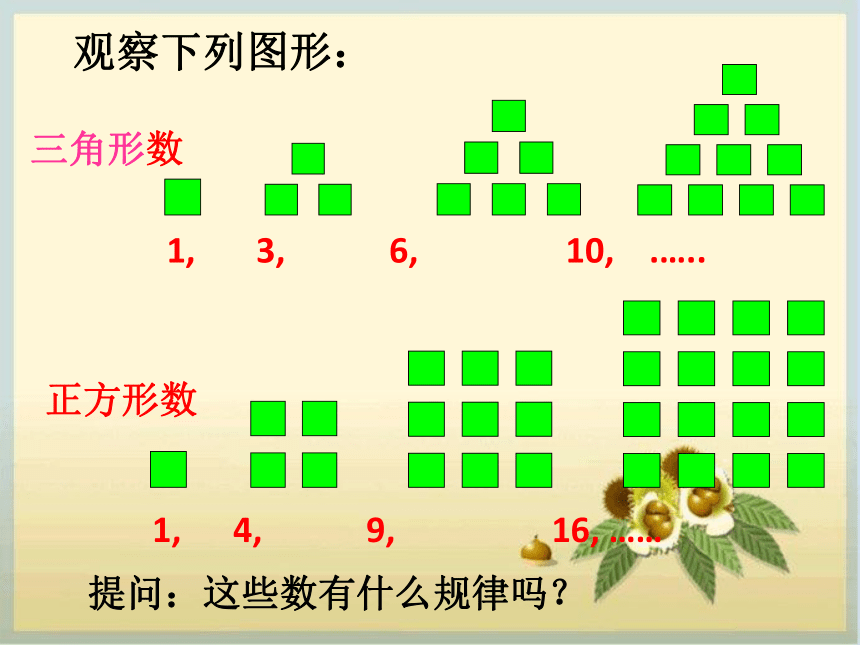
课件28张PPT。2.1数列的概念与简单表示法456781567812334264个格子1223344551667788OK456781456781233264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的2倍且共有64格子麦粒总数???1844,6744,0737,0955,1615三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……观察下列图形:提问:这些数有什么规律吗?一.定义: 按照一定顺序排列着的一列数叫数列。(1)三角形数:1, 3, 6, 10, .….. (2)正方形数:1, 4, 9, 16, ……数列中的每一个数叫做这个数列的项。 (3)4,5,6,7,8,9,10;
(4)10,9,8,7,6,5,4; 数列中的每一项都和它的序号有关,排第一位的数称为这个数列的第1项(通常叫做首项), 排第二位的数称为这个数列的第2项,······,
排第 n 位的数称为这个数列的第n项.
数列的一般形式可以写成: (1)三角形数:1, 3, 6, 10, .….. (2)正方形数:1, 4, 9, 16, …… 按照一定顺序排列着的一列数叫数列。(1)三角形数:1, 3, 6, 10, .….. (2)正方形数:1, 4, 9, 16, ……一.定义: 按照一定顺序排列的一列数叫数列。思考1:数列 4,5,6,7,8,9,10;
数列 10,9,8,7,6,5,4;是否相同?思考2:数列中的数是否可以重复?
如:数列-1,1,-1,1,···。
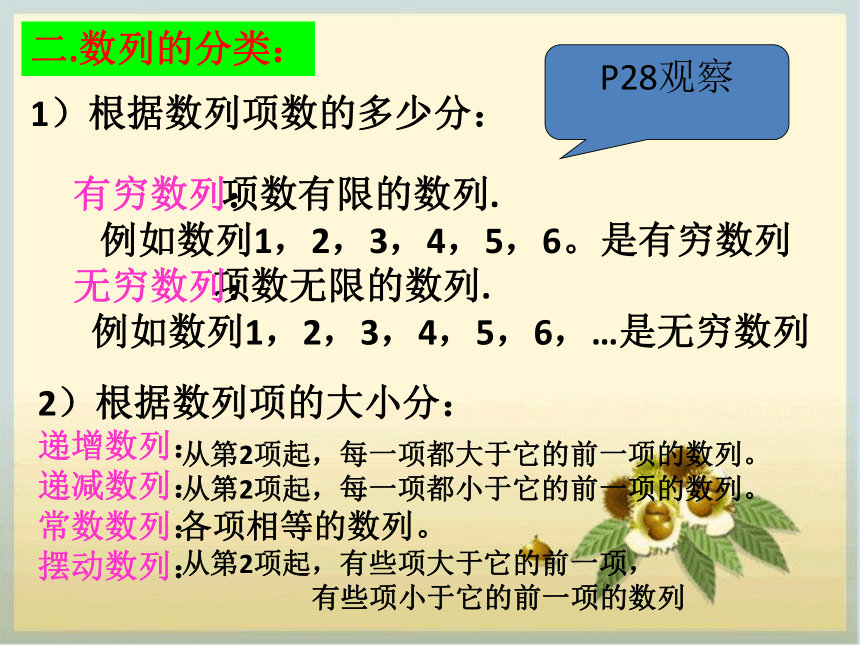
项数有限的数列.
例如数列1,2,3,4,5,6。是有穷数列
项数无限的数列.
例如数列1,2,3,4,5,6,…是无穷数列1)根据数列项数的多少分:二.数列的分类: P28观察有穷数列:
无穷数列:2)根据数列项的大小分:
递增数列:
递减数列:
常数数列:
摆动数列:
从第2项起,每一项都大于它的前一项的数列。
从第2项起,每一项都小于它的前一项的数列。
各项相等的数列。
从第2项起,有些项大于它的前一项,
有些项小于它的前一项的数列⑴全体自然数构成数列:
⑵1996~2002年某市普通高中生人数(单位:万人)0,1,2,3, … .
82,93,105,119,129,130,132.构成数列
⑶无穷多个3构成数列3,3,3,3,3, … .⑷目前通用的人民币面额从大到小的顺序构成数列(单位:元)100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01.⑸-1的1次幂, 2次幂, 3次幂, 4次幂 构成数列-1,1,-1,1, … .……递增数列递减数列常数列递增数列摆动数列以下数列属于哪种分类? 观察下列数列的每一项与这一项的序号是否有一定的对应关系? 1 2 3 4 5 ….项序号2, 4, 6, 8, 10,…1 2 3 4 5 ……序号项 数列中的每一个数都对应着一个序号,反过来,每个序号也都对应着一个数。三.数列的表示: nn2n数列与函数的关系 : 数列可以看作特殊的函数,序号是其自变量,项是序号所对应的函数值,数列的定义域是正整数集 ,或是正整数集 的有限子集 . 于是我们研究数列就可借用函数的研究方法,用函数的观点看待数列. 数列可以看成以正整数集N*(或它的有限子集{1,2,3,4,…,n})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值。思考正方形数:1, 4, 9, 16, …… 通项公式可以看成是数列的函数解析式。 如果只知道数列的通项公式,那能写出这个数列吗?例1、 写出下面数列的一个通项公式,使它的 前4项分别是下列各数: 练习:P31 1,3,4数列 2,4,6,8,10,……
其通项公式是:图象为:an
10
9
8
7
6
5
4
3
2 0 1 2 3 4 5 n例2、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n问题:如果一个数列{an}的首项a1=1,从第二项起每一项等于它的前一项的2倍再加1,
即 an = 2 an-1 + 1(n∈N,n>1),(※)你能写出这个数列的前三项吗?递推公式例3 设数列 满足 写出这个数列的前五项。练习:P31 2例3 设数列 满足 递推公式是数列所特有的表示法,它包含两个部分:递推关系和初始条件,二者缺一不可. 观察下面数列的特点,用适当的数
填空,并写出每个数列的一个通项公式: 练 习 题写出下面数列的一个通项公式,
使它的前4项分别是下列各数: 练 习 题练习:根据下面数列的前几项的值,写出数列的一个通项公式:讲解范例:例2. 已知数列{an}的通项公式为
an=log2(n2+3)-2,
求log23是这个数列的第几项?例1. 求数列{-2n2+9n+3}中的最大项.1.由数字1,2,3,4四个数字一共可以组成多少个不同的数列?2. 已知数列{an}的通项公式为 ,试判断 和 是不是它的项?如果是,是第几项? 练 习 题补充练习小结1、数列的定义
2、数列的实质—特殊的函数(离散函数)
3、数列的通项公式
4、数列的表示方法:
列表法,
通项公式法,
图象法,
递推公式法
(4)10,9,8,7,6,5,4; 数列中的每一项都和它的序号有关,排第一位的数称为这个数列的第1项(通常叫做首项), 排第二位的数称为这个数列的第2项,······,
排第 n 位的数称为这个数列的第n项.
数列的一般形式可以写成: (1)三角形数:1, 3, 6, 10, .….. (2)正方形数:1, 4, 9, 16, …… 按照一定顺序排列着的一列数叫数列。(1)三角形数:1, 3, 6, 10, .….. (2)正方形数:1, 4, 9, 16, ……一.定义: 按照一定顺序排列的一列数叫数列。思考1:数列 4,5,6,7,8,9,10;
数列 10,9,8,7,6,5,4;是否相同?思考2:数列中的数是否可以重复?
如:数列-1,1,-1,1,···。
项数有限的数列.
例如数列1,2,3,4,5,6。是有穷数列
项数无限的数列.
例如数列1,2,3,4,5,6,…是无穷数列1)根据数列项数的多少分:二.数列的分类: P28观察有穷数列:
无穷数列:2)根据数列项的大小分:
递增数列:
递减数列:
常数数列:
摆动数列:
从第2项起,每一项都大于它的前一项的数列。
从第2项起,每一项都小于它的前一项的数列。
各项相等的数列。
从第2项起,有些项大于它的前一项,
有些项小于它的前一项的数列⑴全体自然数构成数列:
⑵1996~2002年某市普通高中生人数(单位:万人)0,1,2,3, … .
82,93,105,119,129,130,132.构成数列
⑶无穷多个3构成数列3,3,3,3,3, … .⑷目前通用的人民币面额从大到小的顺序构成数列(单位:元)100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01.⑸-1的1次幂, 2次幂, 3次幂, 4次幂 构成数列-1,1,-1,1, … .……递增数列递减数列常数列递增数列摆动数列以下数列属于哪种分类? 观察下列数列的每一项与这一项的序号是否有一定的对应关系? 1 2 3 4 5 ….项序号2, 4, 6, 8, 10,…1 2 3 4 5 ……序号项 数列中的每一个数都对应着一个序号,反过来,每个序号也都对应着一个数。三.数列的表示: nn2n数列与函数的关系 : 数列可以看作特殊的函数,序号是其自变量,项是序号所对应的函数值,数列的定义域是正整数集 ,或是正整数集 的有限子集 . 于是我们研究数列就可借用函数的研究方法,用函数的观点看待数列. 数列可以看成以正整数集N*(或它的有限子集{1,2,3,4,…,n})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值。思考正方形数:1, 4, 9, 16, …… 通项公式可以看成是数列的函数解析式。 如果只知道数列的通项公式,那能写出这个数列吗?例1、 写出下面数列的一个通项公式,使它的 前4项分别是下列各数: 练习:P31 1,3,4数列 2,4,6,8,10,……
其通项公式是:图象为:an
10
9
8
7
6
5
4
3
2 0 1 2 3 4 5 n例2、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n问题:如果一个数列{an}的首项a1=1,从第二项起每一项等于它的前一项的2倍再加1,
即 an = 2 an-1 + 1(n∈N,n>1),(※)你能写出这个数列的前三项吗?递推公式例3 设数列 满足 写出这个数列的前五项。练习:P31 2例3 设数列 满足 递推公式是数列所特有的表示法,它包含两个部分:递推关系和初始条件,二者缺一不可. 观察下面数列的特点,用适当的数
填空,并写出每个数列的一个通项公式: 练 习 题写出下面数列的一个通项公式,
使它的前4项分别是下列各数: 练 习 题练习:根据下面数列的前几项的值,写出数列的一个通项公式:讲解范例:例2. 已知数列{an}的通项公式为
an=log2(n2+3)-2,
求log23是这个数列的第几项?例1. 求数列{-2n2+9n+3}中的最大项.1.由数字1,2,3,4四个数字一共可以组成多少个不同的数列?2. 已知数列{an}的通项公式为 ,试判断 和 是不是它的项?如果是,是第几项? 练 习 题补充练习小结1、数列的定义
2、数列的实质—特殊的函数(离散函数)
3、数列的通项公式
4、数列的表示方法:
列表法,
通项公式法,
图象法,
递推公式法
