湖南省桃江县第四中学高中数学必修五课件:3.3.1 二元一次不等式(组)与平面区域 (共20张PPT)
文档属性
| 名称 | 湖南省桃江县第四中学高中数学必修五课件:3.3.1 二元一次不等式(组)与平面区域 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-08 16:54:35 | ||
图片预览







文档简介
课件20张PPT。二元一次不等式(组)
与平面区域实例引入: 问题2:已知6枝玫瑰与3枝康乃馨的价格之和
大于24元,而4枝玫瑰与5枝康乃馨的价格之和
小于22元,求玫瑰和康乃馨的价格。 问题1 :已知两实数的和小于20,求两实数。x+y<20二元一次不等式二元一次不等式组思考?我们知道一元一次不等式x>3的解集可以
表示为数轴上的区间,那么,在直角坐标
系内,二元一次不等式(组)的解集表示
什么图形?比如,解不等式x-y<1.
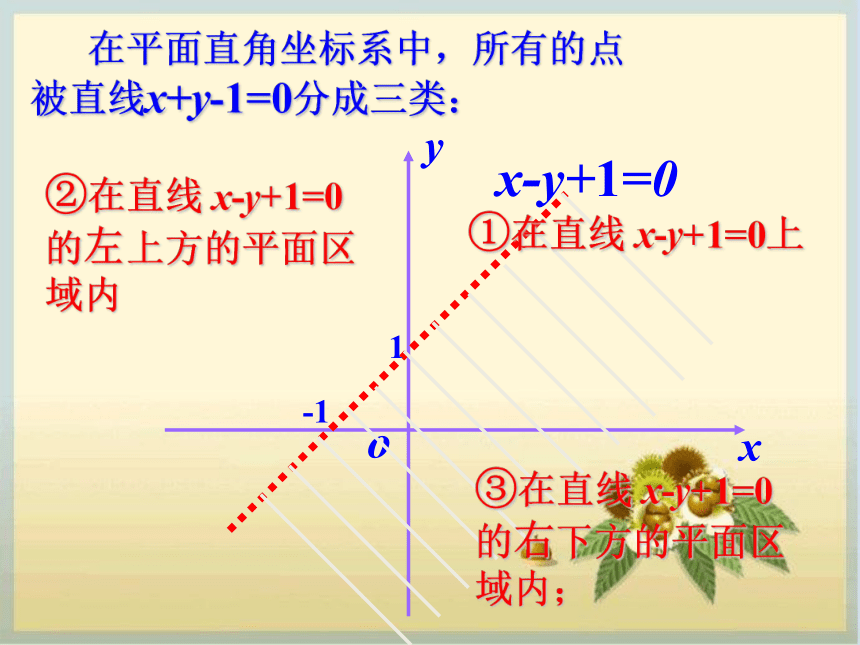
或者不等式组X+y>3X-y<81-1x-y+1=0 在平面直角坐标系中,所有的点
被直线x+y-1=0分成三类:①在直线 x-y+1=0上③在直线 x-y+1=0 的右下方的平面区域内;②在直线 x-y+1=0 的左上方的平面区域内xx+1-y=0在直线 x-y+1=0 的左上方的平面区域内的点的特点:把点的坐标代入式子
x+1-y,
判断式子的符号。坐标符合不等式x-y+1构成的区域
或者说
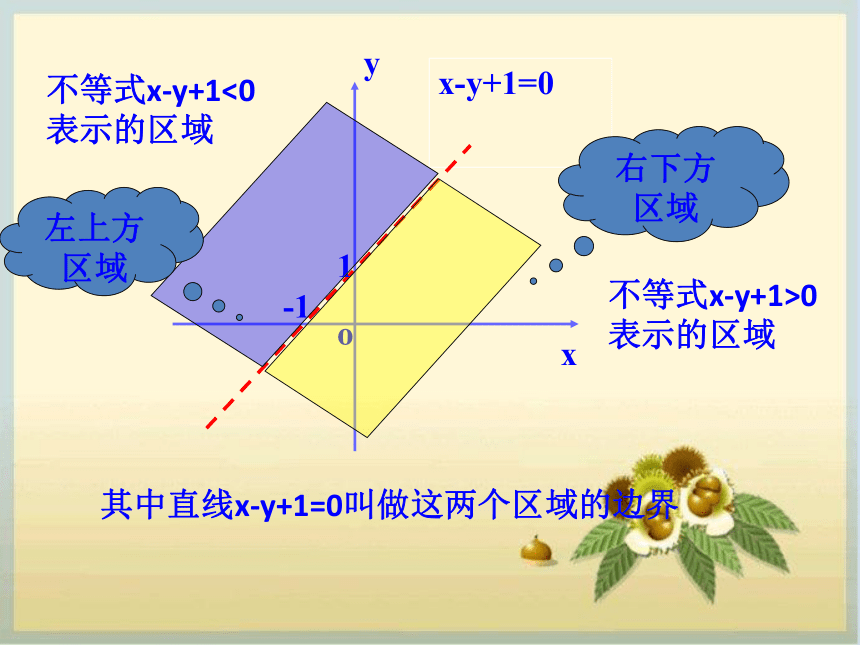
不等式x-y+1<0表示的区域左上方区域yxo1-1不等式x-y+1>0
表示的区域右下方区域其中直线x-y+1=0叫做这两个区域的边界不等式x-y+1<0
表示的区域左上方区域xy0右上方区域左下方区域二元一次不等式Ax+By+C>0在平面直角坐标系中表示: 直线Ax+By+C=0某一侧所有点组成的平面区域。我们把直线画成虚线表示区域不包括边界。
不等式Ax+By+C≥0表示的平面区域包括边界,把边界画成实线。我们得到:二元一次不等式表示哪个平面区域的判断方法: 直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同。结论:直线定界,特殊点定域。 只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域。特别的:C≠0时,常把原点作为特殊点;
C=0时,常把(1,0),(0,1)作为特点; 例题示范:例1:画出不等式 x + 4y < 4表示的平面区域 解:(1)(直线定界):先画直线x + 4y – 4 = 0(画成虚线)(2)(特殊点定域):取原点(0,0),代入x + 4y - 4,因为 0 + 4×0 – 4 = -4 < 0所以,原点在x + 4y – 4 < 0表示的平面区域内,
不等式x + 4y – 4 < 0表示的区域如图所示。1、不等式x-2y+6>0表示的区域在直线x-2y+6=0的( )A、右上方B、右下方C、左上方D、左下方2、不等式3x+2y-6≤0表示的平面区域是( )ABC跟踪练习1:BC跟踪练习2、 将下列图中的平面区域(阴影部分)用不等式出来(图(1)中的区域不包含y轴)解(1) x>0(2) x+y≥0(3) 2x+y<4y < -3x+12
x<2y 的解集。例2、用平面区域表示不等式组分析:由于所求平面区域的点的坐标要同时满足两个不等式,一次二元一次不等式组表示的平面区域是各个不等式表示的平面区域的交集,即各个不等式表示的平面区域的公共部分。课堂练习:3、不等式组B表示的平面区域是( )例4、已知点 和 在直线 的两侧,
则 的取值范围是
解:依题意必有即练习:2、画出下列不等式组表示的平面区域:应该注意的几个问题:1、若不等式中不含0,则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。否则应画成实线。 数学思想:数形结合4、 小结 知识点: ⑴ 二元一次不等式表示平面区域
直线某一侧所有点组成的平面区域 ⑵ 判定方法:
直线定界,特殊点定域。 数学思想:数形结合
大于24元,而4枝玫瑰与5枝康乃馨的价格之和
小于22元,求玫瑰和康乃馨的价格。 问题1 :已知两实数的和小于20,求两实数。x+y<20二元一次不等式二元一次不等式组思考?我们知道一元一次不等式x>3的解集可以
表示为数轴上的区间,那么,在直角坐标
系内,二元一次不等式(组)的解集表示
什么图形?比如,解不等式x-y<1.
或者不等式组X+y>3X-y<81-1x-y+1=0 在平面直角坐标系中,所有的点
被直线x+y-1=0分成三类:①在直线 x-y+1=0上③在直线 x-y+1=0 的右下方的平面区域内;②在直线 x-y+1=0 的左上方的平面区域内xx+1-y=0在直线 x-y+1=0 的左上方的平面区域内的点的特点:把点的坐标代入式子
x+1-y,
判断式子的符号。坐标符合不等式x-y+1
或者说
不等式x-y+1<0表示的区域左上方区域yxo1-1不等式x-y+1>0
表示的区域右下方区域其中直线x-y+1=0叫做这两个区域的边界不等式x-y+1<0
表示的区域左上方区域xy0右上方区域左下方区域二元一次不等式Ax+By+C>0在平面直角坐标系中表示: 直线Ax+By+C=0某一侧所有点组成的平面区域。我们把直线画成虚线表示区域不包括边界。
不等式Ax+By+C≥0表示的平面区域包括边界,把边界画成实线。我们得到:二元一次不等式表示哪个平面区域的判断方法: 直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同。结论:直线定界,特殊点定域。 只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域。特别的:C≠0时,常把原点作为特殊点;
C=0时,常把(1,0),(0,1)作为特点; 例题示范:例1:画出不等式 x + 4y < 4表示的平面区域 解:(1)(直线定界):先画直线x + 4y – 4 = 0(画成虚线)(2)(特殊点定域):取原点(0,0),代入x + 4y - 4,因为 0 + 4×0 – 4 = -4 < 0所以,原点在x + 4y – 4 < 0表示的平面区域内,
不等式x + 4y – 4 < 0表示的区域如图所示。1、不等式x-2y+6>0表示的区域在直线x-2y+6=0的( )A、右上方B、右下方C、左上方D、左下方2、不等式3x+2y-6≤0表示的平面区域是( )ABC跟踪练习1:BC跟踪练习2、 将下列图中的平面区域(阴影部分)用不等式出来(图(1)中的区域不包含y轴)解(1) x>0(2) x+y≥0(3) 2x+y<4y < -3x+12
x<2y 的解集。例2、用平面区域表示不等式组分析:由于所求平面区域的点的坐标要同时满足两个不等式,一次二元一次不等式组表示的平面区域是各个不等式表示的平面区域的交集,即各个不等式表示的平面区域的公共部分。课堂练习:3、不等式组B表示的平面区域是( )例4、已知点 和 在直线 的两侧,
则 的取值范围是
解:依题意必有即练习:2、画出下列不等式组表示的平面区域:应该注意的几个问题:1、若不等式中不含0,则边界应画成虚线,2、画图时应非常准确,否则将得不到正确结果。3、熟记“直线定界、特殊点定域”方法的内涵。否则应画成实线。 数学思想:数形结合4、 小结 知识点: ⑴ 二元一次不等式表示平面区域
直线某一侧所有点组成的平面区域 ⑵ 判定方法:
直线定界,特殊点定域。 数学思想:数形结合
