湖南省桃江县第四中学高中数学必修五课件:第一章 解三角形 (共35张PPT)
文档属性
| 名称 | 湖南省桃江县第四中学高中数学必修五课件:第一章 解三角形 (共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 483.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-08 16:56:41 | ||
图片预览











文档简介
课件35张PPT。1.2 应用举例高一数学必修五第一章
解三角形第一课时 3、正弦定理的变形:2、三角形面积公式:复习回顾推论余弦定理:几个概念:仰角:目标视线在水平线上方的叫仰角;
俯角:目标视线在水平线下方的叫俯角;
方位角:北方向线顺时针方向到目标方向线的夹角。N方位角60度水平线目标方向线视线视线仰角俯角“遥不可及的月亮离我们地球究竟有多远呢?” 在古代,天文学家没有先进的仪器就已经估算出了两者的距离,是什么神奇的方法探索到这个奥秘的呢?我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形等等不同的方法,但由于在实际测量问题的真实背景下,某些方法会不能实施。如因为没有足够的空间,不能用全等三角形的方法来测量,所以,有些方法会有局限性。于是上面介绍的问题是用以前的方法所不能解决的。今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用,首先研究如何测量距离。创设情境 解决实际测量问题的过程一般要充
分认真理解题意,正确做出图形,把实
际问题里的条件和所求转换成三角形中
的已知和未知的边、角,通过建立数学
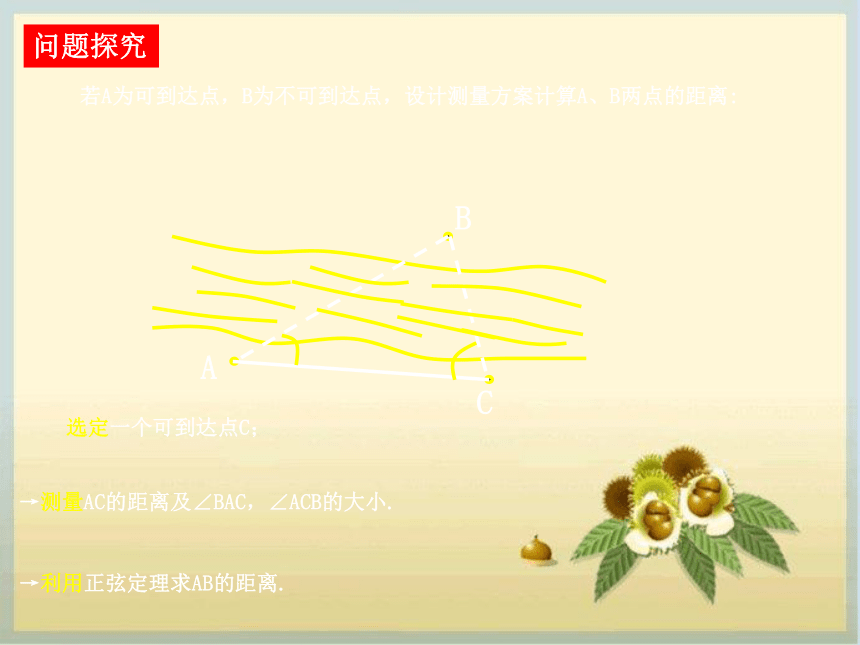
模型来求解。创设情境1.如图,设A、B两点在河的两岸,测量者在点A的同侧,如何求出A、B两点的距离?问题探究CAB在点A所在河岸边选定一点C,若测出A、C的距离是55m,∠BAC=51°,∠ACB=75°,求AB的长.CAB例1.设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同侧,在其所在的河岸边选定一点C,测出AC的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)51o75o55m解:如图,在△ABC中,B=180o-(51o+75o)=54o所以由可得答:A、B两点间的距离约为65.7米。ABC若A为可到达点,B为不可到达点,设计测量方案计算A、B两点的距离:选定一个可到达点C; →测量AC的距离及∠BAC,∠ACB的大小. →利用正弦定理求AB的距离.问题探究2.设A、B两点都在河的对岸(不可到达),你能设计一个测量方案计算A、B两点间的距离吗?D问题探究二、应用举例AB解:如图,测量者可以在河岸边选定两点C、D,设CD=a,∠BCA=α,∠ACD=β,∠CDB=γ,
∠ADB=δa例2.A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。ABCD为了测定河对岸两点A、B间的距离,在岸边选定1公里长的基线CD,并测得∠ACD=90o, ∠BCD=60o,∠BDC=75o,∠ADC=30o,求A、B两点的距离.练习问题解决选定两个可到达点C、D; →测量C、D间的距离及∠ACB、∠ACD、∠BDC、∠ADB的大小;→利用正弦定理求AC和BC; →利用余弦定理求AB.测量两个不可到达点之间的距离方案:形成规律在测量上,根据测量需要适当确定的线段叫做基线,如例1中的AC,例2中的CD.基线的选取不唯一,一般基线越长,测量的精确度越高.形成结论解斜三角形应用题的一般步骤:(1)分析:理解题意,分清已知与未知,
画出示意图(2)建模:根据已知条件与求解目标,把
已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型(3)求解:利用正弦定理或余弦定理有序地
解出三角形,求得数学模型的解(4)检验:检验上述所求的解是否符合实际
意义,从而得出实际问题的解 练习1.一艘船以32.2n mile / h的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向,30min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 已知△ABC中AB=1.95m,AC=1.40m,夹角∠CAB=66°20′,求BC.解:由余弦定理,得答:顶杆BC约长1.89m。 例3 .设AB是一个底部不可到达的竖直建筑物,A为建筑物的最高点,如何测量和计算建筑物AB的高度.CABEHG设在点C、D处测得A的仰角分别为α、β,CD=a,测角仪器的高度为h,试求建筑物高度AB.CABEHG问题探究D如图,在山顶上有一座铁塔BC,塔顶和塔底都可到达,A为地面上一点,通过测量哪些数据,可以计算出山顶的高度?设在点A处测得点B、C的仰角分别为α、β,铁塔的高BC=a,测角仪的高度忽略不计,试求山顶高度CD .问题解决例4.在山顶铁塔上B处测得地面上
一点A的俯角a =54°40′,在塔
底C处测得A处的俯角b =50°1′。
已知铁塔BC部分的高为27.3m,
求出山高CD(精确到1m)解:依题意可知,在△ABC中,
∠ABC=90o-a, ∠BAD=a , ∠CAD=b
∴∠BAC=a-b
∵根据正弦定理,1047m问题探究1.在测量上,根据测量需要适当确定的线段叫做基线.课堂小结2.距离测量问题包括一个不可到达点和两个不可到达点两种,设计测量方案的基本原则是:能够根据测量所得的数据计算所求两点间的距离,其中测量数据与基线的选取有关,计算时需要利用正、余弦定理.课堂小结3.解决物体高度测量问题时,一般先从一个或两个可到达点,测量出物体顶部或底部的仰角、俯角或方位角,再解三角形求相关数据.具体测量哪个类型的角,应根据实际情况而定.通常在地面测仰角,在空中测俯角,在行进中测方位角.课堂小结4.计算物体的高度时,一般先根据测量数据,利用正弦定理或余弦定理计算出物体顶部或底部到一个可到达点的距离,再解直角三角形求高度.150m补充练习 2 如图,有大小两座塔AB和CD,小塔的高为h,在小塔的底部A和顶部B测得另一塔顶D的仰角分别为α、β,求塔CD的高度.3 .飞机的海拔飞行高度是可知的,若飞机的航线和山顶在同一个铅垂平面内,飞机在水平飞行中测量山顶的高度,关键是求出哪个数据?飞机与山顶的海拔差 问题探究如图,设飞机在飞临山顶前,在B、C两处测得山顶A的俯角分别是α、β,B、C两点的飞行距离为a,飞机的海拔飞行高度是H,试求山顶的海拔高度h .作业:学海第4课时例题讲解 练1 在△ABC中,内角A,B,C对边的
边长分别是a,b,c.已知 (1)若△ABC的面积等于 ,求a,b. (2)sinC+sin(B-A)=2sin2A,求△ABC的面积.作业
解三角形第一课时 3、正弦定理的变形:2、三角形面积公式:复习回顾推论余弦定理:几个概念:仰角:目标视线在水平线上方的叫仰角;
俯角:目标视线在水平线下方的叫俯角;
方位角:北方向线顺时针方向到目标方向线的夹角。N方位角60度水平线目标方向线视线视线仰角俯角“遥不可及的月亮离我们地球究竟有多远呢?” 在古代,天文学家没有先进的仪器就已经估算出了两者的距离,是什么神奇的方法探索到这个奥秘的呢?我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形等等不同的方法,但由于在实际测量问题的真实背景下,某些方法会不能实施。如因为没有足够的空间,不能用全等三角形的方法来测量,所以,有些方法会有局限性。于是上面介绍的问题是用以前的方法所不能解决的。今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用,首先研究如何测量距离。创设情境 解决实际测量问题的过程一般要充
分认真理解题意,正确做出图形,把实
际问题里的条件和所求转换成三角形中
的已知和未知的边、角,通过建立数学
模型来求解。创设情境1.如图,设A、B两点在河的两岸,测量者在点A的同侧,如何求出A、B两点的距离?问题探究CAB在点A所在河岸边选定一点C,若测出A、C的距离是55m,∠BAC=51°,∠ACB=75°,求AB的长.CAB例1.设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同侧,在其所在的河岸边选定一点C,测出AC的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)51o75o55m解:如图,在△ABC中,B=180o-(51o+75o)=54o所以由可得答:A、B两点间的距离约为65.7米。ABC若A为可到达点,B为不可到达点,设计测量方案计算A、B两点的距离:选定一个可到达点C; →测量AC的距离及∠BAC,∠ACB的大小. →利用正弦定理求AB的距离.问题探究2.设A、B两点都在河的对岸(不可到达),你能设计一个测量方案计算A、B两点间的距离吗?D问题探究二、应用举例AB解:如图,测量者可以在河岸边选定两点C、D,设CD=a,∠BCA=α,∠ACD=β,∠CDB=γ,
∠ADB=δa例2.A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。ABCD为了测定河对岸两点A、B间的距离,在岸边选定1公里长的基线CD,并测得∠ACD=90o, ∠BCD=60o,∠BDC=75o,∠ADC=30o,求A、B两点的距离.练习问题解决选定两个可到达点C、D; →测量C、D间的距离及∠ACB、∠ACD、∠BDC、∠ADB的大小;→利用正弦定理求AC和BC; →利用余弦定理求AB.测量两个不可到达点之间的距离方案:形成规律在测量上,根据测量需要适当确定的线段叫做基线,如例1中的AC,例2中的CD.基线的选取不唯一,一般基线越长,测量的精确度越高.形成结论解斜三角形应用题的一般步骤:(1)分析:理解题意,分清已知与未知,
画出示意图(2)建模:根据已知条件与求解目标,把
已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型(3)求解:利用正弦定理或余弦定理有序地
解出三角形,求得数学模型的解(4)检验:检验上述所求的解是否符合实际
意义,从而得出实际问题的解 练习1.一艘船以32.2n mile / h的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向,30min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 已知△ABC中AB=1.95m,AC=1.40m,夹角∠CAB=66°20′,求BC.解:由余弦定理,得答:顶杆BC约长1.89m。 例3 .设AB是一个底部不可到达的竖直建筑物,A为建筑物的最高点,如何测量和计算建筑物AB的高度.CABEHG设在点C、D处测得A的仰角分别为α、β,CD=a,测角仪器的高度为h,试求建筑物高度AB.CABEHG问题探究D如图,在山顶上有一座铁塔BC,塔顶和塔底都可到达,A为地面上一点,通过测量哪些数据,可以计算出山顶的高度?设在点A处测得点B、C的仰角分别为α、β,铁塔的高BC=a,测角仪的高度忽略不计,试求山顶高度CD .问题解决例4.在山顶铁塔上B处测得地面上
一点A的俯角a =54°40′,在塔
底C处测得A处的俯角b =50°1′。
已知铁塔BC部分的高为27.3m,
求出山高CD(精确到1m)解:依题意可知,在△ABC中,
∠ABC=90o-a, ∠BAD=a , ∠CAD=b
∴∠BAC=a-b
∵根据正弦定理,1047m问题探究1.在测量上,根据测量需要适当确定的线段叫做基线.课堂小结2.距离测量问题包括一个不可到达点和两个不可到达点两种,设计测量方案的基本原则是:能够根据测量所得的数据计算所求两点间的距离,其中测量数据与基线的选取有关,计算时需要利用正、余弦定理.课堂小结3.解决物体高度测量问题时,一般先从一个或两个可到达点,测量出物体顶部或底部的仰角、俯角或方位角,再解三角形求相关数据.具体测量哪个类型的角,应根据实际情况而定.通常在地面测仰角,在空中测俯角,在行进中测方位角.课堂小结4.计算物体的高度时,一般先根据测量数据,利用正弦定理或余弦定理计算出物体顶部或底部到一个可到达点的距离,再解直角三角形求高度.150m补充练习 2 如图,有大小两座塔AB和CD,小塔的高为h,在小塔的底部A和顶部B测得另一塔顶D的仰角分别为α、β,求塔CD的高度.3 .飞机的海拔飞行高度是可知的,若飞机的航线和山顶在同一个铅垂平面内,飞机在水平飞行中测量山顶的高度,关键是求出哪个数据?飞机与山顶的海拔差 问题探究如图,设飞机在飞临山顶前,在B、C两处测得山顶A的俯角分别是α、β,B、C两点的飞行距离为a,飞机的海拔飞行高度是H,试求山顶的海拔高度h .作业:学海第4课时例题讲解 练1 在△ABC中,内角A,B,C对边的
边长分别是a,b,c.已知 (1)若△ABC的面积等于 ,求a,b. (2)sinC+sin(B-A)=2sin2A,求△ABC的面积.作业
