二次函数图像和性质复习课件

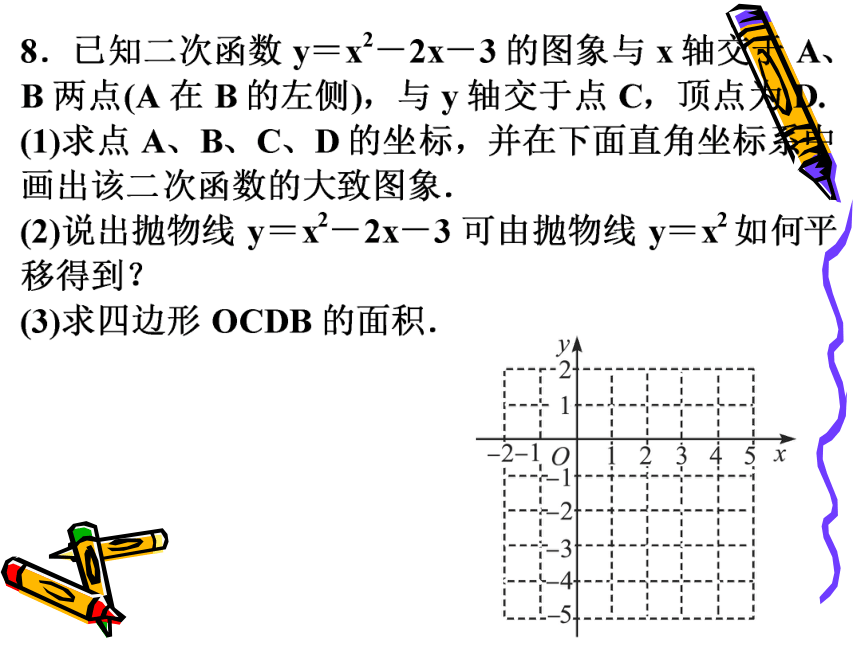
课件20张PPT。　二次函数图像和性质复习 例1：已知二次函数y=x2-2x-8
(1)二次项，一次项系数，常数
(2)求二次函数的顶点坐标，对称轴，最值
(3)当x在什么范围内，y随x的增大而减小
(4)当x为何值时，y＞0，x为何值时，y＜0
(5)把二次函数y=x2-2x-8向左平移三个单位，再向下平移四个单位得到函数解析式是什么？
二次函数的图象和基本性质例1：已知二次函数y=x2-2x-8
(6)若函数与x轴两个交点为A，B，与y轴的交点为C，求△ABC的面积，若函数的顶点为P，求△ABP的面积。
(7)二次函数y=x2-2x-8与二次函数 关于y轴对称。
(8)化二次函数y=x2-2x-8为顶点式和两根式。
例2.二次函数y=x2+bx+2
(1)若顶点在x轴上，则b=
(2)若顶点在y轴上，则b=
(3)若二次函数的最小值为1，则b=
(4)若二次函数在x=1时，有最小值，则b=
(5)若二次函数经过（1，0），则b=
例3（1）.y=6(x-1)(x+7)的对称轴是 最小值是 .
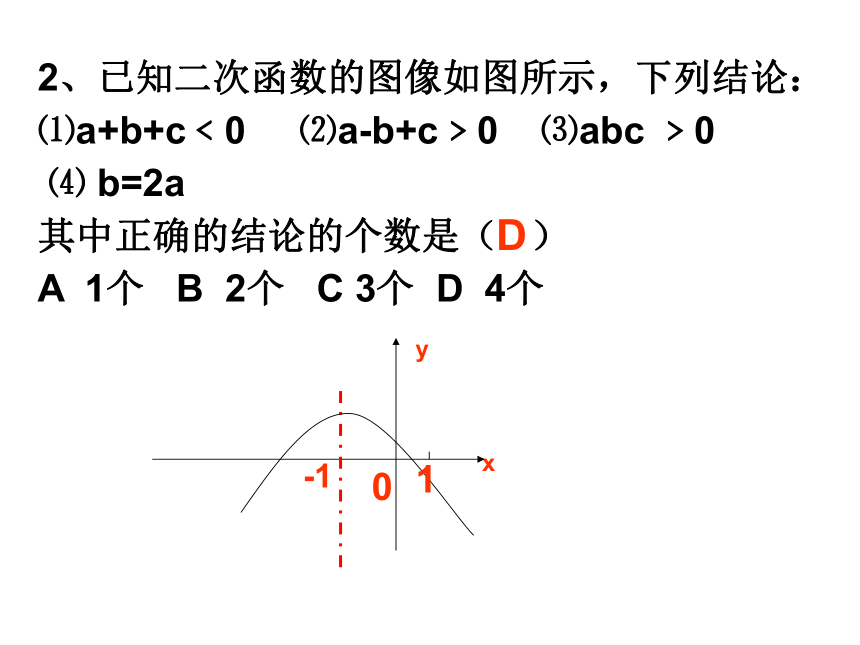
（2）若（-3，5）和（7，5）是某个二次函数上两点，则此 二次函数的对称轴是 .练习：2、已知二次函数的图像如图所示，下列结论：
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0
⑷ b=2a
其中正确的结论的个数是（ ）
A 1个 B 2个 C 3个 D 4个D练一练：3、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中下正确的是（）
A、abc＞0
B、b2-4ac＞0
C、2a+b＞0
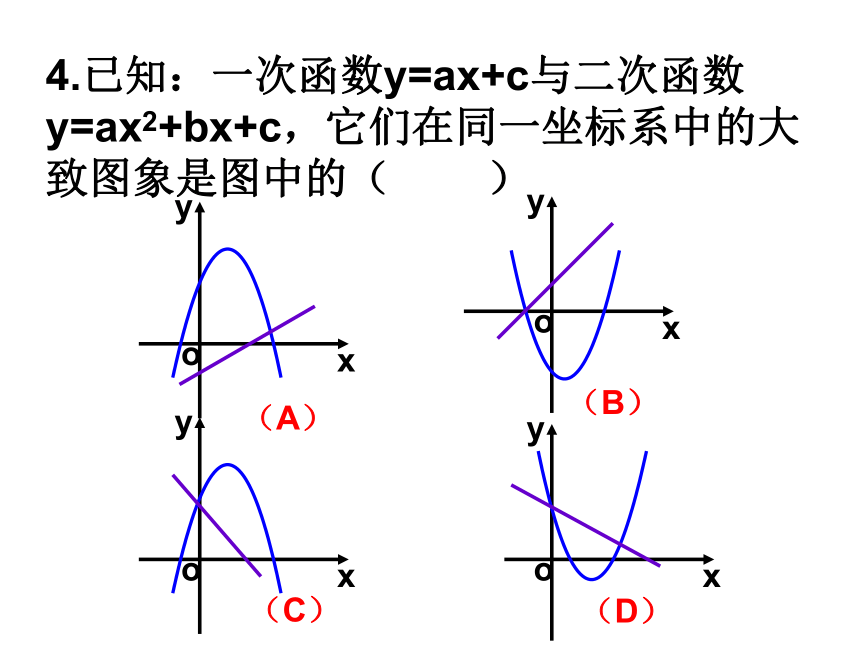
D、4a-2b+c＜04.已知：一次函数y=ax+c与二次函数y=ax2+bx+c，它们在同一坐标系中的大致图象是图中的（ ）（A）（B）（C）（D）6. 有一块铁皮拱形边缘呈抛物线状, MN=4，抛
物线的顶点处到MN的距离是 4，要 在 铁皮上截
下一矩形ABCD，是矩形的顶点B、C落在 MN 上，点A、D 落在抛物线上，问这样截下去的矩形铁皮的周长能否等于 8，若能，求出矩形的长和宽。若不能，说明理由。07.如图，等腰Rt△ABC的直角边AB＝２，点P、Q分别从A、C两点同时出发，以相等的速度作直线运动，已知点P沿射线AB运动，点Q沿边BC的延长线运动，PQ与直线AC相交于点D。
(1)设 AP的长为x，△PCQ的面积为S，
求出S关于x的函数关系式；
(2)当AP的长为何值时，
S△PCQ= S△ABC 1、二次函数y=ax2+bx+c(a≠0)的图象如图所示，
则a、b、c、△的符号为__________.　　　　　　尝试成功：2、已知二次函数的图像如图所示，下列结论：
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是（ ）A 1个 B 2个 C 3个 D 4个Dx-110y要点：寻求思路时，要着重观察抛物线的开口方向，对称轴，顶点的位置，抛物线与x轴、y轴的交点的位置，注意运用数形结合的思想。（一）抛物线解析式的三种方法练习　根据下列条件，求二次函数的解析式。(1)、图象经过(0，0)， (1，-2) ， (2，3) 三点；(2)、图象的顶点(2，3)， 且经过点(3，1) ；(3)、图象经过(0，0)， (12，0) ，且最高点
的纵坐标是3 。练习一：一座拱桥的示意图如图，当水面宽12m时，桥洞顶部离水面4m。已知桥洞的拱形是抛物线，要求该抛物线的函数解析式，你认为首先要做的工作是什么？如果以水平方向为x轴，取以下三个不同的点为坐标原点：
（1）点A，（2）点B，（3）抛物线的顶点C得的函数解析式相同吗？请试一试。哪种取法求得的函数解析式最简单？二次函数的应用