湘教版七年级数学上册课件:2.5 整式的加法和减法 (共14张PPT)
文档属性
| 名称 | 湘教版七年级数学上册课件:2.5 整式的加法和减法 (共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 752.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-09 07:25:04 | ||
图片预览






文档简介
课件14张PPT。2.5 整式的加法和减法1.理解同类项的概念,会识别同类项;
2.理解合并同类项的理论依据是三个运算定律(即加法交换律、结合律、乘法对加法的分配律)的使用;
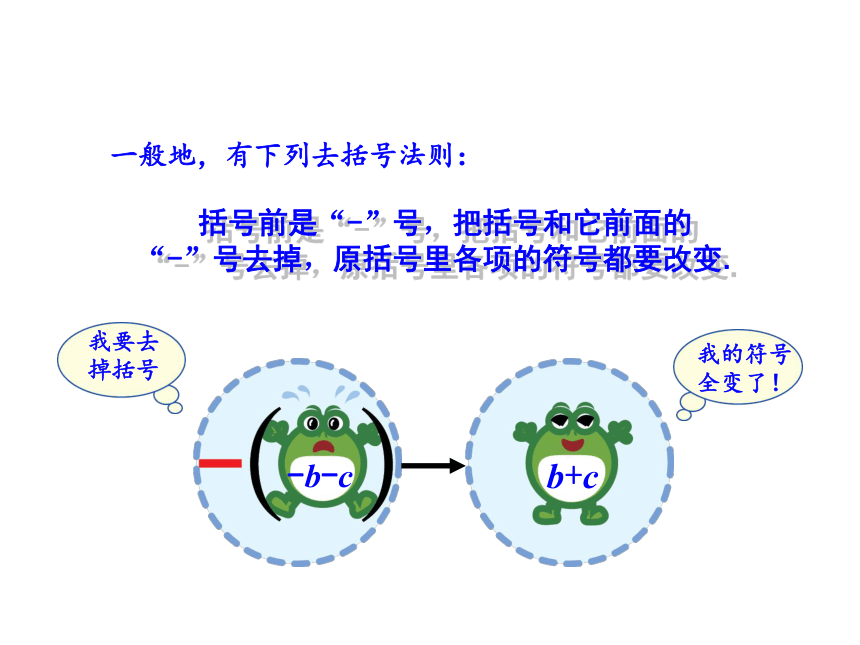
3.会把一个多项式中的同类项合并. 如图,在一块长为x,宽为y的草地中间,挖了一个面积为 的水池后,剩余草地的面积是多少? 例如在多项式x2y+3x+1-4x-5x2y -5中,同类项有x2y与-5x2y,3x与-4x,1与-5. 像多项式 中的项xy, ,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项. 把多项式中的同类项合并成一项,叫做合并同类项. 合并同类项时,只要把它们的系数相加,字母和字母的指数不变.一般地,有下列去括号法则:-b-c我要去
掉括号我的符号
全变了!b+c 括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要改变.例 合并同类项:
(1)-3x2-14x-5x2+4x2 ;
(2)xy3+x3y-2xy3+5x3y+9 .解(1) -3x2 -14x -5x2 + 4x2找同类项-3x2 -14x= (-3-5 + 4)x2 - 14x将同类项放在一起=合并同类项-3x2-14x= -4x2 -14x-5x2-5x2+ 4x2+ 4x2解(2) xy3+x3y-2xy3+5x3y+9找同类项= (1-2)xy3+(1+5)x3y+9将同类项放在一起=合并同类项xy3 + x3y -2xy3 + 5x3y + 9xy3+ x3y-2xy3+ 5x3y+ 9= -xy3+6x3y+91. 请将下面的同类项用线连接起来:随堂练习2. 合并同类项:(1)6x5-x5+9x5 ;
(2)-xy-4xy-7xy ;
(3)8x4y -6x4y +15xy+9-2x4y.解(1) 6x5-x5+9x5
= 5x5+9x2
= 14x5(2) -xy-4xy-7xy
= -5xy-7xy
= -12xy(3) 8x4y-6x4y +15xy+9-2x4y
= 8x4y-6x4y-2x4y+15xy+9
= 15xy+9 多项式的加减运算关键是正确地去括号、合并同类项. 去括号时,特别要注意括号前面如果是“-”号,则去掉括号后,括号里各项都要改变符号. 数学是一种理性的精神,使人类的思维得以运用到最完善的程度. ——克莱因
2.理解合并同类项的理论依据是三个运算定律(即加法交换律、结合律、乘法对加法的分配律)的使用;
3.会把一个多项式中的同类项合并. 如图,在一块长为x,宽为y的草地中间,挖了一个面积为 的水池后,剩余草地的面积是多少? 例如在多项式x2y+3x+1-4x-5x2y -5中,同类项有x2y与-5x2y,3x与-4x,1与-5. 像多项式 中的项xy, ,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项. 把多项式中的同类项合并成一项,叫做合并同类项. 合并同类项时,只要把它们的系数相加,字母和字母的指数不变.一般地,有下列去括号法则:-b-c我要去
掉括号我的符号
全变了!b+c 括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要改变.例 合并同类项:
(1)-3x2-14x-5x2+4x2 ;
(2)xy3+x3y-2xy3+5x3y+9 .解(1) -3x2 -14x -5x2 + 4x2找同类项-3x2 -14x= (-3-5 + 4)x2 - 14x将同类项放在一起=合并同类项-3x2-14x= -4x2 -14x-5x2-5x2+ 4x2+ 4x2解(2) xy3+x3y-2xy3+5x3y+9找同类项= (1-2)xy3+(1+5)x3y+9将同类项放在一起=合并同类项xy3 + x3y -2xy3 + 5x3y + 9xy3+ x3y-2xy3+ 5x3y+ 9= -xy3+6x3y+91. 请将下面的同类项用线连接起来:随堂练习2. 合并同类项:(1)6x5-x5+9x5 ;
(2)-xy-4xy-7xy ;
(3)8x4y -6x4y +15xy+9-2x4y.解(1) 6x5-x5+9x5
= 5x5+9x2
= 14x5(2) -xy-4xy-7xy
= -5xy-7xy
= -12xy(3) 8x4y-6x4y +15xy+9-2x4y
= 8x4y-6x4y-2x4y+15xy+9
= 15xy+9 多项式的加减运算关键是正确地去括号、合并同类项. 去括号时,特别要注意括号前面如果是“-”号,则去掉括号后,括号里各项都要改变符号. 数学是一种理性的精神,使人类的思维得以运用到最完善的程度. ——克莱因
同课章节目录
