湘教版七年级数学上册课件:3.4 一元一次方程模型的应用
文档属性
| 名称 | 湘教版七年级数学上册课件:3.4 一元一次方程模型的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 621.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-09 00:00:00 | ||
图片预览




文档简介
课件12张PPT。3.4 一元一次方程模型的应用1.通过教学,使学生了解应用题的一个重要步骤,是根据题意找出相等关系,然后列出方程.关键在于分析已知、未知量之间关系及寻找相等关系;
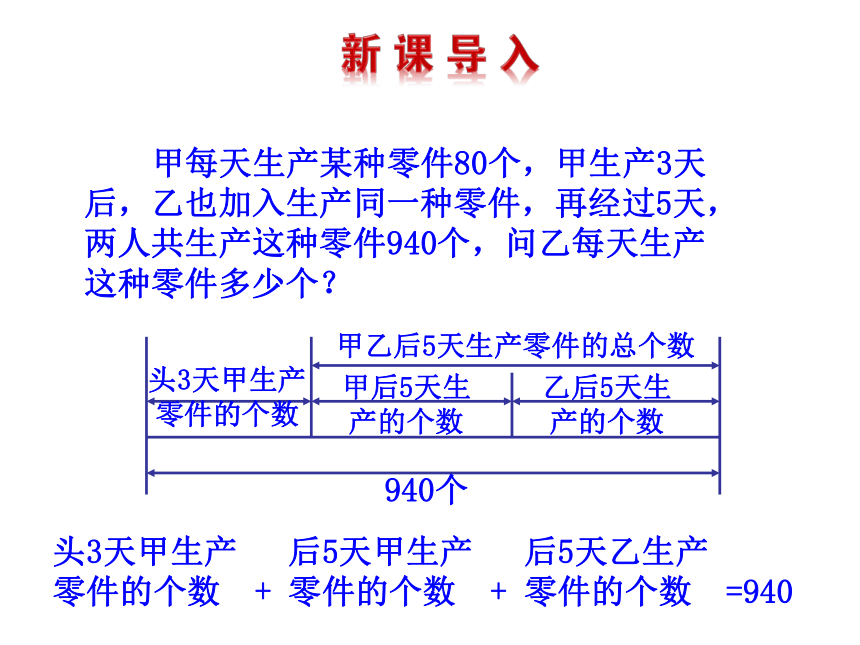
2.通过和、差、倍、分的量与量之间的分析,列出一元一次方程解简单的应用题. 甲每天生产某种零件80个,甲生产3天
后,乙也加入生产同一种零件,再经过5天,
两人共生产这种零件940个,问乙每天生产
这种零件多少个?头3天甲生产
零件的个数甲乙后5天生产零件的总个数甲后5天生
产的个数乙后5天生
产的个数940个头3天甲生产 后5天甲生产 后5天乙生产
零件的个数 + 零件的个数 + 零件的个数 =940解 设乙每天生产零件 X个.根据题意,得
解这个方程,得 X=60.
答:乙每天生产零件60个.头3天甲生产 后5天甲生产 后5天乙生产
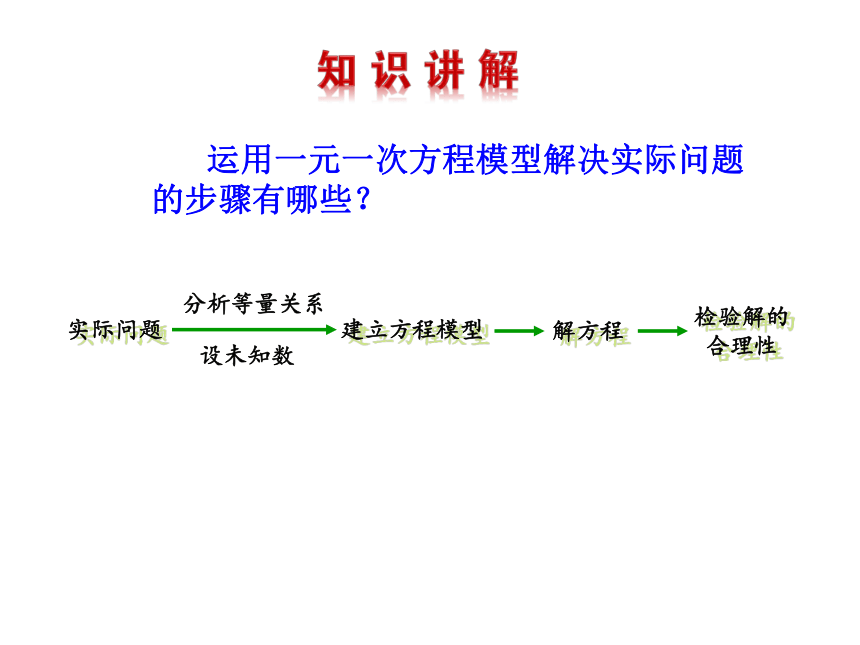
零件的个数 + 零件的个数 + 零件的个数 =940根据这一相等关系,设乙每天生产零件 X个,就可以列出方程. 运用一元一次方程模型解决实际问题的步骤有哪些?实际问题建立方程模型解方程检验解的
合理性例1 某房间里有四条腿的椅子和三条腿的凳子共16个,如果椅子腿数与凳子腿数的和为60条,有几张椅子和几条凳子?分析 本问题中涉及的等量关系有:
椅子数+凳子数=16,
椅子腿数+凳子腿数=60.解 设有x 张椅子,则有(16-x)条凳子.根据题意,得4x+ 3(16-x)=60 .去括号,得 4x+48-3x=60 .移项,合并同类项,得 x = 12 .凳子数为16-12=4(条).答:有12张椅子,4条凳子.例2 2011年10月1日,杨明将一笔钱存入某银行,定期 3年,年利率是5%. 若到期后取出,他可得本息和 23000元,求杨明存入的本金是多少元.解 设杨明存入的本金是 x 元,化简,得 1.15x = 23000.根据等量关系,得
x+3×5 % x = 23000,解得 x = 20000.答:杨明存入的本金是20000元.某百货商场元旦促销,购物不超过200元不优惠;超过200元,不足500元打9折;超过500元,其中500元打9折,超过部分打8折。某人这天两次购物分别用了110元和441元.
(1) 此人两次购物,如果其物品不打折,需要支付多少钱? (2)在此次活动中,他节省了多少钱?
(3)如果同一天你到这家百货商场购买同样的货物,你会采取怎样的购买方案?并请求出你省下的钱数.解:(1)如果不打折,需要支付 600元.(2)在此次活动中,他节省了49元钱.(3)我将一次性买齐所有货物,这样可以节省70元钱.随堂练习1.本节课学习了哪些内容?
2.列一元一次方程解应用题的方法和步骤是什么?
3.在运用上述方法和步骤时应注意什么? 在数学中,我们发现真理的主要工具是归纳和模拟. —— 拉普拉斯
2.通过和、差、倍、分的量与量之间的分析,列出一元一次方程解简单的应用题. 甲每天生产某种零件80个,甲生产3天
后,乙也加入生产同一种零件,再经过5天,
两人共生产这种零件940个,问乙每天生产
这种零件多少个?头3天甲生产
零件的个数甲乙后5天生产零件的总个数甲后5天生
产的个数乙后5天生
产的个数940个头3天甲生产 后5天甲生产 后5天乙生产
零件的个数 + 零件的个数 + 零件的个数 =940解 设乙每天生产零件 X个.根据题意,得
解这个方程,得 X=60.
答:乙每天生产零件60个.头3天甲生产 后5天甲生产 后5天乙生产
零件的个数 + 零件的个数 + 零件的个数 =940根据这一相等关系,设乙每天生产零件 X个,就可以列出方程. 运用一元一次方程模型解决实际问题的步骤有哪些?实际问题建立方程模型解方程检验解的
合理性例1 某房间里有四条腿的椅子和三条腿的凳子共16个,如果椅子腿数与凳子腿数的和为60条,有几张椅子和几条凳子?分析 本问题中涉及的等量关系有:
椅子数+凳子数=16,
椅子腿数+凳子腿数=60.解 设有x 张椅子,则有(16-x)条凳子.根据题意,得4x+ 3(16-x)=60 .去括号,得 4x+48-3x=60 .移项,合并同类项,得 x = 12 .凳子数为16-12=4(条).答:有12张椅子,4条凳子.例2 2011年10月1日,杨明将一笔钱存入某银行,定期 3年,年利率是5%. 若到期后取出,他可得本息和 23000元,求杨明存入的本金是多少元.解 设杨明存入的本金是 x 元,化简,得 1.15x = 23000.根据等量关系,得
x+3×5 % x = 23000,解得 x = 20000.答:杨明存入的本金是20000元.某百货商场元旦促销,购物不超过200元不优惠;超过200元,不足500元打9折;超过500元,其中500元打9折,超过部分打8折。某人这天两次购物分别用了110元和441元.
(1) 此人两次购物,如果其物品不打折,需要支付多少钱? (2)在此次活动中,他节省了多少钱?
(3)如果同一天你到这家百货商场购买同样的货物,你会采取怎样的购买方案?并请求出你省下的钱数.解:(1)如果不打折,需要支付 600元.(2)在此次活动中,他节省了49元钱.(3)我将一次性买齐所有货物,这样可以节省70元钱.随堂练习1.本节课学习了哪些内容?
2.列一元一次方程解应用题的方法和步骤是什么?
3.在运用上述方法和步骤时应注意什么? 在数学中,我们发现真理的主要工具是归纳和模拟. —— 拉普拉斯
同课章节目录
