3.3.2简单的线性规划问题(第二课时)
文档属性
| 名称 | 3.3.2简单的线性规划问题(第二课时) |  | |
| 格式 | rar | ||
| 文件大小 | 98.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-21 08:09:00 | ||
图片预览






文档简介
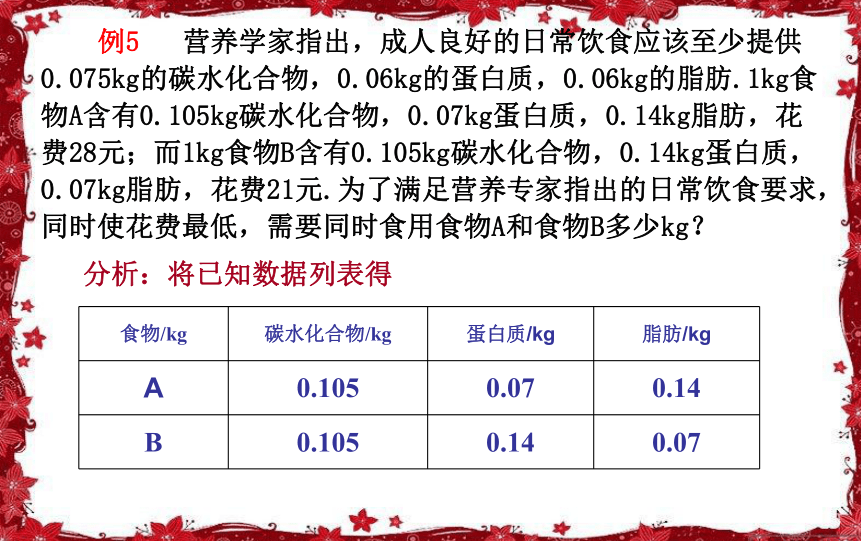
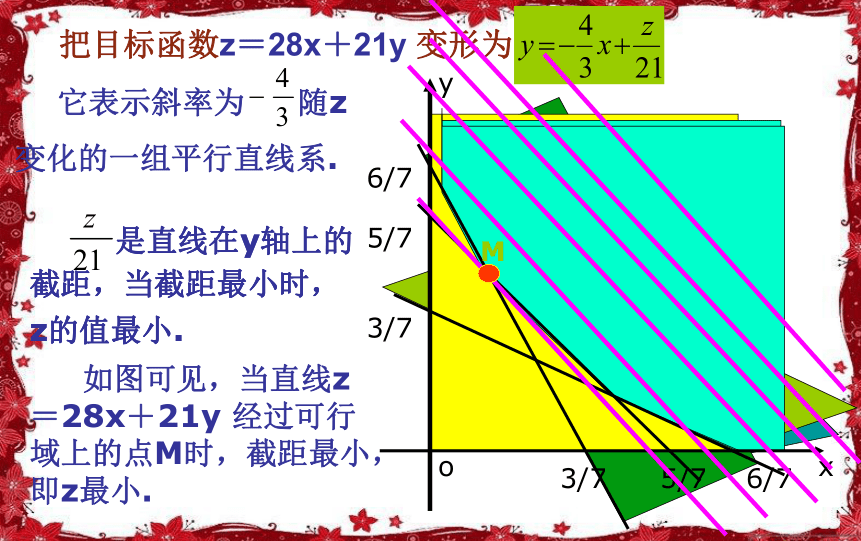
课件21张PPT。第二课时3.3.2 简单的线性规划问题复习回顾 1.二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域(虚线表示区域不包括边界直线). 2.线性规划的有关概念: 线性约束条件:不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件. 线性规划:在线性约束条件下求线性目标函数的最大值或最小值的问题,统称为线性规划问题. 可行域 :由所有可行解组成的集合叫做可行域;可行解 :满足线性约束条件的解(x,y)叫可行解; 最优解 :使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.线性规划在实际中的应用: 线性规划的理论和方法主要在两类问题中得到应用,一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务;二是给定一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务.下面我们就来看看线性规划在实际中的一些应用:分析:将已知数据列表得 例5 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪.1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?解:设每天食用xkg食物A,ykg食物B,总成本为z.那么目标函数为z=28x+21y作出二元一次不等式组所表示的可行域,如图:把目标函数z=28x+21y 变形为xyo5/75/76/73/73/76/7 它表示斜率为 随z
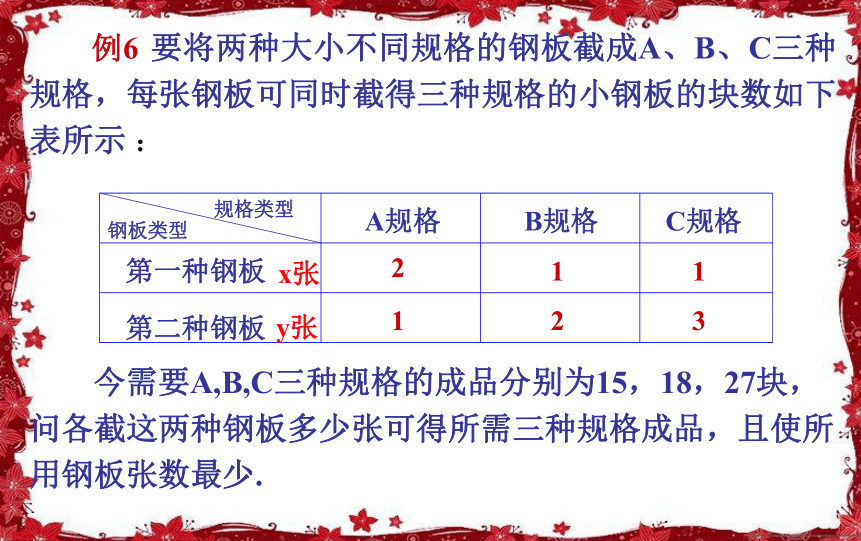
变化的一组平行直线系. 是直线在y轴上的截距,当截距最小时,z的值最小.M 如图可见,当直线z=28x+21y 经过可行域上的点M时,截距最小,即z最小. 是直线在y轴上的截距,当截距最小时,z的值最小.M点是两条直线的交点,解方程组 答:每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.得M点的坐标为:所以zmin=28x+21y= 说明:要完成一项确定的任务,如何统筹安排,尽量做到用最少的资源去完成它,这是线性规划中最常见的问题之一. 例6 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少.x张y张 解:设需截第一种钢板x张,第二种钢板y张,共需截这两张钢板共z张,则目标函数为z=x+y.线性约束条件为:2x+y=15x+3y=27x+2y=18x+y =0直线y=-x+12经过的整点是B(3,9)和C(4,8),它们是最优解. 作出一组平行直线y=-x+z,目标函数z= x+y当直线经过点A时z=x+y=11.4最小,x+y=12法一:调整优值法246181282724681015但它不是最优整数解.作直线y=-x+12答(略)2x+y=15x+3y=27x+2y=18x+y =0作出一组平行直线 z = x+y.目标函数z= x+y法二:打网格线法在可行域内打出网格线.当直线经过点A时 z=x+y=11.4,但它不是最优整数解, 将直线x+y=11.4继续向上平移,经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.作出可行域 答:要截得所需三种规格的钢板,且使所截两种钢板张数最小的方法有两种,第一种截法是截第一种钢板3张,第二种钢板9张;第二种截法是截第一种钢板4张,第二种钢板8张.两张钢板共12张. 说明:资源数量一定,如何安排使用它们,使得效益最好,这是线性规划中常见的问题之一. 结合上述两例子总结归纳一下解决这类问题的思路和方法: 简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的:(1)寻找线性约束条件,线性目标函数;(2)由二元一次不等式表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解.课堂练习课本第91页练习2课时小结用图解法解决简单的线性规划问题的基本步骤: 首先,应准确建立数学模型,即根据题意找出约束条件,确定线性目标函数. 然后,用图解法求得数学模型的解,即画出可行域,在可行域内求得使目标函数取得最值的解. 最后,要根据实际意义将数学模型的解转化为实际问题的解,即结合实际情况求得最优解. 作业课本第93页习题[A]组的第4题.补充练习 1.某家具厂有方木材90m3,木工板600m3,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、木工板2m3;生产每个书橱需要方木料0.2m3,木工板1m3,出售一张书桌可以获利80元,出售一张书橱可以获利120元;(1)怎样安排生产可以获利最大?(2)若只生产书桌可以获利多少?(3)若只生产书橱可以获利多少?由上表可知:
(1)只生产书桌,用完木工板了,可生产书桌 600÷2=300张,可获利润:80×300=24000元,但木料没有用完 (2)只生产书橱,用完方木料,可生产书橱90÷0.2=450 张,可获利润120×450=54000元,但木工板没有用完分析:300600A(100,400) 1.某家具厂有方木材90m3,木工板600m3,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、木工板2m3;生产每个书橱需要方木料0.2m3,木工板1m3,出售一张书桌可以获利80元,出售一张书橱可以获利120元;(1)怎样安排生产可以获利最大?(2)若只生产书桌可以获利多少?(3)若只生产书橱可以获利多少?(1)设生产书桌x张,书橱y张,利润为z元, 则约束条件为 Z=80x+120y作出不等式表示的平面区域,当生产100张书桌,400张书橱时利润最大为z=80×100+120×400=56000元(2)若只生产书桌可以生产300张,用完木工板,可获利 24000元;(3)若只生产书橱可以生产450张,用完方木料,可获利54000元。将直线z=80x+120y平移可知:900450求解:4x=8y=4x+y=104x+5y=30320x+504y=0 2.某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重量为6吨的A型卡车和4辆载重量为10吨的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的成本费A型卡车为320元,B型卡车为504元,问如何安排车辆才能使该公司所花的成本费最低,最低为多少元?(要求每型卡车至少安排一辆)解:设每天调出的A型车x辆,B型车y辆,公司所花的费用为z元,则Z=320x+504y作出可行域中的整点,可行域中的整点(5,2)使Z=320x+504y取得最小值,且Zmin=2608元作出可行域
变化的一组平行直线系. 是直线在y轴上的截距,当截距最小时,z的值最小.M 如图可见,当直线z=28x+21y 经过可行域上的点M时,截距最小,即z最小. 是直线在y轴上的截距,当截距最小时,z的值最小.M点是两条直线的交点,解方程组 答:每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.得M点的坐标为:所以zmin=28x+21y= 说明:要完成一项确定的任务,如何统筹安排,尽量做到用最少的资源去完成它,这是线性规划中最常见的问题之一. 例6 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少.x张y张 解:设需截第一种钢板x张,第二种钢板y张,共需截这两张钢板共z张,则目标函数为z=x+y.线性约束条件为:2x+y=15x+3y=27x+2y=18x+y =0直线y=-x+12经过的整点是B(3,9)和C(4,8),它们是最优解. 作出一组平行直线y=-x+z,目标函数z= x+y当直线经过点A时z=x+y=11.4最小,x+y=12法一:调整优值法246181282724681015但它不是最优整数解.作直线y=-x+12答(略)2x+y=15x+3y=27x+2y=18x+y =0作出一组平行直线 z = x+y.目标函数z= x+y法二:打网格线法在可行域内打出网格线.当直线经过点A时 z=x+y=11.4,但它不是最优整数解, 将直线x+y=11.4继续向上平移,经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.作出可行域 答:要截得所需三种规格的钢板,且使所截两种钢板张数最小的方法有两种,第一种截法是截第一种钢板3张,第二种钢板9张;第二种截法是截第一种钢板4张,第二种钢板8张.两张钢板共12张. 说明:资源数量一定,如何安排使用它们,使得效益最好,这是线性规划中常见的问题之一. 结合上述两例子总结归纳一下解决这类问题的思路和方法: 简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的:(1)寻找线性约束条件,线性目标函数;(2)由二元一次不等式表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解.课堂练习课本第91页练习2课时小结用图解法解决简单的线性规划问题的基本步骤: 首先,应准确建立数学模型,即根据题意找出约束条件,确定线性目标函数. 然后,用图解法求得数学模型的解,即画出可行域,在可行域内求得使目标函数取得最值的解. 最后,要根据实际意义将数学模型的解转化为实际问题的解,即结合实际情况求得最优解. 作业课本第93页习题[A]组的第4题.补充练习 1.某家具厂有方木材90m3,木工板600m3,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、木工板2m3;生产每个书橱需要方木料0.2m3,木工板1m3,出售一张书桌可以获利80元,出售一张书橱可以获利120元;(1)怎样安排生产可以获利最大?(2)若只生产书桌可以获利多少?(3)若只生产书橱可以获利多少?由上表可知:
(1)只生产书桌,用完木工板了,可生产书桌 600÷2=300张,可获利润:80×300=24000元,但木料没有用完 (2)只生产书橱,用完方木料,可生产书橱90÷0.2=450 张,可获利润120×450=54000元,但木工板没有用完分析:300600A(100,400) 1.某家具厂有方木材90m3,木工板600m3,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、木工板2m3;生产每个书橱需要方木料0.2m3,木工板1m3,出售一张书桌可以获利80元,出售一张书橱可以获利120元;(1)怎样安排生产可以获利最大?(2)若只生产书桌可以获利多少?(3)若只生产书橱可以获利多少?(1)设生产书桌x张,书橱y张,利润为z元, 则约束条件为 Z=80x+120y作出不等式表示的平面区域,当生产100张书桌,400张书橱时利润最大为z=80×100+120×400=56000元(2)若只生产书桌可以生产300张,用完木工板,可获利 24000元;(3)若只生产书橱可以生产450张,用完方木料,可获利54000元。将直线z=80x+120y平移可知:900450求解:4x=8y=4x+y=104x+5y=30320x+504y=0 2.某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重量为6吨的A型卡车和4辆载重量为10吨的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的成本费A型卡车为320元,B型卡车为504元,问如何安排车辆才能使该公司所花的成本费最低,最低为多少元?(要求每型卡车至少安排一辆)解:设每天调出的A型车x辆,B型车y辆,公司所花的费用为z元,则Z=320x+504y作出可行域中的整点,可行域中的整点(5,2)使Z=320x+504y取得最小值,且Zmin=2608元作出可行域
