高中物理选修3-1习题课件:第1章《静电场》 (共24张PPT)
文档属性
| 名称 | 高中物理选修3-1习题课件:第1章《静电场》 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-10-09 22:22:11 | ||
图片预览




文档简介
课件24张PPT。静电场答案一、选择题1.(0388)
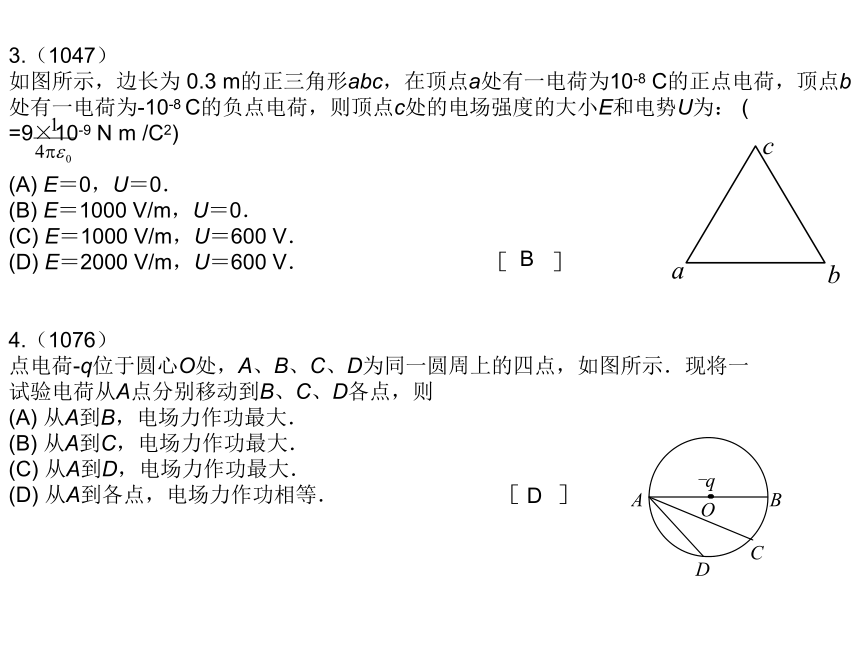
在坐标原点放一正电荷Q,它在P点(x=+1,y=0)产生的电场强度为 .现在,另外有一个负电荷-2Q,试问应将它放在什么位置才能使P点的电场强度等于零?
(A) x轴上x>1. (B) x轴上0 (C) x轴上x<0. (D) y轴上y>0.
(E) y轴上y<0. [ ]2.(1034)
有两个电荷都是+q 的点电荷,相距为2a.今以左边的点电荷所在处为球心,以a为半径作一球形高斯面 . 在球面上取两块相等的小面积S1和S2,其位置如图所示. 设通过S1和S2的电场强度通量分别为φ1和φ2,通过整个球面的电场强度通量为φS,则
(A) φ1>φ2φS=q /ε0.
(B) φ1<φ2,φS=2q /ε0.
(C) φ1=φ2,φS=q /ε0.
(D) φ1<φ2,φS=q /ε0. [ ]C D 3.(1047)
如图所示,边长为 0.3 m的正三角形abc,在顶点a处有一电荷为10-8 C的正点电荷,顶点b处有一电荷为-10-8 C的负点电荷,则顶点c处的电场强度的大小E和电势U为: ( =9×10-9 N m /C2)
(A) E=0,U=0.
(B) E=1000 V/m,U=0.
(C) E=1000 V/m,U=600 V.
(D) E=2000 V/m,U=600 V. [ ]4.(1076)
点电荷-q位于圆心O处,A、B、C、D为同一圆周上的四点,如图所示.现将一试验电荷从A点分别移动到B、C、D各点,则
(A) 从A到B,电场力作功最大.
(B) 从A到C,电场力作功最大.
(C) 从A到D,电场力作功最大.
(D) 从A到各点,电场力作功相等. [ ] B D 二、填空题
1.(1042)
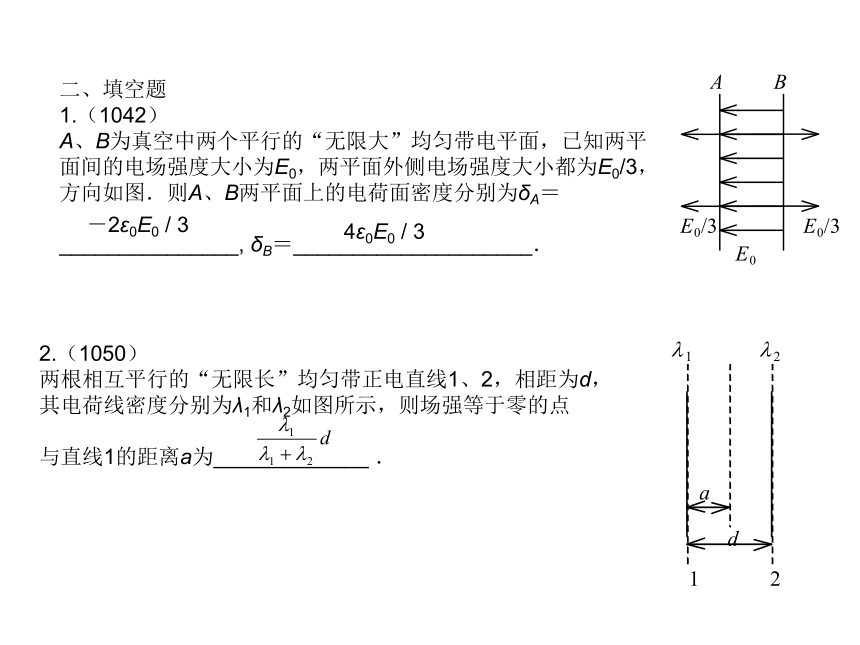
A、B为真空中两个平行的“无限大”均匀带电平面,已知两平面间的电场强度大小为E0,两平面外侧电场强度大小都为E0/3,方向如图.则A、B两平面上的电荷面密度分别为δA=
_______________, δB=____________________.2.(1050)
两根相互平行的“无限长”均匀带正电直线1、2,相距为d,其电荷线密度分别为λ1和λ2如图所示,则场强等于零的点
与直线1的距离a为_____________ .-2ε0E0 / 3 4ε0E0 / 3 3.(1498)
如图,点电荷q 和-q被包围在高斯面S内,则通过该高
斯面的电场强度通量 =_____________,式中
为_________________处的场强. 4.(1194)
把一个均匀带有电荷+Q的球形肥皂泡由半径r1吹胀到r2,则半径为R(r1<R<r2)的
球面上任一点的场强大小E由______________变为______________;电势U由
__________________________变为________________(选无穷远处为电势零点). 0 高斯面上各点 Q/(4πε0R2) Q/(4πε0R) 0 Q/(4πε0r2) 计算题
1.(1009)
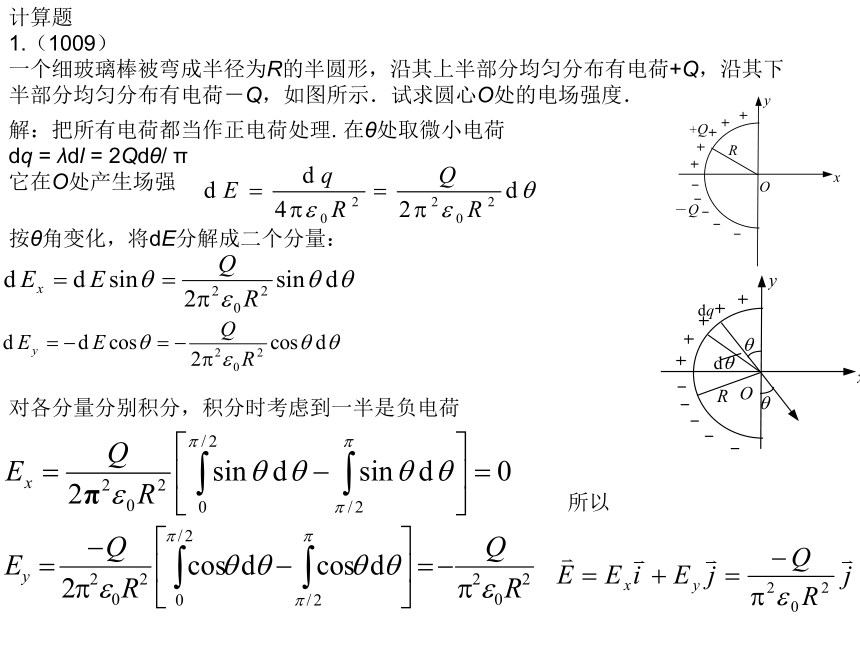
一个细玻璃棒被弯成半径为R的半圆形,沿其上半部分均匀分布有电荷+Q,沿其下半部分均匀分布有电荷-Q,如图所示.试求圆心O处的电场强度.解:把所有电荷都当作正电荷处理. 在θ处取微小电荷 dq = λdl = 2Qdθ/ π
它在O处产生场强按θ角变化,将dE分解成二个分量:对各分量分别积分,积分时考虑到一半是负电荷所以 2.(1010)
带电细线弯成半径为R的半圆形,电荷线密度为λ=λ0sinφ,式中λ0为一常数,φ为半径R与x轴所成的夹角,如图所示.试求环心O处的电场强度.解:在φ处取电荷元,其电荷为:
dq =λdl = λ0Rsinφ dφ它在O点产生的场强为 在x、y轴上的二个分量 对各分量分别求和 所以 3.(1059)
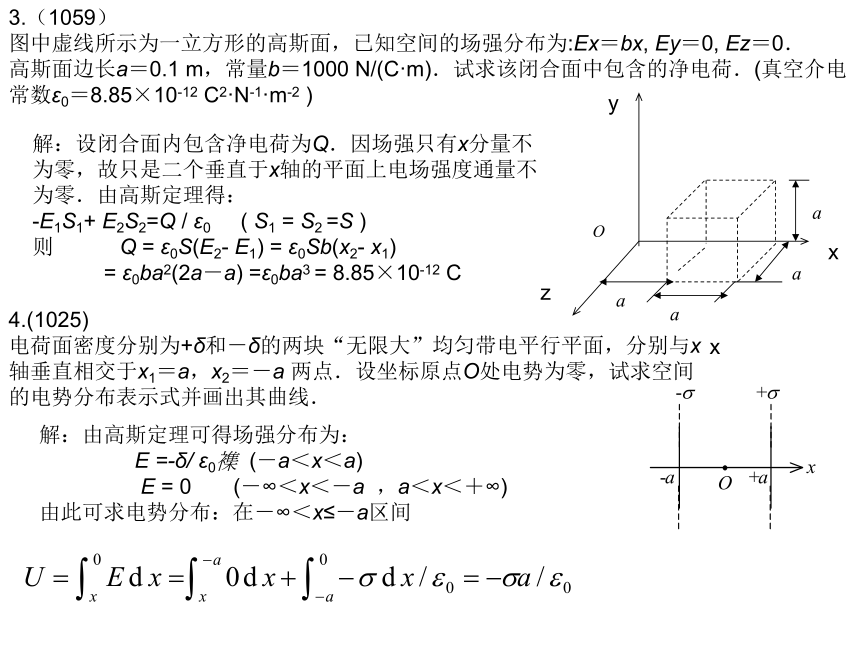
图中虚线所示为一立方形的高斯面,已知空间的场强分布为:Ex=bx, Ey=0, Ez=0.
高斯面边长a=0.1 m,常量b=1000 N/(C·m).试求该闭合面中包含的净电荷.(真空介电常数ε0=8.85×10-12 C2·N-1·m-2 )O ax解:设闭合面内包含净电荷为Q.因场强只有x分量不为零,故只是二个垂直于x轴的平面上电场强度通量不为零.由高斯定理得:
-E1S1+ E2S2=Q / ε0 ( S1 = S2 =S )
则 Q = ε0S(E2- E1) = ε0Sb(x2- x1)
= ε0ba2(2a-a) =ε0ba3 = 8.85×10-12 C 4.(1025)
电荷面密度分别为+δ和-δ的两块“无限大”均匀带电平行平面,分别与x轴垂直相交于x1=a,x2=-a 两点.设坐标原点O处电势为零,试求空间的电势分布表示式并画出其曲线. 解:由高斯定理可得场强分布为:
E =-δ/ ε0? (-a<x<a)
E = 0 (-∞<x<-a ,a<x<+∞)
由此可求电势分布:在-∞<x≤-a区间 在-a≤x≤a区间 在a≤x<∞区间 5.(1179)如图所示,两个点电荷+q 和-3q,相距为d. 试求:
(1) 在它们的连线上电场强度的点与电荷为+q 的点电荷相距多远?
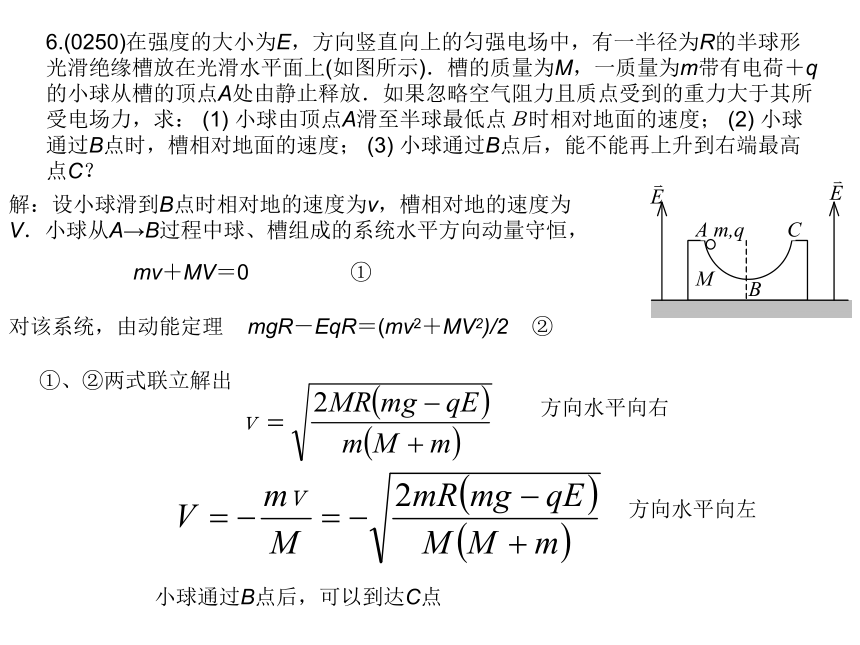
(2) 若选无穷远处电势为零,两点电荷之间电势U=0的点与电荷为+q的点电荷相距多远?解:设点电荷q所在处为坐标原点O,x轴沿两点电荷的连线 (1) 设的点的坐标为,则 另有一解不符合题意,舍去. (2) 设坐标x处U=0,则 得 d- 4x = 0, x = d/4 可得 解出 6.(0250)在强度的大小为E,方向竖直向上的匀强电场中,有一半径为R的半球形光滑绝缘槽放在光滑水平面上(如图所示).槽的质量为M,一质量为m带有电荷+q 的小球从槽的顶点A处由静止释放.如果忽略空气阻力且质点受到的重力大于其所受电场力,求: (1) 小球由顶点A滑至半球最低点B时相对地面的速度; (2) 小球通过B点时,槽相对地面的速度; (3) 小球通过B点后,能不能再上升到右端最高点C?解:设小球滑到B点时相对地的速度为v,槽相对地的速度为V.小球从A→B过程中球、槽组成的系统水平方向动量守恒, mv+MV=0 ① 对该系统,由动能定理 mgR-EqR=(mv2+MV2)/2 ② ①、②两式联立解出 方向水平向右 方向水平向左 小球通过B点后,可以到达C点 7.(1081)一均匀电场,场强大小为E=5×104 N/C,方向竖直朝上,把一电荷为q= 2.5×10-8 C的点电荷,置于此电场中的a点,如图所示.求此点电荷在下列过程中电场力作的功.
(1) 沿半圆路径Ⅰ移到右方同高度的b点, =45 cm;
(2) 沿直线路径Ⅱ向下移到c点, =80 cm;
(3) 沿曲线路径Ⅲ朝右斜上方向移到d点, =260 cm(与水平方向成45°角). 解:(1) (2) =-1×10-3 J (3) =2.3×10-3 J 8.(1276)
如图所示,三个“无限长”的同轴导体圆柱面A、B和C,半径分别为Ra、Rb、Rc.圆柱面B上带电荷,A和C都接地.求B的内表面上电荷线密度λ1和外表面上电荷线密度λ2之比值λ1/ λ2.解:设B上带正电荷,内表面上电荷线密度为λ1,外表面上电荷线密度为λ2,而A、C上相应地感应等量负电荷,如图所示.则A、B间场强分布为 E1=λ1 / 2πε0r,方向由B指向A B、C间场强分布为 E2=λ2 / 2πε0r,方向由B指向C B、A 间电势差 B、C 间电势差 因UBA=UBC ,得到 9.(1072)
在真空中一长为l=10 cm的细杆上均匀分布着电荷,其电荷线密度λ= 1.0×10-5 C/m.在杆的延长线上,距杆的一端距离d=10 cm的一点上,有一点电荷q0= 2.0×10-5 C,如图所示.试求该点电荷所受的电场力.(真空介电常量ε0=8.85×10-12 C2·N-1·m-2 )解:选杆的左端为坐标原点,x轴沿杆的方向 .在x处取一电荷元λdx,它在点电荷所在处产生场强为: 整个杆上电荷在该点的场强为: 点电荷q0所受的电场力为: =0.90 N 沿x轴负向 10.(1245)如图所示,有一高为h 的直角形光滑斜面, 斜面倾角为a.在直角顶点A处有一电荷为-q 的点电荷.另有一质量为m、电荷+q 的小球在斜面的顶点B 由静止下滑.设小球可看作质点,试求小球到达斜面底部C点时的速率. 解:因重力和电场力都是保守力,小球从顶点B 到达底部C点过程中能量守恒. ∴ 理论推导与证明1.(1265)真空中点电荷q的静电场场强大小为
式中r 为场点离点电荷的距离.当r→0时,E→∞,这一推论显然是没有物理意义的,应如何解释? 答:点电荷的场强公式仅适用于点电荷,当r→0时,任何带电体都不能视为点
电荷,所以点电荷场强公式已不适用.
若仍用此式求场强E,其结论必然是错误的.当r→0时,需要具体考虑带
电体的大小和电荷分布,这样求得的E就有确定值. 2.(1295)电荷为q1的一个点电荷处在一高斯球面的中心处,问在下列三种情况下,穿过此高斯面的电场强度通量是否会改变?电场强度通量各是多少?
(1) 将电荷为q2的第二个点电荷放在高斯面外的附近处;
(2) 将上述的q2放在高斯面内的任意处;
(3) 将原来的点电荷移离高斯面的球心,但仍在高斯面内答:根据高斯定理,穿过高斯面的电通量仅取决于面内电量的代数和,而与面内电荷的分布情况及面外电荷无关,故:
(1) 电通量不变, ?1=q1 / ε0;
(2) 电通量改变,由?1变为?2=(q1+q2 ) / ε0;
(3) 电通量不变,仍为?1. 静电场中电介质选择题1.(1137)有一接地的金属球,用一弹簧吊起,金属球原来不带电.若在它的下方放置一电荷为q 的点电荷,如图所示,则
(A) 只有当q > 0 时,金属球才下移.
(B) 只有当q < 0 时,金属球才下移.
(C) 无论q 是正是负金属球都下移.
(D) 无论q 是正是负金属球都不动. [ ]C 2.(1101)一导体球外充满相对介电常量为εr 的均匀电介质,若测得导体表面附近场强为E,则导体球面上的自由电荷面密度δ为
(A) ε 0 E. (B) ε 0 εr E.
(C) ε r E. (D) (ε 0 εr - ε 0)E. [ ] B 3.(1139)
一个大平行板电容器水平放置,两极板间的一半空间充有各向同性均匀电介质,另一半为空气,如图.当两极板带上恒定的等量异号电荷时,有一个质量为m、带电荷为+q 的质点,在极板间的空气区域中处于平衡.此后,若把电介质抽去 ,则该质点
(A) 保持不动. (B) 向上运动.
(C) 向下运动. (D) 是否运动不能确定. [ ] B 4.(1224)
一空气平行板电容器充电后与电源 断开,然后在两极板间充满某种各向同性、均匀电介质,则电场强度的大小E、电容C、电压U、电场能量W四个量各自与充入介质前相比较,增大(↑)或减小(↓)的情形为
(A) E↑,C↑,U↑,W↑.
(B) E↓,C↑,U↓,W↓.
(C) E↓,C↑,U↑,W↓.
(D) E↑,C↓,U↓,W↑. [ ] B 填空题1.(1152)
如图所示,把一块原来不带电的金属板B,移近一块已带有正电荷Q的金属板A,平行放置.设两板面积都是S,板间距离是d,忽略边缘效应.当B板不接地时,两板间
势差UAB =___________________ ;B 板接地时两板间电势差
__________ . 2.(1116)一空气平行板电容器,两极板间距为d,充电后板间电压为U.然后将电源断开,在两板间平行地插入一厚度为d/3的金属板,则板间电压变成
U' =________________ .2U/3 3.(1320)
一平行板电容器,两板间充满各向同性均匀电介质,已知相对介电常量为
εr .若极板上的自由电荷面密度为δ ,则介质中电位移的大小D
=____________,
电场强度的大小E =____________________. δ δ / ( ε 0ε r ) 4.(1237)
两个电容器1和2,串联以后接上电动势恒定的电源充电.在电源保持联接
的情况下,若把电介质充入电容器2中,则电容器1上的电势差______________;
电容器1极板上的电荷____________.(填增大、减小、不变) 增大 增大 5.(5107)
1、2是两个完全相同的空气电容器.将其充电后与电源断开,再将一块各向同性均匀电介质板插入电容器1的两极板间,如图所示, 则电容器2 的电压U2,电场能量W2如何变
化?(填增大,减小或不变) U2 _________,
W2 _____________. 减小 减小 计算题1.(5425)半径分别为R1和R2 (R2 > R1 )的两个同心导体薄球壳,分别带有电荷Q1和Q2,今将内球壳用细导线与远处半径为r 的导体球相联,如图所示, 导体球原来不带电,试求相联后导体球所带电荷q. 解:设导体球带电q,取无穷远处为电势零点,则
导体球电势: 内球壳电势: 二者等电势,即 解得 2.(1182)
一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半径分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量为εr 的各向同性、均匀电介质.电容器接在电压U = 32 V的电源上,(如图所示),试求距离轴线R = 3.5 cm处的A点的电场强度和A点与外筒间的电势差. 解:设内外圆筒沿轴向单位长度上分别带有电荷+? 和?? , 根据高斯定理可求得两圆筒间任一点的电场强度为 则两圆筒的电势差为 解得 于是可求得A点的电场强度为 = 998 V/m 方向沿径向向外 A点与外筒间的电势差: = 12.5 V 3.(5682)
一绝缘金属物体,在真空中充电达某一电势值,其电场总能量为W0.若断开电源,使其上所带电荷保持不变,并把它浸没在相对介电常量为εr 的无限大的各向同性均匀液态电介质中,问这时电场总能量有多大?解:因为所带电荷保持不变,故电场中各点的电位移矢量 保持不变, 又 因为介质均匀,∴电场总能量 4.(1489)半径分别为 1.0 cm与 2.0 cm 的两个球形导体,各带电荷 1.0×10-8 C,两球相 距很远.若用细导线将两球相连接.求(1) 每个球所带电荷;(2) 每球的电
势.( )解:两球相 距很远,可视为孤立导体,互不影响.球上电荷均匀分布.设两球半径分别为r1和r2,导线连接后的电荷分别为q1和q2,而q1 + q2 = 2q,则两球电势分别是 两球相连后电势相等, ,则有 由此得到 C C 两球电势 V 改错1.(1165)
同一种材料的导体A1、A2紧靠一起, 放在外电场中(图a).将A1、A2 分开后撤去电场(图b).下列说法是否正确? 如有错误请改正.
(1) 在图(a)中,A1 左端的电势比A2右端的电势低.
(2) 在图(b)中,A1 的电势比A2 的电势低 答:(1) 在图(a)中,A1 左端和A2 右端电势相等
(2) 正确. 2.(5117)
两块平行放置的无限大导体平板A 和B,面积均为S.A板带电荷为+Q (>0),B 板不带电.有人画出导体静电平衡时两板上的电荷分布如图所示.所画电荷分布是否正确如有错误,请指出,并画出正确的电荷分布图. 答:所画电荷分布不能使A、B两板内部场强为零,所以是错误的.
正确的电荷分布如右图所示. 问答题1.(1166)
有两个相距“无限远”的金属球,其中一个带正电荷Q,它在球外离球心为r 处的
一点电场强度为 ,另一金属球带负电荷Q2,它在球外离球心为r 的一点处
场强为 .当两球从“无限远”移近到两球心相 距为2 r 时,在球心连线中点
处的合场强为 ,你认为这一结果对吗?为什么? 答:结论是不对的!
当两金属球相距“无限远”时,两球上电荷是均匀分布的,在这样的情形下,所得
的场强为 和 .当两球靠近时,由于静电感应,两球上电荷不再均匀
分布.因而在两球连线中点处的场强已不再分别是 和 ,因而合场
强 了.
在坐标原点放一正电荷Q,它在P点(x=+1,y=0)产生的电场强度为 .现在,另外有一个负电荷-2Q,试问应将它放在什么位置才能使P点的电场强度等于零?
(A) x轴上x>1. (B) x轴上0
(E) y轴上y<0. [ ]2.(1034)
有两个电荷都是+q 的点电荷,相距为2a.今以左边的点电荷所在处为球心,以a为半径作一球形高斯面 . 在球面上取两块相等的小面积S1和S2,其位置如图所示. 设通过S1和S2的电场强度通量分别为φ1和φ2,通过整个球面的电场强度通量为φS,则
(A) φ1>φ2φS=q /ε0.
(B) φ1<φ2,φS=2q /ε0.
(C) φ1=φ2,φS=q /ε0.
(D) φ1<φ2,φS=q /ε0. [ ]C D 3.(1047)
如图所示,边长为 0.3 m的正三角形abc,在顶点a处有一电荷为10-8 C的正点电荷,顶点b处有一电荷为-10-8 C的负点电荷,则顶点c处的电场强度的大小E和电势U为: ( =9×10-9 N m /C2)
(A) E=0,U=0.
(B) E=1000 V/m,U=0.
(C) E=1000 V/m,U=600 V.
(D) E=2000 V/m,U=600 V. [ ]4.(1076)
点电荷-q位于圆心O处,A、B、C、D为同一圆周上的四点,如图所示.现将一试验电荷从A点分别移动到B、C、D各点,则
(A) 从A到B,电场力作功最大.
(B) 从A到C,电场力作功最大.
(C) 从A到D,电场力作功最大.
(D) 从A到各点,电场力作功相等. [ ] B D 二、填空题
1.(1042)
A、B为真空中两个平行的“无限大”均匀带电平面,已知两平面间的电场强度大小为E0,两平面外侧电场强度大小都为E0/3,方向如图.则A、B两平面上的电荷面密度分别为δA=
_______________, δB=____________________.2.(1050)
两根相互平行的“无限长”均匀带正电直线1、2,相距为d,其电荷线密度分别为λ1和λ2如图所示,则场强等于零的点
与直线1的距离a为_____________ .-2ε0E0 / 3 4ε0E0 / 3 3.(1498)
如图,点电荷q 和-q被包围在高斯面S内,则通过该高
斯面的电场强度通量 =_____________,式中
为_________________处的场强. 4.(1194)
把一个均匀带有电荷+Q的球形肥皂泡由半径r1吹胀到r2,则半径为R(r1<R<r2)的
球面上任一点的场强大小E由______________变为______________;电势U由
__________________________变为________________(选无穷远处为电势零点). 0 高斯面上各点 Q/(4πε0R2) Q/(4πε0R) 0 Q/(4πε0r2) 计算题
1.(1009)
一个细玻璃棒被弯成半径为R的半圆形,沿其上半部分均匀分布有电荷+Q,沿其下半部分均匀分布有电荷-Q,如图所示.试求圆心O处的电场强度.解:把所有电荷都当作正电荷处理. 在θ处取微小电荷 dq = λdl = 2Qdθ/ π
它在O处产生场强按θ角变化,将dE分解成二个分量:对各分量分别积分,积分时考虑到一半是负电荷所以 2.(1010)
带电细线弯成半径为R的半圆形,电荷线密度为λ=λ0sinφ,式中λ0为一常数,φ为半径R与x轴所成的夹角,如图所示.试求环心O处的电场强度.解:在φ处取电荷元,其电荷为:
dq =λdl = λ0Rsinφ dφ它在O点产生的场强为 在x、y轴上的二个分量 对各分量分别求和 所以 3.(1059)
图中虚线所示为一立方形的高斯面,已知空间的场强分布为:Ex=bx, Ey=0, Ez=0.
高斯面边长a=0.1 m,常量b=1000 N/(C·m).试求该闭合面中包含的净电荷.(真空介电常数ε0=8.85×10-12 C2·N-1·m-2 )O ax解:设闭合面内包含净电荷为Q.因场强只有x分量不为零,故只是二个垂直于x轴的平面上电场强度通量不为零.由高斯定理得:
-E1S1+ E2S2=Q / ε0 ( S1 = S2 =S )
则 Q = ε0S(E2- E1) = ε0Sb(x2- x1)
= ε0ba2(2a-a) =ε0ba3 = 8.85×10-12 C 4.(1025)
电荷面密度分别为+δ和-δ的两块“无限大”均匀带电平行平面,分别与x轴垂直相交于x1=a,x2=-a 两点.设坐标原点O处电势为零,试求空间的电势分布表示式并画出其曲线. 解:由高斯定理可得场强分布为:
E =-δ/ ε0? (-a<x<a)
E = 0 (-∞<x<-a ,a<x<+∞)
由此可求电势分布:在-∞<x≤-a区间 在-a≤x≤a区间 在a≤x<∞区间 5.(1179)如图所示,两个点电荷+q 和-3q,相距为d. 试求:
(1) 在它们的连线上电场强度的点与电荷为+q 的点电荷相距多远?
(2) 若选无穷远处电势为零,两点电荷之间电势U=0的点与电荷为+q的点电荷相距多远?解:设点电荷q所在处为坐标原点O,x轴沿两点电荷的连线 (1) 设的点的坐标为,则 另有一解不符合题意,舍去. (2) 设坐标x处U=0,则 得 d- 4x = 0, x = d/4 可得 解出 6.(0250)在强度的大小为E,方向竖直向上的匀强电场中,有一半径为R的半球形光滑绝缘槽放在光滑水平面上(如图所示).槽的质量为M,一质量为m带有电荷+q 的小球从槽的顶点A处由静止释放.如果忽略空气阻力且质点受到的重力大于其所受电场力,求: (1) 小球由顶点A滑至半球最低点B时相对地面的速度; (2) 小球通过B点时,槽相对地面的速度; (3) 小球通过B点后,能不能再上升到右端最高点C?解:设小球滑到B点时相对地的速度为v,槽相对地的速度为V.小球从A→B过程中球、槽组成的系统水平方向动量守恒, mv+MV=0 ① 对该系统,由动能定理 mgR-EqR=(mv2+MV2)/2 ② ①、②两式联立解出 方向水平向右 方向水平向左 小球通过B点后,可以到达C点 7.(1081)一均匀电场,场强大小为E=5×104 N/C,方向竖直朝上,把一电荷为q= 2.5×10-8 C的点电荷,置于此电场中的a点,如图所示.求此点电荷在下列过程中电场力作的功.
(1) 沿半圆路径Ⅰ移到右方同高度的b点, =45 cm;
(2) 沿直线路径Ⅱ向下移到c点, =80 cm;
(3) 沿曲线路径Ⅲ朝右斜上方向移到d点, =260 cm(与水平方向成45°角). 解:(1) (2) =-1×10-3 J (3) =2.3×10-3 J 8.(1276)
如图所示,三个“无限长”的同轴导体圆柱面A、B和C,半径分别为Ra、Rb、Rc.圆柱面B上带电荷,A和C都接地.求B的内表面上电荷线密度λ1和外表面上电荷线密度λ2之比值λ1/ λ2.解:设B上带正电荷,内表面上电荷线密度为λ1,外表面上电荷线密度为λ2,而A、C上相应地感应等量负电荷,如图所示.则A、B间场强分布为 E1=λ1 / 2πε0r,方向由B指向A B、C间场强分布为 E2=λ2 / 2πε0r,方向由B指向C B、A 间电势差 B、C 间电势差 因UBA=UBC ,得到 9.(1072)
在真空中一长为l=10 cm的细杆上均匀分布着电荷,其电荷线密度λ= 1.0×10-5 C/m.在杆的延长线上,距杆的一端距离d=10 cm的一点上,有一点电荷q0= 2.0×10-5 C,如图所示.试求该点电荷所受的电场力.(真空介电常量ε0=8.85×10-12 C2·N-1·m-2 )解:选杆的左端为坐标原点,x轴沿杆的方向 .在x处取一电荷元λdx,它在点电荷所在处产生场强为: 整个杆上电荷在该点的场强为: 点电荷q0所受的电场力为: =0.90 N 沿x轴负向 10.(1245)如图所示,有一高为h 的直角形光滑斜面, 斜面倾角为a.在直角顶点A处有一电荷为-q 的点电荷.另有一质量为m、电荷+q 的小球在斜面的顶点B 由静止下滑.设小球可看作质点,试求小球到达斜面底部C点时的速率. 解:因重力和电场力都是保守力,小球从顶点B 到达底部C点过程中能量守恒. ∴ 理论推导与证明1.(1265)真空中点电荷q的静电场场强大小为
式中r 为场点离点电荷的距离.当r→0时,E→∞,这一推论显然是没有物理意义的,应如何解释? 答:点电荷的场强公式仅适用于点电荷,当r→0时,任何带电体都不能视为点
电荷,所以点电荷场强公式已不适用.
若仍用此式求场强E,其结论必然是错误的.当r→0时,需要具体考虑带
电体的大小和电荷分布,这样求得的E就有确定值. 2.(1295)电荷为q1的一个点电荷处在一高斯球面的中心处,问在下列三种情况下,穿过此高斯面的电场强度通量是否会改变?电场强度通量各是多少?
(1) 将电荷为q2的第二个点电荷放在高斯面外的附近处;
(2) 将上述的q2放在高斯面内的任意处;
(3) 将原来的点电荷移离高斯面的球心,但仍在高斯面内答:根据高斯定理,穿过高斯面的电通量仅取决于面内电量的代数和,而与面内电荷的分布情况及面外电荷无关,故:
(1) 电通量不变, ?1=q1 / ε0;
(2) 电通量改变,由?1变为?2=(q1+q2 ) / ε0;
(3) 电通量不变,仍为?1. 静电场中电介质选择题1.(1137)有一接地的金属球,用一弹簧吊起,金属球原来不带电.若在它的下方放置一电荷为q 的点电荷,如图所示,则
(A) 只有当q > 0 时,金属球才下移.
(B) 只有当q < 0 时,金属球才下移.
(C) 无论q 是正是负金属球都下移.
(D) 无论q 是正是负金属球都不动. [ ]C 2.(1101)一导体球外充满相对介电常量为εr 的均匀电介质,若测得导体表面附近场强为E,则导体球面上的自由电荷面密度δ为
(A) ε 0 E. (B) ε 0 εr E.
(C) ε r E. (D) (ε 0 εr - ε 0)E. [ ] B 3.(1139)
一个大平行板电容器水平放置,两极板间的一半空间充有各向同性均匀电介质,另一半为空气,如图.当两极板带上恒定的等量异号电荷时,有一个质量为m、带电荷为+q 的质点,在极板间的空气区域中处于平衡.此后,若把电介质抽去 ,则该质点
(A) 保持不动. (B) 向上运动.
(C) 向下运动. (D) 是否运动不能确定. [ ] B 4.(1224)
一空气平行板电容器充电后与电源 断开,然后在两极板间充满某种各向同性、均匀电介质,则电场强度的大小E、电容C、电压U、电场能量W四个量各自与充入介质前相比较,增大(↑)或减小(↓)的情形为
(A) E↑,C↑,U↑,W↑.
(B) E↓,C↑,U↓,W↓.
(C) E↓,C↑,U↑,W↓.
(D) E↑,C↓,U↓,W↑. [ ] B 填空题1.(1152)
如图所示,把一块原来不带电的金属板B,移近一块已带有正电荷Q的金属板A,平行放置.设两板面积都是S,板间距离是d,忽略边缘效应.当B板不接地时,两板间
势差UAB =___________________ ;B 板接地时两板间电势差
__________ . 2.(1116)一空气平行板电容器,两极板间距为d,充电后板间电压为U.然后将电源断开,在两板间平行地插入一厚度为d/3的金属板,则板间电压变成
U' =________________ .2U/3 3.(1320)
一平行板电容器,两板间充满各向同性均匀电介质,已知相对介电常量为
εr .若极板上的自由电荷面密度为δ ,则介质中电位移的大小D
=____________,
电场强度的大小E =____________________. δ δ / ( ε 0ε r ) 4.(1237)
两个电容器1和2,串联以后接上电动势恒定的电源充电.在电源保持联接
的情况下,若把电介质充入电容器2中,则电容器1上的电势差______________;
电容器1极板上的电荷____________.(填增大、减小、不变) 增大 增大 5.(5107)
1、2是两个完全相同的空气电容器.将其充电后与电源断开,再将一块各向同性均匀电介质板插入电容器1的两极板间,如图所示, 则电容器2 的电压U2,电场能量W2如何变
化?(填增大,减小或不变) U2 _________,
W2 _____________. 减小 减小 计算题1.(5425)半径分别为R1和R2 (R2 > R1 )的两个同心导体薄球壳,分别带有电荷Q1和Q2,今将内球壳用细导线与远处半径为r 的导体球相联,如图所示, 导体球原来不带电,试求相联后导体球所带电荷q. 解:设导体球带电q,取无穷远处为电势零点,则
导体球电势: 内球壳电势: 二者等电势,即 解得 2.(1182)
一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半径分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量为εr 的各向同性、均匀电介质.电容器接在电压U = 32 V的电源上,(如图所示),试求距离轴线R = 3.5 cm处的A点的电场强度和A点与外筒间的电势差. 解:设内外圆筒沿轴向单位长度上分别带有电荷+? 和?? , 根据高斯定理可求得两圆筒间任一点的电场强度为 则两圆筒的电势差为 解得 于是可求得A点的电场强度为 = 998 V/m 方向沿径向向外 A点与外筒间的电势差: = 12.5 V 3.(5682)
一绝缘金属物体,在真空中充电达某一电势值,其电场总能量为W0.若断开电源,使其上所带电荷保持不变,并把它浸没在相对介电常量为εr 的无限大的各向同性均匀液态电介质中,问这时电场总能量有多大?解:因为所带电荷保持不变,故电场中各点的电位移矢量 保持不变, 又 因为介质均匀,∴电场总能量 4.(1489)半径分别为 1.0 cm与 2.0 cm 的两个球形导体,各带电荷 1.0×10-8 C,两球相 距很远.若用细导线将两球相连接.求(1) 每个球所带电荷;(2) 每球的电
势.( )解:两球相 距很远,可视为孤立导体,互不影响.球上电荷均匀分布.设两球半径分别为r1和r2,导线连接后的电荷分别为q1和q2,而q1 + q2 = 2q,则两球电势分别是 两球相连后电势相等, ,则有 由此得到 C C 两球电势 V 改错1.(1165)
同一种材料的导体A1、A2紧靠一起, 放在外电场中(图a).将A1、A2 分开后撤去电场(图b).下列说法是否正确? 如有错误请改正.
(1) 在图(a)中,A1 左端的电势比A2右端的电势低.
(2) 在图(b)中,A1 的电势比A2 的电势低 答:(1) 在图(a)中,A1 左端和A2 右端电势相等
(2) 正确. 2.(5117)
两块平行放置的无限大导体平板A 和B,面积均为S.A板带电荷为+Q (>0),B 板不带电.有人画出导体静电平衡时两板上的电荷分布如图所示.所画电荷分布是否正确如有错误,请指出,并画出正确的电荷分布图. 答:所画电荷分布不能使A、B两板内部场强为零,所以是错误的.
正确的电荷分布如右图所示. 问答题1.(1166)
有两个相距“无限远”的金属球,其中一个带正电荷Q,它在球外离球心为r 处的
一点电场强度为 ,另一金属球带负电荷Q2,它在球外离球心为r 的一点处
场强为 .当两球从“无限远”移近到两球心相 距为2 r 时,在球心连线中点
处的合场强为 ,你认为这一结果对吗?为什么? 答:结论是不对的!
当两金属球相距“无限远”时,两球上电荷是均匀分布的,在这样的情形下,所得
的场强为 和 .当两球靠近时,由于静电感应,两球上电荷不再均匀
分布.因而在两球连线中点处的场强已不再分别是 和 ,因而合场
强 了.
