9.1.2不等式的性质

课件20张PPT。9-1-2 不等式的性质1、观察下面这几个式子，完成下面的填空。回忆思考∵∴同一个数同一个整式等式的基本性质1：,,.2、继续观察下面这几个式子，完成下面的填空。回忆思考∵∴同一个数等式的基本性质2：那么不等式有没有类似的性质呢？,,.情境 有甲、乙两同学，甲的钱多于乙的钱，然后再给甲、乙两人相同的钱，则甲、乙两人的钱谁多谁少？
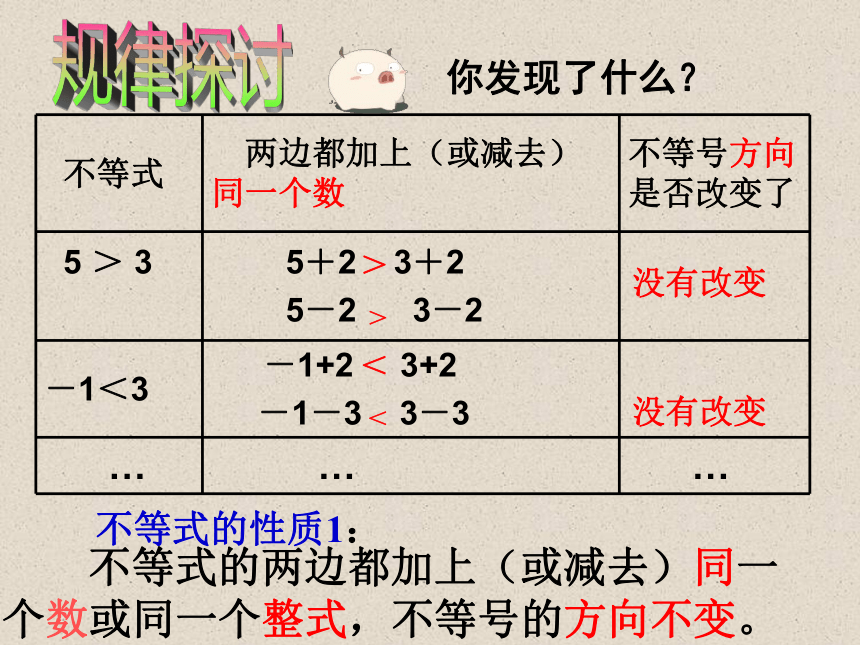
如果他们都捐出同样的钱，情况又会如何？ 规律探讨 不等式的性质1： 不等式的两边都加上（或减去）同一个数或同一个整式，不等号的方向不变。没有改变没有改变你发现了什么？＞＜＞＜ 如果a>b ，
那么 a+c>b+c(或a-c>b-c)不等式的性质1 将不等式6＞2的两边都乘以同一个不为0的数，比较所得结果。 用“＜”或“＞”填空： 6×1（ ）2×1，
6×2（ ）2×2，
6×3（ ）2×3，
6×4（ ）2×4，
…＞＞＞＞你有什么发现？6×（-1）（ ）2×（-1），
6×（-2）（ ）2×（-2），
6×（-3）（ ）2×（-3），
6×（-4）（ ）2×（-4），
…＜＜＜＜你又有什么发现？不等式的两边都乘以（或除以）同一个正数，不等号的方向不变；如果a>b，c<0 ，那么acb，c>0 ，那么ac>bc,不等式的性质2不等式的性质3 不等式的两边都乘以0，会出现什么样的结果？
思考：应用举例例1：将下列不等式化成“x＞a”或“x＜a”的形式： （1）x－5＞－1;
（2）－2x＞3;
（3）3x＜－9. 解： (1)根据不等式的性质1，两边都加上5，得
x＞－1+5
即x＞4;应用举例例1：将下列不等式化成“x＞a”或“x＜a”的形式： （1）x－5＞－1;
（2）－2x＞3;
（3）3x＜－9. 解： (2)根据不等式的性质3，两边都除以－2，得
x＜－ ; 应用举例例1：将下列不等式化成“x＞a”或“x＜a”的形式： （1）x－5＞－1;
（2）－2x＞3;
（3）3x＜－9. 解： (3)根据不等式的性质2，两边都除以3，得
x＜－3. 例2 用“>”或“<”填空：
(1)a＋3_____b＋3；(ab)；
(3) (a>b)；
(4)a－4_____b－4 (a－b>0) ；
(5)若a>0，b>0，则ab_____0；
(6)若b<0，则a＋b______a；
(7)当a<0时，b_____0时，ab>0． ＜＜＜＜＞＞＞
不等式的性质与等式的性质有什么相同点、不同点？ 1、如果x＋5＞4，那么两边都 可得 x ＞－1
2、在－7＜8 的两边都加上9可得 。
3、在5＞－2 的两边都减去6可得 。
4、在－3＞－4 的两边都乘以7可得 。
5、在－8＜0 的两边都除以8 可得 。 减去52＜17－1＞－8－21 ＞－ 28－1＜06、在不等式－8＜0的两边都除以－8可得 。
7、在不等式－3 x＜3的两边都除以－3可得 。
8、在不等式－3＞－4的两边都乘以－3可得 。
9、在不等式 的两边都乘以－1可得 。1＞09＜12＞＞＞＜1231说一说收获和体会 不等式的基本性质是什么?
和等式的基本性质相比，有什么相同和不同之处?
本节课你还有什么收获? 作业课本第128页练习第1、2、3题