复数的概念及其几何意义
图片预览



文档简介
课件19张PPT。bqr6401@126.com3.1数系的扩充和复数的概念bqr6401@126.com数系的扩充自然数有理数整数实数?bqr6401@126.com3.1 复数的概念知识回顾解一元二次方程 。对于实系数一元二次方程 ,
,方程没有实数根.我们能否将实数集进行扩充,使得在新的数集中,该问题能得到圆满解决呢? bqr6401@126.com引入一个新数 , 叫做虚数单位,并规定: 虚数单位(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立. bqr6401@126.com形如 的数,叫做复数
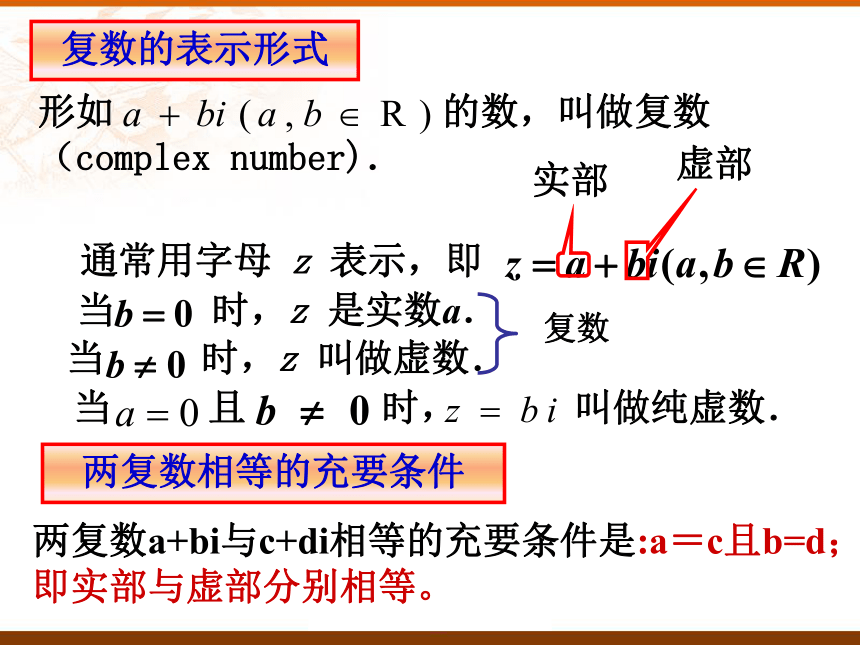
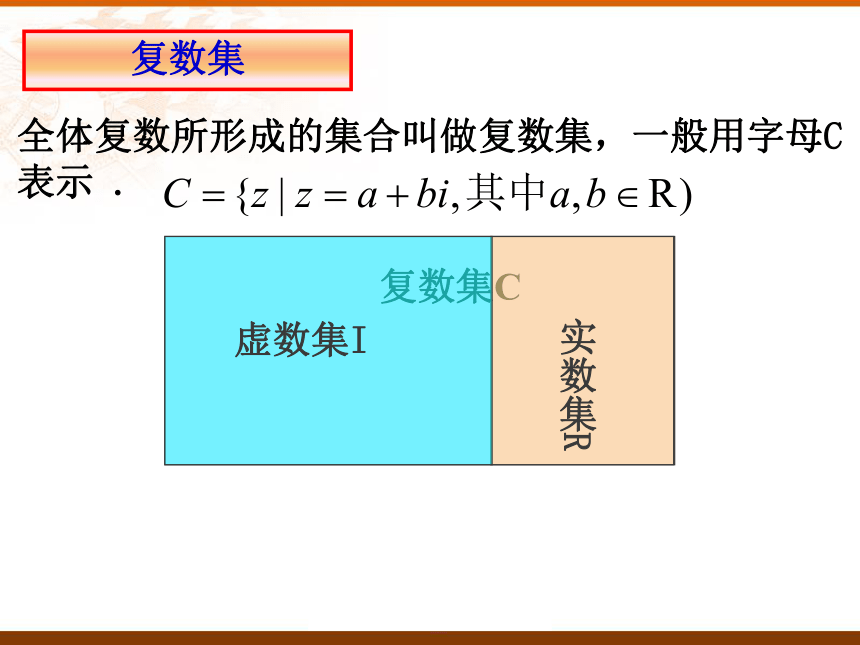
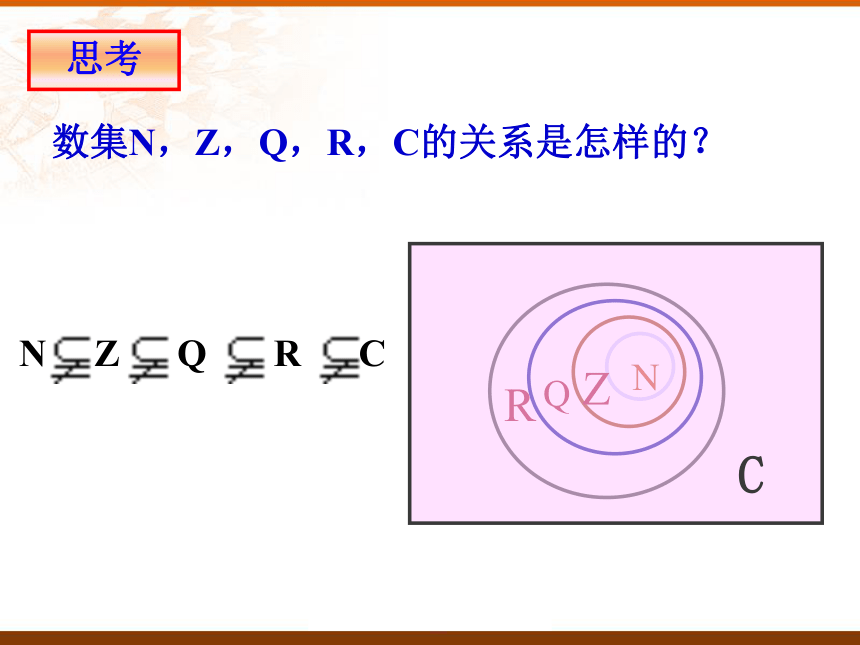
(complex number). 复数的表示形式通常用字母 z 表示,即当 时,z 是实数a.当 时,z 叫做虚数.当 且 时, 叫做纯虚数.两复数a+bi与c+di相等的充要条件是:a=c且b=d;即实部与虚部分别相等。两复数相等的充要条件bqr6401@126.com全体复数所形成的集合叫做复数集,一般用字母C表示 .复数集bqr6401@126.comN Z Q R C思考数集N,Z,Q,R,C的关系是怎样的?bqr6401@126.com例1:实数m取什么值时,复数 是
(1)实数? (2)虚数? (3)纯虚数?解:(1)当 ,即 时,复数z是实数.(2)当 ,即 时,复数z是虚数.(3)当 ,且 ,即 时,复数z 是纯虚数.新授课bqr6401@126.com新授课例2 已知 ,其中 ,求解:由复数相等的定义,得方程组解得练习课本练习P104 1、2、3bqr6401@126.com复数的几何意义如图,点Z的横坐标是a,纵坐标是b,复数z=a+bi可用Z(a,b)表示。这个建立了直角坐标系来表示复数的平面叫做复平面引入点其中:x轴叫实轴,y轴叫做虚轴,实轴上的点都表示实数; 除了原点y,虚轴上的点都表示纯虚数。象限中的点都表示非纯虚数。bqr6401@126.com新授课复数z=a+bi?复平面内的点Z(a,b)?平面向量平面向量bqr6401@126.com新授课例3:实数m取什么值时,复数
对应的点
(1)位于第一、三象限?
(2)位于第四象限?bqr6401@126.com练习:P105 1、2、3bqr6401@126.com 自然数概念可溯源于原始人类用匹配方法计数。古希腊人用小石卵记畜群的头数或部落的人数 。 英文calculate(计算)一词是从希腊文calculus (石卵)演变来的。中国古藉《易.系辞》中说:「上古结绳而治,后世圣人易之以书契。」
直至1889年,皮亚诺才建立自然数序数理论。 自然数返回bqr6401@126.com 零不仅表示「无」,更是表示空位的符号。中国古代用算筹计算数并进行运算时,空位不放算筹,虽无空 位记号,但仍能为位值记数与四则运算创造良好的条件。印度-阿拉伯命数法中的零(zero)来自印度的(sunya )字,其原意也是「空」或「空白」。 中国最早引进了负数。《九章算术.方程》中论述的「正负数」,就是整数的加减法。减法的需要也促进 了负整数的引入。减法运算可看作求解方程a+x=b,如果a,b是自然数,则所给方程未必有自然数解。为了使它恒有解,就有必要把自然数系扩大为整数系。 整数返回bqr6401@126.com分 数 原始的分数概念来源于对量的分割。如《说文·八部》对“分”的解释:“分,别也。从八从刀,刀以分别物也。”但是,《九章算术》中的分数是从除法运算引入的。其“合分术”有云:“实如法而一。不满法者,以法命之。”这句话的今译是:被除数除以除数。如果不能除尽,便定义了一个分数。
古埃及人约于公元前17世纪已使用分数。 返回bqr6401@126.com 为表示各种几何量(例如长度、面积、体积)与物理量(例如速率、力的大小),人类很早已发现有必要 引进无理数。约在公元前530,毕达哥拉斯学派已知道边长为1的正方形的对角线的长度(即 )不能是有理数。
15世纪达芬奇(Leonardo da Vinci, 1452- 1519) 把它们称为是“无理的数”(irrational number),开普勒(J. Kepler, 1571- 1630)称它们是“不可名状”的数。
法国数学家柯西(A.Cauchy,1789- 1875)给出了回答:无理数是有理数序列的极限。
由于有理数可表示成有限小数或无限循环小数,人们想到用“无限不循环小数”来定义无理数,这也是直至19世纪中叶以前的实际做法。 无理数返回bqr6401@126.com 实数系的逻辑基础直到19世纪70年代才得以奠定。从19世纪20年代肇始的数学分析严密化潮流,使得数学 家们认识到必须建立严格的实数理论,尤其是关于实数系的连续性的理论。在这方面,外尔斯特拉斯(1859年 开始)、梅雷(1869)、戴德金(1872)与康托尔(1872 )作出了杰出的贡献。 实数返回bqr6401@126.com复数 从16世纪开始,解高于一次的方程的需要导致复数概念的形式。用配方法解一元二次方程就会遇到负数开平方的问题。卡尔达诺在《大法》(1545)中阐述一元三次方程解法时,发现难以避免复数。关于复数及其代 数运算的几何表示,是18世纪末到19世纪30年代由韦塞尔、阿尔根和高斯等人建立的。 哈密顿认真地研究了从实数扩张到复数的过程。他于1843年提出了「四元数」的概念,其后不久,凯莱又 用四元数的有序对定义了八元数。它们都被称为「超复数」,如果舍弃更多的运算性质,超复数还可扩张到十六元数、三十二元数等等。 返回
,方程没有实数根.我们能否将实数集进行扩充,使得在新的数集中,该问题能得到圆满解决呢? bqr6401@126.com引入一个新数 , 叫做虚数单位,并规定: 虚数单位(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立. bqr6401@126.com形如 的数,叫做复数
(complex number). 复数的表示形式通常用字母 z 表示,即当 时,z 是实数a.当 时,z 叫做虚数.当 且 时, 叫做纯虚数.两复数a+bi与c+di相等的充要条件是:a=c且b=d;即实部与虚部分别相等。两复数相等的充要条件bqr6401@126.com全体复数所形成的集合叫做复数集,一般用字母C表示 .复数集bqr6401@126.comN Z Q R C思考数集N,Z,Q,R,C的关系是怎样的?bqr6401@126.com例1:实数m取什么值时,复数 是
(1)实数? (2)虚数? (3)纯虚数?解:(1)当 ,即 时,复数z是实数.(2)当 ,即 时,复数z是虚数.(3)当 ,且 ,即 时,复数z 是纯虚数.新授课bqr6401@126.com新授课例2 已知 ,其中 ,求解:由复数相等的定义,得方程组解得练习课本练习P104 1、2、3bqr6401@126.com复数的几何意义如图,点Z的横坐标是a,纵坐标是b,复数z=a+bi可用Z(a,b)表示。这个建立了直角坐标系来表示复数的平面叫做复平面引入点其中:x轴叫实轴,y轴叫做虚轴,实轴上的点都表示实数; 除了原点y,虚轴上的点都表示纯虚数。象限中的点都表示非纯虚数。bqr6401@126.com新授课复数z=a+bi?复平面内的点Z(a,b)?平面向量平面向量bqr6401@126.com新授课例3:实数m取什么值时,复数
对应的点
(1)位于第一、三象限?
(2)位于第四象限?bqr6401@126.com练习:P105 1、2、3bqr6401@126.com 自然数概念可溯源于原始人类用匹配方法计数。古希腊人用小石卵记畜群的头数或部落的人数 。 英文calculate(计算)一词是从希腊文calculus (石卵)演变来的。中国古藉《易.系辞》中说:「上古结绳而治,后世圣人易之以书契。」
直至1889年,皮亚诺才建立自然数序数理论。 自然数返回bqr6401@126.com 零不仅表示「无」,更是表示空位的符号。中国古代用算筹计算数并进行运算时,空位不放算筹,虽无空 位记号,但仍能为位值记数与四则运算创造良好的条件。印度-阿拉伯命数法中的零(zero)来自印度的(sunya )字,其原意也是「空」或「空白」。 中国最早引进了负数。《九章算术.方程》中论述的「正负数」,就是整数的加减法。减法的需要也促进 了负整数的引入。减法运算可看作求解方程a+x=b,如果a,b是自然数,则所给方程未必有自然数解。为了使它恒有解,就有必要把自然数系扩大为整数系。 整数返回bqr6401@126.com分 数 原始的分数概念来源于对量的分割。如《说文·八部》对“分”的解释:“分,别也。从八从刀,刀以分别物也。”但是,《九章算术》中的分数是从除法运算引入的。其“合分术”有云:“实如法而一。不满法者,以法命之。”这句话的今译是:被除数除以除数。如果不能除尽,便定义了一个分数。
古埃及人约于公元前17世纪已使用分数。 返回bqr6401@126.com 为表示各种几何量(例如长度、面积、体积)与物理量(例如速率、力的大小),人类很早已发现有必要 引进无理数。约在公元前530,毕达哥拉斯学派已知道边长为1的正方形的对角线的长度(即 )不能是有理数。
15世纪达芬奇(Leonardo da Vinci, 1452- 1519) 把它们称为是“无理的数”(irrational number),开普勒(J. Kepler, 1571- 1630)称它们是“不可名状”的数。
法国数学家柯西(A.Cauchy,1789- 1875)给出了回答:无理数是有理数序列的极限。
由于有理数可表示成有限小数或无限循环小数,人们想到用“无限不循环小数”来定义无理数,这也是直至19世纪中叶以前的实际做法。 无理数返回bqr6401@126.com 实数系的逻辑基础直到19世纪70年代才得以奠定。从19世纪20年代肇始的数学分析严密化潮流,使得数学 家们认识到必须建立严格的实数理论,尤其是关于实数系的连续性的理论。在这方面,外尔斯特拉斯(1859年 开始)、梅雷(1869)、戴德金(1872)与康托尔(1872 )作出了杰出的贡献。 实数返回bqr6401@126.com复数 从16世纪开始,解高于一次的方程的需要导致复数概念的形式。用配方法解一元二次方程就会遇到负数开平方的问题。卡尔达诺在《大法》(1545)中阐述一元三次方程解法时,发现难以避免复数。关于复数及其代 数运算的几何表示,是18世纪末到19世纪30年代由韦塞尔、阿尔根和高斯等人建立的。 哈密顿认真地研究了从实数扩张到复数的过程。他于1843年提出了「四元数」的概念,其后不久,凯莱又 用四元数的有序对定义了八元数。它们都被称为「超复数」,如果舍弃更多的运算性质,超复数还可扩张到十六元数、三十二元数等等。 返回
