4.3.3 余角和补角课件

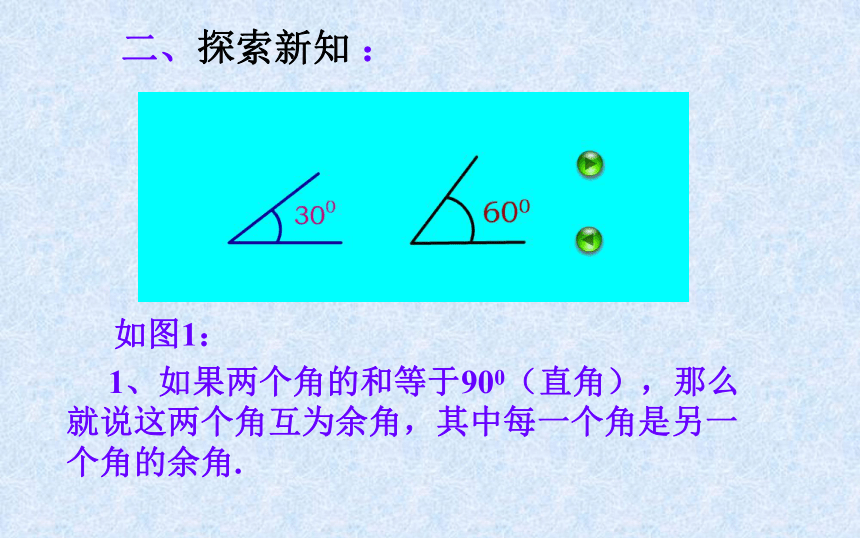
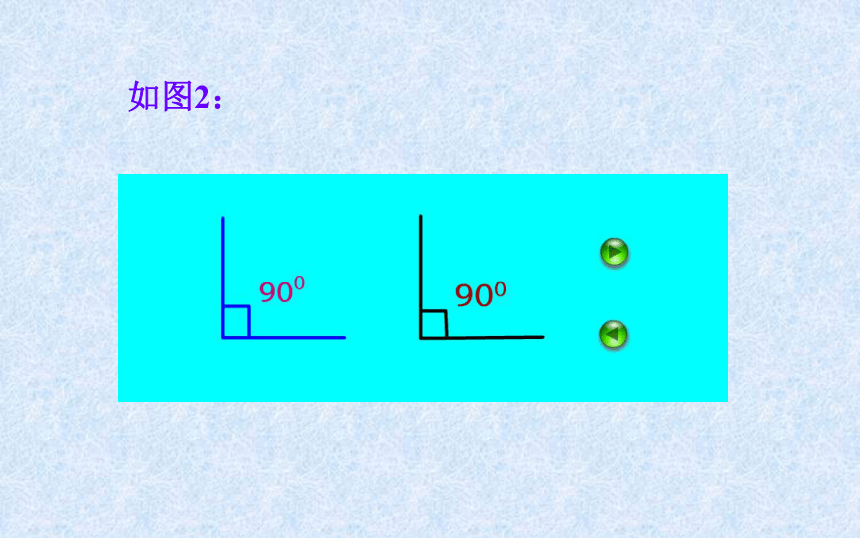
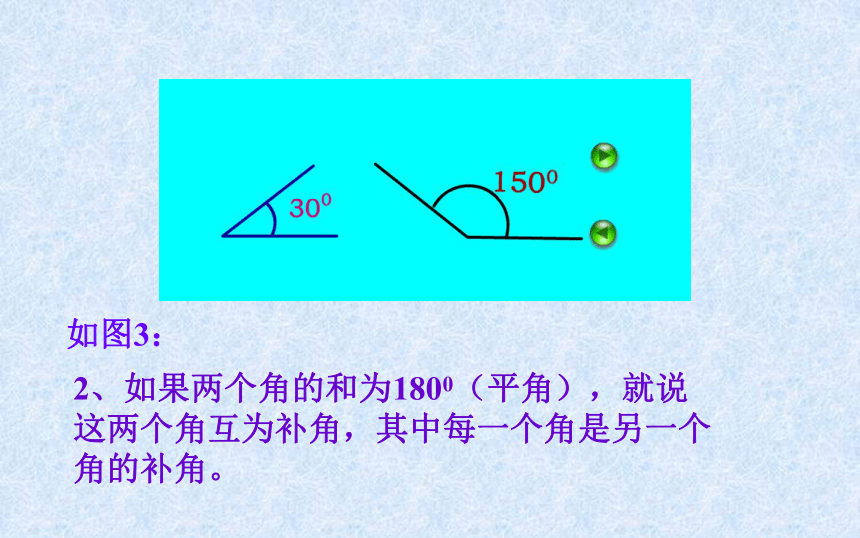
课件14张PPT。余角与补角一、引入新课 ：900900900180018001800二、探索新知 ： 1、如果两个角的和等于900（直角），那么就说这两个角互为余角，其中每一个角是另一个角的余角.如图1：如图2：2、如果两个角的和为1800（平角），就说这两个角互为补角，其中每一个角是另一个角的补角。如图3：例1、①若∠A+27°=90°∠B+27°=90°
则∠A与∠B的关系 理由：∵∠A+27°=90° ∠B+27°=90°∴∠A=90°－27°=63°∠B=90°－27°=63°∴∠A=∠B相等②若∠1+∠2=90° ∠3+∠4=90°
且∠1=∠3 则∠2与∠4的关系 相等理由：∵∠1+∠2=90°∴∠2=90°－∠1 又∵∠1=∠3∴∠2=∠4∠3+∠4=90°∠4=90°－∠3结论：同角（或等角）的余角相等三、例题例1 ③、若∠5+100°=180° ∠6+100°=180°
则∠5与∠6的关系是 相等理由：∵∠5+100°=180°∠6+100°=180°∴∠5=∠6④若∠7+∠8=180° ∠9+∠10=180°，
且∠8=∠10，则∠7与∠9的关系 相等理由：∵∠7+∠8=180° ∠9+∠10=180°∴∠7=1800－∠8∠9=180°－∠10又∵∠8=∠10∴∠7=∠9结论：同角（或等角）的补角相等三、例题课堂练习1:(1).420角与480角互为余角 ( )
(2).280角与720角互为余角 ( )
(3).∠3+ ∠4=900,则∠3是∠4的余角 . ( )
(4).∠5+ ∠6+ ∠7=900,则∠5、 ∠6、 ∠7
互为余角 ( )
(5).两个锐角一定互为余角. ( )课堂练习2:
(1).310角的余角是( )角;
(2).12012 ′角 是( 　 )的余角；
(3).某个角的余角为63036 ′,则这个角为( 　 )；
(4).如果一个角比它的余角的2倍多300，
则这个角是（ ），它的余角是（ ）。 59077048 ′26024 ′700200解：设这个角为x0，则x=2（90—x）+30x=180—2x+303x=210x=70课堂练习3:
（1）两个直角互为补角。 （ ）
（2）72°角的补角是128°。 （ ）
（3）若∠A+∠B=180°，则∠A与∠B互为补角。 （ ）
（4）一个锐角与一个钝角一定互为补角. （ ）课堂练习4:
（1）59°31′角是 角的补角。
（2）一个角的余角是42°，则这个角的
补角是 。
（3）一个角的补角比它的3倍少60°，
则这个角为 。120°29′132°60°解：设这个角为x°，则180－x=3x－60°－4x=－240x=60理由：∵ △ ABC的内角和为180° ∠ACB=90°∴∠A+∠B=180°－90°=90°∴∠A是∠B的余角同理∠DCB是∠B的余角∴∠A=∠DCB （同角的余角相等）同理：∠B=∠ACD答：有相等的角，分别是∠A=∠DCB， ∠B=∠ACD， ∠ACB= ∠ADC =∠CDB1、两角互为余角，互为补角的概念.六、小结：2、互为余角、互为补角的性质.3、会用互为余角、互为补角的性质，进行角的有关计算.谢谢!