【青岛版】八年级数学上册课件 1.2怎样判定三角形全等(第2课时)
文档属性
| 名称 | 【青岛版】八年级数学上册课件 1.2怎样判定三角形全等(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 97.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 00:00:00 | ||
图片预览





文档简介
课件16张PPT。1.2 怎样判定三角形全等(2)教学目标1.知道三角形全等“角边角”,“角角边”的内容;
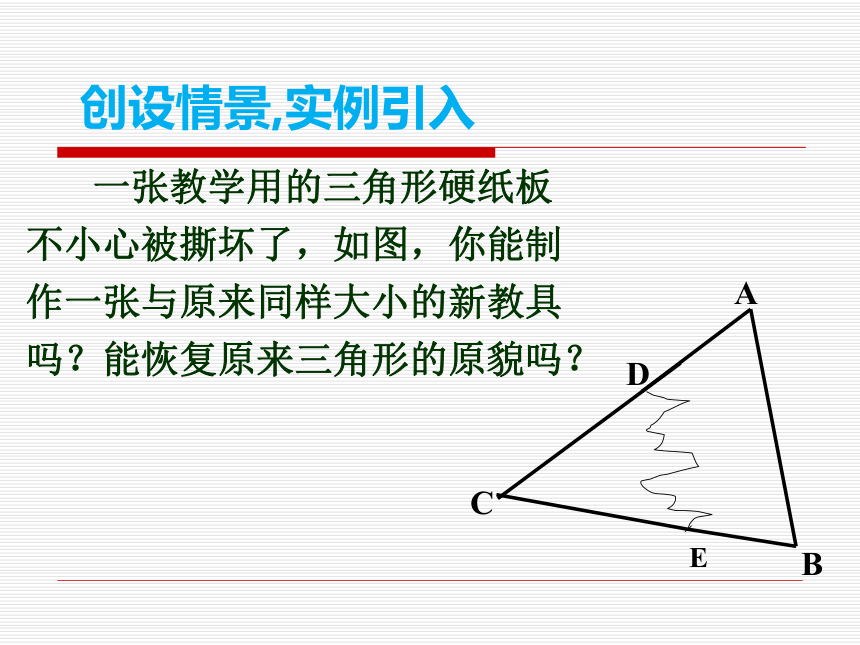
2.会运用“ASA”、“AAS”识别三角形全等,为证明线段相等或角相等创造条件.1.什么是全等三角形? 2. 我们已学了那些判定三角形全等的方法? 复习回顾 ?边角边(SAS): 有两边和它们夹角对应相等的两个三角形全等。?定义 一张教学用的三角形硬纸板
不小心被撕坏了,如图,你能制
作一张与原来同样大小的新教具
吗?能恢复原来三角形的原貌吗?创设情景,实例引入C 如果两个三角形具备两角一边对应相等,有几种可能情况?1、两角夹边对应相等。共三种情况2、有两个角和其中一个角的对边对应相等3、有两个角对应相等,以及一个三角形中的夹边与另一个三角形中一对应角的对边对应相等。探究新知 探究1:我们先来探究两角夹边对应相等时 两个三角形是否全等 1、如图:在△ABC与△A′B′C′中,BC=B′C′,∠B=∠B′,添加条件∠C=∠C′
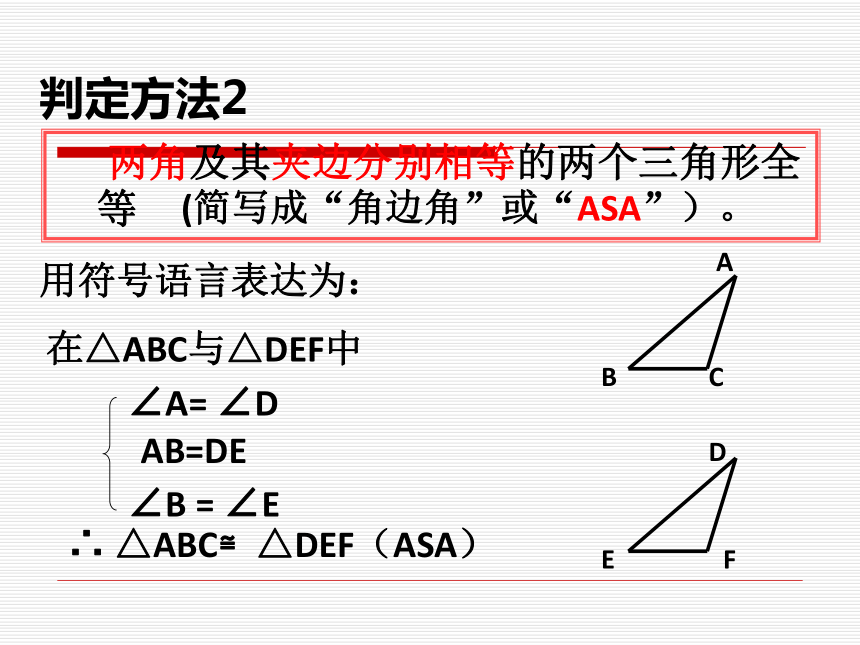
△ABC与△A′B′C′全等吗?C′3、你能得出什么结论?说明理由。判定方法2 两角及其夹边分别相等的两个三角形全等用符号语言表达为:在△ABC与△DEF中∴ △ABC≌△DEF(ASA)∠A= ∠D∠B = ∠EAB=DE(简写成“角边角”或“ASA”)。情景验证:你能说明这样做的道理吗?C例题讲解:例3已知∠ACB=∠DFE,
∠B=∠E,BC=EF,那么△ABC与△DEF全等吗?为什么? 如图,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
如图: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?
能利用角边角条件说明你的结论吗?理由:因为 ∠A+∠B+∠C=180o
∠D+∠E+∠F=180o所以 ∠C=∠F又因为 ∠A=∠D, ∠B=∠E 在△ABC和△DEF中所以 △ABC≌△DEF (ASA) 有两个角和其中一个角的对边对应相等
的两个三角形是否全等?根据ASA, 两角分别相等且其中一组等角的对边也相等的两个三角形全等。 判定方法3用符号语言表达为:在△ABC和△DEF中∴ △ABC≌△DEF (AAS)(简写“角角边”或“AAS”)例4在△ABD 与△CDB中,已知∠A=∠C,再添加一个什么条件,就可以判定△ABD 与△CDB全等?说明理由AO=BO还有吗?填一填AC=BD或CO=DO 有两个角对应相等,以及一个三角形中两个对应角的夹边与另一个三角形中一对应角的对边对应相等的两个三角形是否全等呢?观
察如图:△ABC是直角三角形,
∠ACB=90o ,CD AB,垂足为D。则在△ACD与△CBD中便有:∠A= ∠1
∠ADC= ∠CDB=90o
CD=CD试想△ACD与△CBD会全等吗? 两个三角形并非有两角一边对应相等便能判别它们全等,只有满足(ASA)和(AAS)才行。1.你能总结出我们学过哪些判定三角形
全等的方法吗?2.要根据题意选择适当的方法。3.要线段或角相等,就是想法判定它们所
在的两个三角形全等。
2.会运用“ASA”、“AAS”识别三角形全等,为证明线段相等或角相等创造条件.1.什么是全等三角形? 2. 我们已学了那些判定三角形全等的方法? 复习回顾 ?边角边(SAS): 有两边和它们夹角对应相等的两个三角形全等。?定义 一张教学用的三角形硬纸板
不小心被撕坏了,如图,你能制
作一张与原来同样大小的新教具
吗?能恢复原来三角形的原貌吗?创设情景,实例引入C 如果两个三角形具备两角一边对应相等,有几种可能情况?1、两角夹边对应相等。共三种情况2、有两个角和其中一个角的对边对应相等3、有两个角对应相等,以及一个三角形中的夹边与另一个三角形中一对应角的对边对应相等。探究新知 探究1:我们先来探究两角夹边对应相等时 两个三角形是否全等 1、如图:在△ABC与△A′B′C′中,BC=B′C′,∠B=∠B′,添加条件∠C=∠C′
△ABC与△A′B′C′全等吗?C′3、你能得出什么结论?说明理由。判定方法2 两角及其夹边分别相等的两个三角形全等用符号语言表达为:在△ABC与△DEF中∴ △ABC≌△DEF(ASA)∠A= ∠D∠B = ∠EAB=DE(简写成“角边角”或“ASA”)。情景验证:你能说明这样做的道理吗?C例题讲解:例3已知∠ACB=∠DFE,
∠B=∠E,BC=EF,那么△ABC与△DEF全等吗?为什么? 如图,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
如图: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?
能利用角边角条件说明你的结论吗?理由:因为 ∠A+∠B+∠C=180o
∠D+∠E+∠F=180o所以 ∠C=∠F又因为 ∠A=∠D, ∠B=∠E 在△ABC和△DEF中所以 △ABC≌△DEF (ASA) 有两个角和其中一个角的对边对应相等
的两个三角形是否全等?根据ASA, 两角分别相等且其中一组等角的对边也相等的两个三角形全等。 判定方法3用符号语言表达为:在△ABC和△DEF中∴ △ABC≌△DEF (AAS)(简写“角角边”或“AAS”)例4在△ABD 与△CDB中,已知∠A=∠C,再添加一个什么条件,就可以判定△ABD 与△CDB全等?说明理由AO=BO还有吗?填一填AC=BD或CO=DO 有两个角对应相等,以及一个三角形中两个对应角的夹边与另一个三角形中一对应角的对边对应相等的两个三角形是否全等呢?观
察如图:△ABC是直角三角形,
∠ACB=90o ,CD AB,垂足为D。则在△ACD与△CBD中便有:∠A= ∠1
∠ADC= ∠CDB=90o
CD=CD试想△ACD与△CBD会全等吗? 两个三角形并非有两角一边对应相等便能判别它们全等,只有满足(ASA)和(AAS)才行。1.你能总结出我们学过哪些判定三角形
全等的方法吗?2.要根据题意选择适当的方法。3.要线段或角相等,就是想法判定它们所
在的两个三角形全等。
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
