【青岛版】八年级数学上册课件 1.2怎样判定三角形全等(第3课时)
文档属性
| 名称 | 【青岛版】八年级数学上册课件 1.2怎样判定三角形全等(第3课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 00:00:00 | ||
图片预览


文档简介
课件14张PPT。1.2 怎样判定三角形全等(3)教学目标1.知道“边边边”的内容,会运用“SSS”识别三角形全等,为证明线段相等或角相等创造条件;
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
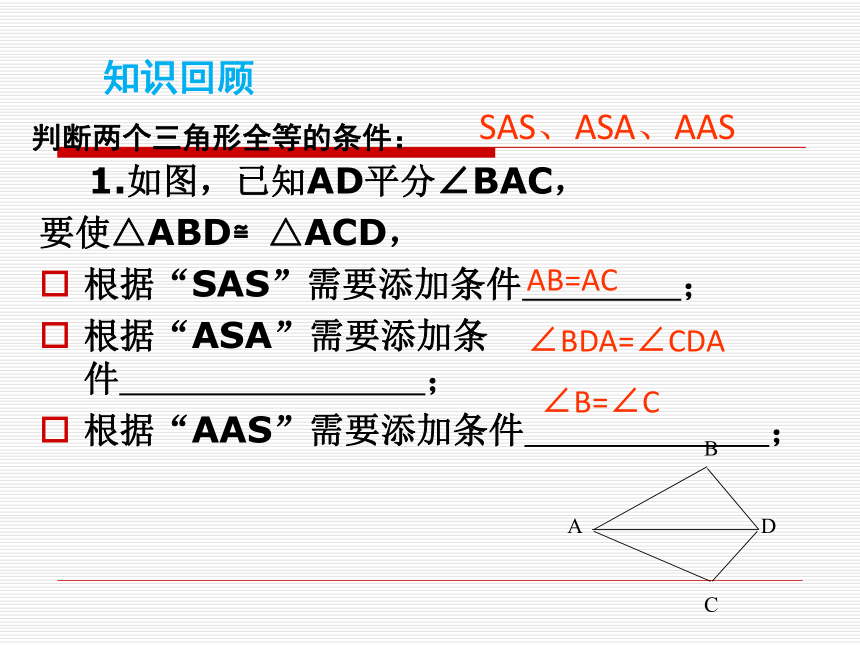
3.知道三角形的稳定性和四边形的不稳定性。 1.如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
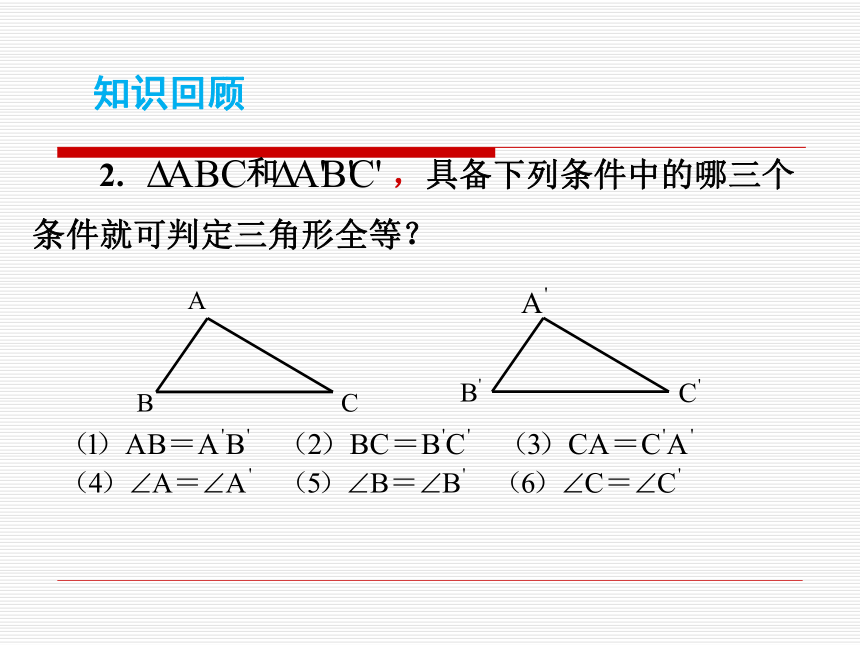
根据“AAS”需要添加条件 ;判断两个三角形全等的条件:AB=AC∠BDA=∠CDA∠B=∠CSAS、ASA、AAS知识回顾 2. ,具备下列条件中的哪三个
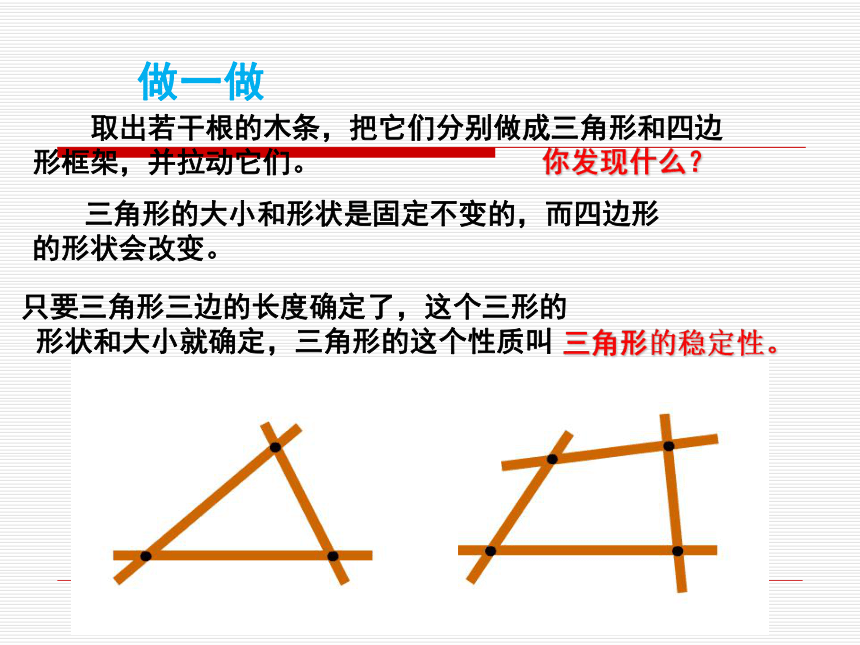
条件就可判定三角形全等?和知识回顾 取出若干根的木条,把它们分别做成三角形和四边形框架,并拉动它们。你发现什么? 三角形的大小和形状是固定不变的,而四边形
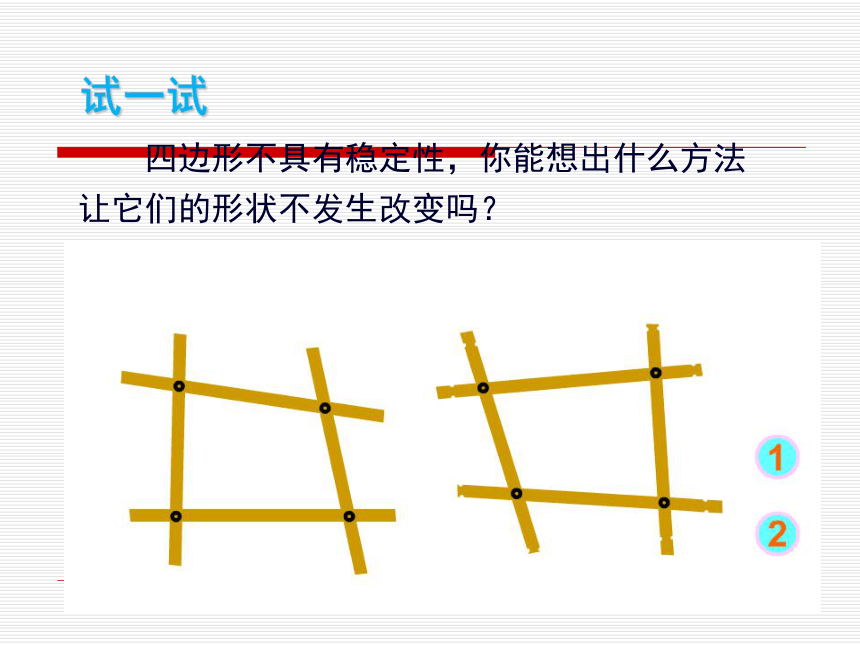
的形状会改变。只要三角形三边的长度确定了,这个三形的形状和大小就确定,三角形的这个性质叫三角形的稳定性。 做一做 四边形不具有稳定性,你能想出什么方法
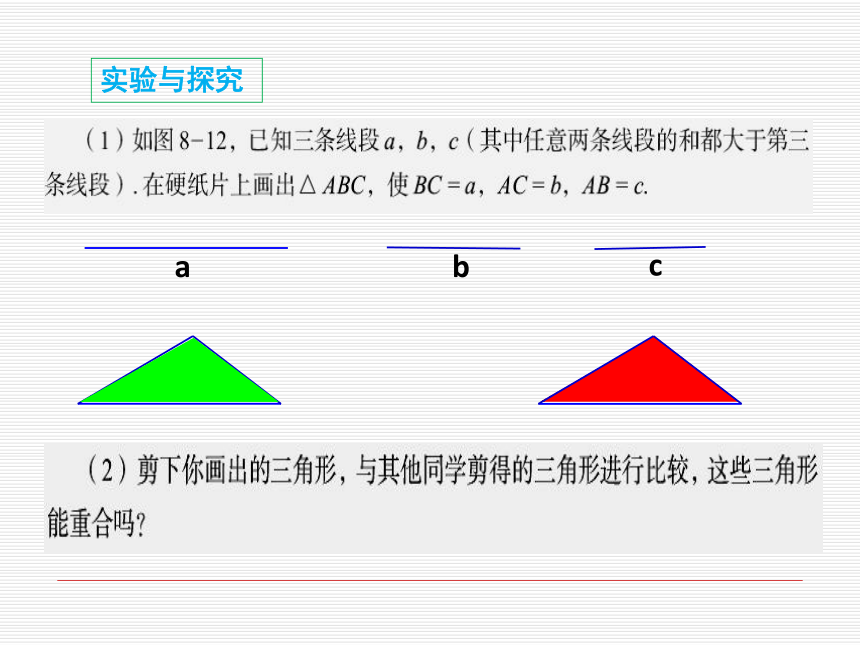
让它们的形状不发生改变吗? 试一试实验与探究abc结论 判定方法4
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。三边对应相等的两个三角形全等.
(简写成“边边边”或“SSS”)如何用符号语言来表达呢?≌结论点拨:欲证角相等,转化为证三角形全等。 例5练一练
1.如图所示, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
例62. 如图,AB=AD,CB=CD,E是AC上一点,BE与DE相等吗?练一练: 一定
(SAS)不一定 一定
(ASA) 一定
(AAS) 一定
(SSS)不一定归纳判定三角形全等至少要有一组边!
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
3.知道三角形的稳定性和四边形的不稳定性。 1.如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;判断两个三角形全等的条件:AB=AC∠BDA=∠CDA∠B=∠CSAS、ASA、AAS知识回顾 2. ,具备下列条件中的哪三个
条件就可判定三角形全等?和知识回顾 取出若干根的木条,把它们分别做成三角形和四边形框架,并拉动它们。你发现什么? 三角形的大小和形状是固定不变的,而四边形
的形状会改变。只要三角形三边的长度确定了,这个三形的形状和大小就确定,三角形的这个性质叫三角形的稳定性。 做一做 四边形不具有稳定性,你能想出什么方法
让它们的形状不发生改变吗? 试一试实验与探究abc结论 判定方法4
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。三边对应相等的两个三角形全等.
(简写成“边边边”或“SSS”)如何用符号语言来表达呢?≌结论点拨:欲证角相等,转化为证三角形全等。 例5练一练
1.如图所示, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
例62. 如图,AB=AD,CB=CD,E是AC上一点,BE与DE相等吗?练一练: 一定
(SAS)不一定 一定
(ASA) 一定
(AAS) 一定
(SSS)不一定归纳判定三角形全等至少要有一组边!
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
