1.5函数y=Asin(ωx+φ)的图象(二)
文档属性
| 名称 | 1.5函数y=Asin(ωx+φ)的图象(二) |  | |
| 格式 | rar | ||
| 文件大小 | 141.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-24 13:25:00 | ||
图片预览





文档简介
课件26张PPT。第二课时1.5 函数 的图象问题提出1.函数 图象是由函数 的图象经过怎样的变换而得到的? 的图象,可以看作是把正弦曲线 上所有的点向左(当
>0时)或向右(当 <0时)平行移动| |个单位长度而得到.2.函数 的图象是由函数
的图象经过怎样的变换而得到的? 函数 的图象,可以看作是把函数 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变)而得到的. 3.函数 的图象,不仅受 、 的影响,而且受A的影响,对此,我们再作进一步探究.振幅变换
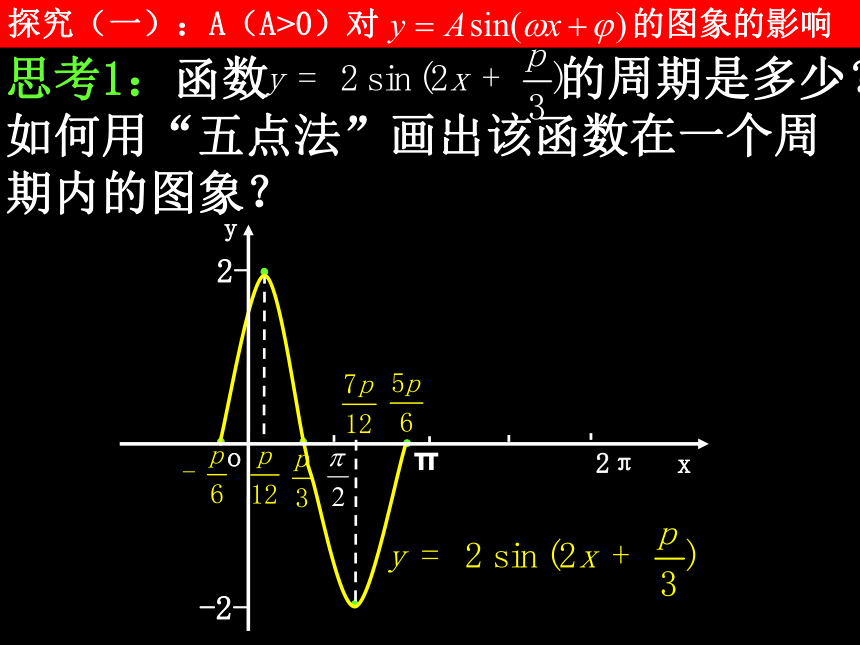
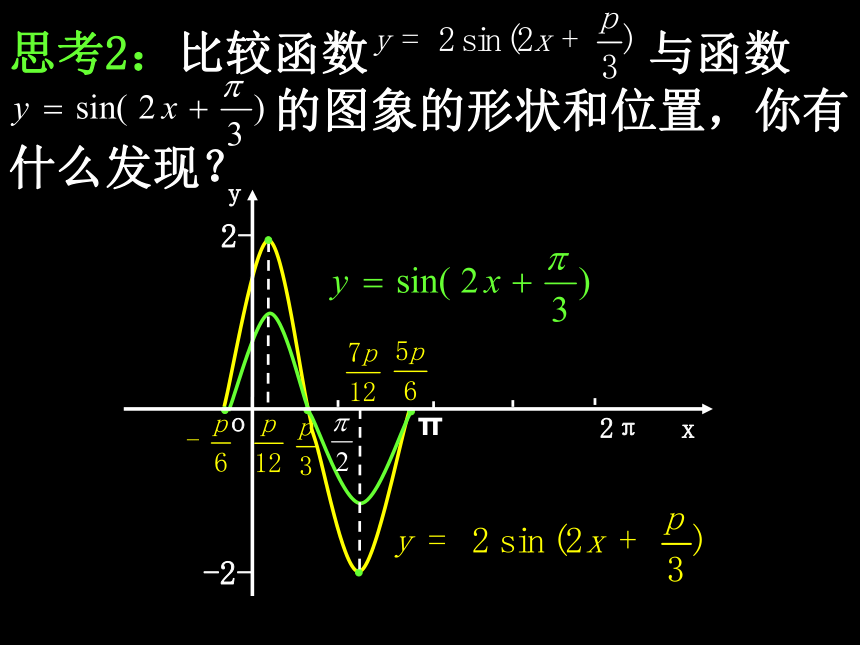
与综合变换探究(一):A(A>0)对 的图象的影响 思考1:函数 的周期是多少?如何用“五点法”画出该函数在一个周期内的图象? 思考2:比较函数 与函数
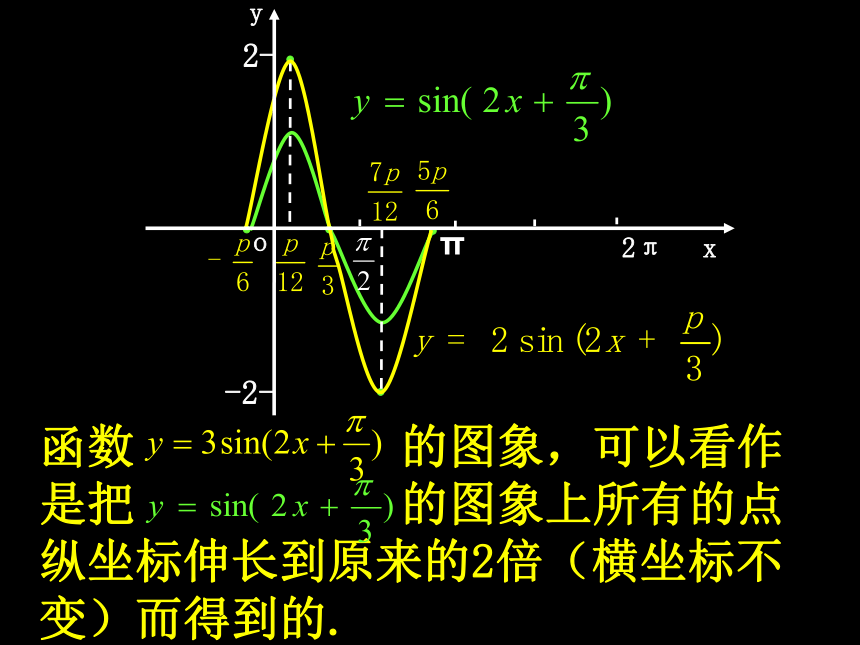
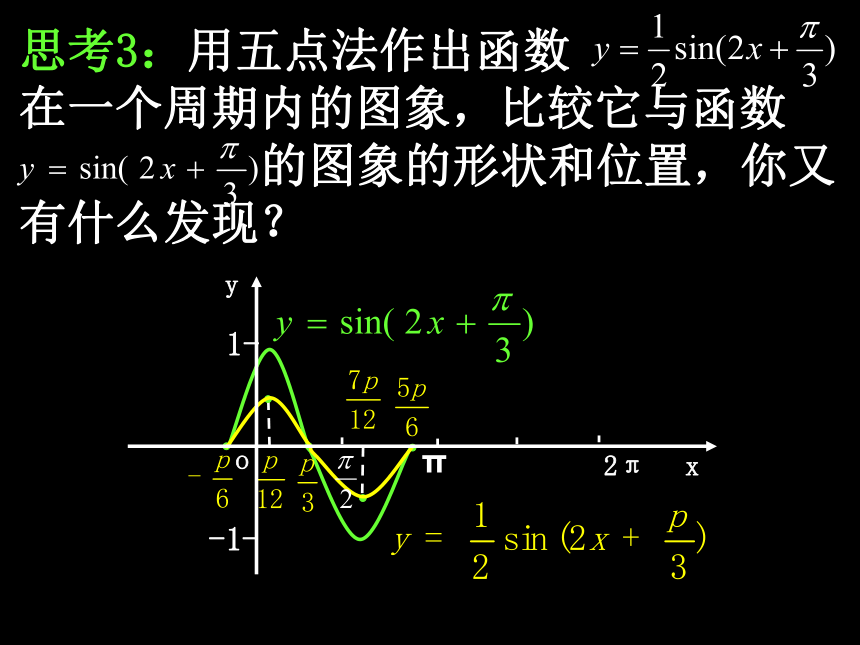
的图象的形状和位置,你有什么发现? 函数 的图象,可以看作是把 的图象上所有的点纵坐标伸长到原来的2倍(横坐标不变)而得到的. 思考3:用五点法作出函数 在一个周期内的图象,比较它与函数
的图象的形状和位置,你又有什么发现? 函数 的图象,可以看作是把 的图象上所有的点纵坐标缩短到原来的 倍(横坐标不变)而得到的.思考4:一般地,对任意的A(A>0且A≠1),函数 的图象是由函数 的图象经过怎样的变换而得到的? 函数 的图象,可以看作是把函数 的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)而得到的. 思考5:上述变换称为振幅变换,据此理论,函数 的图象是由
函数 的图象经过怎样的变换而得到的? 函数 的图象,可以看作是
把 的图象上所有的点纵坐标伸长到原来的1.5倍(横坐标不变)而得到的. 探究(二): 与 的图象关系 思考2:你能设计一个变换过程完成上述变换吗?思考1:将函数 的图象经过几次变换,可以得到函数 的图象? 思考3:一般地,函数 (A>0, >0)的图象,可以由函数 的图象经过怎样的变换而得到? 先把函数 的图象向左(右)平移| |个单位长度,得到函数 的图象;再把曲线上各点的横坐标变为原来的 倍,得到函数 的图象;然后把曲线上各点的纵坐标变为原来的A倍,就得到函数 的图象.思考4:将函数 的图象变换到函数 (其中A>0, >0)的图象,共有多少种不同的变换次序? 6种!思考5:若将函数 的图象先作振幅变换,再作周期变换,然后作平移变换得到函数 的图象,具体如何操作? .exe思考6:物理中,简谐运动的图象就是函数 , 的图象,其中A>0, >0.描述简谐运动的物理量有振幅、周期、频率、相位和初相等,你知道这些物理量分别是指那些数据以及各自的含义吗? 称为初相,即x=0时的相位.A是振幅,它是指物体离开平衡位置的最大距离; 是周期,它是指物体往复运动一次所需要的时间; 是频率,它是指物体在单位时间内往复运动的次数; 称为相位;理论迁移 例1 说明函数 的图象是由函数 的图象经过怎样的变换而得到的? 例2 如图是某简谐运动的图象,试根据图象回答下列问题: ⑴ 这个简谐运动的振幅、周期与频率各是多少? 振幅A=2周期T=0.8s频率f=1.25 ⑵ 从O点算起,到曲线上的哪一点,表示完成了一次往返运动?如从A点算起呢?O~DA~E ⑶ 写出这个简谐运动的表达式.小结作业1.函数 (A>0,>0)的图象,可以由函数 的图象通过三次变换而得到,共有6种不同的变换次序.在实际应用中,一般按“左右平移→横向伸缩→纵向伸缩”的次序进行. 2.用“变换法”作函数 的图象,其作图过程较复杂,不便于操作,在一般情况下,常用“五点法”作图.3.通过平移,将函数 的图象变换为 的图象,其平移单位是 .4.若已知函数 的图象及有关数字特征,则可以求出函数的解析式.作业:
P56 练习:3,4.
P58习题1.5A组:4,5.
>0时)或向右(当 <0时)平行移动| |个单位长度而得到.2.函数 的图象是由函数
的图象经过怎样的变换而得到的? 函数 的图象,可以看作是把函数 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变)而得到的. 3.函数 的图象,不仅受 、 的影响,而且受A的影响,对此,我们再作进一步探究.振幅变换
与综合变换探究(一):A(A>0)对 的图象的影响 思考1:函数 的周期是多少?如何用“五点法”画出该函数在一个周期内的图象? 思考2:比较函数 与函数
的图象的形状和位置,你有什么发现? 函数 的图象,可以看作是把 的图象上所有的点纵坐标伸长到原来的2倍(横坐标不变)而得到的. 思考3:用五点法作出函数 在一个周期内的图象,比较它与函数
的图象的形状和位置,你又有什么发现? 函数 的图象,可以看作是把 的图象上所有的点纵坐标缩短到原来的 倍(横坐标不变)而得到的.思考4:一般地,对任意的A(A>0且A≠1),函数 的图象是由函数 的图象经过怎样的变换而得到的? 函数 的图象,可以看作是把函数 的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)而得到的. 思考5:上述变换称为振幅变换,据此理论,函数 的图象是由
函数 的图象经过怎样的变换而得到的? 函数 的图象,可以看作是
把 的图象上所有的点纵坐标伸长到原来的1.5倍(横坐标不变)而得到的. 探究(二): 与 的图象关系 思考2:你能设计一个变换过程完成上述变换吗?思考1:将函数 的图象经过几次变换,可以得到函数 的图象? 思考3:一般地,函数 (A>0, >0)的图象,可以由函数 的图象经过怎样的变换而得到? 先把函数 的图象向左(右)平移| |个单位长度,得到函数 的图象;再把曲线上各点的横坐标变为原来的 倍,得到函数 的图象;然后把曲线上各点的纵坐标变为原来的A倍,就得到函数 的图象.思考4:将函数 的图象变换到函数 (其中A>0, >0)的图象,共有多少种不同的变换次序? 6种!思考5:若将函数 的图象先作振幅变换,再作周期变换,然后作平移变换得到函数 的图象,具体如何操作? .exe思考6:物理中,简谐运动的图象就是函数 , 的图象,其中A>0, >0.描述简谐运动的物理量有振幅、周期、频率、相位和初相等,你知道这些物理量分别是指那些数据以及各自的含义吗? 称为初相,即x=0时的相位.A是振幅,它是指物体离开平衡位置的最大距离; 是周期,它是指物体往复运动一次所需要的时间; 是频率,它是指物体在单位时间内往复运动的次数; 称为相位;理论迁移 例1 说明函数 的图象是由函数 的图象经过怎样的变换而得到的? 例2 如图是某简谐运动的图象,试根据图象回答下列问题: ⑴ 这个简谐运动的振幅、周期与频率各是多少? 振幅A=2周期T=0.8s频率f=1.25 ⑵ 从O点算起,到曲线上的哪一点,表示完成了一次往返运动?如从A点算起呢?O~DA~E ⑶ 写出这个简谐运动的表达式.小结作业1.函数 (A>0,>0)的图象,可以由函数 的图象通过三次变换而得到,共有6种不同的变换次序.在实际应用中,一般按“左右平移→横向伸缩→纵向伸缩”的次序进行. 2.用“变换法”作函数 的图象,其作图过程较复杂,不便于操作,在一般情况下,常用“五点法”作图.3.通过平移,将函数 的图象变换为 的图象,其平移单位是 .4.若已知函数 的图象及有关数字特征,则可以求出函数的解析式.作业:
P56 练习:3,4.
P58习题1.5A组:4,5.
