5.1.2垂线课件
图片预览





文档简介
课件16张PPT。在相交线的模型中,固定木条a,转动木条b,当α =90°时,会有特殊情况出现,a、b所成的四个角有什么特殊关系? 当b的位置变化时,a、b所成的角α也会发生变化.α α 创设情景 明确目标答:当 α =90° 时, a、b所成的四个角相等,都是90°合作探究 达成目标知识点一:垂线的概念阅读教材第3页至4页,思考下列问题:
两条相交直线在什么情况下是垂直的?
什么叫垂线?什么叫垂足?
2.垂线是一条直线还是线段?
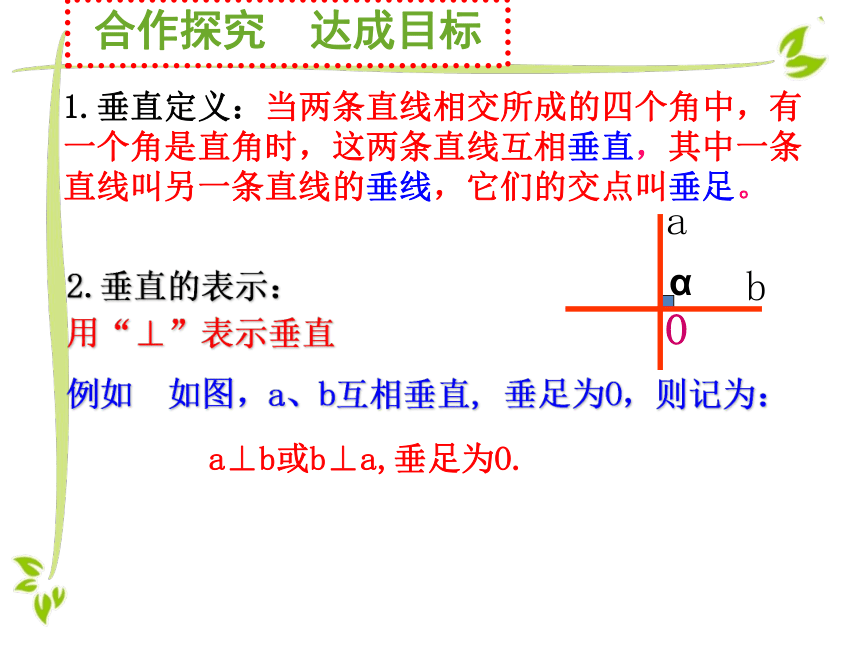
3.请举出生活中垂直的例子。1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”表示垂直Oα 2.垂直的表示:例如 如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a,垂足为O. 合作探究 达成目标合作探究 达成目标日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?ABCDO书写形式:如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式:反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。②性质:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)3.垂直的运用:合作探究 达成目标
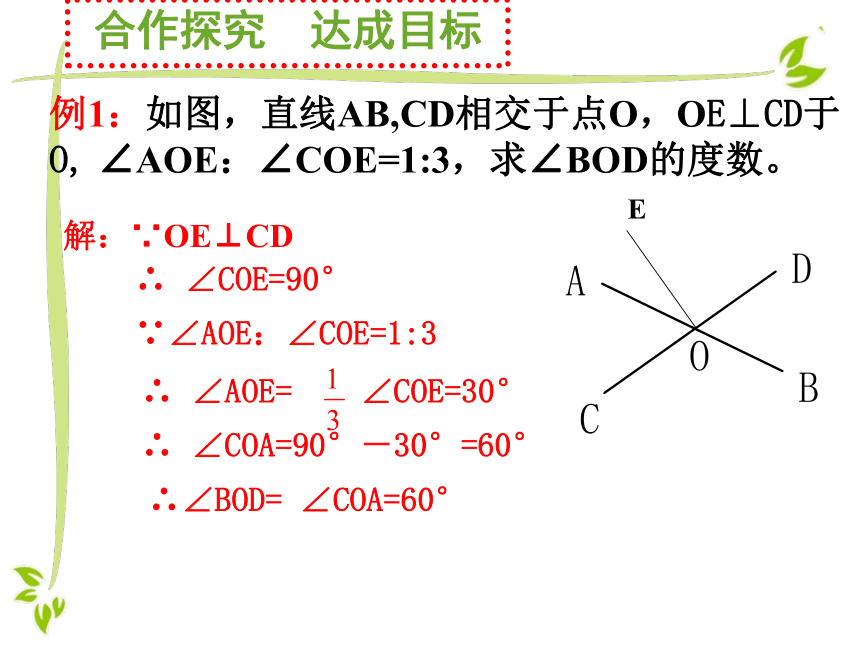
例1:如图,直线AB,CD相交于点O,OE⊥CD于O, ∠AOE:∠COE=1:3,求∠BOD的度数。解:∵OE⊥CD
∴ ∠COE=90°∵∠AOE:∠COE=1:3∴ ∠AOE= ∠COE=30°∴ ∠COA=90°-30°=60°∴∠BOD= ∠COA=60°合作探究 达成目标
变式:如图,直线AB,CD相交于点O,若AO平分∠COE,且∠BOD=45°,判断OE与CD的位置关系,并说明理由。解:OE⊥ CD合作探究 达成目标知识点二:垂线的公理问题:
怎么样画垂线?问题:
这样画l的垂线可以画几条?lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B则所画直线AB是过点A的直线l的垂线.请同学们画一下1.垂线的画法: 结论: 在同一平面内,过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条?垂线公理P ·.AB(2)(1)ABP·(3)如图,请你过点P画出线段AB或射线AB的垂线。解:如图所示学以致用课堂总结1、两条直线相交,所成四个角中有一个角是_____时,
我们称这两条直线__________,其中一条直线是另
一条直线的_____ ___,他们的交点叫做_____ ____。
垂直用符号____来表示
2、过一点有且只有_________直线与已知直线垂直。
3、垂线的画法:——————————————————
直角互相垂直垂线垂足⊥一条一放 ,二靠 ,三移,四画线
课本:习题5.1第4,5,12题;
两条相交直线在什么情况下是垂直的?
什么叫垂线?什么叫垂足?
2.垂线是一条直线还是线段?
3.请举出生活中垂直的例子。1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”表示垂直Oα 2.垂直的表示:例如 如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a,垂足为O. 合作探究 达成目标合作探究 达成目标日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?ABCDO书写形式:如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式:反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。②性质:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)3.垂直的运用:合作探究 达成目标
例1:如图,直线AB,CD相交于点O,OE⊥CD于O, ∠AOE:∠COE=1:3,求∠BOD的度数。解:∵OE⊥CD
∴ ∠COE=90°∵∠AOE:∠COE=1:3∴ ∠AOE= ∠COE=30°∴ ∠COA=90°-30°=60°∴∠BOD= ∠COA=60°合作探究 达成目标
变式:如图,直线AB,CD相交于点O,若AO平分∠COE,且∠BOD=45°,判断OE与CD的位置关系,并说明理由。解:OE⊥ CD合作探究 达成目标知识点二:垂线的公理问题:
怎么样画垂线?问题:
这样画l的垂线可以画几条?lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B则所画直线AB是过点A的直线l的垂线.请同学们画一下1.垂线的画法: 结论: 在同一平面内,过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条?垂线公理P ·.AB(2)(1)ABP·(3)如图,请你过点P画出线段AB或射线AB的垂线。解:如图所示学以致用课堂总结1、两条直线相交,所成四个角中有一个角是_____时,
我们称这两条直线__________,其中一条直线是另
一条直线的_____ ___,他们的交点叫做_____ ____。
垂直用符号____来表示
2、过一点有且只有_________直线与已知直线垂直。
3、垂线的画法:——————————————————
直角互相垂直垂线垂足⊥一条一放 ,二靠 ,三移,四画线
课本:习题5.1第4,5,12题;
