北师大版九年级数学上册4.6利用相似三角形测高测试卷(解析版)
文档属性
| 名称 | 北师大版九年级数学上册4.6利用相似三角形测高测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 23:43:59 | ||
图片预览



文档简介
北师大版九年级数学上册4.6《利用相似三角形测高》测试卷
一.选择题(共10小题)
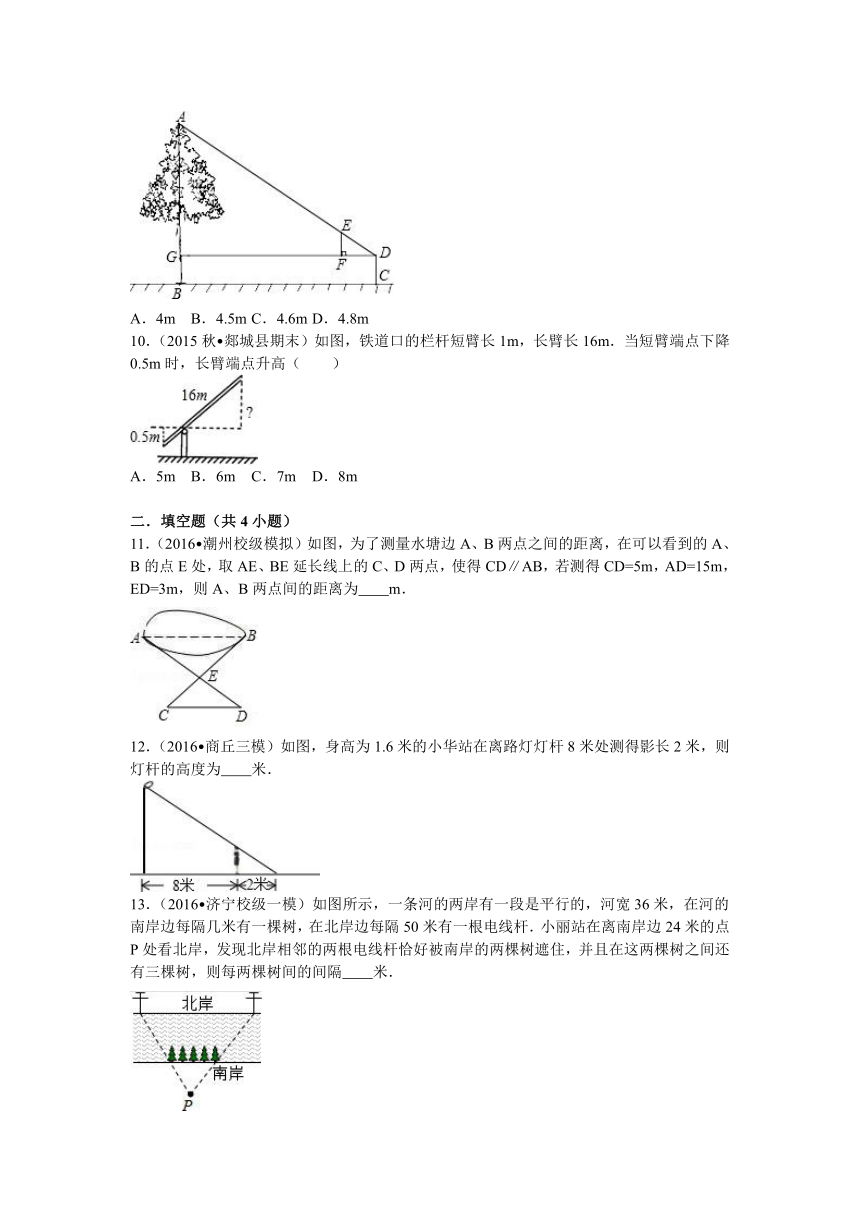
1.(2016 河西区模拟)阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
A.4米
B.3.8米
C.3.6米
D.3.4米
2.(2016 承德模拟)在某一时刻,测得一根高为1.2m的木棍的影长为2m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.15m
B.m
C.60
m
D.24m
3.(2016 上城区二模)如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
A.6米
B.4.5米
C.4米
D.3米
4.(2016 崇明县一模)如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张
B.第5张
C.第6张
D.第7张
5.(2016 石景山区二模)如图,为了估计河的宽度,在河的对岸选定一个目标点A,在近岸取点B,C,D,E,使点A,B,D
在一条直线上,且AD⊥DE,点A,C,E也在一条直线上且DE∥BC.如果BC=24m,BD=12m,DE=40m,则河的宽度AB约为( )
A.20m
B.18m
C.28m
D.30m
6.(2016 兰州模拟)如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
A.
B.
C.
D.
7.(2015 聊城模拟)如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25m
B.4.25m
C.4.45m
D.4.75m
8.(2015 乐陵市模拟)三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是( )
A.5:2
B.2:5
C.4:25
D.25:4
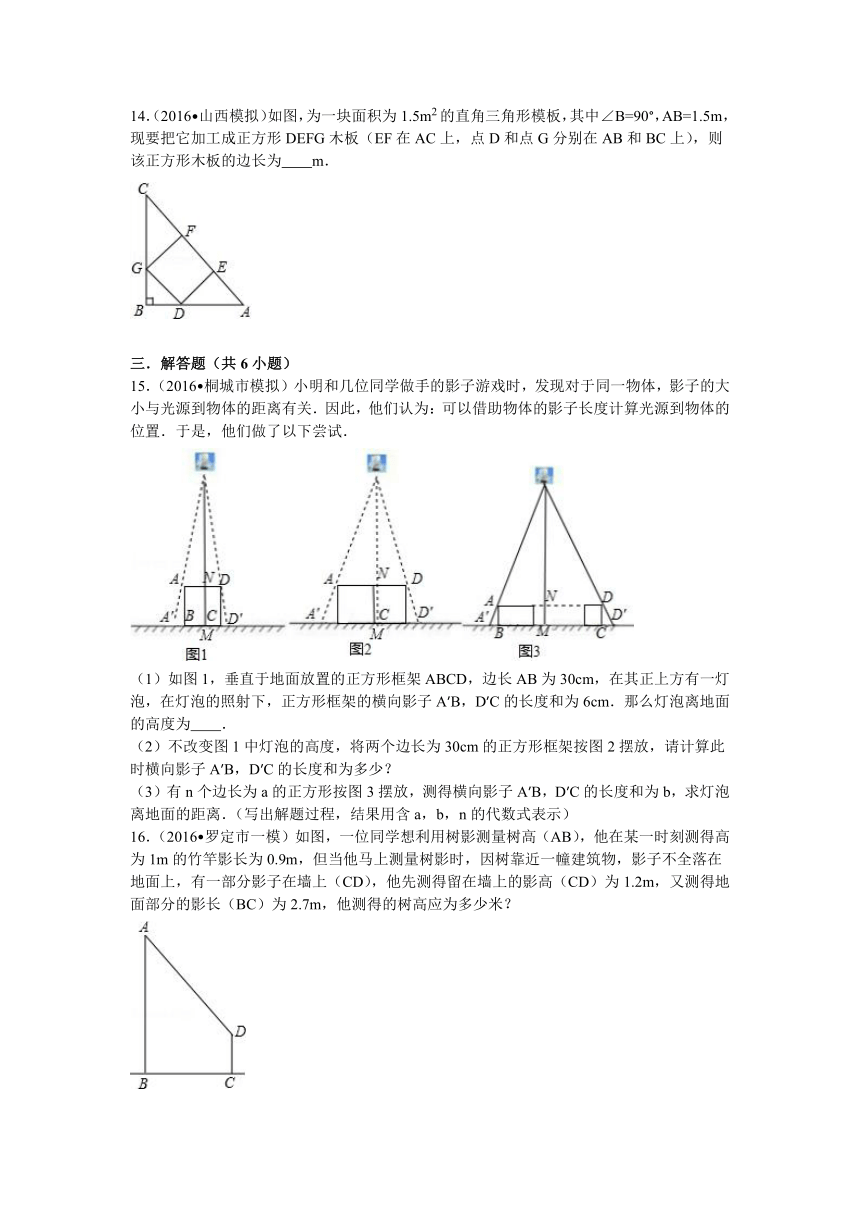
9.(2015 兰州模拟)如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )
A.4m
B.4.5m
C.4.6m
D.4.8m
10.(2015秋 郯城县期末)如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )
A.5m
B.6m
C.7m
D.8m
二.填空题(共4小题)
11.(2016 潮州校级模拟)如图,为了测量水塘边A、B两点之间的距离,在可以看到的A、B的点E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,AD=15m,ED=3m,则A、B两点间的距离为 m.
12.(2016 商丘三模)如图,身高为1.6米的小华站在离路灯灯杆8米处测得影长2米,则灯杆的高度为 米.
13.(2016 济宁校级一模)如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔 米.
14.(2016 山西模拟)如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为 m.
三.解答题(共6小题)
15.(2016 桐城市模拟)小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
16.(2016 罗定市一模)如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
17.(2016 蓝田县一模)如图,A、B两点被池塘隔开,小吴为了测量A,B两点间的距离,他在AB外选一点C,连接AC和BC,延长AC到D,使CD=AC,延长BC到E,使CE=BC,连接DE.若小吴测得DE的长为400米,根据以上信息,请你求出AB的长.
18.(2016 太原三模)对数(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是 ;
(2)在(1)中提到刘嶶的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
19.(2016春 滨海县校级月考)如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
20.(2016 岱岳区校级模拟)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 河西区模拟)阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
A.4米
B.3.8米
C.3.6米
D.3.4米
【分析】作辅助线,连接AE和BD,根据题意知:=,可将窗口底边离地面的高BC求出.
【解答】解:连接AE、BD,
∵光是沿直线传播的,
∴AE∥BD,
∴△BCD∽△ACE,
∴=
即=
解得:BC=4.
故选A.
【点评】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,求解即可.
2.(2016 承德模拟)在某一时刻,测得一根高为1.2m的木棍的影长为2m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.15m
B.m
C.60
m
D.24m
【分析】根据同时同地物高与影长成正比列出比例式求解即可.
【解答】解:设旗杆的高度为xm,
由题意得,=,
解得x=15,
答:这根旗杆的高度为15m.
故选A.
【点评】本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,需熟记.
3.(2016 上城区二模)如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
A.6米
B.4.5米
C.4米
D.3米
【分析】如图,CE=1.5m,易证得△ACE∽△ABD,根据相似三角形的性质得到=,然后利用比例性质求出BD即可.
【解答】解:如图,CE=1.5m,
∵CE∥BD,
∴△ACE∽△ABD,
∴=,即=,
∴BD=4.5(m),
即树的高度为4.5m.
故选B.
【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.
4.(2016 崇明县一模)如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张
B.第5张
C.第6张
D.第7张
【分析】根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
【解答】解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是3,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则,解得x=3,
所以另一段长为18﹣3=15,
因为15÷3=5,所以是第5张.
故选:B.
【点评】本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.
5.(2016 石景山区二模)如图,为了估计河的宽度,在河的对岸选定一个目标点A,在近岸取点B,C,D,E,使点A,B,D
在一条直线上,且AD⊥DE,点A,C,E也在一条直线上且DE∥BC.如果BC=24m,BD=12m,DE=40m,则河的宽度AB约为( )
A.20m
B.18m
C.28m
D.30m
【分析】先证明△ABC∽△ADE,利用相似比得到=,然后根据比例的性质求AB的长度.
【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
即=,
∴AB=18(m).
故选B.
【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.
6.(2016 兰州模拟)如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
A.
B.
C.
D.
【分析】根据反射的性质,可得β,根据余角的性质,可得∠1与∠2的关系,根据相似三角形的判定与性质,可得CE的长,根据正切函数,可得答案.
【解答】解:设CE的长为x,如图,
,
由入射角等于反射角,得
∠β=∠α,
由余角的性质,得
∠1=∠2.
由AC⊥CD,BD⊥CD,得
∠ACE=∠BDE,
△ACE∽△BDE,
=,即=,
解得x=
由题意,得
∠A=∠α.
tanα=tan∠A===,
故选:A.
【点评】本题考查了相似三角形的判定与性质,利用相似三角形的判定与性质得出CE的长是解题关键.
7.(2015 聊城模拟)如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25m
B.4.25m
C.4.45m
D.4.75m
【分析】此题首先要知道在同一时刻任何物体的高与其影子的比值是相同的,所以竹竿的高与其影子的比值和树高与其影子的比值相同,利用这个结论可以求出树高.
【解答】解:如图,设BD是BC在地面的影子,树高为x,
根据竹竿的高与其影子的比值和树高与其影子的比值相同得而CB=1.2,
∴BD=0.96,
∴树在地面的实际影子长是0.96+2.6=3.56,
再竹竿的高与其影子的比值和树高与其影子的比值相同得,
∴x=4.45,
∴树高是4.45m.
故选C.
【点评】解题的关键要知道竹竿的高与其影子的比值和树高与其影子的比值相同.
8.(2015 乐陵市模拟)三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是( )
A.5:2
B.2:5
C.4:25
D.25:4
【分析】先根据相似三角形对应边成比例求出三角尺与影子的相似比,再根据相似三角形周长的比等于相似比解答即可.
【解答】解:如图,∵OA=20cm,OA′=50cm,
∴===,
∵三角尺与影子是相似三角形,
∴三角尺的周长与它在墙上形成的影子的周长的比==2:5.
故选:B.
【点评】本题考查了相似三角形的应用,注意利用了相似三角形对应边成比例的性质,周长的比等于相似比的性质.
9.(2015 兰州模拟)如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )
A.4m
B.4.5m
C.4.6m
D.4.8m
【分析】先证明△DEF∽△DAB,利用相似比计算出AG,然后计算AG+GB即可得到AB的长.
【解答】解:如图,BG=DC=1m,DG=7.5m,
∵EF∥AG,
∴△DEF∽△DAB,
∴=,即=,
∴AG=3,
∴AB=BG+AG=1+3=4(m).
故选A.
【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.
10.(2015秋 郯城县期末)如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )
A.5m
B.6m
C.7m
D.8m
【分析】栏杆长短臂在升降过程中,将形成两个相似三角形,利用对应变成比例解题.
【解答】解:设长臂端点升高x米,
则,
∴x=8.
故选D.
【点评】此题是相似三角形在实际生活中的运用,比较简单.
二.填空题(共4小题)
11.(2016 潮州校级模拟)如图,为了测量水塘边A、B两点之间的距离,在可以看到的A、B的点E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,AD=15m,ED=3m,则A、B两点间的距离为 m.
【分析】根据CD∥AB可得△CDE∽△BAE,再根据其相似比解答.
【解答】解:∵CD∥AB,
∴△ABE∽△DCE,
∴CD:AB=DE:AE,
∴5:AB=3:12,
∴AB=20m.
答:A、B两点间的距离为20m.
【点评】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出A、B两点间的距离,体现了方程的思想.
12.(2016 商丘三模)如图,身高为1.6米的小华站在离路灯灯杆8米处测得影长2米,则灯杆的高度为 米.
【分析】根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似解答.
【解答】解:如图:
∵AB∥CD,
∴CD:AB=CE:BE,
∴1.6:AB=2:10,
∴AB=8米,
∴灯杆的高度为8米.
答:灯杆的高度为8米.
【点评】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出灯杆的高度,体现了方程的思想.
13.(2016 济宁校级一模)如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔 米.
【分析】根据题意,河两岸平行,故可得△ABP∽△DPC,根据相似三角形对应高的比等于相似比,列出方程,求解即可.
【解答】解:如图,过点P作PE⊥DC,交AB于点F,
设每两棵树间的间隔xm,根据题意可得:
∵AB∥CD
∴△ABP∽△DPC,
∴=,
∴=,
解得:x=5,
故答案为:5.
【点评】本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
14.(2016 山西模拟)如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为 m.
【分析】直接利用勾股定理结合直角三角形的性质得出BN的长,再利用相似三角形的判定与性质表示出AD的长,进而得出答案.
【解答】解:过点B作BN⊥AC于点N,
∵面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,
∴BC=2cm,
∴AC==2.5(m),
∴2.5BN=1.5×2,
解得:BN=1.2,
∵∠A=∠A,∠AED=∠ABC,
∴△AED∽△ABC,
∴=,
设DE=x,
则=,
解得:AD=x,
∵DG∥AC,
∴△GBD∽△CBA,
∴=
∴=
解得:x=.
故该正方形木板的边长为m.
故答案为:.
【点评】此题主要考查了相似三角形的应用以及勾股定理的应用,正确表示出AD的长是解题关键.
三.解答题(共6小题)
15.(2016 桐城市模拟)小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
【分析】(1)设灯泡的位置为点P,易得△PAD∽△PA′D′,设出所求的未知数,利用相似三角形的对应边的比等于对应高的比,可得灯泡离地面的高度;
(2)同法可得到横向影子A′B,D′C的长度和;
(3)按照相应的三角形相似,利用相似三角形的对应边的比等于对应高的比,用字母表示出其他线段,即可得到灯泡离地面的距离.
【解答】解:(1)设灯泡离地面的高度为xcm,
∵AD∥A′D′,
∴∠PAD=∠PA′D′,∠PDA=∠PD′A′.
∴△PAD∽△PA′D′.
根据相似三角形对应高的比等于相似比的性质,可得,
∴=,
解得x=180.(4分)
(2)设横向影子A′B,D′C的长度和为ycm,
同理可得∴=,
解得y=12cm;(3分)
(3)记灯泡为点P,如图:
∵AD∥A′D′,∴∠PAD=∠PA′D′,∠PDA=∠PD′A′.
∴△PAD∽△PA′D′.
根据相似三角形对应高的比等于相似比的性质,可得(1分)
(直接得出三角形相似或比例线段均不扣分)
设灯泡离地面距离为x,由题意,得PM=x,PN=x﹣a,AD=na,A′D′=na+b,
∴=1﹣
=1﹣
x=(1分).
【点评】本题主要考查相似三角形的判定与性质,注意运用相似三角形对应高的比等于相似比这个性质.
16.(2016 罗定市一模)如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
【分析】先求出墙上的影高CD落在地面上时的长度,再设树高为h,根据同一时刻物高与影长成正比列出关系式求出h的值即可.
【解答】解:过D作DE∥BC交AB于点E,
设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的竹竿影长为0.9m,墙上的影高CD为1.2m,
∴=,解得x=1.08(m),
∴树的影长为:1.08+2.7=3.78(m),
∴=,解得h=4.2(m).
答:测得的树高为4.2米.
【点评】本题考查的是相似三角形的应用,解答此题的关键是正确求出树的影长,这是此题的易错点.
17.(2016 蓝田县一模)如图,A、B两点被池塘隔开,小吴为了测量A,B两点间的距离,他在AB外选一点C,连接AC和BC,延长AC到D,使CD=AC,延长BC到E,使CE=BC,连接DE.若小吴测得DE的长为400米,根据以上信息,请你求出AB的长.
【分析】根据题意结合相似三角形的判定方法得出,△ABC∽△DEC,进而求出AB的长.
【解答】解:∵CD=AC,CE=BC,
∴==,
∵∠ACB=∠ECD,
∴△ABC∽△DEC,
∴==,
∴AB=800,
答:AB的长为800m.
【点评】此题主要考查了相似三角形的应用,正确得出△ABC∽△DEC是解题关键.
18.(2016 太原三模)对数(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是 ;
(2)在(1)中提到刘嶶的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
【分析】(1)根据历史常识可得到答案;
(2)根据题意得出△FCB∽△FAH,△EDG∽△AHG,进而利用相似三角形的性质求出即可.
【解答】解:(1)《海岛算经》;
(2)由题意,得,AH⊥HG,CB⊥HG,
∴∠AHF=90°,∠CBF=90°,
∴∠AHF=∠CBF,
∵∠AFB=∠CFB,
∴△CBF∽△AHF,
∴=,
同理可得=,
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,
∴=,=,
解得HB=30750,HA=753,
答:AH为753丈,HB为30750步.
【点评】此题主要考查了相似三角形的应用,得出△FCB∽△FAH,△EDG∽△AHG是解题关键.
19.(2016春 滨海县校级月考)如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
【分析】(1)如图1,先证明△APM∽△ABD,利用相似比可得AP=AB,再证明△BQN∽△BAC,利用相似比可得BQ=AB,则AB+12+AB=AB,解得AB=18(m);
(2)如图1,他在路灯A下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得=,然后利用比例性质求出BN即可.
【解答】解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
=,即=,
∴AP=AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴=,即=,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴=,即=,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
【点评】本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
20.(2016 岱岳区校级模拟)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
【分析】(1)设正方形的边长为xmm,则PN=PQ=ED=x,AE=AD﹣ED=80﹣x,通过证明△APN∽△ABC,利用相似比可得到=,然后根据比例性质求出x即可;
(2)由于矩形是由两个并排放置的正方形所组成,则可设PQ=x,则PN=2x,AE=80﹣x,然后与(1)的方法一样求解;
(3)设PN=x,用PQ表示出AE的长度,然后根据相似三角形对应高的比等于相似比列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答.
【解答】解:(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD﹣ED=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得x=48.
∴加工成的正方形零件的边长是48mm;
(2)如图2,设PQ=x,则PN=2x,AE=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得:x=,
∴2x=,
∴这个矩形零件的两条边长分别为mm,mm;
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴=,
即=,
解得:PQ=80﹣x.
则S=PN PQ=x(80﹣x)=﹣x2+80x=﹣(x﹣60)2+2400,
故S的最大值为2400mm2,此时PN=60mm,PQ=80﹣×60=40(mm).
【点评】本题考查了相似三角形的应用,二次函数的最值问题,根据相似三角形对应高的比等于对应边的比列式表示出正方形的边长与三角形的边与这边上的高的关系是解题的关键.
一.选择题(共10小题)
1.(2016 河西区模拟)阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
A.4米
B.3.8米
C.3.6米
D.3.4米
2.(2016 承德模拟)在某一时刻,测得一根高为1.2m的木棍的影长为2m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.15m
B.m
C.60
m
D.24m
3.(2016 上城区二模)如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
A.6米
B.4.5米
C.4米
D.3米
4.(2016 崇明县一模)如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张
B.第5张
C.第6张
D.第7张
5.(2016 石景山区二模)如图,为了估计河的宽度,在河的对岸选定一个目标点A,在近岸取点B,C,D,E,使点A,B,D
在一条直线上,且AD⊥DE,点A,C,E也在一条直线上且DE∥BC.如果BC=24m,BD=12m,DE=40m,则河的宽度AB约为( )
A.20m
B.18m
C.28m
D.30m
6.(2016 兰州模拟)如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
A.
B.
C.
D.
7.(2015 聊城模拟)如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25m
B.4.25m
C.4.45m
D.4.75m
8.(2015 乐陵市模拟)三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是( )
A.5:2
B.2:5
C.4:25
D.25:4
9.(2015 兰州模拟)如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )
A.4m
B.4.5m
C.4.6m
D.4.8m
10.(2015秋 郯城县期末)如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )
A.5m
B.6m
C.7m
D.8m
二.填空题(共4小题)
11.(2016 潮州校级模拟)如图,为了测量水塘边A、B两点之间的距离,在可以看到的A、B的点E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,AD=15m,ED=3m,则A、B两点间的距离为 m.
12.(2016 商丘三模)如图,身高为1.6米的小华站在离路灯灯杆8米处测得影长2米,则灯杆的高度为 米.
13.(2016 济宁校级一模)如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔 米.
14.(2016 山西模拟)如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为 m.
三.解答题(共6小题)
15.(2016 桐城市模拟)小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
16.(2016 罗定市一模)如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
17.(2016 蓝田县一模)如图,A、B两点被池塘隔开,小吴为了测量A,B两点间的距离,他在AB外选一点C,连接AC和BC,延长AC到D,使CD=AC,延长BC到E,使CE=BC,连接DE.若小吴测得DE的长为400米,根据以上信息,请你求出AB的长.
18.(2016 太原三模)对数(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是 ;
(2)在(1)中提到刘嶶的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
19.(2016春 滨海县校级月考)如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
20.(2016 岱岳区校级模拟)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 河西区模拟)阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
A.4米
B.3.8米
C.3.6米
D.3.4米
【分析】作辅助线,连接AE和BD,根据题意知:=,可将窗口底边离地面的高BC求出.
【解答】解:连接AE、BD,
∵光是沿直线传播的,
∴AE∥BD,
∴△BCD∽△ACE,
∴=
即=
解得:BC=4.
故选A.
【点评】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,求解即可.
2.(2016 承德模拟)在某一时刻,测得一根高为1.2m的木棍的影长为2m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.15m
B.m
C.60
m
D.24m
【分析】根据同时同地物高与影长成正比列出比例式求解即可.
【解答】解:设旗杆的高度为xm,
由题意得,=,
解得x=15,
答:这根旗杆的高度为15m.
故选A.
【点评】本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,需熟记.
3.(2016 上城区二模)如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,则树的高度为( )
A.6米
B.4.5米
C.4米
D.3米
【分析】如图,CE=1.5m,易证得△ACE∽△ABD,根据相似三角形的性质得到=,然后利用比例性质求出BD即可.
【解答】解:如图,CE=1.5m,
∵CE∥BD,
∴△ACE∽△ABD,
∴=,即=,
∴BD=4.5(m),
即树的高度为4.5m.
故选B.
【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.
4.(2016 崇明县一模)如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张
B.第5张
C.第6张
D.第7张
【分析】根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
【解答】解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是3,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则,解得x=3,
所以另一段长为18﹣3=15,
因为15÷3=5,所以是第5张.
故选:B.
【点评】本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.
5.(2016 石景山区二模)如图,为了估计河的宽度,在河的对岸选定一个目标点A,在近岸取点B,C,D,E,使点A,B,D
在一条直线上,且AD⊥DE,点A,C,E也在一条直线上且DE∥BC.如果BC=24m,BD=12m,DE=40m,则河的宽度AB约为( )
A.20m
B.18m
C.28m
D.30m
【分析】先证明△ABC∽△ADE,利用相似比得到=,然后根据比例的性质求AB的长度.
【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
即=,
∴AB=18(m).
故选B.
【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.
6.(2016 兰州模拟)如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
A.
B.
C.
D.
【分析】根据反射的性质,可得β,根据余角的性质,可得∠1与∠2的关系,根据相似三角形的判定与性质,可得CE的长,根据正切函数,可得答案.
【解答】解:设CE的长为x,如图,
,
由入射角等于反射角,得
∠β=∠α,
由余角的性质,得
∠1=∠2.
由AC⊥CD,BD⊥CD,得
∠ACE=∠BDE,
△ACE∽△BDE,
=,即=,
解得x=
由题意,得
∠A=∠α.
tanα=tan∠A===,
故选:A.
【点评】本题考查了相似三角形的判定与性质,利用相似三角形的判定与性质得出CE的长是解题关键.
7.(2015 聊城模拟)如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25m
B.4.25m
C.4.45m
D.4.75m
【分析】此题首先要知道在同一时刻任何物体的高与其影子的比值是相同的,所以竹竿的高与其影子的比值和树高与其影子的比值相同,利用这个结论可以求出树高.
【解答】解:如图,设BD是BC在地面的影子,树高为x,
根据竹竿的高与其影子的比值和树高与其影子的比值相同得而CB=1.2,
∴BD=0.96,
∴树在地面的实际影子长是0.96+2.6=3.56,
再竹竿的高与其影子的比值和树高与其影子的比值相同得,
∴x=4.45,
∴树高是4.45m.
故选C.
【点评】解题的关键要知道竹竿的高与其影子的比值和树高与其影子的比值相同.
8.(2015 乐陵市模拟)三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是( )
A.5:2
B.2:5
C.4:25
D.25:4
【分析】先根据相似三角形对应边成比例求出三角尺与影子的相似比,再根据相似三角形周长的比等于相似比解答即可.
【解答】解:如图,∵OA=20cm,OA′=50cm,
∴===,
∵三角尺与影子是相似三角形,
∴三角尺的周长与它在墙上形成的影子的周长的比==2:5.
故选:B.
【点评】本题考查了相似三角形的应用,注意利用了相似三角形对应边成比例的性质,周长的比等于相似比的性质.
9.(2015 兰州模拟)如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )
A.4m
B.4.5m
C.4.6m
D.4.8m
【分析】先证明△DEF∽△DAB,利用相似比计算出AG,然后计算AG+GB即可得到AB的长.
【解答】解:如图,BG=DC=1m,DG=7.5m,
∵EF∥AG,
∴△DEF∽△DAB,
∴=,即=,
∴AG=3,
∴AB=BG+AG=1+3=4(m).
故选A.
【点评】本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.
10.(2015秋 郯城县期末)如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )
A.5m
B.6m
C.7m
D.8m
【分析】栏杆长短臂在升降过程中,将形成两个相似三角形,利用对应变成比例解题.
【解答】解:设长臂端点升高x米,
则,
∴x=8.
故选D.
【点评】此题是相似三角形在实际生活中的运用,比较简单.
二.填空题(共4小题)
11.(2016 潮州校级模拟)如图,为了测量水塘边A、B两点之间的距离,在可以看到的A、B的点E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,AD=15m,ED=3m,则A、B两点间的距离为 m.
【分析】根据CD∥AB可得△CDE∽△BAE,再根据其相似比解答.
【解答】解:∵CD∥AB,
∴△ABE∽△DCE,
∴CD:AB=DE:AE,
∴5:AB=3:12,
∴AB=20m.
答:A、B两点间的距离为20m.
【点评】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出A、B两点间的距离,体现了方程的思想.
12.(2016 商丘三模)如图,身高为1.6米的小华站在离路灯灯杆8米处测得影长2米,则灯杆的高度为 米.
【分析】根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似解答.
【解答】解:如图:
∵AB∥CD,
∴CD:AB=CE:BE,
∴1.6:AB=2:10,
∴AB=8米,
∴灯杆的高度为8米.
答:灯杆的高度为8米.
【点评】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出灯杆的高度,体现了方程的思想.
13.(2016 济宁校级一模)如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔 米.
【分析】根据题意,河两岸平行,故可得△ABP∽△DPC,根据相似三角形对应高的比等于相似比,列出方程,求解即可.
【解答】解:如图,过点P作PE⊥DC,交AB于点F,
设每两棵树间的间隔xm,根据题意可得:
∵AB∥CD
∴△ABP∽△DPC,
∴=,
∴=,
解得:x=5,
故答案为:5.
【点评】本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
14.(2016 山西模拟)如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为 m.
【分析】直接利用勾股定理结合直角三角形的性质得出BN的长,再利用相似三角形的判定与性质表示出AD的长,进而得出答案.
【解答】解:过点B作BN⊥AC于点N,
∵面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,
∴BC=2cm,
∴AC==2.5(m),
∴2.5BN=1.5×2,
解得:BN=1.2,
∵∠A=∠A,∠AED=∠ABC,
∴△AED∽△ABC,
∴=,
设DE=x,
则=,
解得:AD=x,
∵DG∥AC,
∴△GBD∽△CBA,
∴=
∴=
解得:x=.
故该正方形木板的边长为m.
故答案为:.
【点评】此题主要考查了相似三角形的应用以及勾股定理的应用,正确表示出AD的长是解题关键.
三.解答题(共6小题)
15.(2016 桐城市模拟)小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
【分析】(1)设灯泡的位置为点P,易得△PAD∽△PA′D′,设出所求的未知数,利用相似三角形的对应边的比等于对应高的比,可得灯泡离地面的高度;
(2)同法可得到横向影子A′B,D′C的长度和;
(3)按照相应的三角形相似,利用相似三角形的对应边的比等于对应高的比,用字母表示出其他线段,即可得到灯泡离地面的距离.
【解答】解:(1)设灯泡离地面的高度为xcm,
∵AD∥A′D′,
∴∠PAD=∠PA′D′,∠PDA=∠PD′A′.
∴△PAD∽△PA′D′.
根据相似三角形对应高的比等于相似比的性质,可得,
∴=,
解得x=180.(4分)
(2)设横向影子A′B,D′C的长度和为ycm,
同理可得∴=,
解得y=12cm;(3分)
(3)记灯泡为点P,如图:
∵AD∥A′D′,∴∠PAD=∠PA′D′,∠PDA=∠PD′A′.
∴△PAD∽△PA′D′.
根据相似三角形对应高的比等于相似比的性质,可得(1分)
(直接得出三角形相似或比例线段均不扣分)
设灯泡离地面距离为x,由题意,得PM=x,PN=x﹣a,AD=na,A′D′=na+b,
∴=1﹣
=1﹣
x=(1分).
【点评】本题主要考查相似三角形的判定与性质,注意运用相似三角形对应高的比等于相似比这个性质.
16.(2016 罗定市一模)如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
【分析】先求出墙上的影高CD落在地面上时的长度,再设树高为h,根据同一时刻物高与影长成正比列出关系式求出h的值即可.
【解答】解:过D作DE∥BC交AB于点E,
设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的竹竿影长为0.9m,墙上的影高CD为1.2m,
∴=,解得x=1.08(m),
∴树的影长为:1.08+2.7=3.78(m),
∴=,解得h=4.2(m).
答:测得的树高为4.2米.
【点评】本题考查的是相似三角形的应用,解答此题的关键是正确求出树的影长,这是此题的易错点.
17.(2016 蓝田县一模)如图,A、B两点被池塘隔开,小吴为了测量A,B两点间的距离,他在AB外选一点C,连接AC和BC,延长AC到D,使CD=AC,延长BC到E,使CE=BC,连接DE.若小吴测得DE的长为400米,根据以上信息,请你求出AB的长.
【分析】根据题意结合相似三角形的判定方法得出,△ABC∽△DEC,进而求出AB的长.
【解答】解:∵CD=AC,CE=BC,
∴==,
∵∠ACB=∠ECD,
∴△ABC∽△DEC,
∴==,
∴AB=800,
答:AB的长为800m.
【点评】此题主要考查了相似三角形的应用,正确得出△ABC∽△DEC是解题关键.
18.(2016 太原三模)对数(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是 ;
(2)在(1)中提到刘嶶的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
【分析】(1)根据历史常识可得到答案;
(2)根据题意得出△FCB∽△FAH,△EDG∽△AHG,进而利用相似三角形的性质求出即可.
【解答】解:(1)《海岛算经》;
(2)由题意,得,AH⊥HG,CB⊥HG,
∴∠AHF=90°,∠CBF=90°,
∴∠AHF=∠CBF,
∵∠AFB=∠CFB,
∴△CBF∽△AHF,
∴=,
同理可得=,
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,
∴=,=,
解得HB=30750,HA=753,
答:AH为753丈,HB为30750步.
【点评】此题主要考查了相似三角形的应用,得出△FCB∽△FAH,△EDG∽△AHG是解题关键.
19.(2016春 滨海县校级月考)如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
【分析】(1)如图1,先证明△APM∽△ABD,利用相似比可得AP=AB,再证明△BQN∽△BAC,利用相似比可得BQ=AB,则AB+12+AB=AB,解得AB=18(m);
(2)如图1,他在路灯A下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得=,然后利用比例性质求出BN即可.
【解答】解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
=,即=,
∴AP=AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴=,即=,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴=,即=,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
【点评】本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
20.(2016 岱岳区校级模拟)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
【分析】(1)设正方形的边长为xmm,则PN=PQ=ED=x,AE=AD﹣ED=80﹣x,通过证明△APN∽△ABC,利用相似比可得到=,然后根据比例性质求出x即可;
(2)由于矩形是由两个并排放置的正方形所组成,则可设PQ=x,则PN=2x,AE=80﹣x,然后与(1)的方法一样求解;
(3)设PN=x,用PQ表示出AE的长度,然后根据相似三角形对应高的比等于相似比列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答.
【解答】解:(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD﹣ED=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得x=48.
∴加工成的正方形零件的边长是48mm;
(2)如图2,设PQ=x,则PN=2x,AE=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得:x=,
∴2x=,
∴这个矩形零件的两条边长分别为mm,mm;
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴=,
即=,
解得:PQ=80﹣x.
则S=PN PQ=x(80﹣x)=﹣x2+80x=﹣(x﹣60)2+2400,
故S的最大值为2400mm2,此时PN=60mm,PQ=80﹣×60=40(mm).
【点评】本题考查了相似三角形的应用,二次函数的最值问题,根据相似三角形对应高的比等于对应边的比列式表示出正方形的边长与三角形的边与这边上的高的关系是解题的关键.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
