北师大版七年级数学下册3.3用图象表示的变量间关系测试卷(解析版)
文档属性
| 名称 | 北师大版七年级数学下册3.3用图象表示的变量间关系测试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 565.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-10 00:00:00 | ||
图片预览

文档简介
北师大版七年级数学下册3.3《用图象表示的变量间关系》
测
试
卷
一.选择题(共10小题)
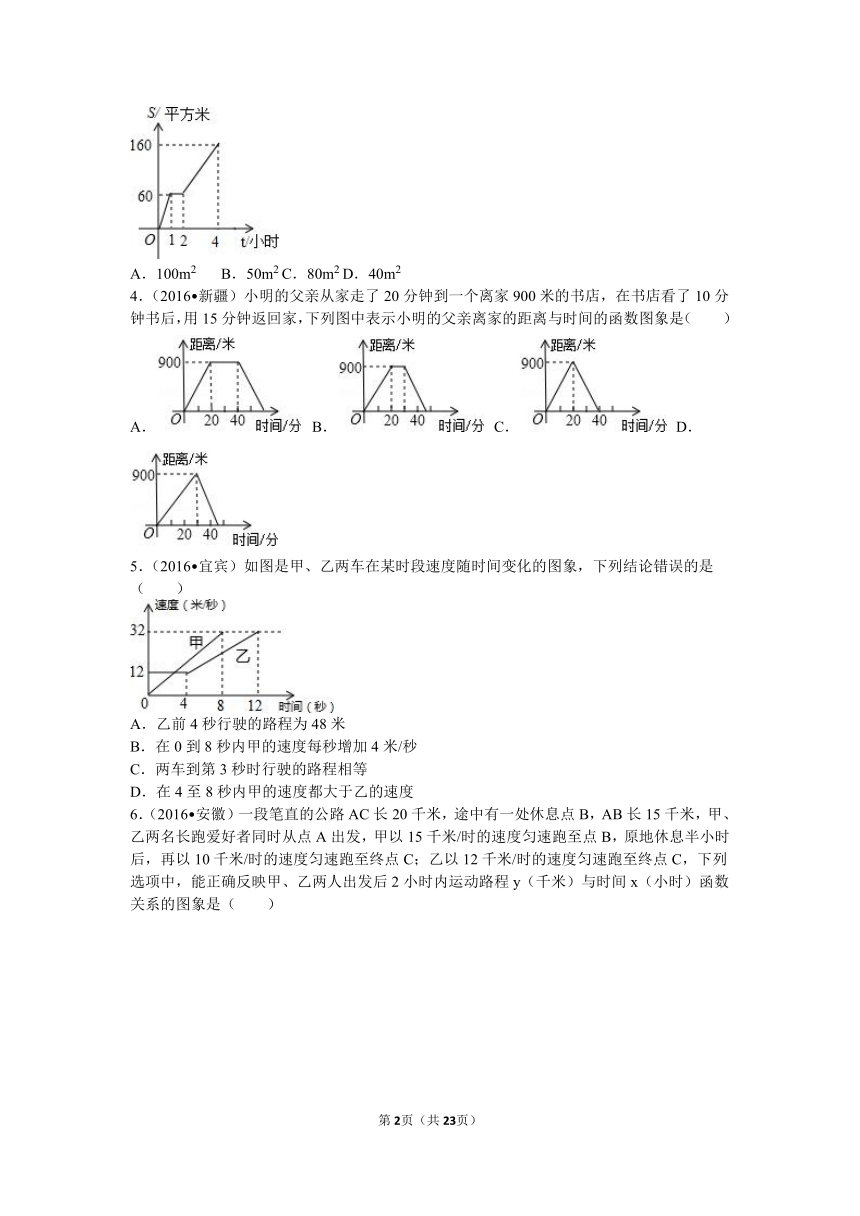
1.(2016 贵阳)星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A.
B.
C.
D.
2.(2016 衢州)如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.
B.
C.
D.
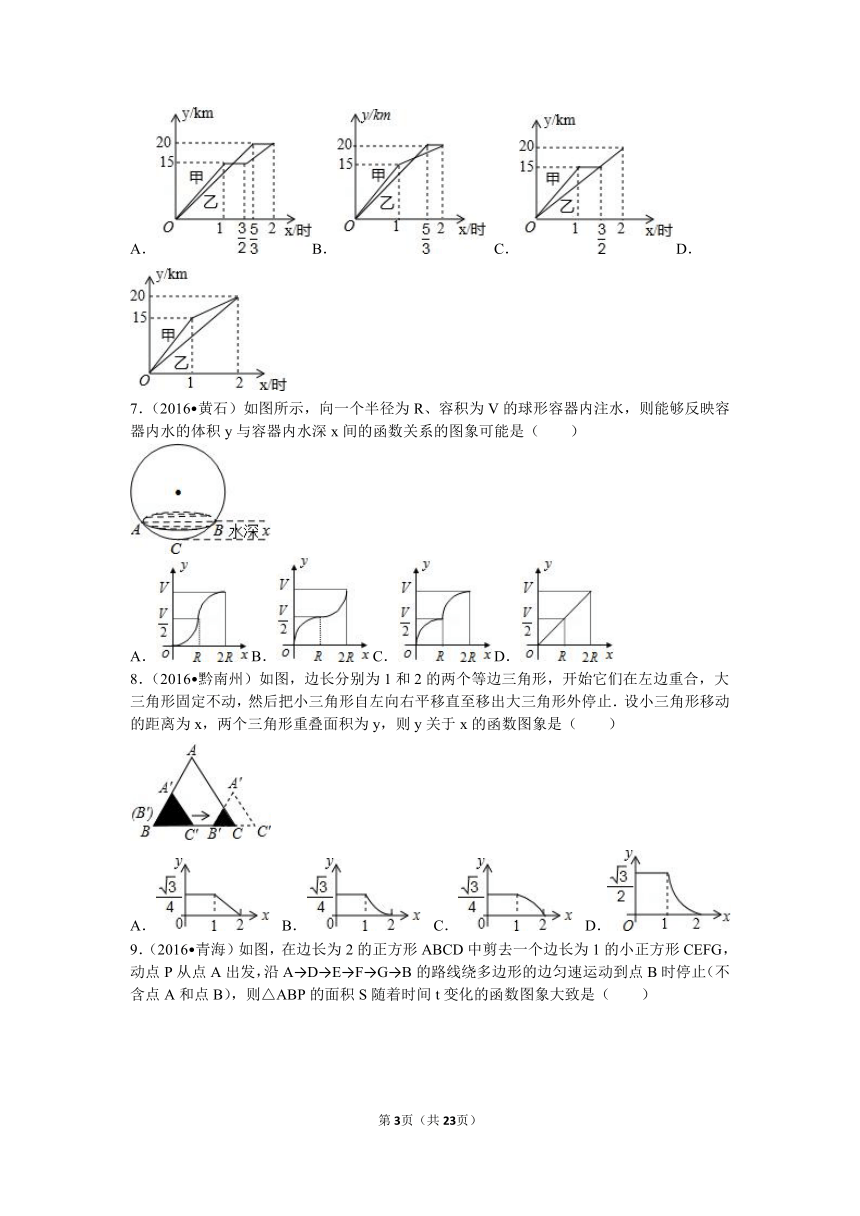
3.(2016 呼伦贝尔)园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A.100m2
B.50m2
C.80m2
D.40m2
4.(2016 新疆)小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )
A.
B.
C.
D.
5.(2016 宜宾)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
6.(2016 安徽)一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.
B.
C.
D.
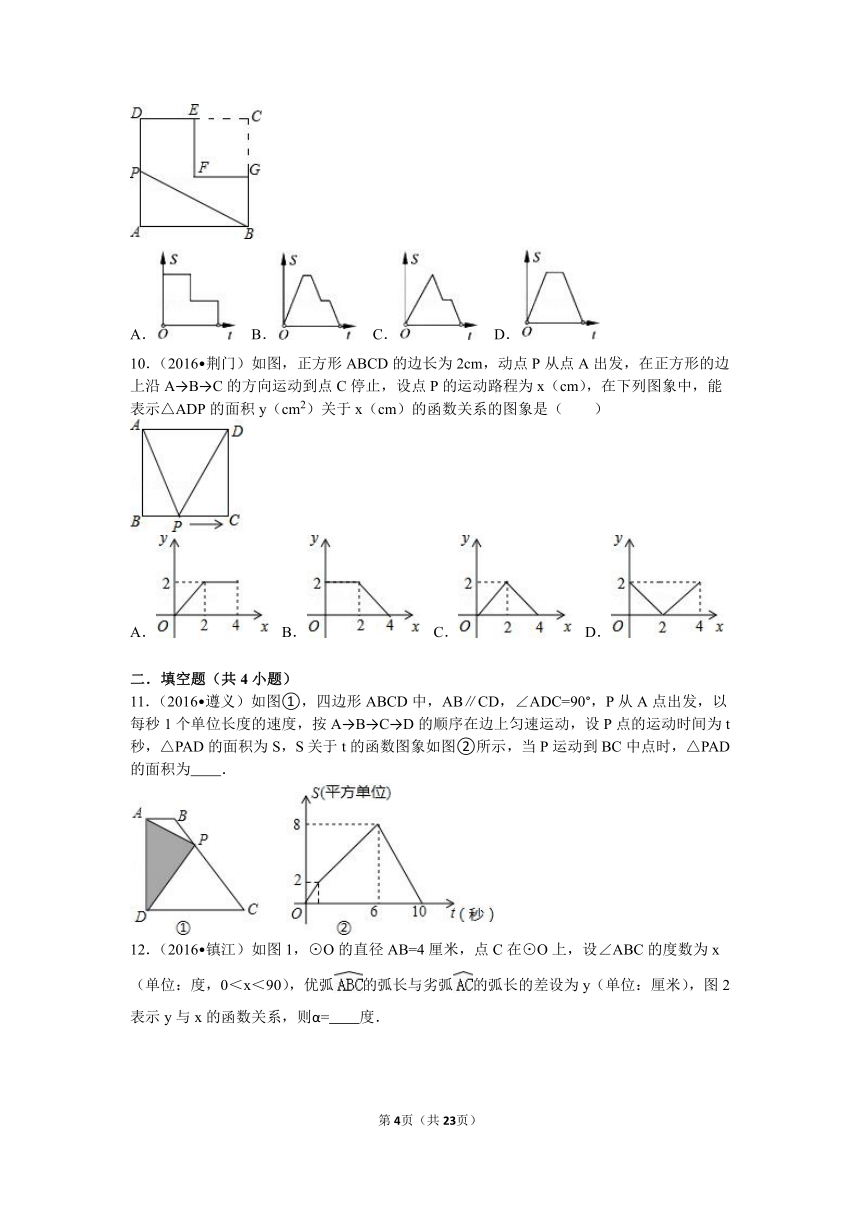
7.(2016 黄石)如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A.
B.
C.
D.
8.(2016 黔南州)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A.
B.
C.
D.
9.(2016 青海)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
B.
C.
D.
10.(2016 荆门)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A.
B.
C.
D.
二.填空题(共4小题)
11.(2016 遵义)如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
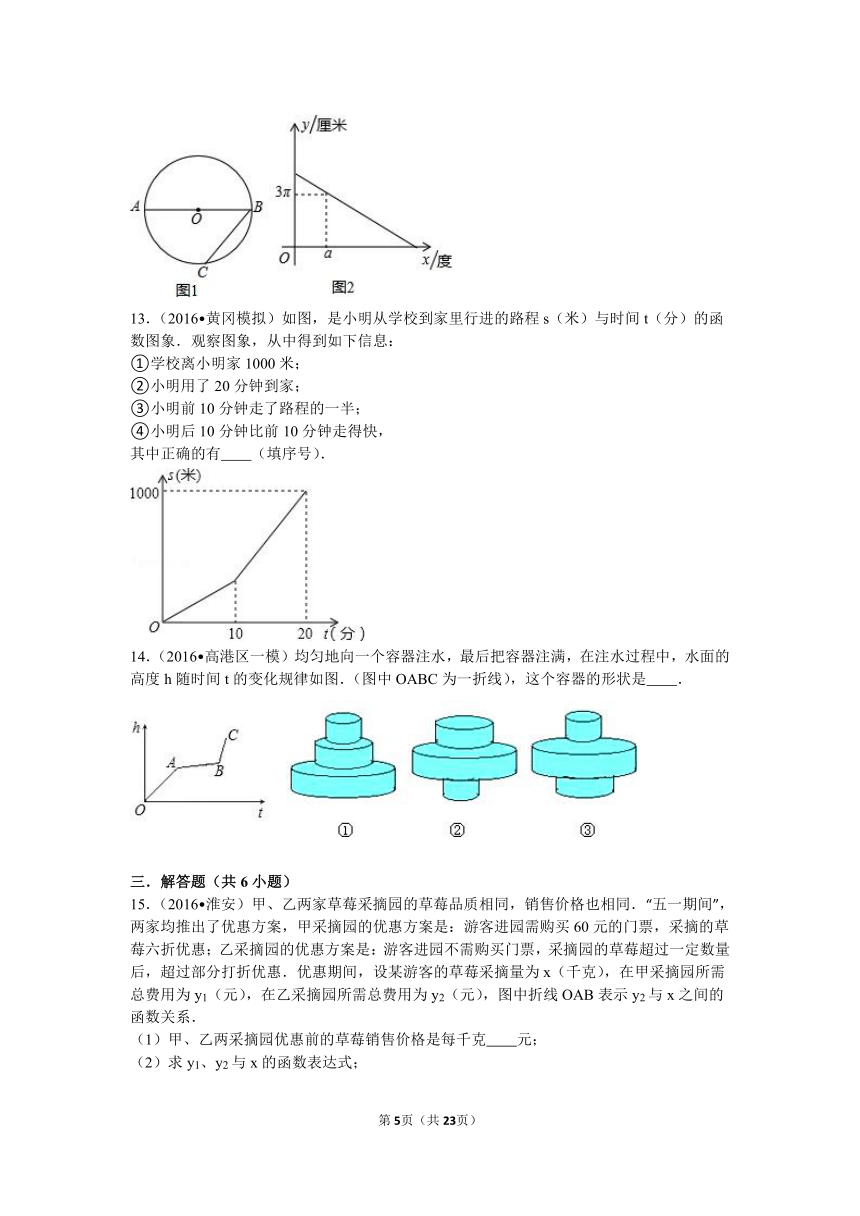
12.(2016 镇江)如图1,⊙O的直径AB=4厘米,点C在⊙O上,设∠ABC的度数为x(单位:度,0<x<90),优弧的弧长与劣弧的弧长的差设为y(单位:厘米),图2表示y与x的函数关系,则α= 度.
13.(2016 黄冈模拟)如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:
①学校离小明家1000米;
②小明用了20分钟到家;
③小明前10分钟走了路程的一半;
④小明后10分钟比前10分钟走得快,
其中正确的有 (填序号).
14.(2016 高港区一模)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 .
三.解答题(共6小题)
15.(2016 淮安)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
16.(2016 大连模拟)如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为 ;
(2)求y关于x的函数关系式,并写出x的取值范围.
17.(2016春 高州市期末)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
18.(2016春 龙岗区期末)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
19.(2016春 永新县期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)
与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
(1)如图反映哪两个变量之间的关系?
(2)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(3)时间10分钟时,洗衣机处于哪个过程?
20.(2016 张家港市二模)如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P、Q运动的速度;
(2)图2中,a= ,b= ,c= ;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
参考答案与试题解析
一.选择题(共10小题)
1.(2016 贵阳)星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A.
B.
C.
D.
【分析】根据给定s关于t的函数图象,分析AB段可得出该段时间蕊蕊妈妈绕以家为圆心的圆弧进行运动,由此即可得出结论.
【解答】解:观察s关于t的函数图象,发现:
在图象AB段,该时间段蕊蕊妈妈离家的距离相等,即绕以家为圆心的圆弧进行运动,
∴可以大致描述蕊蕊妈妈行走的路线是B.
故选B.
【点评】本题考查了函数的图象,解题的关键是分析函数图象的AB段.本题属于基础题,难度不大,解决该题型题目时,根据函数图象分析出大致的运动路径是关键.
2.(2016 衢州)如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.
B.
C.
D.
【分析】由△DEB∽△CMB,得==,求出DE、EB,即可解决问题.
【解答】解:如图,作CM⊥AB于M.
∵CA=CB,AB=30,CM⊥AB,
∴AM=BM=15,CM==20
∵DE⊥BC,
∴∠DEB=∠CMB=90°,
∵∠B=∠B,
∴△DEB∽△CMB,
∴==,
∴==,
∴DE=,EB=,
∴四边形ACED的周长为y=25+(25﹣)++30﹣x=﹣x+80.
∵0<x<30,
∴图象是D.
故选D.
【点评】本题考查函数图象、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是构建函数关系式,注意自变量的取值范围,属于中考常考题型.
3.(2016 呼伦贝尔)园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A.100m2
B.50m2
C.80m2
D.40m2
【分析】根据图象可得,休息后园林队2小时绿化面积为160﹣60=100(m2),然后可得绿化速度.
【解答】解:根据图象可得,休息后园林队2小时绿化面积为160﹣60=100(m2).
每小时绿化面积为100÷2=50(m2).
故选:B.
【点评】此题主要考查了函数图象,关键是正确理解题意,从图象中找出正确信息.
4.(2016 新疆)小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )
A.
B.
C.
D.
【分析】因为在书店里花了10分钟看书,应是一段平行与x轴的线段,B是10分钟,而A是20分钟,依此即可作出判断.
【解答】解:根据题意,从20分钟到30分钟在书店里看书,离家距离没有变化,是一条平行于x轴的线段.
故选B.
【点评】考查了函数的图象,本题是常见的函数题,属于分段函数,前面是正比例函数,中间是平行于x轴的一条线段,后面是一次函数.
5.(2016 宜宾)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
【分析】前4s内,乙的速度﹣时间图象是一条平行于x轴的直线,即速度不变,速度×时间=路程.
甲是一条过原点的直线,则速度均匀增加;
求出两图象的交点坐标,3秒时两速度大小相等,3s前甲的图象在乙的下方,所以3秒前路程不相等;
图象在上方的,说明速度大.
【解答】解:A、根据图象可得,乙前4秒的速度不变,为4米/秒,则行驶的路程为12×4=48米,故A正确;
B、根据图象得:在0到8秒内甲的速度是一条过原点的直线,即甲的速度从0均匀增加到32米/秒,则每秒增加=4米秒/,故B正确;
C、由于甲的图象是过原点的直线,斜率为4,所以可得v=4t(v、t分别表示速度、时间),将v=12m/s代入v=4t得t=3s,则t=3s前,甲的速度小于乙的速度,所以两车到第3秒时行驶的路程不相等,故C错误;
D、在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,故D正确;
由于该题选择错误的,故选C.
【点评】此题考查了函数的图形,通过此类题目的练习,可以培养学生分析问题和运用所学知识解决实际问题的能力,能使学生体会到函数知识的实用性.
6.(2016 安徽)一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.
B.
C.
D.
【分析】分别求出甲乙两人到达C地的时间,再结合已知条件即可解决问题.
【解答】解;由题意,甲走了1小时到了B地,在B地休息了半个小时,2小时正好走到C地,乙走了小时到了C地,在C地休息了小时.
由此可知正确的图象是A.
故选A.
【点评】本题考查函数图象、路程.速度、时间之间的关系,解题的关键是理解题意求出两人到达C地的时间,属于中考常考题型.
7.(2016 黄石)如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A.
B.
C.
D.
【分析】水深h越大,水的体积v就越大,故容器内水的体积y与容器内水深x间的函数是增函数,根据球的特征进行判断分析即可.
【解答】解:根据球形容器形状可知,函数y的变化趋势呈现出,当0<x<R时,y增量越来越大,当R<x<2R时,y增量越来越小,
曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,故y关于x的函数图象是先凹后凸.
故选(A)
【点评】本题主要考查了函数图象的变化特征,解题的关键是利用数形结合的数学思想方法.解得此类试题时注意,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.
8.(2016 黔南州)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A.
B.
C.
D.
【分析】根据题目提供的条件可以求出函数的解析式,根据解析式判断函数的图象的形状.
【解答】解:①x≤1时,两个三角形重叠面积为小三角形的面积,
∴y=×1×=,
②当1<x≤2时,重叠三角形的边长为2﹣x,高为,
y=(2﹣x)×=x2﹣x+,
③当x=2时,两个三角形没有重叠的部分,即重叠面积为0,
故选:B.
【点评】本题主要考查了本题考查了动点问题的函数图象,此类题目的图象往往是几个函数的组合体.
9.(2016 青海)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
B.
C.
D.
【分析】根据点P在AD、DE、EF、FG、GB上时,△ABP的面积S与时间t的关系确定函数图象.
【解答】解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
故选:B.
【点评】本题考查的是动点问题的函数图象,正确分析点P在不同的线段上△ABP的面积S与时间t的关系是解题的关键.
10.(2016 荆门)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A.
B.
C.
D.
【分析】△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.
【解答】解:当P点由A运动到B点时,即0≤x≤2时,y=×2x=x,
当P点由B运动到C点时,即2<x<4时,y=×2×2=2,
符合题意的函数关系的图象是A;
故选:A.
【点评】本题考查了动点函数图象问题,用到的知识点是三角形的面积、一次函数,在图象中应注意自变量的取值范围.
二.填空题(共4小题)
11.(2016 遵义)如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
【分析】由函数图象上的点(6,8)、(10,0)的实际意义可知AB+BC、AB+BC+CD的长及△PAD的最大面积,从而求得AD、CD的长,再根据点P运动到点B时得S△ABD=2,从而求得AB的长,最后根据等腰三角形的中位线定理可求得当P运动到BC中点时,△PAD的面积.
【解答】解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,
∴AD=4,
又∵S△ABD=×AB×AD=2,
∴AB=1,
∴当P点运动到BC中点时,△PAD的面积=×(AB+CD)×AD=5,
故答案为:5.
【点评】本题主要考查动点问题的函数图象,根据函数图象中三角形的面积的变化情况判断出AB、CD、AD的长是解题的关键.
12.(2016 镇江)如图1,⊙O的直径AB=4厘米,点C在⊙O上,设∠ABC的度数为x(单位:度,0<x<90),优弧的弧长与劣弧的弧长的差设为y(单位:厘米),图2表示y与x的函数关系,则α= 度.
【分析】直接利用弧长公式表示出y与x之间的关系,进而代入(a,3π)求出答案.
【解答】解:设∠ABC的度数为x,根据题意可得:
y=﹣
将(a,3π)代入得:
3π=,
解得:α=22.5°.
故答案为:22.5.
【点评】此题主要考查了动点问题的函数图象,正确得出y与x之间的关系式是解题关键.
13.(2016 黄冈模拟)如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:
①学校离小明家1000米;
②小明用了20分钟到家;
③小明前10分钟走了路程的一半;
④小明后10分钟比前10分钟走得快,
其中正确的有 (填序号).
【分析】根据图象的纵坐标,可判断①,根据图象的横坐标,可判断②,根据图象的横坐标、纵坐标,可判断②③.
【解答】解:①由图象的纵坐标可以看出学校离小明家1000米,故①正确;
②由图象的横坐标可以看出小明用了20到家,故②正确;
③由图象的纵横坐标可以看出,小明前10分钟走的路程较少,故③错误;
④由图象的纵横坐标可以看出,小明后10分钟比前10分钟走得快,故④正确;
故答案为:①,②,④.
【点评】本题考查了函数图象,观察函数图象的纵坐标得是解题关键.
14.(2016 高港区一模)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 .
【分析】这是一个用函数来描述事物变化规律的问题,先比较OA、AB、BC三段的变化快慢,再比较三个容器容积的大小,就会把问题解决.
【解答】解:从左面图象可以看出,OA上升较快,AB上升缓慢,BC上升最快.
从右面容器可以看出图①下面容积最大,中间容积较大,上面容积最小.
图②下面容积最小,中间容积最大,上面容积较大.
图③下面容积较大,中间容积最大,上面容积最小.
因为均匀注水,故选③.
【点评】解决这类问题的关键是找清图象描述与实际问题的一一对应关系.
三.解答题(共6小题)
15.(2016 淮安)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
【分析】(1)根据单价=,即可解决问题.
(2)y1函数表达式=60+单价×数量,y2与x的函数表达式结合图象利用待定系数法即可解决.
(3)画出函数图象后y1在y2下面即可解决问题.
【解答】解:(1)甲、乙两采摘园优惠前的草莓销售价格是每千克=30元.
故答案为:30.
(2)由题意y1=30×0.6x+60=18x+60,
由图可得,当0≤x≤10时,y2=30x;
当x>10时,设y2=kx+b,
将(10,300)和(20,450)代入y2=kx+b,
解得y2=15x+150,
所以y2=,
(3)函数y1的图象如图所示,
由解得,所以点F坐标(5,150),
由解得,所以点E坐标(30,600).
由图象可知甲采摘园所需总费用较少时5<x<30.
【点评】本题考查分段函数、一次函数,单价、数量、总价之间的关系,解题的关键是熟练掌握待定系数法,学会利用图象确定自变量取值范围,属于中考常考题型.
16.(2016 大连模拟)如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为 ;
(2)求y关于x的函数关系式,并写出x的取值范围.
【分析】(1)通过图2观察可知y=0时x=4,即D点从B运动到C平移的距离为4;
(2)当△DEF在平移过程中,与△ABC的重合部分有三种情况,将三种图形分别画出,通过作辅助线构造相似三角形,通过相似三角形对应边的关系,将各边用x表示出来,即可以列出y与x的函数关系式.
【解答】解:(1)由图2得当x=4时,y=0,说明此时△DEF与△ABC无重合部分,
则点D从B到C运动的距离为4,即BC=4;
故答案为:4.
(2)当DE经过点A时(如图1),BD=5,CD=1,
∵△ABC≌△DEF.
∴∠EDF=∠BAC.
∵∠ACD=∠BCA
∴△ADC∽△BAC.
∴,即.AC=2
∴n=2
当0≤x≤2时(如图2),
设ED、EF与AB分别相交于点M,G,作MN⊥BC,垂足为N.
则∠MNB=90°=∠EFD=∠C.
∵∠MDN=∠EDF.
∴△DMN∽△DEF.
∴,即.
∴MN=2DN.
设DN=n,则MN=2n.
同理△BMN∽△BAC.
∴.即,
∴BN=4n,即x+n=4n.
∴n=x.
∴S△BDM= BD MN=2
同理△BGF∽△BAC
∴,即.
∴GF=,
∴y=S△BGF﹣S△BDM=2=﹣x2+x+1.
当2<x≤3时(如图3),
由①知,S△BDM=x2.
∴y=S△ABC﹣S△BDM=2=﹣x2+4
当3<x≤4时(如图4),
设DE与AB相交于点H.
同理△DHC∽△DEF.
∴,即
∴HC=24﹣x.
∴y==x2﹣8x+16
∴y=.
【点评】本题考查了平移的性质、相似三角形性质,解题的关键是要找到△DEF运动过程中与△ABC重叠面积的不同情况,通过辅助线构造相似三角形,要注意分类讨论画出对应的图象.
17.(2016春 高州市期末)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
【分析】(1)根据图象,观察学校与小明家的纵坐标,可得答案;
(2)分析图象,找函数变化最快的一段,可得小明骑车速度最快的时间段,进而可得其速度;
(3)读图,对应题意找到其在书店停留的时间段,进而可得其在书店停留的时间;
(4)读图,计算可得答案,注意要计算路程.
【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据图象,12≤x≤14时,直线最陡,
故小明在12﹣14分钟最快,速度为=450米/分.
(3)根据题意,小明在书店停留的时间为从8分到12分,
故小明在书店停留了4分钟.
(4)读图可得:小明共行驶了1200+600+900=2700米,共用了14分钟.
【点评】本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
18.(2016春 龙岗区期末)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
【分析】(1)根据函数图象的横坐标,可得答案;根据函数图象的纵坐标,可得加油量;
(2)根据待定系数法,可得函数解析式;
(3)根据单位耗油量乘以行驶时间,可得行驶路程,根据有理数的大小比较,可得答案.
【解答】解:(1)由横坐标看出,5小时后加油,由纵坐标看出,加了36﹣12=24(L)油
(2)设解析式为Q=kt+b,将(0,42),(5,12)代入函数解析式,得
,
解得.
故函数解析式为Q=42﹣6t
(3)够用,理由如下
单位耗油量为=6,
6×40﹣230=240﹣230=10>0,
还可以在行驶10千米,
故油够用.
【点评】本题考查了函数图象,观察函数图象的横坐标得出时间,观察函数图象的纵坐标得出剩余油量是解题关键,利用待定系数法求函数解析式.
19.(2016春 永新县期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)
与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
(1)如图反映哪两个变量之间的关系?
(2)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(3)时间10分钟时,洗衣机处于哪个过程?
【分析】(1)根据函数图象可判断,这是水量与时间之间的关系;
(2)结合函数图象可得进水时间是4分钟,清洗时洗衣机的水量是40升;
(3)0﹣4分钟是进水过程,4﹣15分钟是清洗过程,15分钟过后是排水过程.
【解答】解:(1)图象反应的是:水量与时间之间的关系;
(2)洗衣机的进水时间是4分钟,清洗时洗衣机中的水量40升;
(3)0﹣4分钟是进水过程,4﹣15分钟是清洗过程,15分钟过后是排水过程,
故可得时间10分钟时,洗衣机处于清洗过程.
【点评】本题考查了函数的图象,要求结合实际情况理解图象各个点的实际意义.
20.(2016 张家港市二模)如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P、Q运动的速度;
(2)图2中,a= ,b= ,c= ;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
【分析】(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,根据图象可知经过2秒两点之间的距离为0,即经过2秒两点相遇.根据相遇时,两点运动的路程之和=12厘米列出方程,求解即可;
(2)根据图象可知,a的值为动点Q从点B运动到点A的时间,根据时间=路程÷速度列式求出a=3;b的值为动点P运动3秒时的路程,根据路程=速度×时间列式求解;c的值为动点P从点A运动到点B的时间,根据时间=路程÷速度列式求解;
(3)当3≤t≤6时,设s与t之间的函数关系式为s=kt+b,将(3,6),(6,12)代入,利用待定系数法即可求解.
【解答】解:(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,
根据题意,得2(x+2x)=12,
解得x=2.
答:动点P、Q运动的速度分别是2厘米/秒、4厘米/秒;
(2)动点Q运动的时间a==3;
经过3秒,动点Q从点B运动到点A,此时动点P运动的路程为2×3=6,即b=6;
动点P运动的时间c==6;
故答案为3,6,6;
(3)当3≤t≤6时,设s与t之间的函数关系式为s=kt+b,
∵图象过点(3,6),(6,12),
∴,
解得,
∴s与t之间的函数关系式为s=2t(3≤t≤6).
【点评】本题考查了动点问题的函数图象,路程、速度与时间的关系,待定系数法求一次函数的解析式等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
第1页(共1页)
测
试
卷
一.选择题(共10小题)
1.(2016 贵阳)星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A.
B.
C.
D.
2.(2016 衢州)如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.
B.
C.
D.
3.(2016 呼伦贝尔)园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A.100m2
B.50m2
C.80m2
D.40m2
4.(2016 新疆)小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )
A.
B.
C.
D.
5.(2016 宜宾)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
6.(2016 安徽)一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.
B.
C.
D.
7.(2016 黄石)如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A.
B.
C.
D.
8.(2016 黔南州)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A.
B.
C.
D.
9.(2016 青海)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
B.
C.
D.
10.(2016 荆门)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A.
B.
C.
D.
二.填空题(共4小题)
11.(2016 遵义)如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
12.(2016 镇江)如图1,⊙O的直径AB=4厘米,点C在⊙O上,设∠ABC的度数为x(单位:度,0<x<90),优弧的弧长与劣弧的弧长的差设为y(单位:厘米),图2表示y与x的函数关系,则α= 度.
13.(2016 黄冈模拟)如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:
①学校离小明家1000米;
②小明用了20分钟到家;
③小明前10分钟走了路程的一半;
④小明后10分钟比前10分钟走得快,
其中正确的有 (填序号).
14.(2016 高港区一模)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 .
三.解答题(共6小题)
15.(2016 淮安)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
16.(2016 大连模拟)如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为 ;
(2)求y关于x的函数关系式,并写出x的取值范围.
17.(2016春 高州市期末)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
18.(2016春 龙岗区期末)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
19.(2016春 永新县期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)
与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
(1)如图反映哪两个变量之间的关系?
(2)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(3)时间10分钟时,洗衣机处于哪个过程?
20.(2016 张家港市二模)如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P、Q运动的速度;
(2)图2中,a= ,b= ,c= ;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
参考答案与试题解析
一.选择题(共10小题)
1.(2016 贵阳)星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A.
B.
C.
D.
【分析】根据给定s关于t的函数图象,分析AB段可得出该段时间蕊蕊妈妈绕以家为圆心的圆弧进行运动,由此即可得出结论.
【解答】解:观察s关于t的函数图象,发现:
在图象AB段,该时间段蕊蕊妈妈离家的距离相等,即绕以家为圆心的圆弧进行运动,
∴可以大致描述蕊蕊妈妈行走的路线是B.
故选B.
【点评】本题考查了函数的图象,解题的关键是分析函数图象的AB段.本题属于基础题,难度不大,解决该题型题目时,根据函数图象分析出大致的运动路径是关键.
2.(2016 衢州)如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.
B.
C.
D.
【分析】由△DEB∽△CMB,得==,求出DE、EB,即可解决问题.
【解答】解:如图,作CM⊥AB于M.
∵CA=CB,AB=30,CM⊥AB,
∴AM=BM=15,CM==20
∵DE⊥BC,
∴∠DEB=∠CMB=90°,
∵∠B=∠B,
∴△DEB∽△CMB,
∴==,
∴==,
∴DE=,EB=,
∴四边形ACED的周长为y=25+(25﹣)++30﹣x=﹣x+80.
∵0<x<30,
∴图象是D.
故选D.
【点评】本题考查函数图象、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是构建函数关系式,注意自变量的取值范围,属于中考常考题型.
3.(2016 呼伦贝尔)园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A.100m2
B.50m2
C.80m2
D.40m2
【分析】根据图象可得,休息后园林队2小时绿化面积为160﹣60=100(m2),然后可得绿化速度.
【解答】解:根据图象可得,休息后园林队2小时绿化面积为160﹣60=100(m2).
每小时绿化面积为100÷2=50(m2).
故选:B.
【点评】此题主要考查了函数图象,关键是正确理解题意,从图象中找出正确信息.
4.(2016 新疆)小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )
A.
B.
C.
D.
【分析】因为在书店里花了10分钟看书,应是一段平行与x轴的线段,B是10分钟,而A是20分钟,依此即可作出判断.
【解答】解:根据题意,从20分钟到30分钟在书店里看书,离家距离没有变化,是一条平行于x轴的线段.
故选B.
【点评】考查了函数的图象,本题是常见的函数题,属于分段函数,前面是正比例函数,中间是平行于x轴的一条线段,后面是一次函数.
5.(2016 宜宾)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
【分析】前4s内,乙的速度﹣时间图象是一条平行于x轴的直线,即速度不变,速度×时间=路程.
甲是一条过原点的直线,则速度均匀增加;
求出两图象的交点坐标,3秒时两速度大小相等,3s前甲的图象在乙的下方,所以3秒前路程不相等;
图象在上方的,说明速度大.
【解答】解:A、根据图象可得,乙前4秒的速度不变,为4米/秒,则行驶的路程为12×4=48米,故A正确;
B、根据图象得:在0到8秒内甲的速度是一条过原点的直线,即甲的速度从0均匀增加到32米/秒,则每秒增加=4米秒/,故B正确;
C、由于甲的图象是过原点的直线,斜率为4,所以可得v=4t(v、t分别表示速度、时间),将v=12m/s代入v=4t得t=3s,则t=3s前,甲的速度小于乙的速度,所以两车到第3秒时行驶的路程不相等,故C错误;
D、在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,故D正确;
由于该题选择错误的,故选C.
【点评】此题考查了函数的图形,通过此类题目的练习,可以培养学生分析问题和运用所学知识解决实际问题的能力,能使学生体会到函数知识的实用性.
6.(2016 安徽)一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.
B.
C.
D.
【分析】分别求出甲乙两人到达C地的时间,再结合已知条件即可解决问题.
【解答】解;由题意,甲走了1小时到了B地,在B地休息了半个小时,2小时正好走到C地,乙走了小时到了C地,在C地休息了小时.
由此可知正确的图象是A.
故选A.
【点评】本题考查函数图象、路程.速度、时间之间的关系,解题的关键是理解题意求出两人到达C地的时间,属于中考常考题型.
7.(2016 黄石)如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A.
B.
C.
D.
【分析】水深h越大,水的体积v就越大,故容器内水的体积y与容器内水深x间的函数是增函数,根据球的特征进行判断分析即可.
【解答】解:根据球形容器形状可知,函数y的变化趋势呈现出,当0<x<R时,y增量越来越大,当R<x<2R时,y增量越来越小,
曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,故y关于x的函数图象是先凹后凸.
故选(A)
【点评】本题主要考查了函数图象的变化特征,解题的关键是利用数形结合的数学思想方法.解得此类试题时注意,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.
8.(2016 黔南州)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A.
B.
C.
D.
【分析】根据题目提供的条件可以求出函数的解析式,根据解析式判断函数的图象的形状.
【解答】解:①x≤1时,两个三角形重叠面积为小三角形的面积,
∴y=×1×=,
②当1<x≤2时,重叠三角形的边长为2﹣x,高为,
y=(2﹣x)×=x2﹣x+,
③当x=2时,两个三角形没有重叠的部分,即重叠面积为0,
故选:B.
【点评】本题主要考查了本题考查了动点问题的函数图象,此类题目的图象往往是几个函数的组合体.
9.(2016 青海)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
B.
C.
D.
【分析】根据点P在AD、DE、EF、FG、GB上时,△ABP的面积S与时间t的关系确定函数图象.
【解答】解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
故选:B.
【点评】本题考查的是动点问题的函数图象,正确分析点P在不同的线段上△ABP的面积S与时间t的关系是解题的关键.
10.(2016 荆门)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A.
B.
C.
D.
【分析】△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.
【解答】解:当P点由A运动到B点时,即0≤x≤2时,y=×2x=x,
当P点由B运动到C点时,即2<x<4时,y=×2×2=2,
符合题意的函数关系的图象是A;
故选:A.
【点评】本题考查了动点函数图象问题,用到的知识点是三角形的面积、一次函数,在图象中应注意自变量的取值范围.
二.填空题(共4小题)
11.(2016 遵义)如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
【分析】由函数图象上的点(6,8)、(10,0)的实际意义可知AB+BC、AB+BC+CD的长及△PAD的最大面积,从而求得AD、CD的长,再根据点P运动到点B时得S△ABD=2,从而求得AB的长,最后根据等腰三角形的中位线定理可求得当P运动到BC中点时,△PAD的面积.
【解答】解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,
∴AD=4,
又∵S△ABD=×AB×AD=2,
∴AB=1,
∴当P点运动到BC中点时,△PAD的面积=×(AB+CD)×AD=5,
故答案为:5.
【点评】本题主要考查动点问题的函数图象,根据函数图象中三角形的面积的变化情况判断出AB、CD、AD的长是解题的关键.
12.(2016 镇江)如图1,⊙O的直径AB=4厘米,点C在⊙O上,设∠ABC的度数为x(单位:度,0<x<90),优弧的弧长与劣弧的弧长的差设为y(单位:厘米),图2表示y与x的函数关系,则α= 度.
【分析】直接利用弧长公式表示出y与x之间的关系,进而代入(a,3π)求出答案.
【解答】解:设∠ABC的度数为x,根据题意可得:
y=﹣
将(a,3π)代入得:
3π=,
解得:α=22.5°.
故答案为:22.5.
【点评】此题主要考查了动点问题的函数图象,正确得出y与x之间的关系式是解题关键.
13.(2016 黄冈模拟)如图,是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:
①学校离小明家1000米;
②小明用了20分钟到家;
③小明前10分钟走了路程的一半;
④小明后10分钟比前10分钟走得快,
其中正确的有 (填序号).
【分析】根据图象的纵坐标,可判断①,根据图象的横坐标,可判断②,根据图象的横坐标、纵坐标,可判断②③.
【解答】解:①由图象的纵坐标可以看出学校离小明家1000米,故①正确;
②由图象的横坐标可以看出小明用了20到家,故②正确;
③由图象的纵横坐标可以看出,小明前10分钟走的路程较少,故③错误;
④由图象的纵横坐标可以看出,小明后10分钟比前10分钟走得快,故④正确;
故答案为:①,②,④.
【点评】本题考查了函数图象,观察函数图象的纵坐标得是解题关键.
14.(2016 高港区一模)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 .
【分析】这是一个用函数来描述事物变化规律的问题,先比较OA、AB、BC三段的变化快慢,再比较三个容器容积的大小,就会把问题解决.
【解答】解:从左面图象可以看出,OA上升较快,AB上升缓慢,BC上升最快.
从右面容器可以看出图①下面容积最大,中间容积较大,上面容积最小.
图②下面容积最小,中间容积最大,上面容积较大.
图③下面容积较大,中间容积最大,上面容积最小.
因为均匀注水,故选③.
【点评】解决这类问题的关键是找清图象描述与实际问题的一一对应关系.
三.解答题(共6小题)
15.(2016 淮安)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
【分析】(1)根据单价=,即可解决问题.
(2)y1函数表达式=60+单价×数量,y2与x的函数表达式结合图象利用待定系数法即可解决.
(3)画出函数图象后y1在y2下面即可解决问题.
【解答】解:(1)甲、乙两采摘园优惠前的草莓销售价格是每千克=30元.
故答案为:30.
(2)由题意y1=30×0.6x+60=18x+60,
由图可得,当0≤x≤10时,y2=30x;
当x>10时,设y2=kx+b,
将(10,300)和(20,450)代入y2=kx+b,
解得y2=15x+150,
所以y2=,
(3)函数y1的图象如图所示,
由解得,所以点F坐标(5,150),
由解得,所以点E坐标(30,600).
由图象可知甲采摘园所需总费用较少时5<x<30.
【点评】本题考查分段函数、一次函数,单价、数量、总价之间的关系,解题的关键是熟练掌握待定系数法,学会利用图象确定自变量取值范围,属于中考常考题型.
16.(2016 大连模拟)如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为 ;
(2)求y关于x的函数关系式,并写出x的取值范围.
【分析】(1)通过图2观察可知y=0时x=4,即D点从B运动到C平移的距离为4;
(2)当△DEF在平移过程中,与△ABC的重合部分有三种情况,将三种图形分别画出,通过作辅助线构造相似三角形,通过相似三角形对应边的关系,将各边用x表示出来,即可以列出y与x的函数关系式.
【解答】解:(1)由图2得当x=4时,y=0,说明此时△DEF与△ABC无重合部分,
则点D从B到C运动的距离为4,即BC=4;
故答案为:4.
(2)当DE经过点A时(如图1),BD=5,CD=1,
∵△ABC≌△DEF.
∴∠EDF=∠BAC.
∵∠ACD=∠BCA
∴△ADC∽△BAC.
∴,即.AC=2
∴n=2
当0≤x≤2时(如图2),
设ED、EF与AB分别相交于点M,G,作MN⊥BC,垂足为N.
则∠MNB=90°=∠EFD=∠C.
∵∠MDN=∠EDF.
∴△DMN∽△DEF.
∴,即.
∴MN=2DN.
设DN=n,则MN=2n.
同理△BMN∽△BAC.
∴.即,
∴BN=4n,即x+n=4n.
∴n=x.
∴S△BDM= BD MN=2
同理△BGF∽△BAC
∴,即.
∴GF=,
∴y=S△BGF﹣S△BDM=2=﹣x2+x+1.
当2<x≤3时(如图3),
由①知,S△BDM=x2.
∴y=S△ABC﹣S△BDM=2=﹣x2+4
当3<x≤4时(如图4),
设DE与AB相交于点H.
同理△DHC∽△DEF.
∴,即
∴HC=24﹣x.
∴y==x2﹣8x+16
∴y=.
【点评】本题考查了平移的性质、相似三角形性质,解题的关键是要找到△DEF运动过程中与△ABC重叠面积的不同情况,通过辅助线构造相似三角形,要注意分类讨论画出对应的图象.
17.(2016春 高州市期末)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
【分析】(1)根据图象,观察学校与小明家的纵坐标,可得答案;
(2)分析图象,找函数变化最快的一段,可得小明骑车速度最快的时间段,进而可得其速度;
(3)读图,对应题意找到其在书店停留的时间段,进而可得其在书店停留的时间;
(4)读图,计算可得答案,注意要计算路程.
【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据图象,12≤x≤14时,直线最陡,
故小明在12﹣14分钟最快,速度为=450米/分.
(3)根据题意,小明在书店停留的时间为从8分到12分,
故小明在书店停留了4分钟.
(4)读图可得:小明共行驶了1200+600+900=2700米,共用了14分钟.
【点评】本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
18.(2016春 龙岗区期末)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
【分析】(1)根据函数图象的横坐标,可得答案;根据函数图象的纵坐标,可得加油量;
(2)根据待定系数法,可得函数解析式;
(3)根据单位耗油量乘以行驶时间,可得行驶路程,根据有理数的大小比较,可得答案.
【解答】解:(1)由横坐标看出,5小时后加油,由纵坐标看出,加了36﹣12=24(L)油
(2)设解析式为Q=kt+b,将(0,42),(5,12)代入函数解析式,得
,
解得.
故函数解析式为Q=42﹣6t
(3)够用,理由如下
单位耗油量为=6,
6×40﹣230=240﹣230=10>0,
还可以在行驶10千米,
故油够用.
【点评】本题考查了函数图象,观察函数图象的横坐标得出时间,观察函数图象的纵坐标得出剩余油量是解题关键,利用待定系数法求函数解析式.
19.(2016春 永新县期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)
与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
(1)如图反映哪两个变量之间的关系?
(2)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(3)时间10分钟时,洗衣机处于哪个过程?
【分析】(1)根据函数图象可判断,这是水量与时间之间的关系;
(2)结合函数图象可得进水时间是4分钟,清洗时洗衣机的水量是40升;
(3)0﹣4分钟是进水过程,4﹣15分钟是清洗过程,15分钟过后是排水过程.
【解答】解:(1)图象反应的是:水量与时间之间的关系;
(2)洗衣机的进水时间是4分钟,清洗时洗衣机中的水量40升;
(3)0﹣4分钟是进水过程,4﹣15分钟是清洗过程,15分钟过后是排水过程,
故可得时间10分钟时,洗衣机处于清洗过程.
【点评】本题考查了函数的图象,要求结合实际情况理解图象各个点的实际意义.
20.(2016 张家港市二模)如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P、Q运动的速度;
(2)图2中,a= ,b= ,c= ;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
【分析】(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,根据图象可知经过2秒两点之间的距离为0,即经过2秒两点相遇.根据相遇时,两点运动的路程之和=12厘米列出方程,求解即可;
(2)根据图象可知,a的值为动点Q从点B运动到点A的时间,根据时间=路程÷速度列式求出a=3;b的值为动点P运动3秒时的路程,根据路程=速度×时间列式求解;c的值为动点P从点A运动到点B的时间,根据时间=路程÷速度列式求解;
(3)当3≤t≤6时,设s与t之间的函数关系式为s=kt+b,将(3,6),(6,12)代入,利用待定系数法即可求解.
【解答】解:(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,
根据题意,得2(x+2x)=12,
解得x=2.
答:动点P、Q运动的速度分别是2厘米/秒、4厘米/秒;
(2)动点Q运动的时间a==3;
经过3秒,动点Q从点B运动到点A,此时动点P运动的路程为2×3=6,即b=6;
动点P运动的时间c==6;
故答案为3,6,6;
(3)当3≤t≤6时,设s与t之间的函数关系式为s=kt+b,
∵图象过点(3,6),(6,12),
∴,
解得,
∴s与t之间的函数关系式为s=2t(3≤t≤6).
【点评】本题考查了动点问题的函数图象,路程、速度与时间的关系,待定系数法求一次函数的解析式等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
第1页(共1页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
