3.1.2 复数的概念
图片预览



文档简介
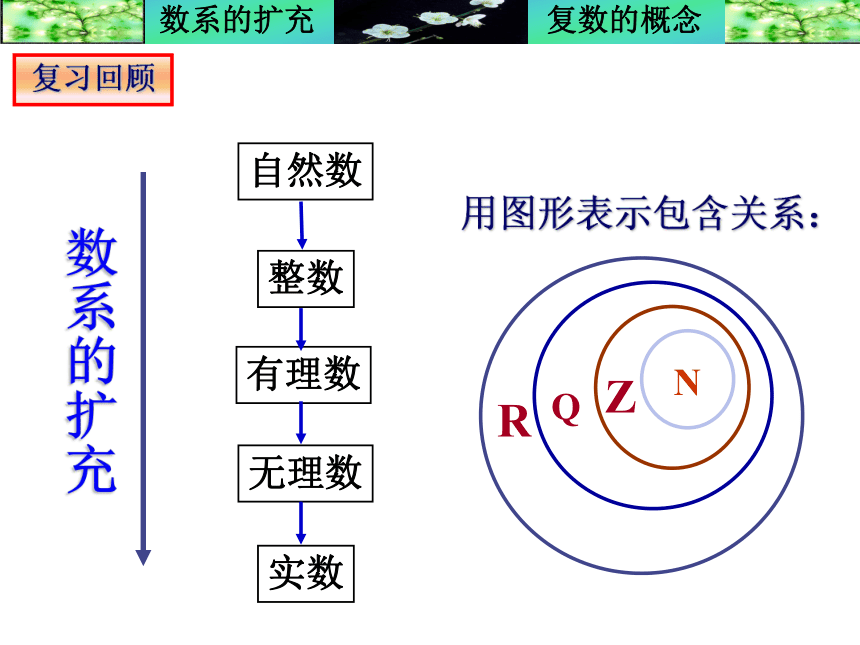
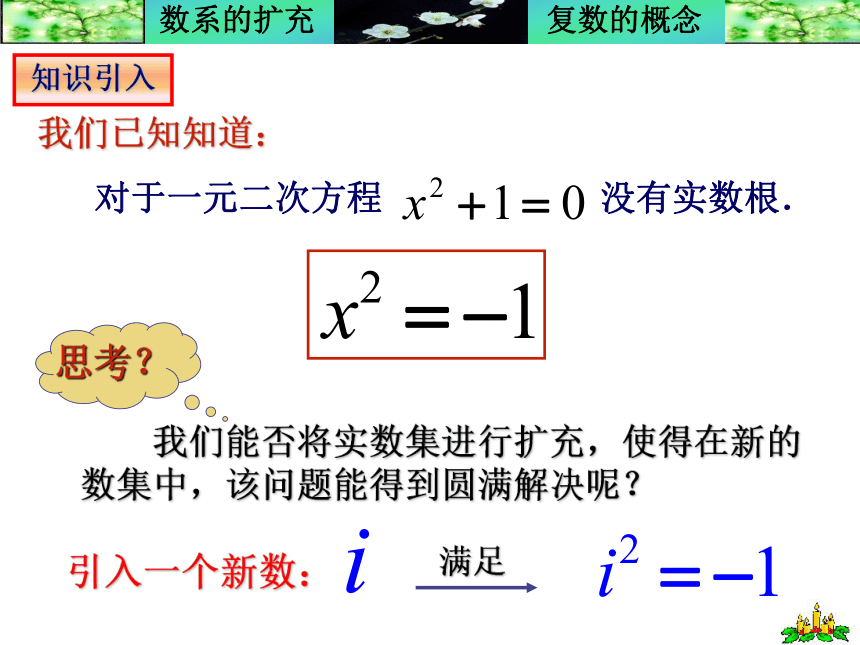
课件13张PPT。3.1.2 复数的概念数系的扩充用图形表示包含关系:复习回顾知识引入引入一个新数: 现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集,
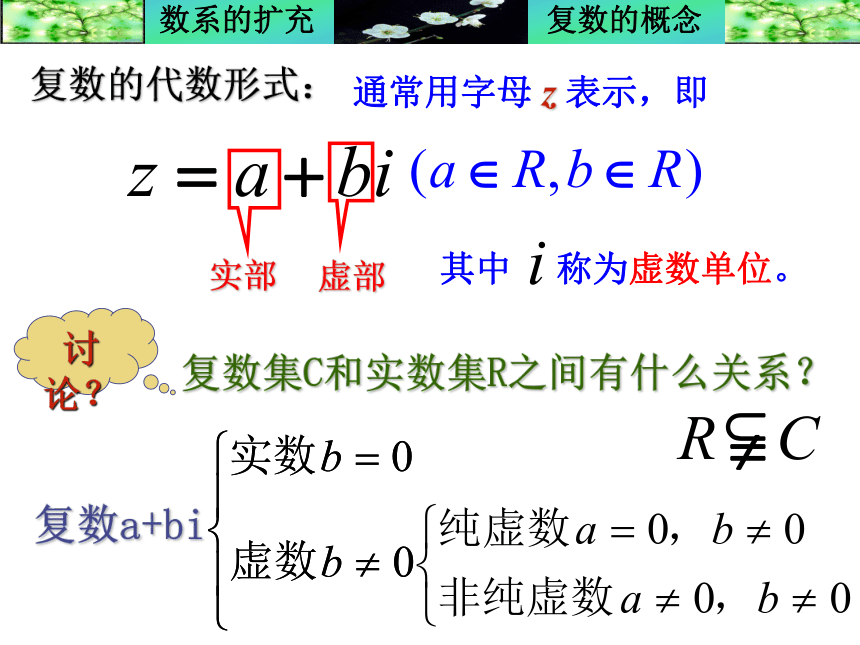
一般用字母C表示 .一般的三次方程可化为一个一次方程和一个二次方程复系数的一元n次方程在复数范围内恰有n个根复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。复数a+bi练一练:1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。5 +8,02、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z= a一定不是虚数例1 实数m取什么值时,复数
是(1)实数? (2)虚数? (3)纯虚数?解: (1)当 ,即 时,复数z 是实数.(2)当 ,即 时,复数z 是虚数.(3)当即 时,复数z 是
纯虚数.练习:当m为何实数时,复数
是 (1)实数 (2)虚数 (3)纯虚数 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.例2 已知 ,其中 求解:根据复数相等的定义,得方程组解得 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.特别注意:实数的有些结论在复数集中不成立(象平面几何的有些结论在立体几何中不成立一样)(1)两实数可以比较大小,但两复数不一定
两复数中只要有一个不是实数就不能比较大小(2)在实数中a2≥0,在复数中不一定(i2=-1)(3)在实数中a2+b2=0,则a=b=0
在复数中不一定(i2+12=0,但i、1都不为0)
小结:1.虚数单位i的引入;注意:a,b,c,d∈R,否则不能左推计算:1-1B
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集,
一般用字母C表示 .一般的三次方程可化为一个一次方程和一个二次方程复系数的一元n次方程在复数范围内恰有n个根复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。复数a+bi练一练:1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。5 +8,02、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z= a一定不是虚数例1 实数m取什么值时,复数
是(1)实数? (2)虚数? (3)纯虚数?解: (1)当 ,即 时,复数z 是实数.(2)当 ,即 时,复数z 是虚数.(3)当即 时,复数z 是
纯虚数.练习:当m为何实数时,复数
是 (1)实数 (2)虚数 (3)纯虚数 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.例2 已知 ,其中 求解:根据复数相等的定义,得方程组解得 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.特别注意:实数的有些结论在复数集中不成立(象平面几何的有些结论在立体几何中不成立一样)(1)两实数可以比较大小,但两复数不一定
两复数中只要有一个不是实数就不能比较大小(2)在实数中a2≥0,在复数中不一定(i2=-1)(3)在实数中a2+b2=0,则a=b=0
在复数中不一定(i2+12=0,但i、1都不为0)
小结:1.虚数单位i的引入;注意:a,b,c,d∈R,否则不能左推计算:1-1B
