湖南省怀化市2010年高中学业水平模拟测试
文档属性
| 名称 | 湖南省怀化市2010年高中学业水平模拟测试 |  | |
| 格式 | zip | ||
| 文件大小 | 177.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-23 07:33:00 | ||
图片预览


文档简介
2010年怀化市高中学业水平模拟测试
数 学
命题:怀化市铁路第一中学 向重新 审题 怀化市教科院 唐振球 张理科
时量120分钟,满分100分.
一、选择题:本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则
A. B. C. D.
2.直线l经过点且与直线垂直,则l的方程是
A. B.
C. D.
3.将如图所示的转盘分成五个面积相等的区域,规定:某人随
机转动转盘,当静止时,若指针指向N区域则中奖. 按此规
则,此人中奖的概率是
A. B. C. D.
4.下列函数在定义域中是减函数的是
A. B. C. D.
5.已知平面向量 ,且,则
A.3 B.9 C. D.
6.下面三视图表示的几何体是
A.六棱柱 B.六棱锥 C.六棱台 D.平行六面体
7.将的图象向左平移个单位,所得图象的函数解析式为
A. B.
C. D.
8.函数的零点所在的区间大致是
A.(1.2) B.(2.3) C.(3.4) D.(4.5)
9.圆心坐标是,半径等于的圆的方程是
A. B.
C. D.
10.已知,,,则,,的大小顺序为
A. B. C. D.
二、填空题:本大题共5小题,每小题4分,满分20分.
11.已知函数, 若, 则____________.
12.在平面直角坐标系中,不等式组所围成的平面区域的面积
为_________________.
13.把89化成五进制数结果为_________________.
14.在中,A, B, C所对的边分别为a, b, c, 若
,则________, = .
15.按如右程序框图运行程序,则输出的S= .
三、解答题:本大题共5小题,满分40分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)
已知,.
(1)求的值;
(2)求的周期和单调递增区间.
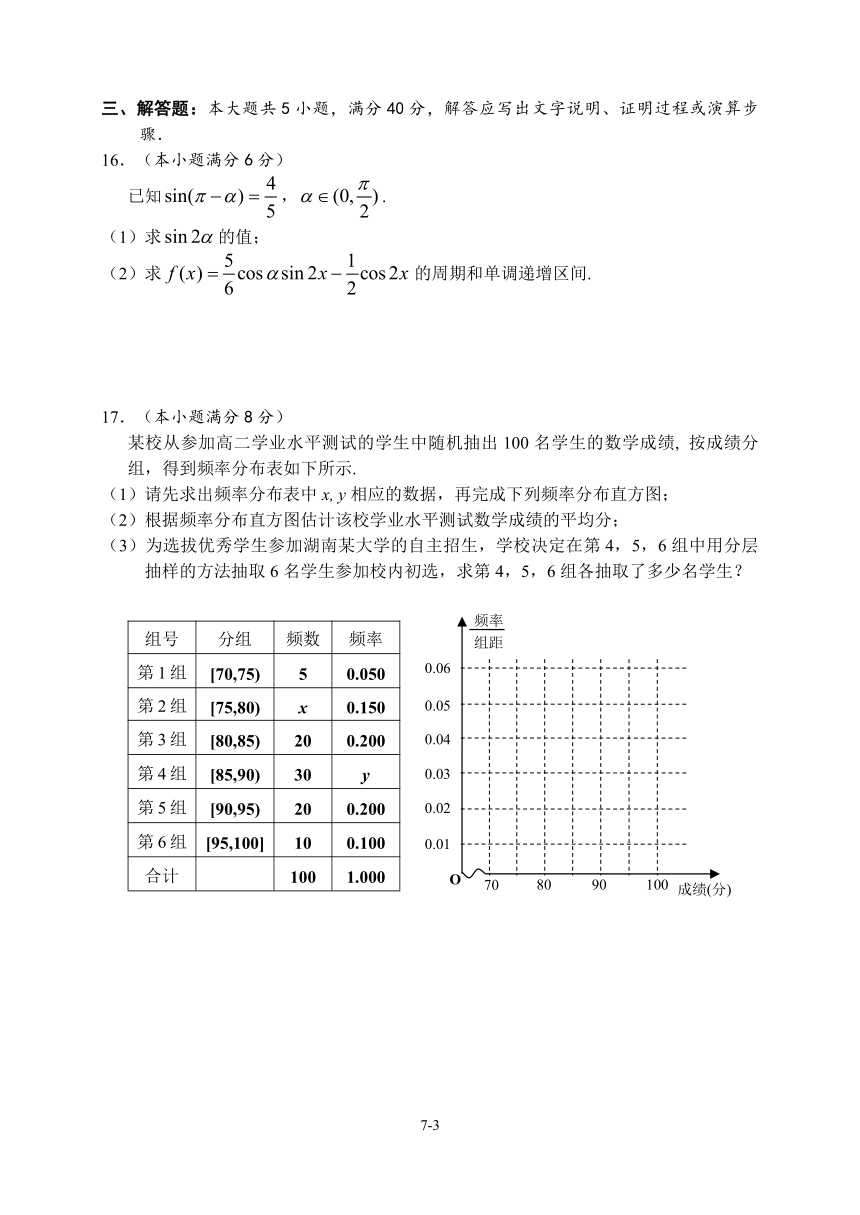
17.(本小题满分8分)
某校从参加高二学业水平测试的学生中随机抽出100名学生的数学成绩, 按成绩分组,得到频率分布表如下所示.
(1)请先求出频率分布表中x, y相应的数据,再完成下列频率分布直方图;
(2)根据频率分布直方图估计该校学业水平测试数学成绩的平均分;
(3)为选拔优秀学生参加湖南某大学的自主招生,学校决定在第4,5,6组中用分层抽样的方法抽取6名学生参加校内初选,求第4,5,6组各抽取了多少名学生?
组号 分组 频数 频率
第1组 [70,75) 5 0.050
第2组 [75,80) x 0.150
第3组 [80,85) 20 0.200
第4组 [85,90) 30 y
第5组 [90,95) 20 0.200
第6组 [95,100] 10 0.100
合计 100 1.000
18.(本小题满分8分)
如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,,E为PC的中点.
(1)求证:PA∥平面BDE;
(2)求直线PB与平面ABCD所成的角正切值.
19.(本小题满分8分)
某产品的成本由生产成本和营销成本两部分组成. 经调查测算,当全年营销费用(即营销成本)为x(x>0)万元时,该产品的年销售量(即该厂的年产量)为万件,已知2010年全年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均生产成本的1.5倍(年生产成本包括固定投入和再投入两部分资金).
(1)要使2010年该产品的年销售量不低于2万件,厂家的年营销费用至少为多少万元?
(2)将2010年该产品的利润y万元表示为年营销费用x的函数;并求厂家的营销费用x为多少万元时,厂家的年利润y最大?
20.(本小题满分10分)
已知等差数列和正项等比数列,
(1)求数列的通项公式;
(2)若是的等比中项,求数列的通项公式;
(3)在(2)的条件下,设的前n项和为,若对任意的正整数n都成立,求实数λ的最小值.
2010年怀化市高中学业水平模拟测试
数学试题参考答案
一.选择题: BABCD, ACACD
二、填空题:
11.; 12.8; 13.;14. ,; 15.10.
三、解答题:
16.解:(1)由已知 ,又 ,∴ ………………2分
∴ …………………………3分
(2)
∴ …………………………4分
由 得
∴求的周期为,单调递增区间为
…………………………6分
17.解:(1)x=15,y=0.300,频率分布表直方图略. …………………………4分
(2)
故 该校学业水平测试数学成绩的平均分约是86.25分. ……………………6分
(3)第4,5,6组共有60位同学,从中抽取6名学生,抽取比例为,
∴ 第4,5,6组应各抽取3名,2名,1名学生. …………………… 8分
18.(1)证明 连接AC交BD于O,连EO,
由底面ABCD是正方形知 O是AC的中点,
又 E为PC的中点, ∴ PA∥EO,
又
∴ PA∥平面BDE ………………………4分
(2)解:∵ 侧棱PD⊥底面ABCD,
∴ DB是PB在平面ABCD内的射影;
∴ ∠PBD就是直线PB与平面ABCD所成的角,
∴ ,
∴ 直线PB与平面ABCD所成的角正切值为………………………8分
19.解:(1)由已知,,即 ,∴ .
故 厂家2010年的年营销费用至少为2万元. ………………………3分
(2)由题意,每件产品年平均生产成本为 元,
∴
即 ………………………5分
∵ ,
当且仅当 ,即时取等号.
故 年营销费用为4万元时,厂家的利润最大. …………………………8分
20.解:(1)∵ ∴
又 ∴
∴ .…………………………3分
(2)由(1)知 ∴ ,
又是正项数列, ∴ , .…………………………6分
(3)
由题意 即 对任意的正整数n都成立,
令 , 则
∴ , 即 数列递减,.
∴ 实数λ的最小值为3. …………………………10分
70
80
90
100
0.01
0.02
0.04
0.06
0.03
0.05
成绩(分)
频率
组距
O
P
A
B
D
C
E
P
A
B
D
C
E
O
7-5
数 学
命题:怀化市铁路第一中学 向重新 审题 怀化市教科院 唐振球 张理科
时量120分钟,满分100分.
一、选择题:本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则
A. B. C. D.
2.直线l经过点且与直线垂直,则l的方程是
A. B.
C. D.
3.将如图所示的转盘分成五个面积相等的区域,规定:某人随
机转动转盘,当静止时,若指针指向N区域则中奖. 按此规
则,此人中奖的概率是
A. B. C. D.
4.下列函数在定义域中是减函数的是
A. B. C. D.
5.已知平面向量 ,且,则
A.3 B.9 C. D.
6.下面三视图表示的几何体是
A.六棱柱 B.六棱锥 C.六棱台 D.平行六面体
7.将的图象向左平移个单位,所得图象的函数解析式为
A. B.
C. D.
8.函数的零点所在的区间大致是
A.(1.2) B.(2.3) C.(3.4) D.(4.5)
9.圆心坐标是,半径等于的圆的方程是
A. B.
C. D.
10.已知,,,则,,的大小顺序为
A. B. C. D.
二、填空题:本大题共5小题,每小题4分,满分20分.
11.已知函数, 若, 则____________.
12.在平面直角坐标系中,不等式组所围成的平面区域的面积
为_________________.
13.把89化成五进制数结果为_________________.
14.在中,A, B, C所对的边分别为a, b, c, 若
,则________, = .
15.按如右程序框图运行程序,则输出的S= .
三、解答题:本大题共5小题,满分40分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)
已知,.
(1)求的值;
(2)求的周期和单调递增区间.
17.(本小题满分8分)
某校从参加高二学业水平测试的学生中随机抽出100名学生的数学成绩, 按成绩分组,得到频率分布表如下所示.
(1)请先求出频率分布表中x, y相应的数据,再完成下列频率分布直方图;
(2)根据频率分布直方图估计该校学业水平测试数学成绩的平均分;
(3)为选拔优秀学生参加湖南某大学的自主招生,学校决定在第4,5,6组中用分层抽样的方法抽取6名学生参加校内初选,求第4,5,6组各抽取了多少名学生?
组号 分组 频数 频率
第1组 [70,75) 5 0.050
第2组 [75,80) x 0.150
第3组 [80,85) 20 0.200
第4组 [85,90) 30 y
第5组 [90,95) 20 0.200
第6组 [95,100] 10 0.100
合计 100 1.000
18.(本小题满分8分)
如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,,E为PC的中点.
(1)求证:PA∥平面BDE;
(2)求直线PB与平面ABCD所成的角正切值.
19.(本小题满分8分)
某产品的成本由生产成本和营销成本两部分组成. 经调查测算,当全年营销费用(即营销成本)为x(x>0)万元时,该产品的年销售量(即该厂的年产量)为万件,已知2010年全年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均生产成本的1.5倍(年生产成本包括固定投入和再投入两部分资金).
(1)要使2010年该产品的年销售量不低于2万件,厂家的年营销费用至少为多少万元?
(2)将2010年该产品的利润y万元表示为年营销费用x的函数;并求厂家的营销费用x为多少万元时,厂家的年利润y最大?
20.(本小题满分10分)
已知等差数列和正项等比数列,
(1)求数列的通项公式;
(2)若是的等比中项,求数列的通项公式;
(3)在(2)的条件下,设的前n项和为,若对任意的正整数n都成立,求实数λ的最小值.
2010年怀化市高中学业水平模拟测试
数学试题参考答案
一.选择题: BABCD, ACACD
二、填空题:
11.; 12.8; 13.;14. ,; 15.10.
三、解答题:
16.解:(1)由已知 ,又 ,∴ ………………2分
∴ …………………………3分
(2)
∴ …………………………4分
由 得
∴求的周期为,单调递增区间为
…………………………6分
17.解:(1)x=15,y=0.300,频率分布表直方图略. …………………………4分
(2)
故 该校学业水平测试数学成绩的平均分约是86.25分. ……………………6分
(3)第4,5,6组共有60位同学,从中抽取6名学生,抽取比例为,
∴ 第4,5,6组应各抽取3名,2名,1名学生. …………………… 8分
18.(1)证明 连接AC交BD于O,连EO,
由底面ABCD是正方形知 O是AC的中点,
又 E为PC的中点, ∴ PA∥EO,
又
∴ PA∥平面BDE ………………………4分
(2)解:∵ 侧棱PD⊥底面ABCD,
∴ DB是PB在平面ABCD内的射影;
∴ ∠PBD就是直线PB与平面ABCD所成的角,
∴ ,
∴ 直线PB与平面ABCD所成的角正切值为………………………8分
19.解:(1)由已知,,即 ,∴ .
故 厂家2010年的年营销费用至少为2万元. ………………………3分
(2)由题意,每件产品年平均生产成本为 元,
∴
即 ………………………5分
∵ ,
当且仅当 ,即时取等号.
故 年营销费用为4万元时,厂家的利润最大. …………………………8分
20.解:(1)∵ ∴
又 ∴
∴ .…………………………3分
(2)由(1)知 ∴ ,
又是正项数列, ∴ , .…………………………6分
(3)
由题意 即 对任意的正整数n都成立,
令 , 则
∴ , 即 数列递减,.
∴ 实数λ的最小值为3. …………………………10分
70
80
90
100
0.01
0.02
0.04
0.06
0.03
0.05
成绩(分)
频率
组距
O
P
A
B
D
C
E
P
A
B
D
C
E
O
7-5
同课章节目录
