沪科版数学九年级上第22章相似形综合测试题及答案
文档属性
| 名称 | 沪科版数学九年级上第22章相似形综合测试题及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 20:04:35 | ||
图片预览


文档简介
沪九(上)第23章相似形综合测试题及答案
一、选择题
小敏的圆规摆放如图所示,则几个和小明的圆规形状一样的圆规中,与小明摆放的位似的是( )
A.
B.
C.
D.
2.已知如图:(1)、(2)中各有两个三
( http: / / www.21cnjy.com )角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于0点,对于各图中的两个三角形而言,下列说法正确的是( )
A.都相似
B.都不相似
C.只有(1)相似
D.只有(2)相似
3.已知△MNP如图所示,则下列四个三角形中与△MNP相似的是( )
A.
B.
C.
D.
4.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A.
B.
C.
D.
5.具备下列各组条件的两个三角形中,不一定相似的是(
)
A.有一个角是36°的两个等腰三角形
B.有一个角为108°的两个等腰三角形
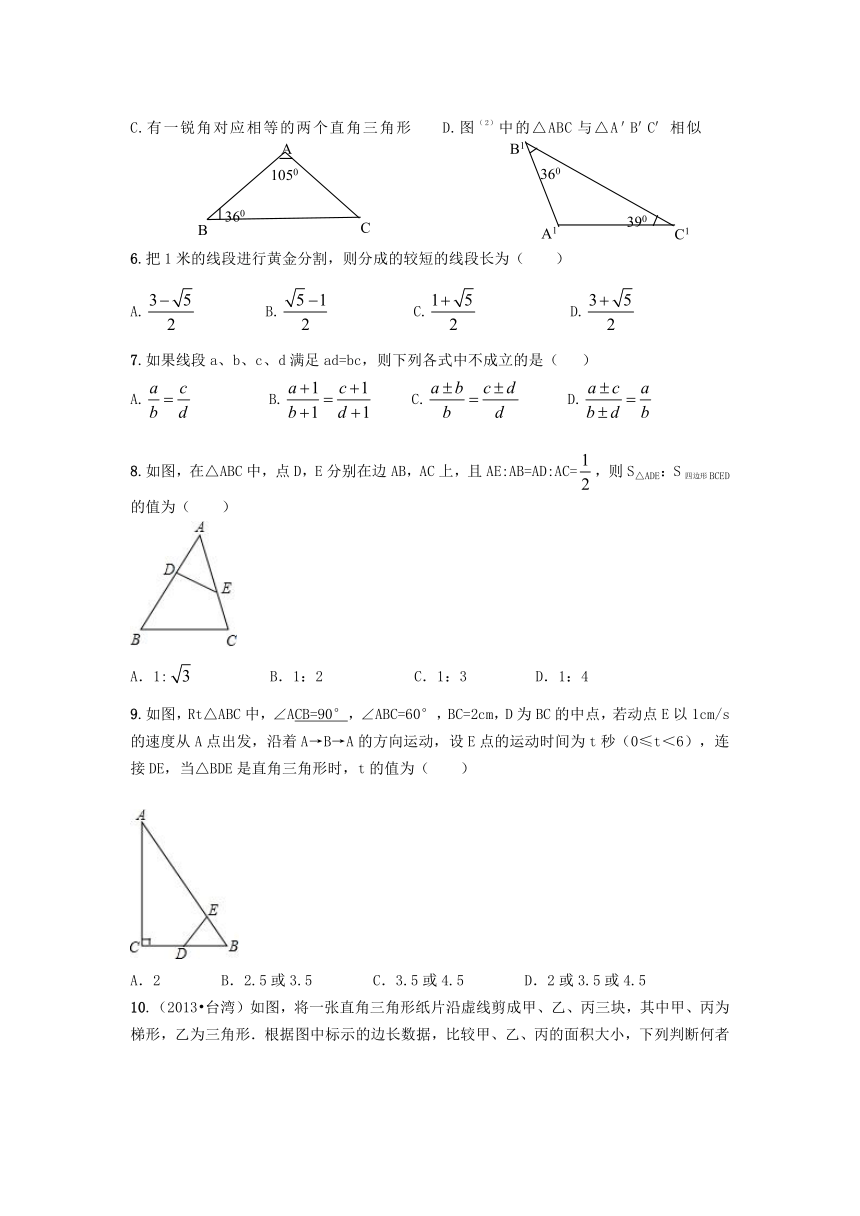
C.有一锐角对应相等的两个直角三角形
D.图(2)中的△ABC与△A'B'C'相似
6.把1米的线段进行黄金分割,则分成的较短的线段长为(
)
A.
B.
C.
D.
7.如果线段a、b、c、d满足ad=bc,则下列各式中不成立的是(
)
A.
B.
C.
D.
8.如图,在△ABC中,点D,E分别在边AB,AC上,且AE:AB=AD:AC=,则S△ADE:S四边形BCED的值为( )
A.1:
B.1:2
C.1:3
D.1:4
9.如图,Rt△ABC中,∠ACB=90°
( http: / / www.21cnjy.com ),∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
10.(2013 台湾)如图,将一张直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断何者正确?( )
A.甲>乙,乙>丙
B.甲>乙,乙<丙
C.甲<乙,乙>丙
D.甲<乙,乙<丙
二、填空题
11.已知a:b:c=2:3:4,且a-2b+3c=20,则a+2b-3c=
.
12.由三角形三边中位线所围成的三角形的面积是原三角形面积的
.
13.如右图,在平行四边形ABCD中,AB
( http: / / www.21cnjy.com )=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=_________cm.
14.小明在测量楼高时,先
( http: / / www.21cnjy.com )测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为_________m.
15.在△ABC中,AB>BC>AC,D是AC的中点,过D作直线l,使截得的三角形与原三角形相似,这样的直线有
条.
16.如图,点A1,A2,A3,A4在
( http: / / www.21cnjy.com )射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为_________.
10.5
三、解答题
17.如图,小明同学用自制的直角三
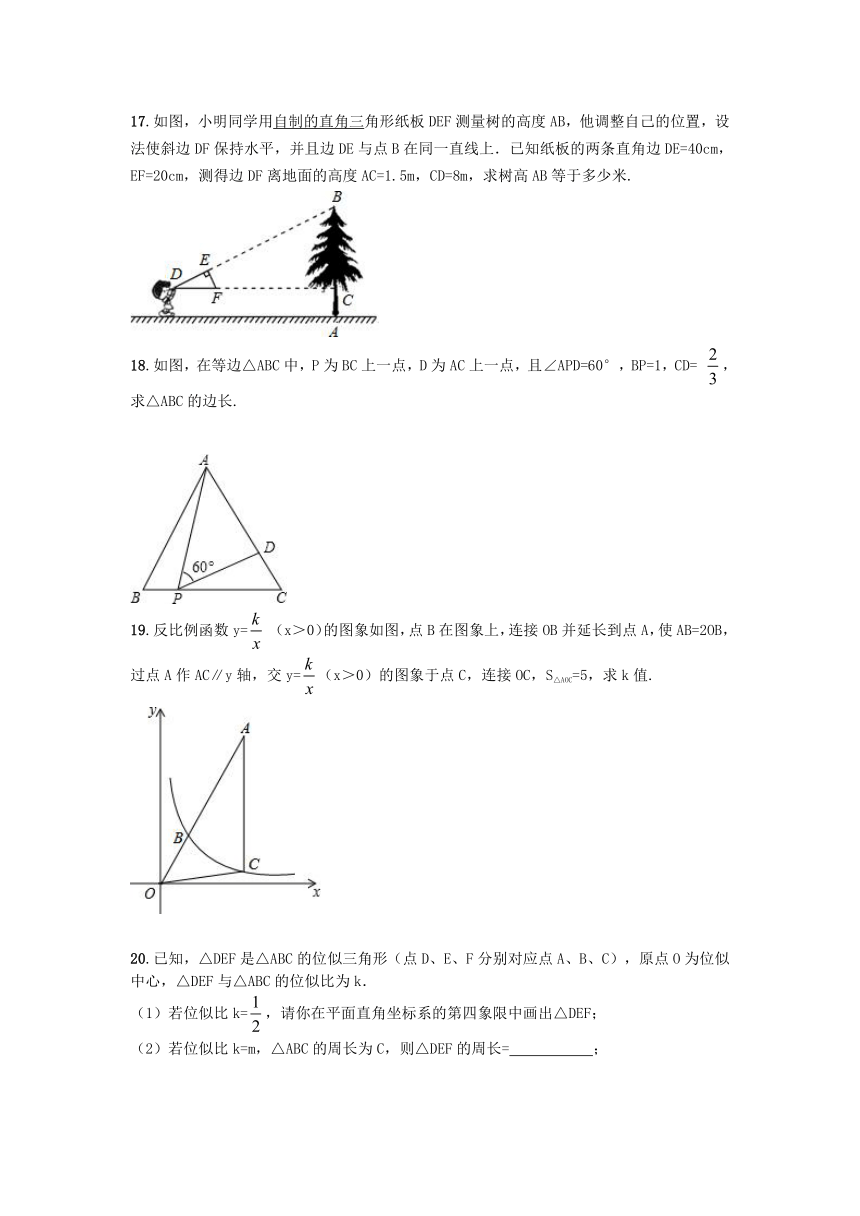
( http: / / www.21cnjy.com )角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB等于多少米.
18.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=
,求△ABC的边长.
19.反比例函数y=
(x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=(x>0)的图象于点C,连接OC,S△AOC=5,求k值.
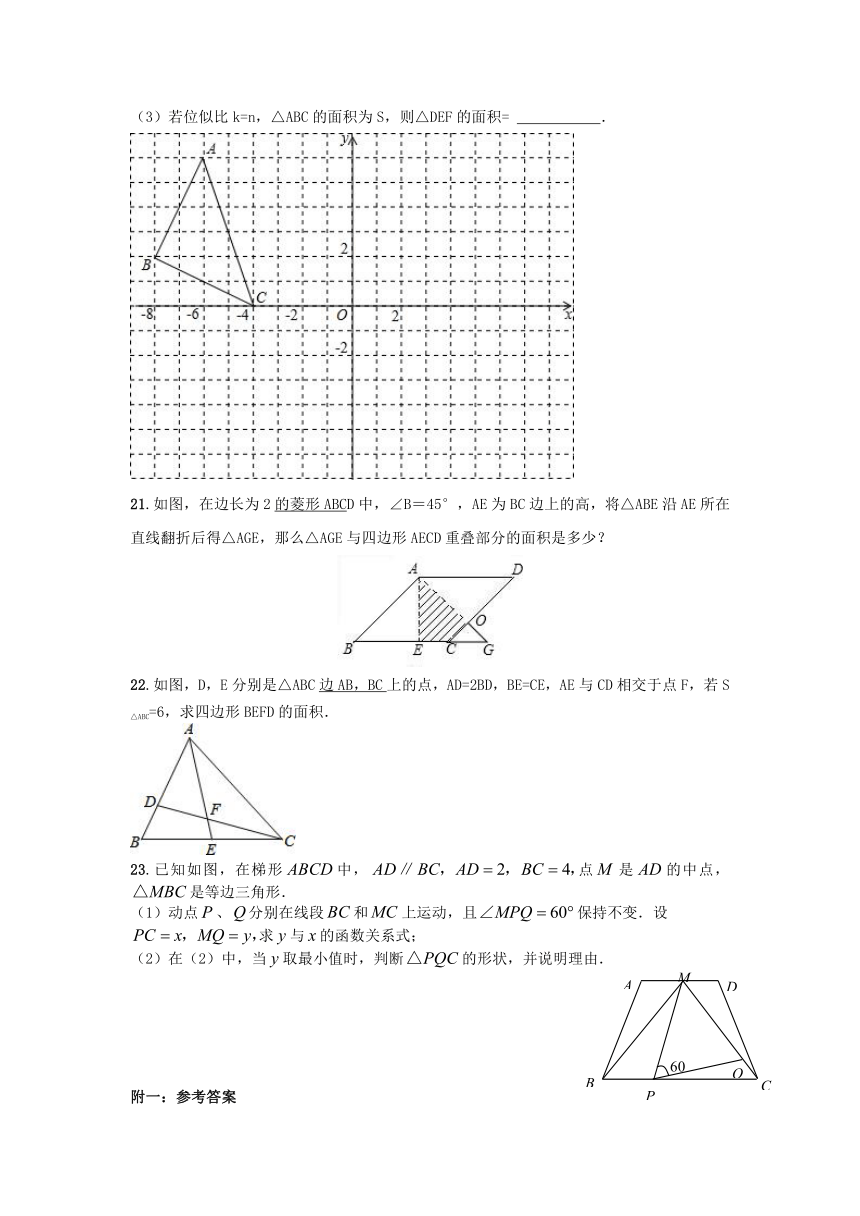
20.已知,△DEF是△ABC的位似三角形(点D、E、F分别对应点A、B、C),原点O为位似中心,△DEF与△ABC的位似比为k.
(1)若位似比k=,请你在平面直角坐标系的第四象限中画出△DEF;
(2)若位似比k=m,△ABC的周长为C,则△DEF的周长=
mC;
(3)若位似比k=n,△ABC的面积为S,则△DEF的面积=
n2S.
21.如图,在边长为2的菱形ABC
( http: / / www.21cnjy.com )D中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
22.如图,D,E分别是△ABC边AB,BC
( http: / / www.21cnjy.com )上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
23.已知如图,在梯形中,点是的中点,是等边三角形.
(1)动点、分别在线段和上运动,且保持不变.设
求与的函数关系式;
(2)在(2)中,当取最小值时,判断的形状,并说明理由.
附一:参考答案
一、1、D
2、A
3、C
4、B
5、A
6、A
7、B
8、C
9.D提示:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,∴AB=2BC=4(cm),
∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发,
∴BD=BC=1(cm),BE=AB-AE=4-t(cm),若∠BED=90°,
当A→B时,∵∠ABC=60°,
∴∠BDE=30°,
∴BE=BD=(cm),∴t=3.5,
当B→A时,t=4+0.5=4.5.
若∠BDE=90°时,
当A→B时,∵∠ABC=60°,
∴∠BED=30°,
∴BE=2BD=2(cm),
∴t=4-2=2,
当B→A时,t=4+2=6(舍去).
综上可得:t的值为2或3.5或4.5.
10.D提示:首先过点B作BH⊥GF于点H,则S乙=AB AC,易证得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的长,继而求得答案.∴甲<乙,乙<丙.故选D.
二、11.-10;
12.
;
13.;
14.10m提示:在同一时
( http: / / www.21cnjy.com )刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.
15.4;
16.10.5提示:已知
( http: / / www.21cnjy.com )△A2B1B2,△A3B2B3的面积分别为1,4,且两三角形相似,因此可得出A2B2:A3B3=1:2,由于△A2B2A3与△B2A3B3是等高不等底的三角形,所以面积之比即为底边之比,因此这两个三角形的面积比为1:2,根据△A3B2B3的面积为4,可求出△A2B2A3的面积,同理可求出△A3B3A4和△A1B1A2的面积.即可求出阴影部分的面积.
三、17.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,∴BC:EF=DC:DE.
∵DE=40cm=0.4m,EF=20
( http: / / www.21cnjy.com )cm=0.2m,AC=1.5m,CD=8m,
∴BC:0.2=8:0.4,∴BC=4米,∴AB=AC+BC=1.5+4=5.5米,
故树高5.5米.
18.解:设△ABC的边长为x,
∵△ABC是等边三角形,
∴∠DCP=∠PBA=60°.
∵∠APC=∠APD+∠DPC=∠BAP+∠ABP,∠APD=60°,
∴∠BAP=∠CPD.
∴△ABP∽△CPD.
∴BP:DC=AB:PC,
∴,∴x=3.即△ABC的边长为3.
19.解:作BD⊥x轴于D,延长AC交x轴于E,如图,
∵AC∥y轴,
∴BD∥AE,
∴△OBD∽△OAE,
∴BD:AE=OD:OE=OB:OA,
而AB=2OB,
∴BD:AE=OD:OE=1:3,
设OD=t,则OE=3t,
∵B点和C点在反比例函数y=
,(x>0)的图象上,
∴B点坐标为(t,),
∴BD=,
∴AE=,
∵S△AOC=S△AOE-S△COE,
∴ 3t k=5,
∴k=.
20.解:(1)如图所示,
则△DEF为所求的三角形;
(2)∵位似比k=m,△ABC的周长为C,
∴△DEF的周长=mC;
(3)∵位似比k=n,△ABC的面积为S,
∴△DEF的面积=n2S.
21.解:∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,∴AE=.
由折叠易得△AEG和△OCG为等腰直角三角形,∴.
设OC=OG=
x,则AO=2-x,CG=x.
由△ODA∽△OCG得,即,解得.
∴.
∴重叠部分的面积为
22.解:∵AD=2BD,S△ABC=6,∴S△ADC=S△ABC=4,S△BDC=S△ABC=2.
过E作EG∥AB交CD于G,
∵BE=CE,∴CG=DG,∴BD=2EG,
∵AD=2BD,∴AD=4EG.设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴S△CEG:
S△CBD=()2=,
∴S△CEG=S△CBD=×2=,S梯形EGDB=2-=,
设S△FEG=x,则S四边形BEFD=-x,
∵S△ABE=S△ABC=3,
∴S△ADF=S△ABE-S四边形BEFD=3-(-x)=+x.
∵EG∥AD,∴△FEG∽△FAD,
∴S△FEG:
S△FAD=()2=
,
∴S△FAD=16S△FEG=16x,
∴16x=
+x,解得x=
,
∴S四边形BEFD=
-x=-=
.
23.(1)解:在等边中,
∴
∴
∴
∴
∵
∴
∴
∴
(2)解:
为直角三角形
∵
∴当取最小值时,
∴是的中点,而
∴
∴
B1
A1
C1
360
390
A
B
C
1050
360
D
C
A
B
E
F
A
D
C
B
P
M
Q
60°
一、选择题
小敏的圆规摆放如图所示,则几个和小明的圆规形状一样的圆规中,与小明摆放的位似的是( )
A.
B.
C.
D.
2.已知如图:(1)、(2)中各有两个三
( http: / / www.21cnjy.com )角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于0点,对于各图中的两个三角形而言,下列说法正确的是( )
A.都相似
B.都不相似
C.只有(1)相似
D.只有(2)相似
3.已知△MNP如图所示,则下列四个三角形中与△MNP相似的是( )
A.
B.
C.
D.
4.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A.
B.
C.
D.
5.具备下列各组条件的两个三角形中,不一定相似的是(
)
A.有一个角是36°的两个等腰三角形
B.有一个角为108°的两个等腰三角形
C.有一锐角对应相等的两个直角三角形
D.图(2)中的△ABC与△A'B'C'相似
6.把1米的线段进行黄金分割,则分成的较短的线段长为(
)
A.
B.
C.
D.
7.如果线段a、b、c、d满足ad=bc,则下列各式中不成立的是(
)
A.
B.
C.
D.
8.如图,在△ABC中,点D,E分别在边AB,AC上,且AE:AB=AD:AC=,则S△ADE:S四边形BCED的值为( )
A.1:
B.1:2
C.1:3
D.1:4
9.如图,Rt△ABC中,∠ACB=90°
( http: / / www.21cnjy.com ),∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
10.(2013 台湾)如图,将一张直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断何者正确?( )
A.甲>乙,乙>丙
B.甲>乙,乙<丙
C.甲<乙,乙>丙
D.甲<乙,乙<丙
二、填空题
11.已知a:b:c=2:3:4,且a-2b+3c=20,则a+2b-3c=
.
12.由三角形三边中位线所围成的三角形的面积是原三角形面积的
.
13.如右图,在平行四边形ABCD中,AB
( http: / / www.21cnjy.com )=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=_________cm.
14.小明在测量楼高时,先
( http: / / www.21cnjy.com )测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为_________m.
15.在△ABC中,AB>BC>AC,D是AC的中点,过D作直线l,使截得的三角形与原三角形相似,这样的直线有
条.
16.如图,点A1,A2,A3,A4在
( http: / / www.21cnjy.com )射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为_________.
10.5
三、解答题
17.如图,小明同学用自制的直角三
( http: / / www.21cnjy.com )角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB等于多少米.
18.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=
,求△ABC的边长.
19.反比例函数y=
(x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=(x>0)的图象于点C,连接OC,S△AOC=5,求k值.
20.已知,△DEF是△ABC的位似三角形(点D、E、F分别对应点A、B、C),原点O为位似中心,△DEF与△ABC的位似比为k.
(1)若位似比k=,请你在平面直角坐标系的第四象限中画出△DEF;
(2)若位似比k=m,△ABC的周长为C,则△DEF的周长=
mC;
(3)若位似比k=n,△ABC的面积为S,则△DEF的面积=
n2S.
21.如图,在边长为2的菱形ABC
( http: / / www.21cnjy.com )D中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
22.如图,D,E分别是△ABC边AB,BC
( http: / / www.21cnjy.com )上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
23.已知如图,在梯形中,点是的中点,是等边三角形.
(1)动点、分别在线段和上运动,且保持不变.设
求与的函数关系式;
(2)在(2)中,当取最小值时,判断的形状,并说明理由.
附一:参考答案
一、1、D
2、A
3、C
4、B
5、A
6、A
7、B
8、C
9.D提示:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,∴AB=2BC=4(cm),
∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发,
∴BD=BC=1(cm),BE=AB-AE=4-t(cm),若∠BED=90°,
当A→B时,∵∠ABC=60°,
∴∠BDE=30°,
∴BE=BD=(cm),∴t=3.5,
当B→A时,t=4+0.5=4.5.
若∠BDE=90°时,
当A→B时,∵∠ABC=60°,
∴∠BED=30°,
∴BE=2BD=2(cm),
∴t=4-2=2,
当B→A时,t=4+2=6(舍去).
综上可得:t的值为2或3.5或4.5.
10.D提示:首先过点B作BH⊥GF于点H,则S乙=AB AC,易证得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的长,继而求得答案.∴甲<乙,乙<丙.故选D.
二、11.-10;
12.
;
13.;
14.10m提示:在同一时
( http: / / www.21cnjy.com )刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.
15.4;
16.10.5提示:已知
( http: / / www.21cnjy.com )△A2B1B2,△A3B2B3的面积分别为1,4,且两三角形相似,因此可得出A2B2:A3B3=1:2,由于△A2B2A3与△B2A3B3是等高不等底的三角形,所以面积之比即为底边之比,因此这两个三角形的面积比为1:2,根据△A3B2B3的面积为4,可求出△A2B2A3的面积,同理可求出△A3B3A4和△A1B1A2的面积.即可求出阴影部分的面积.
三、17.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,∴BC:EF=DC:DE.
∵DE=40cm=0.4m,EF=20
( http: / / www.21cnjy.com )cm=0.2m,AC=1.5m,CD=8m,
∴BC:0.2=8:0.4,∴BC=4米,∴AB=AC+BC=1.5+4=5.5米,
故树高5.5米.
18.解:设△ABC的边长为x,
∵△ABC是等边三角形,
∴∠DCP=∠PBA=60°.
∵∠APC=∠APD+∠DPC=∠BAP+∠ABP,∠APD=60°,
∴∠BAP=∠CPD.
∴△ABP∽△CPD.
∴BP:DC=AB:PC,
∴,∴x=3.即△ABC的边长为3.
19.解:作BD⊥x轴于D,延长AC交x轴于E,如图,
∵AC∥y轴,
∴BD∥AE,
∴△OBD∽△OAE,
∴BD:AE=OD:OE=OB:OA,
而AB=2OB,
∴BD:AE=OD:OE=1:3,
设OD=t,则OE=3t,
∵B点和C点在反比例函数y=
,(x>0)的图象上,
∴B点坐标为(t,),
∴BD=,
∴AE=,
∵S△AOC=S△AOE-S△COE,
∴ 3t k=5,
∴k=.
20.解:(1)如图所示,
则△DEF为所求的三角形;
(2)∵位似比k=m,△ABC的周长为C,
∴△DEF的周长=mC;
(3)∵位似比k=n,△ABC的面积为S,
∴△DEF的面积=n2S.
21.解:∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,∴AE=.
由折叠易得△AEG和△OCG为等腰直角三角形,∴.
设OC=OG=
x,则AO=2-x,CG=x.
由△ODA∽△OCG得,即,解得.
∴.
∴重叠部分的面积为
22.解:∵AD=2BD,S△ABC=6,∴S△ADC=S△ABC=4,S△BDC=S△ABC=2.
过E作EG∥AB交CD于G,
∵BE=CE,∴CG=DG,∴BD=2EG,
∵AD=2BD,∴AD=4EG.设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴S△CEG:
S△CBD=()2=,
∴S△CEG=S△CBD=×2=,S梯形EGDB=2-=,
设S△FEG=x,则S四边形BEFD=-x,
∵S△ABE=S△ABC=3,
∴S△ADF=S△ABE-S四边形BEFD=3-(-x)=+x.
∵EG∥AD,∴△FEG∽△FAD,
∴S△FEG:
S△FAD=()2=
,
∴S△FAD=16S△FEG=16x,
∴16x=
+x,解得x=
,
∴S四边形BEFD=
-x=-=
.
23.(1)解:在等边中,
∴
∴
∴
∴
∵
∴
∴
∴
(2)解:
为直角三角形
∵
∴当取最小值时,
∴是的中点,而
∴
∴
B1
A1
C1
360
390
A
B
C
1050
360
D
C
A
B
E
F
A
D
C
B
P
M
Q
60°
