2016-2017学年九年级数学(湘教版)上册课件:3.6位似
文档属性
| 名称 | 2016-2017学年九年级数学(湘教版)上册课件:3.6位似 |  | |
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 15:24:29 | ||
图片预览



文档简介
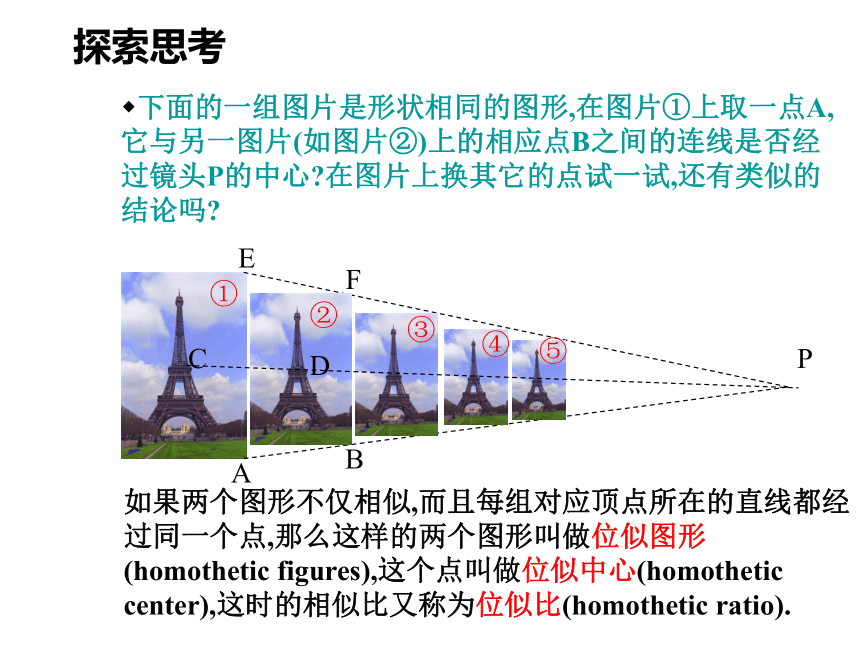
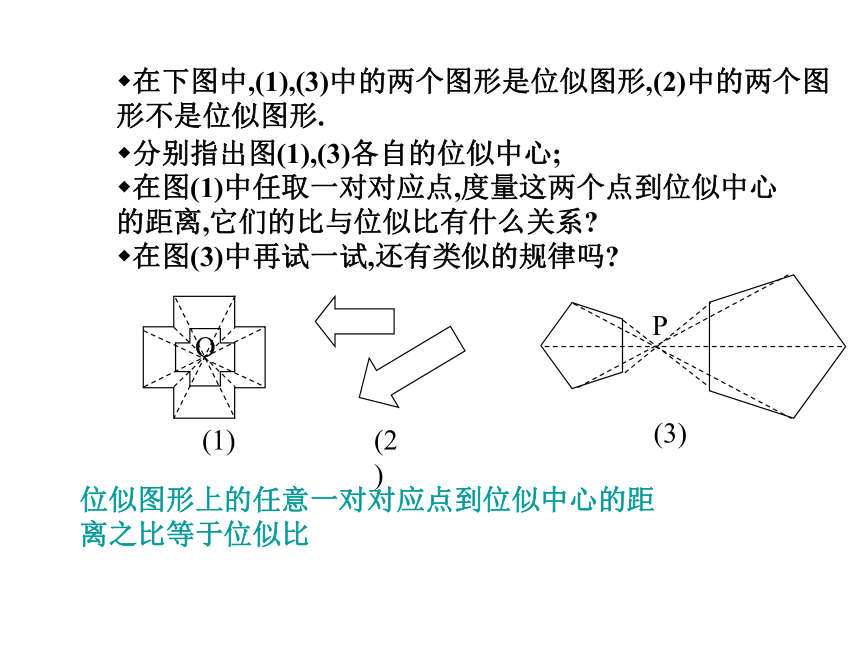
课件15张PPT。3.6 位似下面的一组图片是形状相同的图形,在图片①上取一点A,它与另一图片(如图片②)上的相应点B之间的连线是否经过镜头P的中心?在图片上换其它的点试一试,还有类似的结论吗?如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形(homothetic figures),这个点叫做位似中心(homothetic center),这时的相似比又称为位似比(homothetic ratio).①PA②③④⑤BCDEF探索思考在下图中,(1),(3)中的两个图形是位似图形,(2)中的两个图形不是位似图形.分别指出图(1),(3)各自的位似中心;
在图(1)中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系?
在图(3)中再试一试,还有类似的规律吗?位似图形上的任意一对对应点到位似中心的距离之比等于位似比你还记得本章第三节<做一做>用橡皮筋放大图形的方法吗?
实际上,使用这种方法,放大前后的两个图形是位似图形.
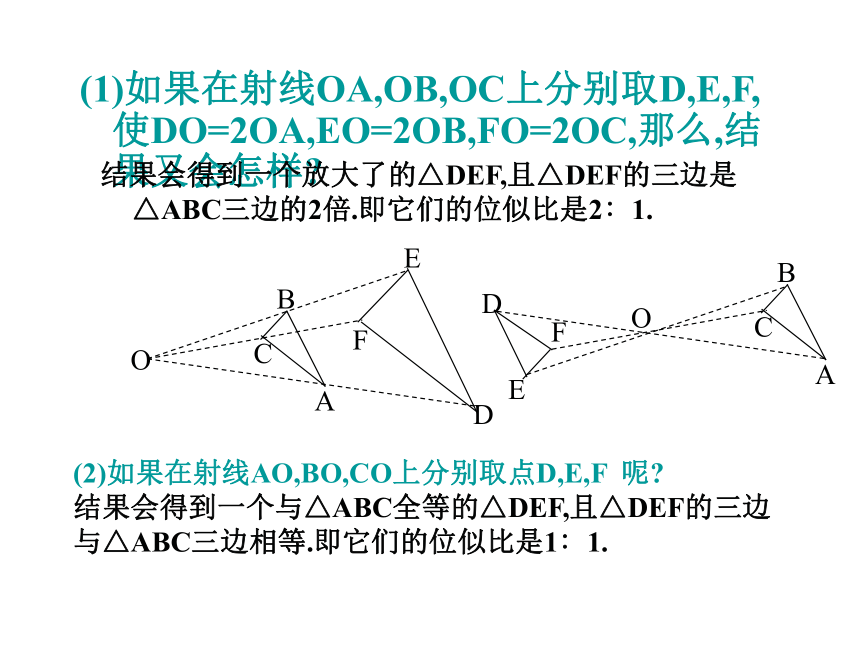
你能用这种方法将一个已知的多边形放大,使放大后的图形与原来图形的位似比分别是3和4吗?按如下方法可以将△ABC的三边缩小为原来的1/2:O如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;△DEF的三边就是△ABC相应三边的1/2. 实际上△ABC与△DEF是位似图形.实践出真知,一起来动手: 任意画一个三角形,用上面的方法 亲自试一试.探索实践(1)如果在射线OA,OB,OC上分别取D,E,F,使DO=2OA,EO=2OB,FO=2OC,那么,结果又会怎样?(2)如果在射线AO,BO,CO上分别取点D,E,F 呢?
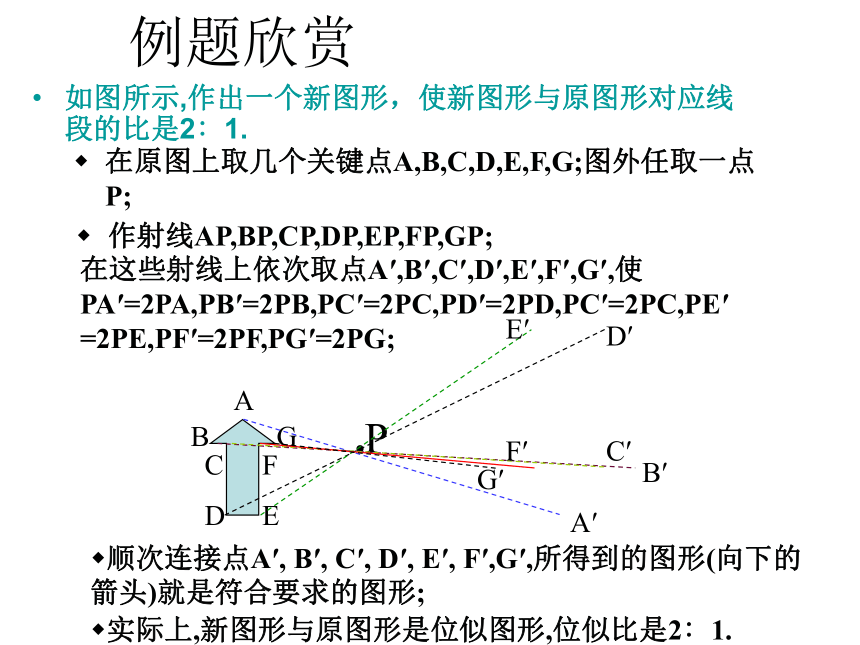
结果会得到一个与△ABC全等的△DEF,且△DEF的三边与△ABC三边相等.即它们的位似比是1∶1.结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1.例题欣赏如图所示,作出一个新图形,使新图形与原图形对应线段的比是2∶1.在原图上取几个关键点A,B,C,D,E,F,G;图外任取一点P;作射线AP,BP,CP,DP,EP,FP,GP;在这些射线上依次取点A′,B′,C′,D′,E′,F′,G′,使PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PC′=2PC,PE′ =2PE,PF′=2PF,PG′=2PG;顺次连接点A′, B′, C′, D′, E′, F′,G′,所得到的图形(向下的箭头)就是符合要求的图形;实际上,新图形与原图形是位似图形,位似比是2∶1.如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).2120- 2- 1- 20探索思考如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?ABC 位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).4642124-4-6-4-2-4-12A'B'C'A"B"C"例 如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为 的位似图形.分析:问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律,点A的对应点A‘的坐标为 ,即(-3,3).类似地,可以确定其他顶点的坐标.解:如图,利用位似变换中对应点的坐标的变化规律.分别取点
A'( , ),B ' ( , ),
C ' ( , ),D'( , ).ABCDA'B'C'D'- 33- 41-20-12依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形.例题分析在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.课堂练习下面的说法对吗?为什么?
分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;
分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形;
分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;(正确)(正确)(错误)
1. 如图表示△AOB和把它缩小后得到的△COD,求它们的相似比.点D的横坐标为2点B的横坐标为5相似比为2. 如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.ABC解:
A'( , ),B ' ( , ),C ' ( , ),4- 4- 108-410A" ( , ),B" ( , ),C" ( , ),4- 4- 810-104A'B 'C 'A"B"C"位似多边形:
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形(homothetic figures),这个点叫做位似中心(homothetic center),这时的相似比又称为位似比(homothetic ratio).
位似图形上的任意一对对应点到位似中心的距离之比等于位似比
如何作位似图形(放大与缩小;正像与倒像).课堂小结
在图(1)中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系?
在图(3)中再试一试,还有类似的规律吗?位似图形上的任意一对对应点到位似中心的距离之比等于位似比你还记得本章第三节<做一做>用橡皮筋放大图形的方法吗?
实际上,使用这种方法,放大前后的两个图形是位似图形.
你能用这种方法将一个已知的多边形放大,使放大后的图形与原来图形的位似比分别是3和4吗?按如下方法可以将△ABC的三边缩小为原来的1/2:O如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F;△DEF的三边就是△ABC相应三边的1/2. 实际上△ABC与△DEF是位似图形.实践出真知,一起来动手: 任意画一个三角形,用上面的方法 亲自试一试.探索实践(1)如果在射线OA,OB,OC上分别取D,E,F,使DO=2OA,EO=2OB,FO=2OC,那么,结果又会怎样?(2)如果在射线AO,BO,CO上分别取点D,E,F 呢?
结果会得到一个与△ABC全等的△DEF,且△DEF的三边与△ABC三边相等.即它们的位似比是1∶1.结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1.例题欣赏如图所示,作出一个新图形,使新图形与原图形对应线段的比是2∶1.在原图上取几个关键点A,B,C,D,E,F,G;图外任取一点P;作射线AP,BP,CP,DP,EP,FP,GP;在这些射线上依次取点A′,B′,C′,D′,E′,F′,G′,使PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PC′=2PC,PE′ =2PE,PF′=2PF,PG′=2PG;顺次连接点A′, B′, C′, D′, E′, F′,G′,所得到的图形(向下的箭头)就是符合要求的图形;实际上,新图形与原图形是位似图形,位似比是2∶1.如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).2120- 2- 1- 20探索思考如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?ABC 位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).4642124-4-6-4-2-4-12A'B'C'A"B"C"例 如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为 的位似图形.分析:问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律,点A的对应点A‘的坐标为 ,即(-3,3).类似地,可以确定其他顶点的坐标.解:如图,利用位似变换中对应点的坐标的变化规律.分别取点
A'( , ),B ' ( , ),
C ' ( , ),D'( , ).ABCDA'B'C'D'- 33- 41-20-12依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形.例题分析在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.课堂练习下面的说法对吗?为什么?
分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;
分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形;
分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形;(正确)(正确)(错误)
1. 如图表示△AOB和把它缩小后得到的△COD,求它们的相似比.点D的横坐标为2点B的横坐标为5相似比为2. 如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.ABC解:
A'( , ),B ' ( , ),C ' ( , ),4- 4- 108-410A" ( , ),B" ( , ),C" ( , ),4- 4- 810-104A'B 'C 'A"B"C"位似多边形:
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形(homothetic figures),这个点叫做位似中心(homothetic center),这时的相似比又称为位似比(homothetic ratio).
位似图形上的任意一对对应点到位似中心的距离之比等于位似比
如何作位似图形(放大与缩小;正像与倒像).课堂小结
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
