2016-2017学年九年级数学(湘教版)上册课件:4.1正弦和余弦 (共17张PPT)
文档属性
| 名称 | 2016-2017学年九年级数学(湘教版)上册课件:4.1正弦和余弦 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 272.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 14:29:01 | ||
图片预览





文档简介
课件17张PPT。第4章 锐角三角函数4.1正弦和余弦 教学过程创设情境,导入新课 1.你知道直角三角形有哪些特殊的性质吗?
2.有一个锐角是30°的直角三角形有哪些性质特点?
3.有一个锐角是45°的直角三角形有那些性质特点?
教师提出问题,学生复习回答,尝试发现直角三角形中的某些规律.教师汇总归纳,引入新课. 每位同学画一个直角三角形,其中一个锐角为65o ,量出65o角的对边长度和斜边长度,计算:的值,结论:在有一个锐角为65o的直角三角形中, 65o角的对边与
斜边的比值是一个常数,它约等于0.91. 1.请同学们测量手中一副三角板中30°、45°角所对的边与斜边的长度,求出它们的比值,结合所学同组内学生交流,能发现什么规律?
规律:不论三角板大小,30°、45°、60°角的对边与斜边的比值是个固定值.
2.若是普通直角三角形,当一个锐角的度数固定时,这个角的对边与斜边的比值是否也是固定值呢? 合作探究,理解新知 学生组内讨论探索
(学生画图并运用三角形相似知识加以证明)
规律:(1)直角三角形中,锐角大小确定后,这个角的对边与斜边的比值随之确定;
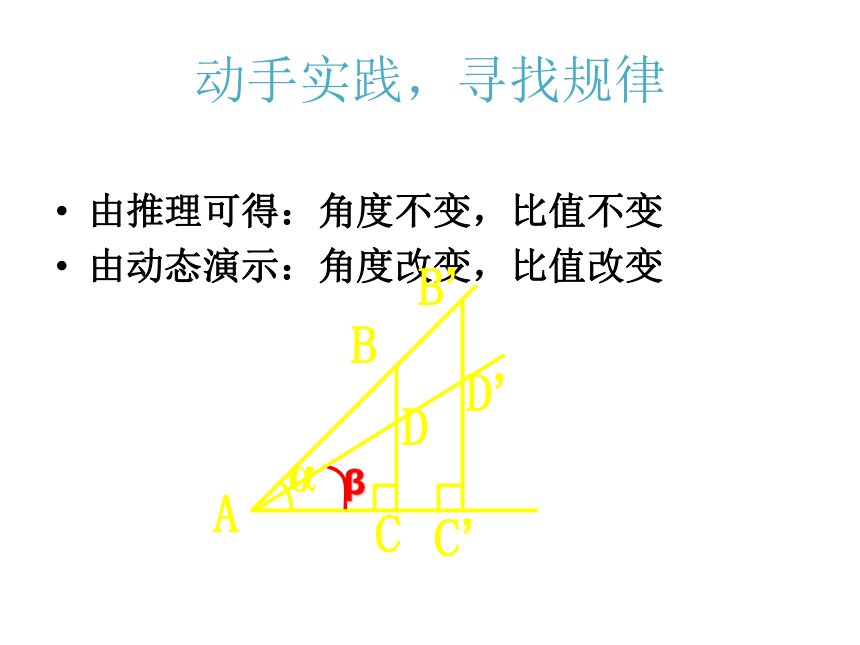
(2)直角三角形中一个锐角的度数越大,它的对边与斜边的比值越大. 动手实践,寻找规律由推理可得:角度不变,比值不变
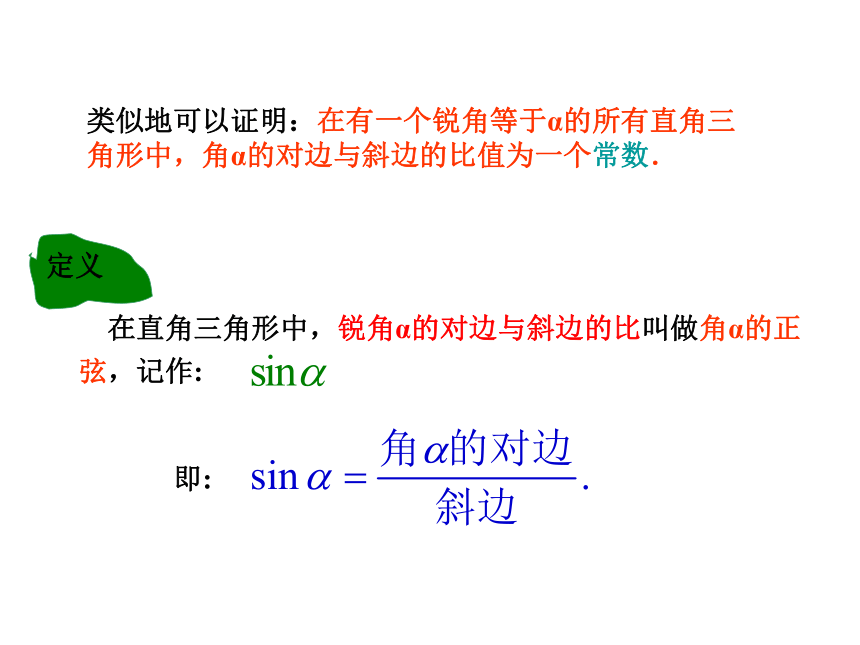
由动态演示:角度改变,比值改变ABCαB’C’β 在直角三角形中,锐角α的对边与斜边的比叫做角α的正弦,记作:类似地可以证明:在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值为一个常数.即: 在直角三角形ABC中, ∠C= 90o, BC=3,AB=5. (1) ∠A的对边BC=3,斜边
AB=5.于是(2) ∠B的对边是AC.根据勾股定理,得于是 AC=4.因此 解 在直角三角形ABC中, ∠C= 90o, ∠A =45°. 于是 ∠B =45°.从而 AC=BC.根据勾股定理,得于是因此画一个直角三角形ABC,使得∠A = 50°,量出∠A的对边BC的长度为3cm,斜边AB的长度为3.9cm.则不足:角的大小、线段的长度都有测量误差,因此精确度不太高,且费时间,效率低.用计算器求.用计算器求锐角的正弦值,要用到 键: 例如:求sin16° ,sin42°的值.sinsin160.275 637 355420.669 130 606==由于计算器的型号与功能的不同,按相应的说明书使用.sin 如图,△ABC 和 △DEF都是直角三角形,它们都有一个锐角等于α,即∠D =∠A = α.在
Rt △ABC 中, ∠A的相邻的直角边(简称邻边)为AC,斜边为AB;在Rt △DEF中,∠D的邻边为DF,斜边为DE.问成立吗?∠B =90°-α=∠E ,AC 是∠B的对边,DF是∠E的对边,
依据正弦定理结论成立在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,记作 这证明了:在有一个锐角等于α的所有直角三角形中,角α的邻边与斜边的比值等于角90°-α的对边与斜边的比值.根据上述证明过程看出:对于任意锐角α,有答案:答案:3 .对于任意锐角α,都有你能说出道理吗?∵AC<AB答案:答案:答案:4.用计算器求下列锐角的正弦值和余弦值(精确到0.0001):35°68°88°9°30°18′76°18′9°38′81°53′
2.有一个锐角是30°的直角三角形有哪些性质特点?
3.有一个锐角是45°的直角三角形有那些性质特点?
教师提出问题,学生复习回答,尝试发现直角三角形中的某些规律.教师汇总归纳,引入新课. 每位同学画一个直角三角形,其中一个锐角为65o ,量出65o角的对边长度和斜边长度,计算:的值,结论:在有一个锐角为65o的直角三角形中, 65o角的对边与
斜边的比值是一个常数,它约等于0.91. 1.请同学们测量手中一副三角板中30°、45°角所对的边与斜边的长度,求出它们的比值,结合所学同组内学生交流,能发现什么规律?
规律:不论三角板大小,30°、45°、60°角的对边与斜边的比值是个固定值.
2.若是普通直角三角形,当一个锐角的度数固定时,这个角的对边与斜边的比值是否也是固定值呢? 合作探究,理解新知 学生组内讨论探索
(学生画图并运用三角形相似知识加以证明)
规律:(1)直角三角形中,锐角大小确定后,这个角的对边与斜边的比值随之确定;
(2)直角三角形中一个锐角的度数越大,它的对边与斜边的比值越大. 动手实践,寻找规律由推理可得:角度不变,比值不变
由动态演示:角度改变,比值改变ABCαB’C’β 在直角三角形中,锐角α的对边与斜边的比叫做角α的正弦,记作:类似地可以证明:在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值为一个常数.即: 在直角三角形ABC中, ∠C= 90o, BC=3,AB=5. (1) ∠A的对边BC=3,斜边
AB=5.于是(2) ∠B的对边是AC.根据勾股定理,得于是 AC=4.因此 解 在直角三角形ABC中, ∠C= 90o, ∠A =45°. 于是 ∠B =45°.从而 AC=BC.根据勾股定理,得于是因此画一个直角三角形ABC,使得∠A = 50°,量出∠A的对边BC的长度为3cm,斜边AB的长度为3.9cm.则不足:角的大小、线段的长度都有测量误差,因此精确度不太高,且费时间,效率低.用计算器求.用计算器求锐角的正弦值,要用到 键: 例如:求sin16° ,sin42°的值.sinsin160.275 637 355420.669 130 606==由于计算器的型号与功能的不同,按相应的说明书使用.sin 如图,△ABC 和 △DEF都是直角三角形,它们都有一个锐角等于α,即∠D =∠A = α.在
Rt △ABC 中, ∠A的相邻的直角边(简称邻边)为AC,斜边为AB;在Rt △DEF中,∠D的邻边为DF,斜边为DE.问成立吗?∠B =90°-α=∠E ,AC 是∠B的对边,DF是∠E的对边,
依据正弦定理结论成立在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,记作 这证明了:在有一个锐角等于α的所有直角三角形中,角α的邻边与斜边的比值等于角90°-α的对边与斜边的比值.根据上述证明过程看出:对于任意锐角α,有答案:答案:3 .对于任意锐角α,都有你能说出道理吗?∵AC<AB答案:答案:答案:4.用计算器求下列锐角的正弦值和余弦值(精确到0.0001):35°68°88°9°30°18′76°18′9°38′81°53′
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
