2016-2017学年九年级数学(湘教版)上册课件:4.2正切 (共16张PPT)
文档属性
| 名称 | 2016-2017学年九年级数学(湘教版)上册课件:4.2正切 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 521.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 00:00:00 | ||
图片预览





文档简介
课件16张PPT。第4章 锐角三角函数4.2 正切【学习目标】 1、理解并掌握正切的含义,能够用tan表示直角三角形中两边的比值。
2、掌握特殊角的正切值。
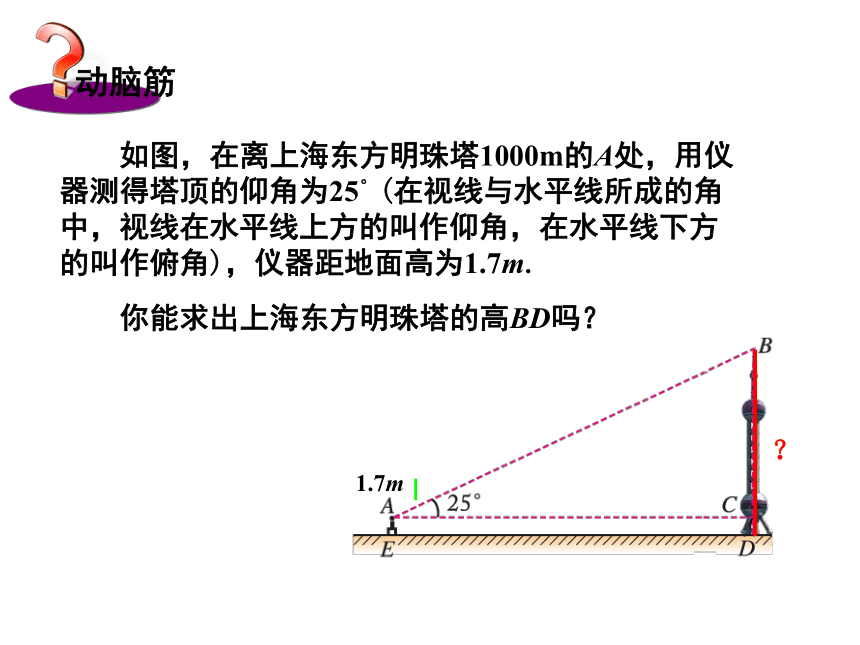
3、能够用正切进行简单的计算。 如图,在离上海东方明珠塔1000m的A处,用仪器测得塔顶的仰角为25°(在视线与水平线所成的角中,视线在水平线上方的叫作仰角,在水平线下方的叫作俯角),仪器距地面高为1.7m. 你能求出上海东方明珠塔的高BD吗? 求东方明珠塔高的关键是求三角形ABC的边长BC,因为塔高等于BC加上仪器的高1.7m.要求BC,如果已知的是
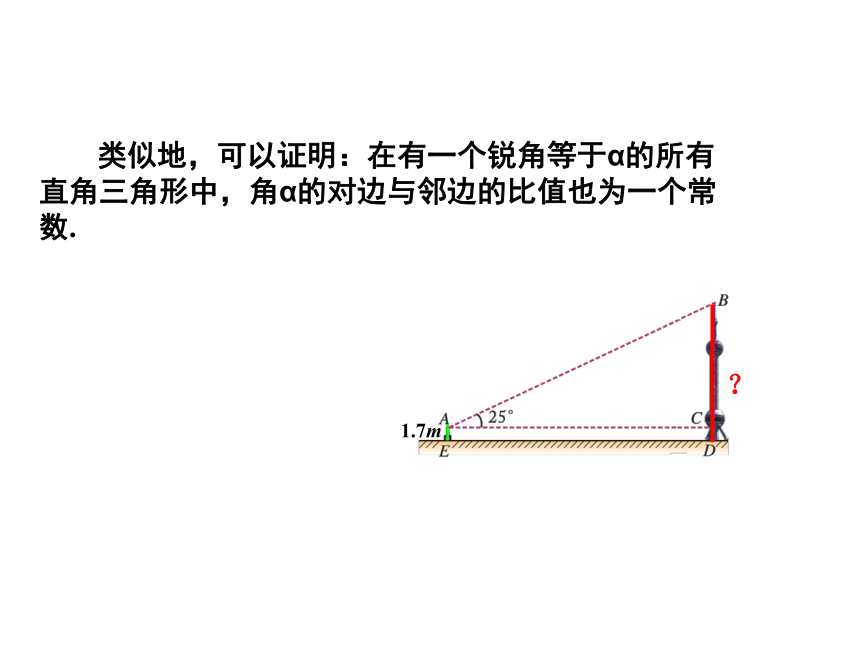
则由 可求得.而现在已知的是AC,我们能不能像探索正弦值一样来探究 的值呢? 类似地,可以证明:在有一个锐角等于α的所有直角三角形中,角α的对边与邻边的比值也为一个常数.定义 在直角三角形中,锐角α的对边与邻边的比叫作角α的正切,记作 tanα,即 从正弦、余弦、正切的定义看到,任意给定一个锐角α,都有唯一确定的比值sinα(或cosα,tanα)与它对应,因此我们把锐角的正弦、余弦和正切统称为锐角三角函数. 新知探索:30°角的三角函数值sin30°=cos30°=tan30°=cos45°=tan45°=sin45°=新知探索:45°角的三角函数值sin60°=cos60°=tan60°=新知探索:60°角的三角函数值 做一做求下列各式的值:
驶向胜利的彼岸 解: (1) (1)如图,在Rt△ABC中,∠C=90°,AC=3,tanA=2,求AB的值。 小结本节主要讲述: 正切的定义;以及会利用正切公式解决实际问题.小结本节课你有什么收获呢?
2、掌握特殊角的正切值。
3、能够用正切进行简单的计算。 如图,在离上海东方明珠塔1000m的A处,用仪器测得塔顶的仰角为25°(在视线与水平线所成的角中,视线在水平线上方的叫作仰角,在水平线下方的叫作俯角),仪器距地面高为1.7m. 你能求出上海东方明珠塔的高BD吗? 求东方明珠塔高的关键是求三角形ABC的边长BC,因为塔高等于BC加上仪器的高1.7m.要求BC,如果已知的是
则由 可求得.而现在已知的是AC,我们能不能像探索正弦值一样来探究 的值呢? 类似地,可以证明:在有一个锐角等于α的所有直角三角形中,角α的对边与邻边的比值也为一个常数.定义 在直角三角形中,锐角α的对边与邻边的比叫作角α的正切,记作 tanα,即 从正弦、余弦、正切的定义看到,任意给定一个锐角α,都有唯一确定的比值sinα(或cosα,tanα)与它对应,因此我们把锐角的正弦、余弦和正切统称为锐角三角函数. 新知探索:30°角的三角函数值sin30°=cos30°=tan30°=cos45°=tan45°=sin45°=新知探索:45°角的三角函数值sin60°=cos60°=tan60°=新知探索:60°角的三角函数值 做一做求下列各式的值:
驶向胜利的彼岸 解: (1) (1)如图,在Rt△ABC中,∠C=90°,AC=3,tanA=2,求AB的值。 小结本节主要讲述: 正切的定义;以及会利用正切公式解决实际问题.小结本节课你有什么收获呢?
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
