人教版九年级数学上册第二十二章《二次函数》复习参考课件 (共39张PPT)
文档属性
| 名称 | 人教版九年级数学上册第二十二章《二次函数》复习参考课件 (共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 487.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 14:24:09 | ||
图片预览





文档简介
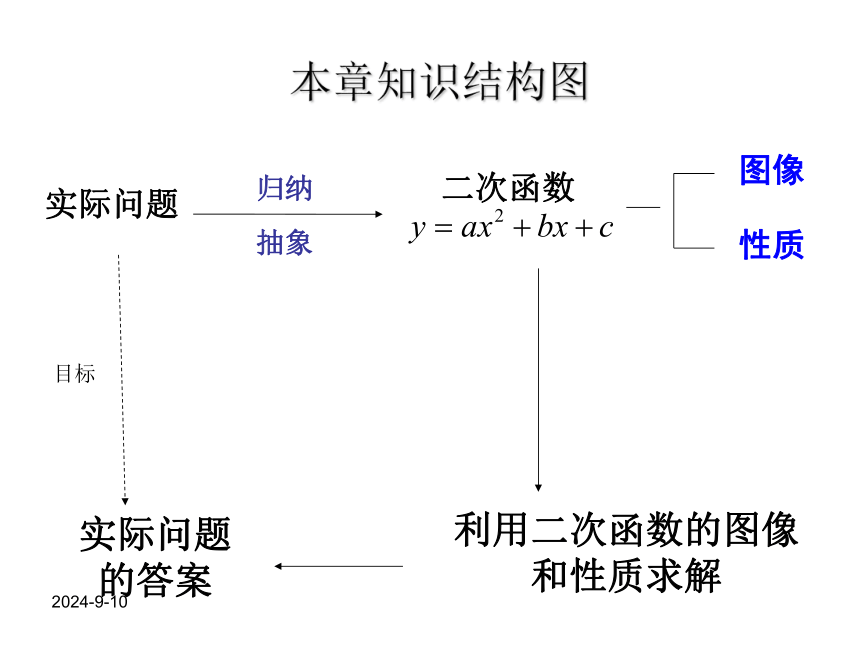
课件39张PPT。2018-10-29实际问题归纳图像实际问题
的答案本章知识结构图目标二次函数
抽象性质利用二次函数的图像
和性质求解2018-10-29一般地,如果
y=ax2+bx+c(a,b,c
是常数,a≠0),那么,y
叫做x的二次函数。一、定义二、图象特点和性质三、解析式的求法2018-10-291.特殊的二次函数
y=ax2 (a≠0)
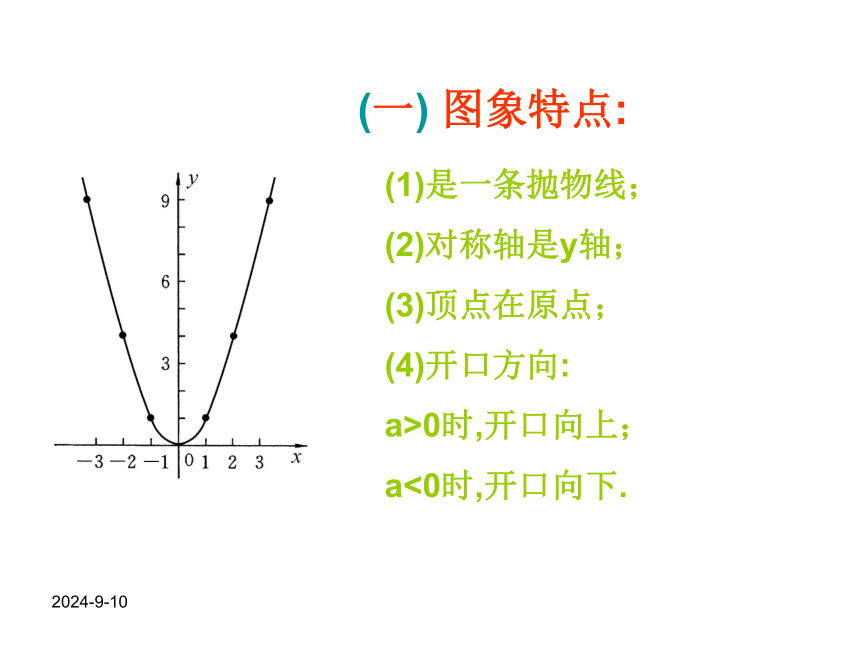
的图象特点和函数性质一、定义三、解析式的求法2018-10-29(1)是一条抛物线;
(2)对称轴是y轴;
(3)顶点在原点;
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.(一) 图象特点:2018-10-29
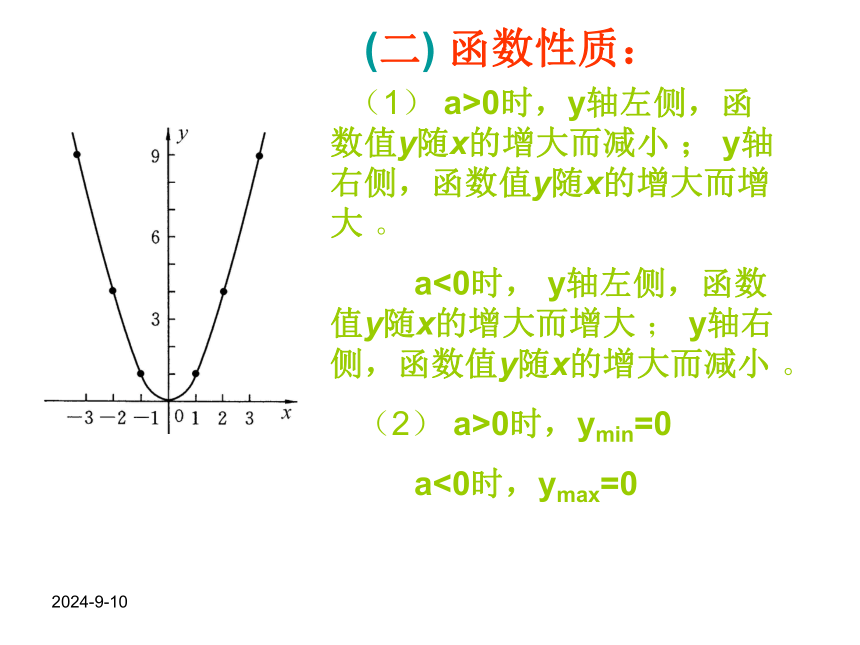
(1) a>0时,y轴左侧,函数值y随x的增大而减小 ; y轴右侧,函数值y随x的增大而增大 。
a<0时, y轴左侧,函数值y随x的增大而增大 ; y轴右侧,函数值y随x的增大而减小 。
(2) a>0时,ymin=0
a<0时,ymax=0
(二) 函数性质:2018-10-292.一般二次函数
y=ax2+bx+c(a≠0)
的图象特点和函数性质
一、定义三、解析式的求法2018-10-29
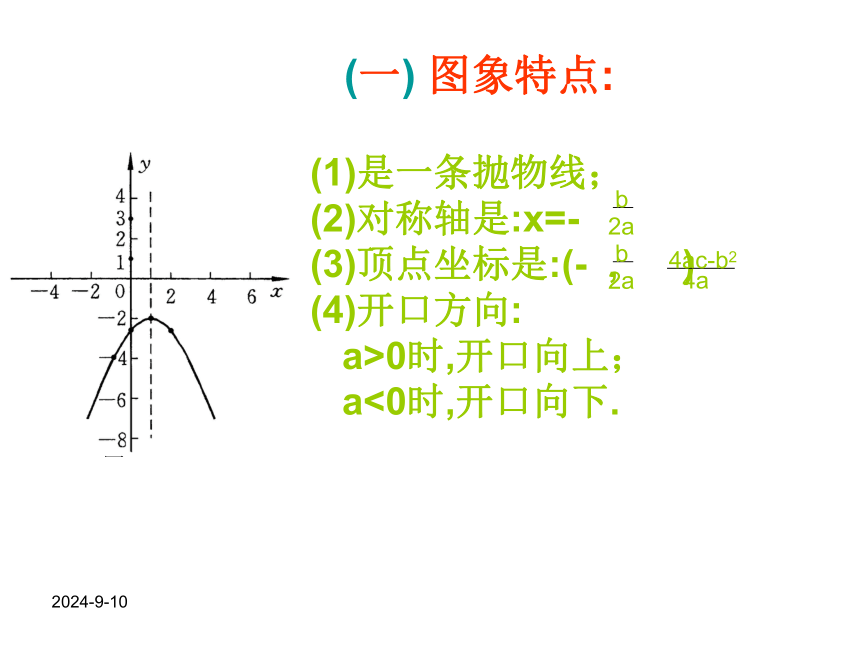
(1)是一条抛物线;
(2)对称轴是:x=-
(3)顶点坐标是:(- , )
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.
(一) 图象特点:2018-10-29
(1) a>0时,对称轴左侧(x<- ),函数值y随x的增大而减小 ;对称轴右侧(x>- ),函数值y随x的增大而增大 。
a<0时,对称轴左侧(x<- ),函数值y随x的增大而增大 ;对称轴右侧(x>- ),函数值y随x的增大而减小 。
(2) a>0时,ymin=
a<0时,ymax=
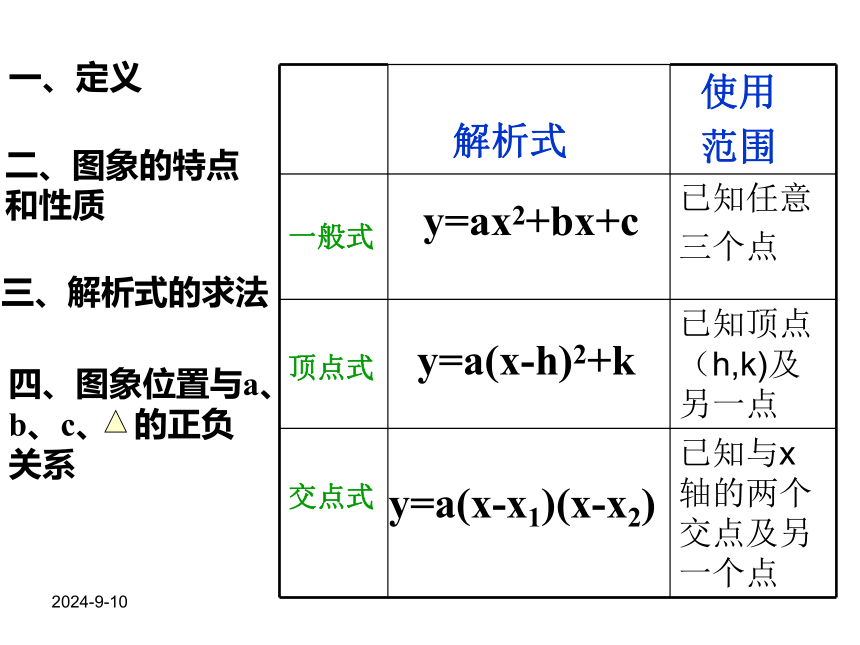
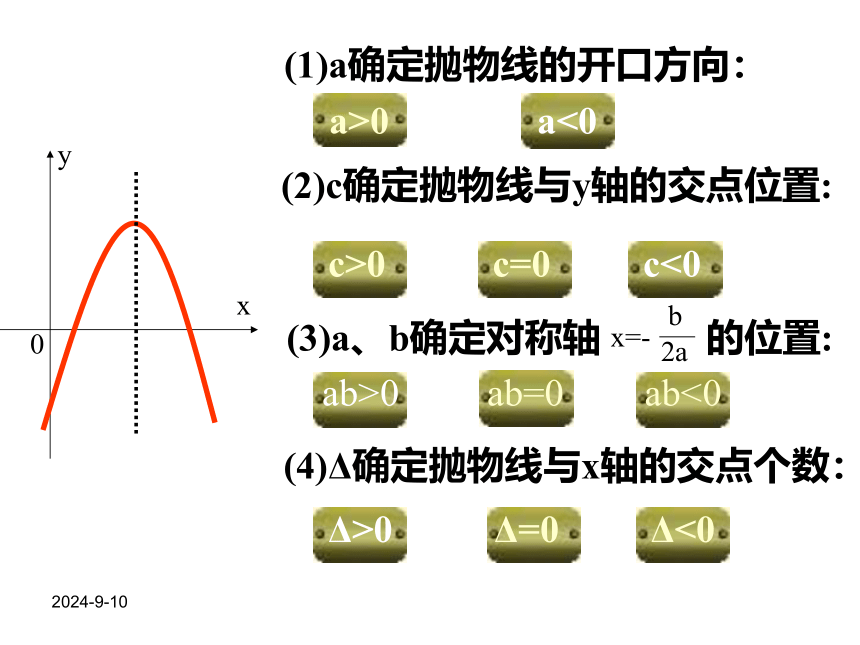
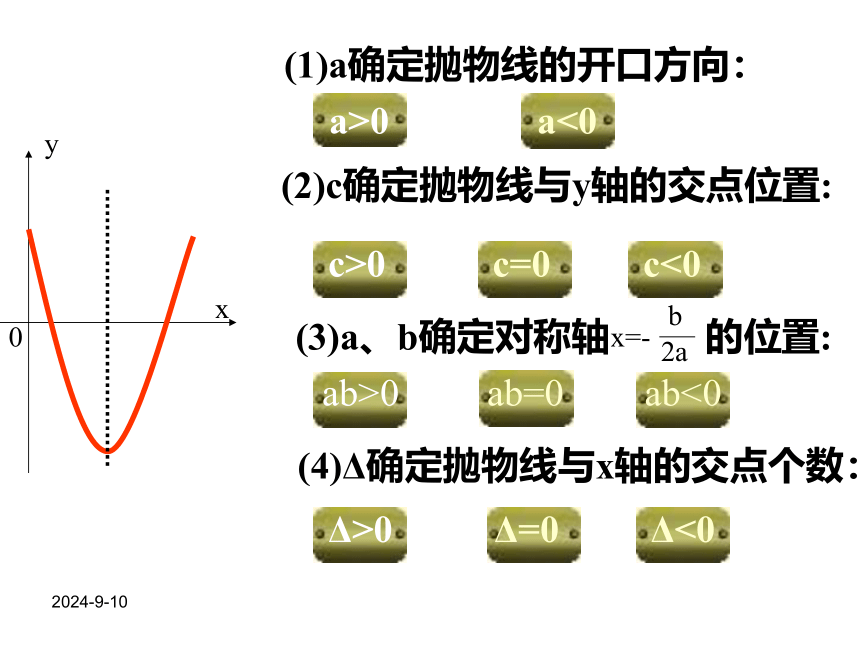
(二) 函数性质:2018-10-29y=ax2+bx+cy=a(x-h)2+ky=a(x-x1)(x-x2)一、定义二、图象的特点和性质三、解析式的求法2018-10-29xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:2018-10-29(3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置:2018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(0,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数: xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:?(x1,0)?(x2,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(x,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29题型分析:
(一)抛物线与x轴、y轴的交点急所构成的面积
例1:填空:
(1)抛物线y=x2-3x+2与y轴的交点坐标是____________,与x轴的交点坐标是____________;
(2)抛物线y=-2x2+5x-3与y轴的交点坐标是____________,与x轴的交点坐标是____________. (0,2)(1,0)和(2,0)(0,-3)2018-10-29例2:已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。2018-10-29 例3:在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
(二)根据函数性质判定函数图象之间的位置关系答案: B2018-10-29 例4、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x(三)根据函数性质求函数解析式2018-10-29例5: 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?(四)二次函数综合应用2018-10-29例5: 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?2018-10-29例5: 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?解:2018-10-29解0xy(3)2018-10-29解0?M(-1,-2)??C(0,-–)??A(-3,0)B(1,0)3 2yxD2018-10-29解解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(5)?(-1,-2)当x=-1时,y有最小值为
y最小值=-2
当x≤-1时,y随x的增大
而减小;2018-10-29解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知(6)2018-10-29巩固练习:1、填空:
(1)二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。
(2)抛物线y=-2x2+4x与x轴的交点坐标是___________
(3)已知函数y=—x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________
(4)二次函数y=mx2-3x+2m-m2的图象经过原点,则m= ____。12(0,0)(2,0)x<122018-10-292.选择
抛物线y=x2-4x+3的对称轴是_____________.
A 直线x=1 B直线x= -1 C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1的________________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
(3)若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),
则对称轴是_______
A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a ? 0)与轴交于点A(2,m), B(4,m),
则对称轴是_______
A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
cBCA2018-10-293、解答题:
已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。 (1)求此二次函数的解析式; (2)设此二次函数的图象与x轴交于A,B两点,O为坐标原点,求线段OA,OB的长度之和。2018-10-29能力训练 1、 二次函数的图象如图所示,则在下列各不等式
中成立的个数是____________1-10xy①abc<0
②a+b+c < 0
③a+c > b
④2a+b=0
⑤Δ=b-4ac > 0
2018-10-292、已知二次函数y=ax2-5x+c的图象如图。(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。(3)、求它的解析式和顶点坐标;2018-10-293、已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8)。
(1)求这个二次函数的解析式;
(2)写出它的对称轴和顶点坐标。
2018-10-29归纳小结: (1)二次函数y=ax2+bx+c及抛物线的性质和应用
注意:图象的递增性,以及利用图象求自变量x或函
数值y的取值范围2018-10-29
的答案本章知识结构图目标二次函数
抽象性质利用二次函数的图像
和性质求解2018-10-29一般地,如果
y=ax2+bx+c(a,b,c
是常数,a≠0),那么,y
叫做x的二次函数。一、定义二、图象特点和性质三、解析式的求法2018-10-291.特殊的二次函数
y=ax2 (a≠0)
的图象特点和函数性质一、定义三、解析式的求法2018-10-29(1)是一条抛物线;
(2)对称轴是y轴;
(3)顶点在原点;
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.(一) 图象特点:2018-10-29
(1) a>0时,y轴左侧,函数值y随x的增大而减小 ; y轴右侧,函数值y随x的增大而增大 。
a<0时, y轴左侧,函数值y随x的增大而增大 ; y轴右侧,函数值y随x的增大而减小 。
(2) a>0时,ymin=0
a<0时,ymax=0
(二) 函数性质:2018-10-292.一般二次函数
y=ax2+bx+c(a≠0)
的图象特点和函数性质
一、定义三、解析式的求法2018-10-29
(1)是一条抛物线;
(2)对称轴是:x=-
(3)顶点坐标是:(- , )
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.
(一) 图象特点:2018-10-29
(1) a>0时,对称轴左侧(x<- ),函数值y随x的增大而减小 ;对称轴右侧(x>- ),函数值y随x的增大而增大 。
a<0时,对称轴左侧(x<- ),函数值y随x的增大而增大 ;对称轴右侧(x>- ),函数值y随x的增大而减小 。
(2) a>0时,ymin=
a<0时,ymax=
(二) 函数性质:2018-10-29y=ax2+bx+cy=a(x-h)2+ky=a(x-x1)(x-x2)一、定义二、图象的特点和性质三、解析式的求法2018-10-29xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:2018-10-29(3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置:2018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(0,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数: xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:?(x1,0)?(x2,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?(x,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29 (1)a确定抛物线的开口方向: (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数:xy0?a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<02018-10-29题型分析:
(一)抛物线与x轴、y轴的交点急所构成的面积
例1:填空:
(1)抛物线y=x2-3x+2与y轴的交点坐标是____________,与x轴的交点坐标是____________;
(2)抛物线y=-2x2+5x-3与y轴的交点坐标是____________,与x轴的交点坐标是____________. (0,2)(1,0)和(2,0)(0,-3)2018-10-29例2:已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。2018-10-29 例3:在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
(二)根据函数性质判定函数图象之间的位置关系答案: B2018-10-29 例4、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x(三)根据函数性质求函数解析式2018-10-29例5: 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?(四)二次函数综合应用2018-10-29例5: 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?2018-10-29例5: 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?解:2018-10-29解0xy(3)2018-10-29解0?M(-1,-2)??C(0,-–)??A(-3,0)B(1,0)3 2yxD2018-10-29解解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(5)?(-1,-2)当x=-1时,y有最小值为
y最小值=-2
当x≤-1时,y随x的增大
而减小;2018-10-29解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知(6)2018-10-29巩固练习:1、填空:
(1)二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。
(2)抛物线y=-2x2+4x与x轴的交点坐标是___________
(3)已知函数y=—x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________
(4)二次函数y=mx2-3x+2m-m2的图象经过原点,则m= ____。12(0,0)(2,0)x<122018-10-292.选择
抛物线y=x2-4x+3的对称轴是_____________.
A 直线x=1 B直线x= -1 C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1的________________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
(3)若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),
则对称轴是_______
A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a ? 0)与轴交于点A(2,m), B(4,m),
则对称轴是_______
A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
cBCA2018-10-293、解答题:
已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。 (1)求此二次函数的解析式; (2)设此二次函数的图象与x轴交于A,B两点,O为坐标原点,求线段OA,OB的长度之和。2018-10-29能力训练 1、 二次函数的图象如图所示,则在下列各不等式
中成立的个数是____________1-10xy①abc<0
②a+b+c < 0
③a+c > b
④2a+b=0
⑤Δ=b-4ac > 0
2018-10-292、已知二次函数y=ax2-5x+c的图象如图。(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。(3)、求它的解析式和顶点坐标;2018-10-293、已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8)。
(1)求这个二次函数的解析式;
(2)写出它的对称轴和顶点坐标。
2018-10-29归纳小结: (1)二次函数y=ax2+bx+c及抛物线的性质和应用
注意:图象的递增性,以及利用图象求自变量x或函
数值y的取值范围2018-10-29
同课章节目录
