湘教版数学八年级上第2章三角形单元复习与小结(含答案)
文档属性
| 名称 | 湘教版数学八年级上第2章三角形单元复习与小结(含答案) | 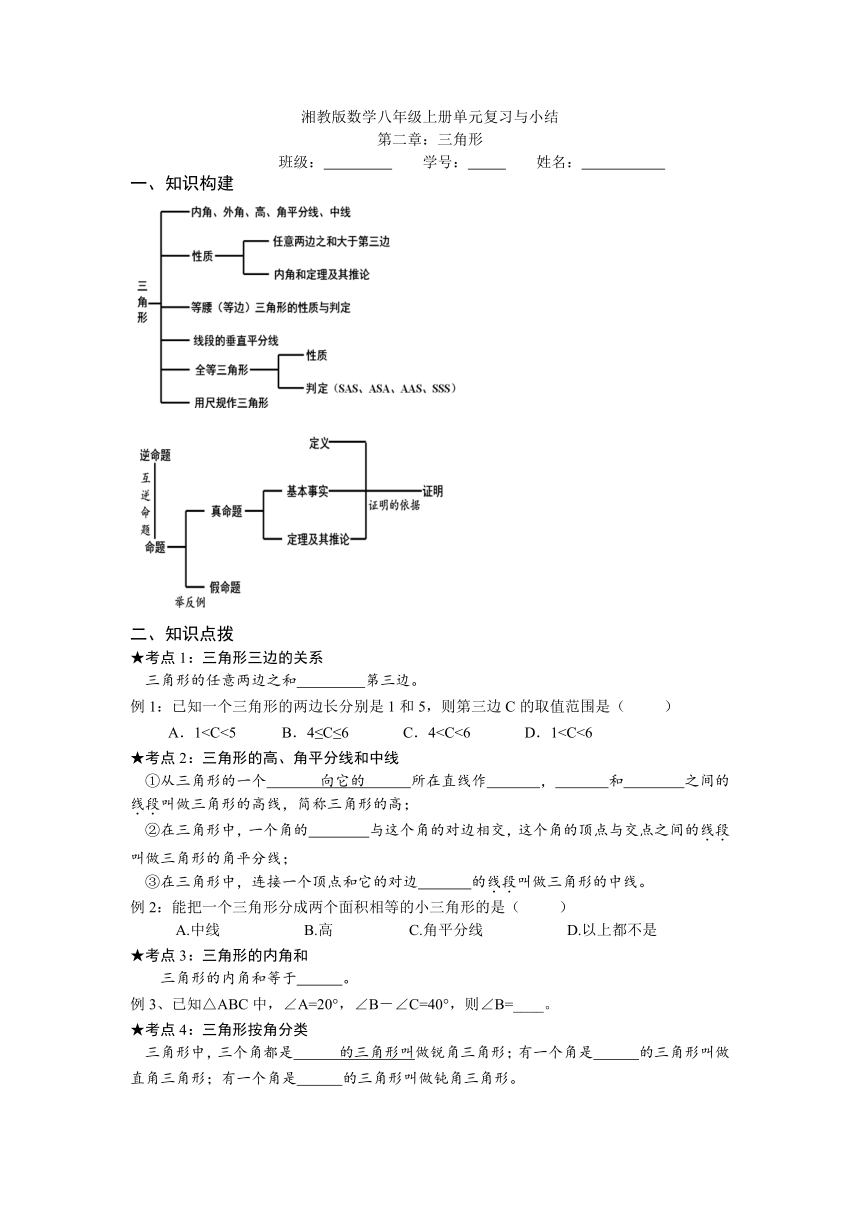 | |
| 格式 | zip | ||
| 文件大小 | 129.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 21:30:50 | ||
图片预览



文档简介
湘教版数学八年级上册单元复习与小结
第二章:三角形
班级:
学号:
姓名:
一、知识构建
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
二、知识点拨
★考点1:三角形三边的关系
三角形的任意两边之和
第三边。
例1:已知一个三角形的两边长分别是1和5,则第三边C的取值范围是(
)
A.1B.4≤C≤6
C.4D.1★考点2:三角形的高、角平分线和中线
①从三角形的一个
向它的
( http: / / www.21cnjy.com )
所在直线作
,
和
之间的线段叫做三角形的高线,简称三角形的高;
②在三角形中,一个角的
与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线;
③在三角形中,连接一个顶点和它的对边
的线段叫做三角形的中线。
例2:能把一个三角形分成两个面积相等的小三角形的是(
)
A.中线
B.高
C.角平分线
D.以上都不是
★考点3:三角形的内角和
三角形的内角和等于
。
例3、已知△ABC中,∠A=20°,∠B-∠C=40°,则∠B=____。
★考点4:三角形按角分类
三角形中,三个角都是
的三角形叫
( http: / / www.21cnjy.com )做锐角三角形;有一个角是
的三角形叫做直角三角形;有一个角是
的三角形叫做钝角三角形。
例4:满足下列条件的△ABC是锐角三角形、直角三角形还是钝角三角形?
(1)∠A=20°,∠B
=65°,则△ABC是
;(2)
,则△ABC是
(3)∠A:∠B:∠C=2:3:4,则△ABC是
★考点5:三角形的外角
①定义:三角形的一边与另一边的
所组成的角叫做三角形的外角;
②性质:三角形的一个外角等于
。
例5:在△ABC中,∠A的外角是80°,则∠B+∠C=(
)
A.100°
B.80°
C.60°
D.40°
★考点6:命题与逆命题
①一般地,对某一件事情做出
的语句(陈述句)叫做命题,命题常写成“如果……,那么……”的形式,其中“如果”引出的部分是
,“那么”引出的部分是
;
②对于两个命题,如果一个命
( http: / / www.21cnjy.com )题的条件和结论分别是另一个命题的
,那么这两个命题称为
,其中一个叫做
,另一个叫做
。
例6:下列语句是命题的是(
)
(1)两点之间,线段最短;
(2)请画出两条互相平行的直线;
(3)过直线外一点作已知直线的垂线;(4)如果两个角的和是90度,那么这两个角互余.
A.(2)(3)
B.(3)(4)
C.(1)(2)
D.(1)(4)
★考点7:真命题与假命题
正确地命题叫做
,错误的命题叫做
。
例7、下列命题中,属于假命题的是(
)
A.若a-b=0,则a=b=0
B.若a-b>0,则a>b
C.若a-b<0,则a<b
D.若a-b≠0,则a≠b
★考点8:等腰三角形的性质
定义:
的三角形叫做等腰三角形;
①对称性:等腰三角形是
图形,对称轴是
;
②“三线合一”:等腰三角形
上的高、中线及
的角平分线重合;
③“等边对等角”:等腰三角形的两
相等。
例8:等腰三角形的两边长为25cm和1
( http: / / www.21cnjy.com )2cm,
那么它的第三条边长为______;等腰三角形的一个外角是70°,则其底角等于
°;等腰三角形的角平分线、高线和中线的总数有
条。
★考点9:等边三角形的性质
定义:
的三角形叫做等边三角形;
①等边三角形的三个内角
,且都等于
;
②等边三角形是特殊的
三角形。
例9:等边三角形的对称轴有(
)
A.1条
B.2条
C.3条
D.4条
★考点10:等腰(等边)三角形的判定
等腰三角形的判定定理:
的三角形是等腰三角形(简称“等角对等边”);
等边三角形的判定定理:①三个角都是
的三角形是等边三角形;
②有一个角是
的
三角形是等边三角形。
例10:下列叙述不正确的是(
)
A、有两个内角是700和400的三角形是等腰三角形
B、一个外角的平分线平行于一边的三角形是等腰三角形
C、有两个内角不相等的三角形一定不是等腰三角形
D、三个外角都相等的三角形是等边三角形
★考点11:线段的垂直平分线
定义:
且
一条线段的
叫做这条线段的垂直平分线;
性质定理:线段垂直平分线上的点到线段两端的距离
;
性质定理的逆定理:到线段两端距离
的点在线段的垂直平分线上。
例11:在△ABC中,AB边的垂直平分线交AC于点E,△ABC和△BEC的周长分别是24和14,则AB=
。
★考点12:全等三角形的性质
定义:
的两个三角形叫做全等三角形;
性质:全等三角形的对应边
;全等三角形的对应角
。
例12:已知△ABC≌△DFE,∠A=25°,∠C=96°,AC=10,则∠BOD的度数是
,BD的长是
。
★考点13:全等三角形的判定
两边及其
分别相等的两个三角形全等,简写成“边角边”或“SAS”;
两角及其
分别相等的两个三角形全等,简写成“角边角”或“ASA”;
两角分别相等且其中一组等角的
相等的两个三角形全等,简写成“角角边”或“AAS”;
分别相等的两个三角形全等,简写成“边边边”或“SSS”。
三、当堂测评
一、选择题(本题共8小题,每小题4分,共32分)
1.
下面各组线段中,能组成三角形的是(
)
A.5,6,11
B.8,8,16
C.4,5,10
D.6,9,14
2.
在等腰三角形ABC中,它的两边长分别为8cm和3cm,则它的周长为(
)
A.19cm
B.19cm和14cm
C.11cm
D.10cm
3.
对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是(
)
A.∠1=50°,∠2=40°
B.∠1=50°,∠2=50°
C.∠1=∠2=45°
D.∠1=40°,∠2=40°
4.
有一个角是50°的等腰三角形其顶角的度数为(
)
A.80° B.50° C.80°或50° D.65.5°
5.
下列有关垂直平分线的说法中不正确的是(
)
A、垂直平分线是一条射线;
B、垂直平分线是一条直线
C、线段的垂直平分线是这条线段的对称轴;
D、到线段的两端点距离相等的点在它的垂直平分线上。
6.
如右图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于(
)
A.120°
B.115°
C.110°
D.105°
7.
下列条件中,不能判定△ABC≌△A′B′C′的是(
)
A、AB=A′B′,∠A=∠A′,AC=A′C′
B、AB=A′B′,∠A=∠A′,∠B=∠B′
C、AB=A′B′,∠A=∠A′,∠C=∠C′
D、∠A=∠A′,∠B=∠B′,∠C=∠C′
8.
如右图,在中,AB=AC,AD=DE,,,
则的度数为(
)
A.
B.
C.
D.
二、填空题(本题共8小题,每小题4分,共32分)
9.
已知线段AB=8㎝,直线CD是AB的垂直平分线,且AB交CD于E,则AE=
㎝,∠AEC=
°。
10.
请将“同位角相等”改写成“如果···,那么···”的形式,
11.
一个三角形三个内角度数的比是2∶3∶4,那么这个三角形是
三角形。
12.
已知等腰三角形的一个外角为150°,则它的底角为_____。
13.
等腰三角形的周长为36,
腰比底长3,
则此等腰三角形的腰长为________,底边长为________。
14.
已知AD是等边△ABC的高,BE是AC边的中线,AD与BE交于点F,则∠AFE=___
___。
15.
如左图,两平面镜α、β的夹
( http: / / www.21cnjy.com )角
θ,入射光线AO平行于β,入射到α上,经两次反射后的出射光线CB平行于α,则角θ等于________。
16.
如右图,在中,点是上一点,,,则
。
三、解答题(本题共3小题,共36分)
17.
在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,求∠AEB.
18、如图,中,,于
,平分交于,交于,求证:是等腰三角形.
19、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并
( http: / / www.21cnjy.com )给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
.
参考答案:
1.D
2.A
3.C
4.C
5.A
6.B
7.D
8.C
9.
4,90
10.如果两个角是同位角,那么这两个角相等
11.锐角
12.
75°或30°
13.
13,10
14.60°
15.60°
16.25°
17.120°
18.提示:利用等角对等边来证明
19.
⑴△ABE≌△ACD
证明:∠BAE=∠BAC+∠CAE,∠CAD=∠EAD+∠CAE,
∠BAE=∠CAD
又AB=AC,AE=AD
△ABE≌△ACD
⑵证明:∠CDE=45°-∠ADC
∠CED=45°-∠BEA
∠DCB=∠CDE+∠CED=45°-∠ADC+45°-∠BEA
∠ADC=∠BEA
∠DCB
=90°
即:DC⊥BE
第二章:三角形
班级:
学号:
姓名:
一、知识构建
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
二、知识点拨
★考点1:三角形三边的关系
三角形的任意两边之和
第三边。
例1:已知一个三角形的两边长分别是1和5,则第三边C的取值范围是(
)
A.1
C.4
①从三角形的一个
向它的
( http: / / www.21cnjy.com )
所在直线作
,
和
之间的线段叫做三角形的高线,简称三角形的高;
②在三角形中,一个角的
与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线;
③在三角形中,连接一个顶点和它的对边
的线段叫做三角形的中线。
例2:能把一个三角形分成两个面积相等的小三角形的是(
)
A.中线
B.高
C.角平分线
D.以上都不是
★考点3:三角形的内角和
三角形的内角和等于
。
例3、已知△ABC中,∠A=20°,∠B-∠C=40°,则∠B=____。
★考点4:三角形按角分类
三角形中,三个角都是
的三角形叫
( http: / / www.21cnjy.com )做锐角三角形;有一个角是
的三角形叫做直角三角形;有一个角是
的三角形叫做钝角三角形。
例4:满足下列条件的△ABC是锐角三角形、直角三角形还是钝角三角形?
(1)∠A=20°,∠B
=65°,则△ABC是
;(2)
,则△ABC是
(3)∠A:∠B:∠C=2:3:4,则△ABC是
★考点5:三角形的外角
①定义:三角形的一边与另一边的
所组成的角叫做三角形的外角;
②性质:三角形的一个外角等于
。
例5:在△ABC中,∠A的外角是80°,则∠B+∠C=(
)
A.100°
B.80°
C.60°
D.40°
★考点6:命题与逆命题
①一般地,对某一件事情做出
的语句(陈述句)叫做命题,命题常写成“如果……,那么……”的形式,其中“如果”引出的部分是
,“那么”引出的部分是
;
②对于两个命题,如果一个命
( http: / / www.21cnjy.com )题的条件和结论分别是另一个命题的
,那么这两个命题称为
,其中一个叫做
,另一个叫做
。
例6:下列语句是命题的是(
)
(1)两点之间,线段最短;
(2)请画出两条互相平行的直线;
(3)过直线外一点作已知直线的垂线;(4)如果两个角的和是90度,那么这两个角互余.
A.(2)(3)
B.(3)(4)
C.(1)(2)
D.(1)(4)
★考点7:真命题与假命题
正确地命题叫做
,错误的命题叫做
。
例7、下列命题中,属于假命题的是(
)
A.若a-b=0,则a=b=0
B.若a-b>0,则a>b
C.若a-b<0,则a<b
D.若a-b≠0,则a≠b
★考点8:等腰三角形的性质
定义:
的三角形叫做等腰三角形;
①对称性:等腰三角形是
图形,对称轴是
;
②“三线合一”:等腰三角形
上的高、中线及
的角平分线重合;
③“等边对等角”:等腰三角形的两
相等。
例8:等腰三角形的两边长为25cm和1
( http: / / www.21cnjy.com )2cm,
那么它的第三条边长为______;等腰三角形的一个外角是70°,则其底角等于
°;等腰三角形的角平分线、高线和中线的总数有
条。
★考点9:等边三角形的性质
定义:
的三角形叫做等边三角形;
①等边三角形的三个内角
,且都等于
;
②等边三角形是特殊的
三角形。
例9:等边三角形的对称轴有(
)
A.1条
B.2条
C.3条
D.4条
★考点10:等腰(等边)三角形的判定
等腰三角形的判定定理:
的三角形是等腰三角形(简称“等角对等边”);
等边三角形的判定定理:①三个角都是
的三角形是等边三角形;
②有一个角是
的
三角形是等边三角形。
例10:下列叙述不正确的是(
)
A、有两个内角是700和400的三角形是等腰三角形
B、一个外角的平分线平行于一边的三角形是等腰三角形
C、有两个内角不相等的三角形一定不是等腰三角形
D、三个外角都相等的三角形是等边三角形
★考点11:线段的垂直平分线
定义:
且
一条线段的
叫做这条线段的垂直平分线;
性质定理:线段垂直平分线上的点到线段两端的距离
;
性质定理的逆定理:到线段两端距离
的点在线段的垂直平分线上。
例11:在△ABC中,AB边的垂直平分线交AC于点E,△ABC和△BEC的周长分别是24和14,则AB=
。
★考点12:全等三角形的性质
定义:
的两个三角形叫做全等三角形;
性质:全等三角形的对应边
;全等三角形的对应角
。
例12:已知△ABC≌△DFE,∠A=25°,∠C=96°,AC=10,则∠BOD的度数是
,BD的长是
。
★考点13:全等三角形的判定
两边及其
分别相等的两个三角形全等,简写成“边角边”或“SAS”;
两角及其
分别相等的两个三角形全等,简写成“角边角”或“ASA”;
两角分别相等且其中一组等角的
相等的两个三角形全等,简写成“角角边”或“AAS”;
分别相等的两个三角形全等,简写成“边边边”或“SSS”。
三、当堂测评
一、选择题(本题共8小题,每小题4分,共32分)
1.
下面各组线段中,能组成三角形的是(
)
A.5,6,11
B.8,8,16
C.4,5,10
D.6,9,14
2.
在等腰三角形ABC中,它的两边长分别为8cm和3cm,则它的周长为(
)
A.19cm
B.19cm和14cm
C.11cm
D.10cm
3.
对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是(
)
A.∠1=50°,∠2=40°
B.∠1=50°,∠2=50°
C.∠1=∠2=45°
D.∠1=40°,∠2=40°
4.
有一个角是50°的等腰三角形其顶角的度数为(
)
A.80° B.50° C.80°或50° D.65.5°
5.
下列有关垂直平分线的说法中不正确的是(
)
A、垂直平分线是一条射线;
B、垂直平分线是一条直线
C、线段的垂直平分线是这条线段的对称轴;
D、到线段的两端点距离相等的点在它的垂直平分线上。
6.
如右图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于(
)
A.120°
B.115°
C.110°
D.105°
7.
下列条件中,不能判定△ABC≌△A′B′C′的是(
)
A、AB=A′B′,∠A=∠A′,AC=A′C′
B、AB=A′B′,∠A=∠A′,∠B=∠B′
C、AB=A′B′,∠A=∠A′,∠C=∠C′
D、∠A=∠A′,∠B=∠B′,∠C=∠C′
8.
如右图,在中,AB=AC,AD=DE,,,
则的度数为(
)
A.
B.
C.
D.
二、填空题(本题共8小题,每小题4分,共32分)
9.
已知线段AB=8㎝,直线CD是AB的垂直平分线,且AB交CD于E,则AE=
㎝,∠AEC=
°。
10.
请将“同位角相等”改写成“如果···,那么···”的形式,
11.
一个三角形三个内角度数的比是2∶3∶4,那么这个三角形是
三角形。
12.
已知等腰三角形的一个外角为150°,则它的底角为_____。
13.
等腰三角形的周长为36,
腰比底长3,
则此等腰三角形的腰长为________,底边长为________。
14.
已知AD是等边△ABC的高,BE是AC边的中线,AD与BE交于点F,则∠AFE=___
___。
15.
如左图,两平面镜α、β的夹
( http: / / www.21cnjy.com )角
θ,入射光线AO平行于β,入射到α上,经两次反射后的出射光线CB平行于α,则角θ等于________。
16.
如右图,在中,点是上一点,,,则
。
三、解答题(本题共3小题,共36分)
17.
在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,求∠AEB.
18、如图,中,,于
,平分交于,交于,求证:是等腰三角形.
19、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并
( http: / / www.21cnjy.com )给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
.
参考答案:
1.D
2.A
3.C
4.C
5.A
6.B
7.D
8.C
9.
4,90
10.如果两个角是同位角,那么这两个角相等
11.锐角
12.
75°或30°
13.
13,10
14.60°
15.60°
16.25°
17.120°
18.提示:利用等角对等边来证明
19.
⑴△ABE≌△ACD
证明:∠BAE=∠BAC+∠CAE,∠CAD=∠EAD+∠CAE,
∠BAE=∠CAD
又AB=AC,AE=AD
△ABE≌△ACD
⑵证明:∠CDE=45°-∠ADC
∠CED=45°-∠BEA
∠DCB=∠CDE+∠CED=45°-∠ADC+45°-∠BEA
∠ADC=∠BEA
∠DCB
=90°
即:DC⊥BE
同课章节目录
