江苏省徐州市睢宁县古邳中学2016-2017学年高二上学期第一次月考数学试题
文档属性
| 名称 | 江苏省徐州市睢宁县古邳中学2016-2017学年高二上学期第一次月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-11 22:44:33 | ||
图片预览



文档简介
睢宁县古邳中学2016-2017学年度第一次月考
高二年级月考数学试题
2016.10.08
一、填空题
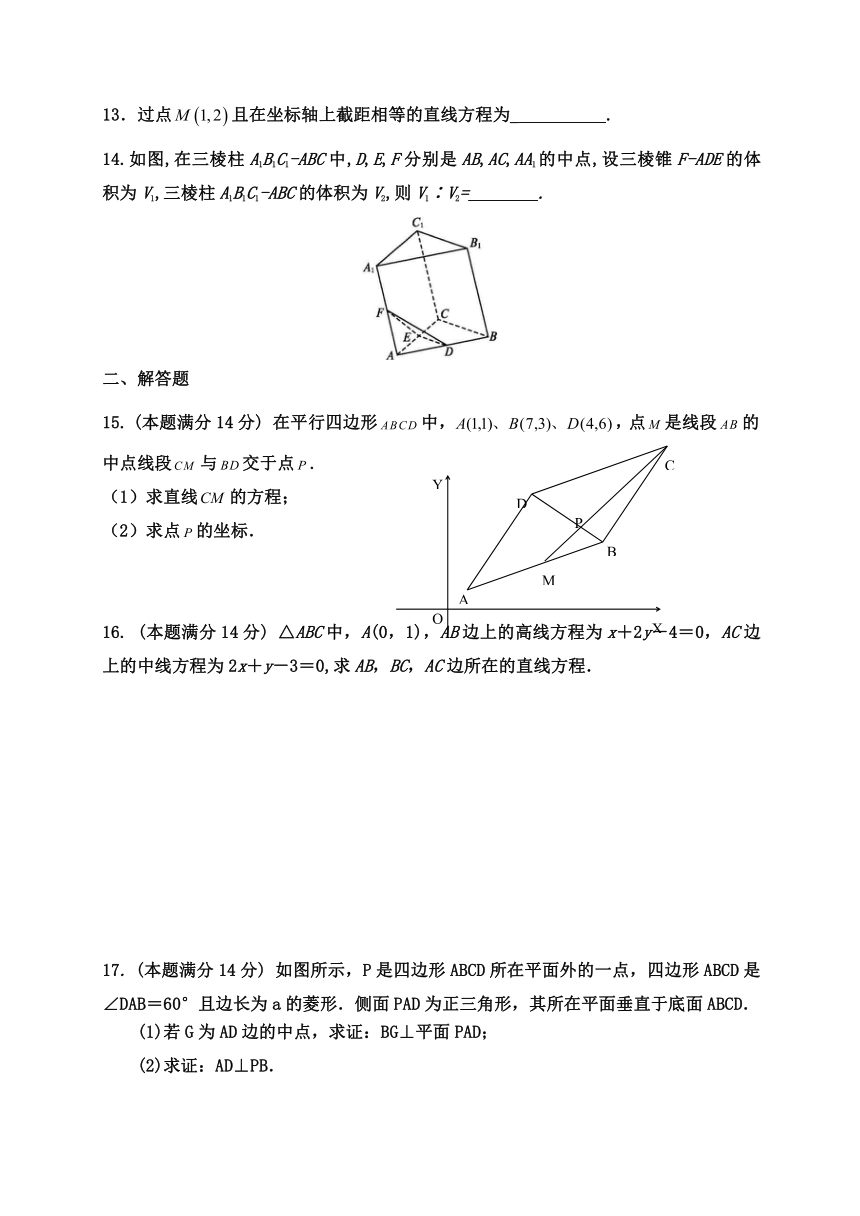
1.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为____________.
2.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为______
3.如图所示,在直四棱柱ABCD—A1B1C1D1中,当底面四边形A1B1C1D1满足条件________时,有A1C⊥B1D1(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).
4.
不同直线m、n和不同平面α、β.给出下列命题:
① m∥β;
② n∥β;
③ m,n异面;
④ m⊥β.
其中假命题的个数为________.
5.如图所示,在正方体ABCD-A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是________.(填序号)
6.α,β是两个平面,m,n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m α,那么m∥β.
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
7.
已知长方体的长、宽、高分别为,则该长方体的外接球的半径
是
cm
8.已知α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:____________.
9.
如图所示,已知PA⊥矩形ABCD所在的平面,图中互相垂直的平面有________对.
10.
若α⊥β,α∩β=l,点P∈α,PDl,则下列命题中正确的为________.(只填序号)
①过P垂直于l的平面垂直于β;
②过P垂直于l的直线垂直于β;
③过P垂直于α的直线平行于β;
④过P垂直于β的直线在α内.
11.
已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0互相平行则a的值为_____
12.
已知直线l:mx﹣y=4,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为
.
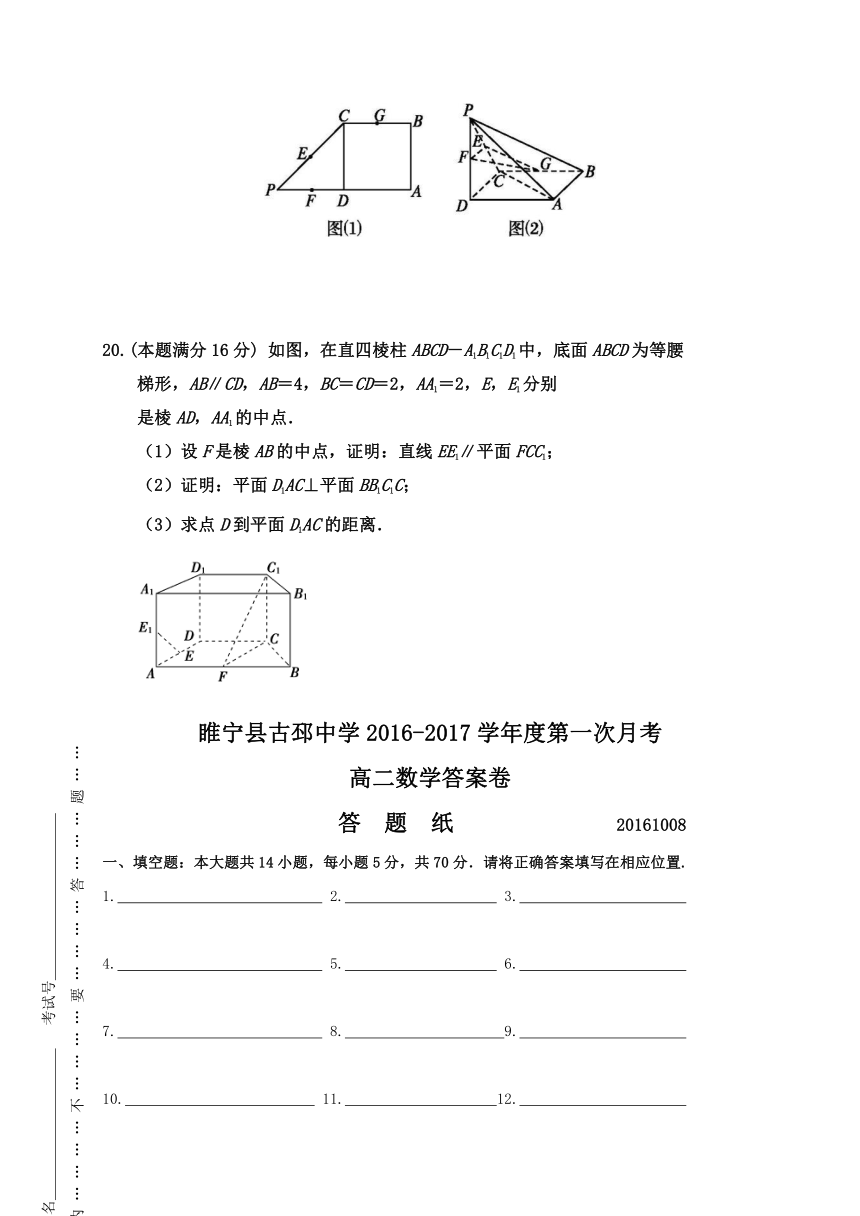
13.过点且在坐标轴上截距相等的直线方程为_
.
14.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2= .
二、解答题
15.
(本题满分14分)
在平行四边形中,,点是线段的中点线段与交于点.
(1)求直线的方程;
(2)求点的坐标.
16.
(本题满分14分)
△ABC中,A(0,1),AB边上的高线方程为x+2y-4=0,AC边上的中线方程为2x+y-3=0,求AB,BC,AC边所在的直线方程.
17.
(本题满分14分)
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
18.
(本题满分16分)如图,在直三棱柱ABC—A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C.
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
19.
(本题满分16分)
如图(1),在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
(1)求证:AP∥平面EFG;
(2)求三棱锥P-ABC的体积.
20.(本题满分16分)
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰
梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别
是棱AD,AA1的中点.
(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;
(2)证明:平面D1AC⊥平面BB1C1C;
(3)求点D到平面D1AC的距离.
睢宁县古邳中学2016-2017学年度第一次月考
高二数学答案卷
答
题
纸
20161008
一、填空题:本大题共14小题,每小题5分,共70分.请将正确答案填写在相应位置.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
二、解答题:本大题共6小题,共90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本题满分14)解:
16.(本题满分14)解:
17.(本题满分14分)解:
18.(本题满分16分)解:
19.(本题满分16分)解:19.
20.(本题满分16分)解:
高二年级第一次月考调研数学卷
参考答案
20161008
一、填空题
1.36;2.;3.B1D1⊥A1C1,还可以填写四边形A1B1C1D1是菱形,正方形等条件;
4.
3;5.①④;6.②③④;7.
;8.①③④ ②(或②③④ ①);9.
5;
10.①③④;11.-1;12.
0,2;13.2x-y=0或x+y-3=0;14.1∶24.
二、解答题
15.解:(1)解得C点坐标C(10,8)…………………………..3分
解得点M坐标(4,2)……………………………..4分
求出直线CM方程2x-3y-2=0………………………7分
(2)求出BD直线方程x+y-10=0............10分
联立方程组
…………………11分
解得x=,y=,……………………………13分
所以点P坐标为(,)…………………14分
16.解:直线AB的斜率为2,∴AB边所在的直线方程为,
直线AB与AC边中线的方程交点为
设AC边中点D(x1,3-2x1),C(4-2y1,y1),∵D为AC的中点,由中点坐标公式得
边所在的直线方程为;
AC边所在的直线方程为y=1.
17.证明
(1)连结PG,由题知△PAD为正三角形,G是AD的中点,∴PG⊥AD.
又平面PAD⊥平面ABCD,∴PG⊥平面ABCD,∴PG⊥BG.
又∵四边形ABCD是菱形且∠DAB=60°,∴BG⊥AD.
又AD∩PG=G,∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD,PG⊥AD.
所以AD⊥平面PBG,所以AD⊥PB.
18.证明 (1)由E、F分别是A1B、A1C的中点知EF∥BC.
因为EF 平面ABC.BC 平面ABC.
所以EF∥平面ABC.
(2)由三棱柱ABC—A1B1C1为直三棱柱知CC1⊥平面A1B1C1.
又A1D 平面A1B1C1,故CC1⊥A1D.
又因为A1D⊥B1C,CC1∩B1C=C,故A1D⊥平面BB1C1C,又A1D 平面A1FD,
所以平面A1FD⊥平面BB1C1C.
19.(I)证明:取AD的中点H,连接FH、GH.
∵E,F,G分别为PC、PD、CB的中点,∴EF∥CD,CGDH,
∴四边形CDHG是平行四边形,∴CD∥GH.
∴EF∥GH.∴四点EFHG四点共面.又FH∥PA.
PA 平面EFGH,FH 平面EFGH.∴PA∥平面EFGH.
(II)解:∵点P在平面ABCD上的射影为点D,∴PD⊥平面ABCD.
即PD是三棱锥P-ABC的高.
而.
∴三棱锥P-ABC的体积V=.
20.解:(1)
四边形为平行四边形
又面
,面
面…………2分
在直四棱柱中,
,
又面
,面
面…………3分
又面
面//面
又面,面…………5分
(2)
平行四边形是菱形
,易知
…………7分
在直四棱柱中,面
,面
又
面
…………9分
又面
面面…………10分
(3)易知
…………11分
设到面的距离为,则
,又
…………14分
,即到面的距离为
.
…………16分
高一(
)班
姓名
考试号
………………密……………封……………线…………内…………不…………要…………答………题……题……………………………………………………
A
X
P
Y
D
B
O
C
M
高一(
)班
姓名
考试号
………………密……………封……………线…………内…………不…………要…………答………题……题……………………………………………………
A
X
P
Y
D
B
O
C
M
---------------密--------------------------------封------------------------------------线----------------------
高二年级月考数学试题
2016.10.08
一、填空题
1.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为____________.
2.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为______
3.如图所示,在直四棱柱ABCD—A1B1C1D1中,当底面四边形A1B1C1D1满足条件________时,有A1C⊥B1D1(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).
4.
不同直线m、n和不同平面α、β.给出下列命题:
① m∥β;
② n∥β;
③ m,n异面;
④ m⊥β.
其中假命题的个数为________.
5.如图所示,在正方体ABCD-A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是________.(填序号)
6.α,β是两个平面,m,n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m α,那么m∥β.
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
7.
已知长方体的长、宽、高分别为,则该长方体的外接球的半径
是
cm
8.已知α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:____________.
9.
如图所示,已知PA⊥矩形ABCD所在的平面,图中互相垂直的平面有________对.
10.
若α⊥β,α∩β=l,点P∈α,PDl,则下列命题中正确的为________.(只填序号)
①过P垂直于l的平面垂直于β;
②过P垂直于l的直线垂直于β;
③过P垂直于α的直线平行于β;
④过P垂直于β的直线在α内.
11.
已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0互相平行则a的值为_____
12.
已知直线l:mx﹣y=4,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为
.
13.过点且在坐标轴上截距相等的直线方程为_
.
14.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2= .
二、解答题
15.
(本题满分14分)
在平行四边形中,,点是线段的中点线段与交于点.
(1)求直线的方程;
(2)求点的坐标.
16.
(本题满分14分)
△ABC中,A(0,1),AB边上的高线方程为x+2y-4=0,AC边上的中线方程为2x+y-3=0,求AB,BC,AC边所在的直线方程.
17.
(本题满分14分)
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
18.
(本题满分16分)如图,在直三棱柱ABC—A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C.
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
19.
(本题满分16分)
如图(1),在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
(1)求证:AP∥平面EFG;
(2)求三棱锥P-ABC的体积.
20.(本题满分16分)
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰
梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别
是棱AD,AA1的中点.
(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;
(2)证明:平面D1AC⊥平面BB1C1C;
(3)求点D到平面D1AC的距离.
睢宁县古邳中学2016-2017学年度第一次月考
高二数学答案卷
答
题
纸
20161008
一、填空题:本大题共14小题,每小题5分,共70分.请将正确答案填写在相应位置.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
二、解答题:本大题共6小题,共90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本题满分14)解:
16.(本题满分14)解:
17.(本题满分14分)解:
18.(本题满分16分)解:
19.(本题满分16分)解:19.
20.(本题满分16分)解:
高二年级第一次月考调研数学卷
参考答案
20161008
一、填空题
1.36;2.;3.B1D1⊥A1C1,还可以填写四边形A1B1C1D1是菱形,正方形等条件;
4.
3;5.①④;6.②③④;7.
;8.①③④ ②(或②③④ ①);9.
5;
10.①③④;11.-1;12.
0,2;13.2x-y=0或x+y-3=0;14.1∶24.
二、解答题
15.解:(1)解得C点坐标C(10,8)…………………………..3分
解得点M坐标(4,2)……………………………..4分
求出直线CM方程2x-3y-2=0………………………7分
(2)求出BD直线方程x+y-10=0............10分
联立方程组
…………………11分
解得x=,y=,……………………………13分
所以点P坐标为(,)…………………14分
16.解:直线AB的斜率为2,∴AB边所在的直线方程为,
直线AB与AC边中线的方程交点为
设AC边中点D(x1,3-2x1),C(4-2y1,y1),∵D为AC的中点,由中点坐标公式得
边所在的直线方程为;
AC边所在的直线方程为y=1.
17.证明
(1)连结PG,由题知△PAD为正三角形,G是AD的中点,∴PG⊥AD.
又平面PAD⊥平面ABCD,∴PG⊥平面ABCD,∴PG⊥BG.
又∵四边形ABCD是菱形且∠DAB=60°,∴BG⊥AD.
又AD∩PG=G,∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD,PG⊥AD.
所以AD⊥平面PBG,所以AD⊥PB.
18.证明 (1)由E、F分别是A1B、A1C的中点知EF∥BC.
因为EF 平面ABC.BC 平面ABC.
所以EF∥平面ABC.
(2)由三棱柱ABC—A1B1C1为直三棱柱知CC1⊥平面A1B1C1.
又A1D 平面A1B1C1,故CC1⊥A1D.
又因为A1D⊥B1C,CC1∩B1C=C,故A1D⊥平面BB1C1C,又A1D 平面A1FD,
所以平面A1FD⊥平面BB1C1C.
19.(I)证明:取AD的中点H,连接FH、GH.
∵E,F,G分别为PC、PD、CB的中点,∴EF∥CD,CGDH,
∴四边形CDHG是平行四边形,∴CD∥GH.
∴EF∥GH.∴四点EFHG四点共面.又FH∥PA.
PA 平面EFGH,FH 平面EFGH.∴PA∥平面EFGH.
(II)解:∵点P在平面ABCD上的射影为点D,∴PD⊥平面ABCD.
即PD是三棱锥P-ABC的高.
而.
∴三棱锥P-ABC的体积V=.
20.解:(1)
四边形为平行四边形
又面
,面
面…………2分
在直四棱柱中,
,
又面
,面
面…………3分
又面
面//面
又面,面…………5分
(2)
平行四边形是菱形
,易知
…………7分
在直四棱柱中,面
,面
又
面
…………9分
又面
面面…………10分
(3)易知
…………11分
设到面的距离为,则
,又
…………14分
,即到面的距离为
.
…………16分
高一(
)班
姓名
考试号
………………密……………封……………线…………内…………不…………要…………答………题……题……………………………………………………
A
X
P
Y
D
B
O
C
M
高一(
)班
姓名
考试号
………………密……………封……………线…………内…………不…………要…………答………题……题……………………………………………………
A
X
P
Y
D
B
O
C
M
---------------密--------------------------------封------------------------------------线----------------------
同课章节目录
