多边形内角和

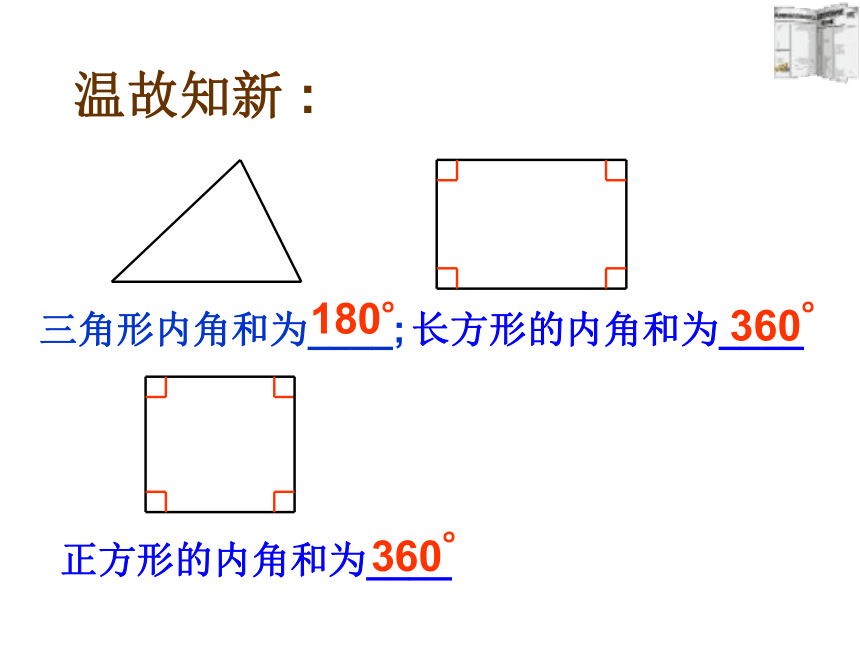
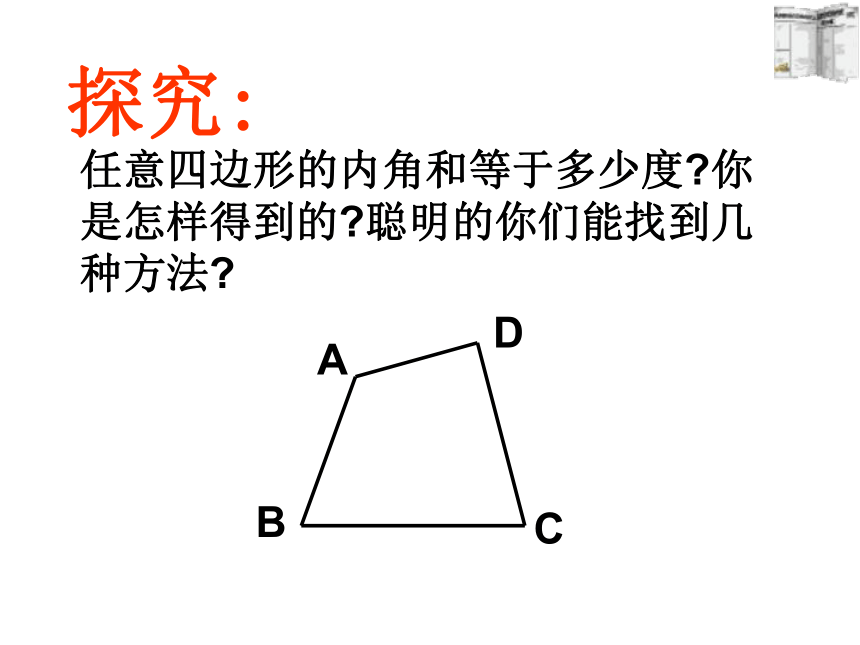
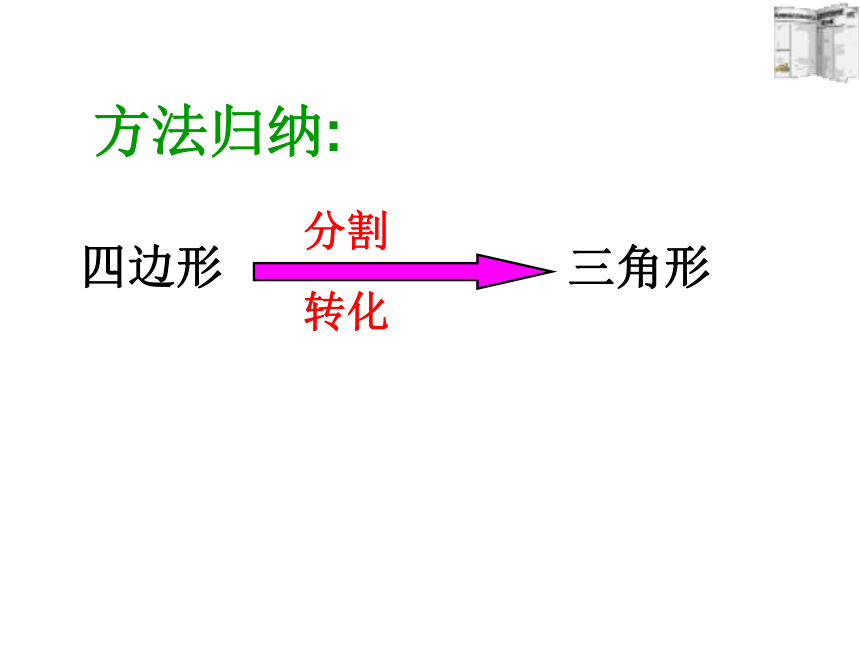
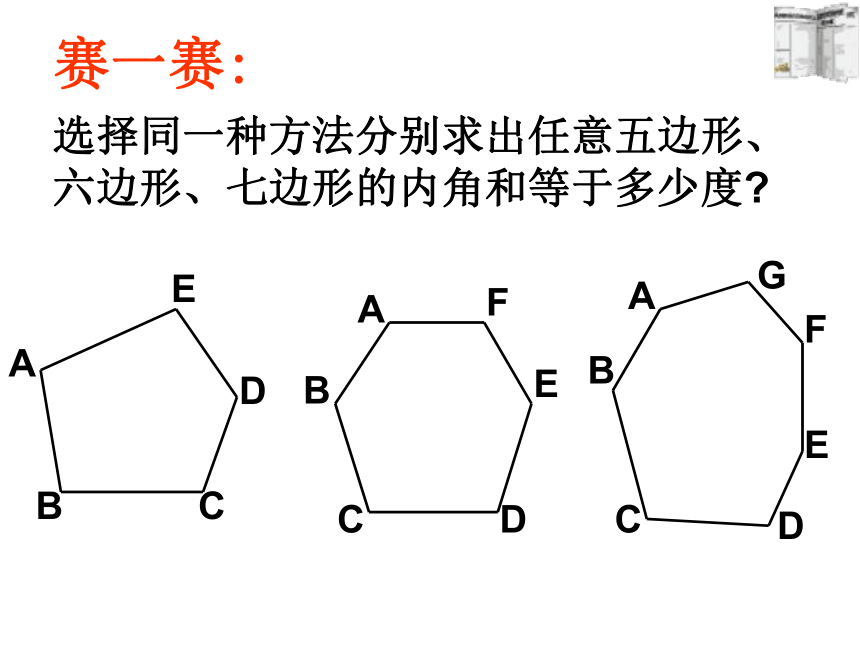
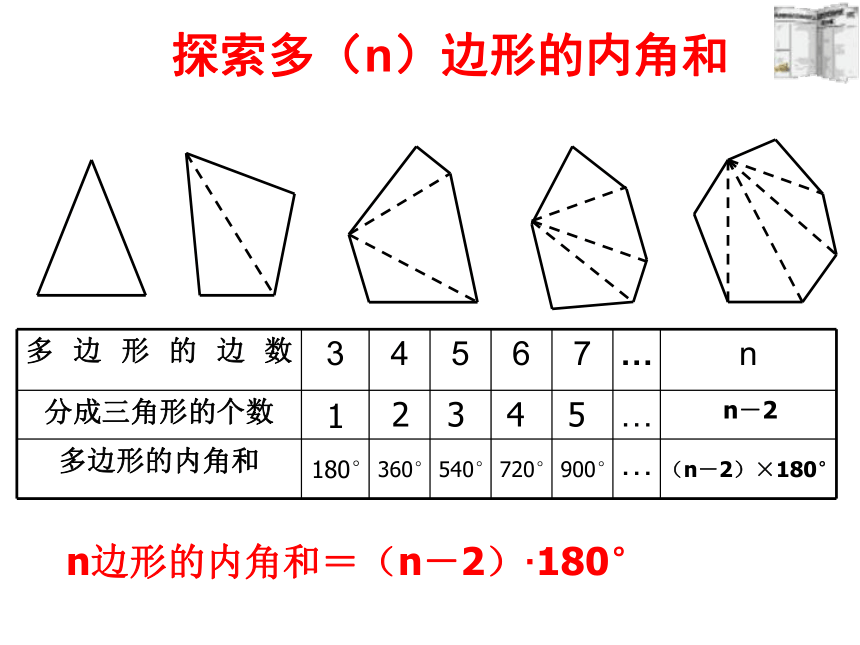
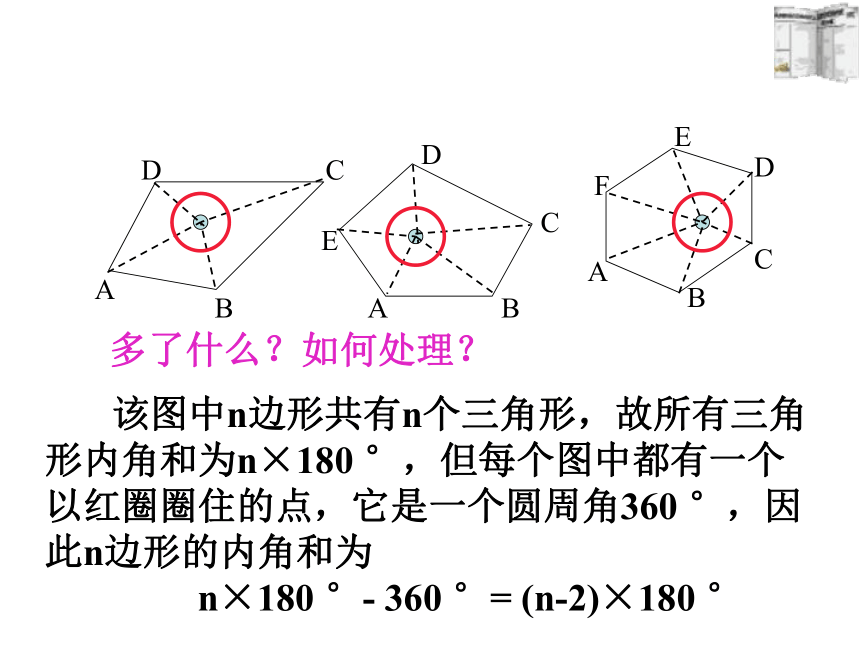
课件20张PPT。7.3.2多边形的内角和2010-04-12三角形内角和为____;长方形的内角和为____正方形的内角和为____温故知新 :探究:任意四边形的内角和等于多少度?你是怎样得到的?聪明的你们能找到几种方法?方法归纳:四边形三角形分割转化赛一赛:选择同一种方法分别求出任意五边形、六边形、七边形的内角和等于多少度?1180° 2345360° 540° 720° 900° n－2 （n－2）×180° n边形的内角和＝（n－2）·180° 探索多（n）边形的内角和 多了什么？如何处理？ 这种分割方式，将多边形分成n-1个三角形，故所有三角形的内角和为（n-1）×180 °，边上一点周围所形成的平角不是多边形的内角，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 ° 该图中n边形共有n个三角形，故所有三角形内角和为n×180 °，但每个图中都有一个以红圈圈住的点，它是一个圆周角360 °，因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °多了什么？如何处理？定理：
n边形的内角和等于(n－2)·180?.
说明：
(1)多边形的内角和仅与边数有关，与多边形的大小、形状无关；
(2)强调凸多边形的内角?的范围：0?例1：求六边形的内角和的度数。 解：（n－2）×180°＝（6－2）×180°
＝720°
答：六边形的内角和为720°。 例题分析：例2：一个正多边形的一个内角为150°，你知道它是几边形吗？ 解：设这个多边形为n边形，根据题意得：
　　　　（n－2）×180＝1５0n
　　 　　 　 n＝12
答：这个多边形是十二边形。1、 八边形的内角和等于多少 度？十边形呢？2、若一个多边形的内角和为1260°，此多边形为几边形？3、四边形的四个内角的比是8:6:3:7,求它的四个内角.他每跑完一圈，身体转过的角度之和是多少？问题1：ABCDE12345在上图中，你能求出
1+∠2+∠3+∠4+∠5的大小吗？
你是怎样得到的？ 探索:分别求出下列多边形的外角和的度数.360° 360° 360° 360° 360° 猜想与说理:n边形的外角和是多少度呢? 答:都是360°.因为多边形的外角与它相邻的内角是邻补角，所以n边形的外角和加内角和等于n·180°，内角和为(n－2)·180°,因此，外角和为：n·180°－(n－2)·180°= 360°. 结论:多边形的外角和都等于360°. 1、一个十边形的每一个内角都相等，那么这个十边形的每一个外角都等于( )
A、144° B、 72 ° C、 36° D 、18°CC巩固练习：2、一个多边形每一个外角都等于45°，则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°3、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数.有一张长方形的桌面，它的四个内角和为360°,现在锯掉它的一个角，剩下残余桌面所有的内角和是多少？有几种情况？

课后思考 小明在计算某个多边形的内角和时，由于粗心他漏掉一个内角，求得的内角和1680° ，你能否求得正确结果呢？小结： 我们通过把多边形划分为若干个三角形，用三角形内角和去求多边形内角和，从而得到多边形的内角和公式为（ｎ－２）× 180°。这种化未知为已知的转化方法，必须在学习中逐渐掌握。由于多边形外角和为360°，与边数无关，所以常把多边形内角和的问题转化为外角和来处理。